快速幂相较于普通的幂,具有占用空间少,效率更高等优点,全面碾压普通的幂。
在计算量较小时,二者相差无几,但数据规模一旦上来了,差距也就出来了。
所以,我们重点讲解快速幂
首先给出一个问题
给定 a,b,p 求a^b%p的值? ? ? ? ? 1<a,b,p<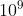
方法一(朴素):
讲道理,我们先把普通的朴素代码展示出来。从简单入手:
#include<cstdio>
unsigned long long a,b,p,x=1;
int main(){
scanf("%llu %llu %llu",&a,&b,&p);
for(int i=1;i<=b;i++){
x=x*a%p;
}
printf("%llu",x);
return 0;
}能看懂吧!有人会问那最后的答案为什么会是x,那是因为我们在计算a^b时已经插入了取模运算,如下:
(a^b)mod p
=(a*a*a*a.....*a*a*a*a) mod p
=a mod p * a mod p * a mod p * a mod p ....... * a mod p
(一个无限套娃)
我们这样做的目的,就是避免大数相乘溢出数据范围,减少计算量。
但即使这样,如果a,p足够大,相乘起来也依然能够超过unsigned long long 的数据范围
(补充: unsigned long long 的数据范围是 [0,2^64),右边是开区间!2^64约为10^9)
方法二(位运算):
先上代码:
#include<cstdio>
unsigned long long a,b,p,ans=1;
int main(){
scanf("%llu %llu %llu",&a,&b,&p);
for(;b>0;b>>=1){
if((b & 1)==1){
ans=ans*a%p;
}
a=(a*a)%p;
}
printf("%llu",ans);
return 0;
} 这个算法解释如下:
1.首先我们要明白任何一个正整数都能拆分成2的不同次幂相加的和。
例如: 7=2^0+2^1+2^2? ? ? ? ? ? ?19=2^0+2^1+2^4
说白了,就是能转换成2进制?
7? ? ?二进制? ? ? 111? ? ? ? ? ? ? 19? ? ? ? 二进制? ? ? 10011
同样对于b,我们能转化成
b=*c1+
*c2+
*c3.........的形式,很明显,cX只能为0,1,因为二进制每一位上最大为1
那么 a^b=a^(*c1+
*c2+
*c3........)
=a^?*c1? ? ?*? ? ? a^
*c2? ? *? ? ? a^??
*c3.........
=? ? ? *?
? ? ?*??
.....................
mod p
=? mod p? ? *?
? mod p? ?*??
? ?mod p....................
到这里已经可以看出
a a^2 a^3? a^n可以通过前面 a^n-1推来
只需判断b对应二进制该位上是否为1
若为1,则计算,若为0不用管,因为 2^0=1 1对乘法运算没有影响
更多的,还需要读者多多思考,注重实践
新年到来之际,祝大家新年快乐!
谢谢大家的支持!