[数据结构与算法]第二章 k-近邻算法

第二章 k-近邻算法

2.1 k-近邻算法概述

原理：

• k-近邻算法采用测量不同特征值之间的距离方法进行分类
• 存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们只选择样本数据集中前k个最相似的数据，这就是k-近邻算法中k的出处，通常k是不大于20的整数（一般为奇数）。最后，选择k个最相似数据中出现次数最多的分类，作为新数据的分类。

示例：通过电影中的镜头出现次数判断电影的种类

①首先计算未知电影与样本集中其他电影的距离

②当得到样本集中所有电影与未知电影的距离，安装距离递增排序，可以找到k个距离最近的电影

③假定k=3，k-近邻算法按照距离最近的三部电影的类型，决定未知电影的类型，而这三部电影全是爱情片，因此我们判定未知电影是爱情片

优缺点：

• 优点：精度高、对异常值不敏感、无数据输入假定
• 缺点：计算复杂度高、空间复杂度高
• 使用数据范围：数值型和标称型

k-近邻算法的一般步骤

1. 收集数据：可以使用任何方法
2. 准备数据：距离计算所需要的数值，最好是结构化的数据格式
3. 分析数据：可以使用任何方法
4. 训练算法：此步骤不适用k-近邻算法
5. 测试算法：计算错误率
6. 使用算法：首先需要输入样本数据和结构化的输出结果，然后运行k-近邻算法判定输入数据分别属于哪个分类，最后应用对计算出的分类执行后续的处理

2.1.1 准备：使用Python导入数据

import numpy as np
import operator
import matplotlib.pyplot as plt

"""
函数说明：创建数据集和标签

"""
def createDataSet():
    #group包含了四组数据
    group = np.array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    #labels包含的元素个数等于group矩阵行数
    labels = ['A','A','B','B']
    return group,labels

group,labels = createDataSet()
print(group)
print(labels)

plt.scatter(x=group[:,0],y=group[:,1])
plt.show()

2.1.2 从文本文件中解析数据

使用k-近邻算法将每组数据划分到某个类中：

对未知类别属性的数据集中的每个点依次执行以下操作：

1. 计算已知类别数据集中的点与当前点之间的距离
2. 按照距离递增次序排序
3. 选取与当前点距离最小的k个点
4. 确定前k个点所在类别的出现频率
5. 返回前k个点出现频率最高的类别作为当前点的预测分类

import numpy as np
import operator
import matplotlib.pyplot as plt

"""
函数说明：创建数据集和标签

"""
def createDataSet():
    #group包含了四组数据
    group = np.array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    #labels包含的元素个数等于group矩阵行数
    labels = ['A','A','B','B']
    return group,labels

"""
函数说明：分类器

Parameters:
    inX-用于分类的输入向量（要对其进行分类的向量）
    dataSet-输入的训练样本集
    labels-标签向量，标签向量的元素数目和矩阵dataSet的行数相同
    k-用于选择最近邻居的数据
"""
def classify0(inX,dataSet,labels,k):
    #获取训练样本集的行数
    dataSetSize = dataSet.shape[0]
    #对输入向量进行复制，使其格式与dataSet相同，之后两个矩阵相减
    diffMat = np.tile(inX,(dataSetSize,1))-dataSet
    #对矩阵中的每个值进行乘方
    sqDiffMat = diffMat**2
    #sum就是求和，axis表示沿着axis方向求和
    #axis=1按行的方向相加，返回每行的值
    #axis=0按列的方向相加，返回每列的值
    sqDistances = sqDiffMat.sum(axis=1)
    #开根号后得到距离
    distances = sqDistances**0.5
    #numpy.argsort() 函数返回的是数组值从小到大的索引值。
    sortedDistIndicies = distances.argsort()
    #创建一个字典用于保存标签及其出现的次数
    classCount = {}
    for i in range(k):
        #将距离从小到大进行排序，并取得对应的标签
        voteIlabel = labels[sortedDistIndicies[i]]
        #统计对应标签出现的次数
        classCount[voteIlabel] = classCount.get(voteIlabel,0)+1
    #operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为一些序号。
    #参数为1表示对标签出现的次数进行排序，并且是从大到小排序
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    #获得对应的标签
    return sortedClassCount[0][0]

if __name__=="__main__":
    group,labels = createDataSet()
    result = classify0([1,1.2],group,labels,3)
    print(result)

2.1.3 如何测试分类器

• 为了测试分类器的效果，我们可以使用已知答案的数据，当然答案不能告诉分类器，检验分类器给出的结果是否符合预期结果。
• 通过大量的测试数据，我们可以得到分类器的错误率——分类器给出错误结果的次数除以测试执行的总数。
• 错误率是常用的评估方法，主要用于评估分类器在某个数据集上的执行效果。完美分类器的错误率为0，最差分类器的错误率是1。

2.1.4 其他的距离公式

①欧式距离

欧几里得度量(educlidean metric)，指在m维空间中两点之间的真实距离，或者向量的自然长度，即该点到原点的距离。

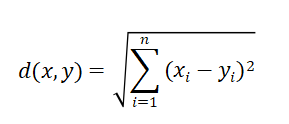
import numpy as np
from scipy.spatial.distance import pdist

x = np.array([1,2])
y = np.array([0,1])
dist = np.sqrt(np.sum(np.square(x-y)))
print(dist)

dist2 = pdist(np.vstack([x,y]))
print(dist2)

②曼哈顿距离

Manhattan Distance，也称为城市街区距离（City Block distance）。如果把欧式距离理解成点到点的直线距离，那么曼哈顿距离就指的是两点之间的实际距离（不一定是直线）。

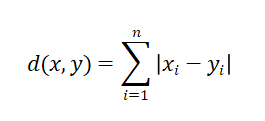
import numpy as np
from scipy.spatial.distance import pdist

x = np.array([1,2])
y = np.array([0,1])
dist = np.sum(np.abs(x-y))
print(dist)

dist2 = pdist(np.vstack([x,y]),'cityblock')
print(dist2)

③切比雪夫距离

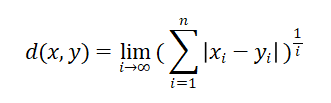
import numpy as np
from scipy.spatial.distance import pdist

x = np.array([1,2])
y = np.array([0,1])
dist = np.max(np.abs(x-y))
print(dist)

dist2 = pdist(np.vstack([x,y]),'chebyshev')
print(dist2)

④马氏距离

（Mahalanobis Distance）

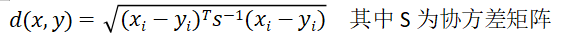
若协方差矩阵是单位矩阵，即各个样本向量之间独立同分布，则公式就变成了欧式距离：

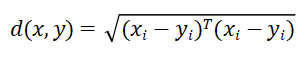
若协方差矩阵是对角矩阵，公式就变成了标准化欧式距离:

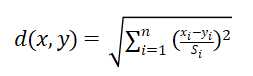
2.1.5 实例：判断电影的类型

import numpy as np
import operator
import matplotlib.pyplot as plt

def createDataSet():
    dataSet = np.array([[3,104],[2,100],[1,81],[101,10],[99,5],[98,2]])
    labels = ["爱情片","爱情片","爱情片","动作片","动作片","动作片"]
    return dataSet,labels

def classify0(inX,dataSet,labels,k):
    dataSetSize = dataSet.shape[0]
    diffMat = np.tile(inX,(dataSetSize,1))-dataSet
    sqDiffMat = diffMat**2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances**0.5
    sortedDistIndices = distances.argsort()
    classCount = {}
    for i in range(k):
        voteIlabel = labels[sortedDistIndices[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0)+1
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

if __name__=="__main__":
    dataSet,labels = createDataSet()
    result = classify0([23,111],dataSet,labels,5)
    print(result)

2.2 示例：使用k-近邻算法改进约会网站的配对效果

海伦将约会对象分为三类：①不喜欢的人②魅力一般的人③极具魅力的人。k-近邻算法步骤为：

1. 收集数据：提供文本文件
2. 准备数据：使用Python解析文本文件
3. 分析数据：使用Matplotlib画二维扩散图
4. 训练算法：此步骤不适用于k-近邻算法
5. 测试算法：使用海伦提供的部分数据作为测试样本。测试样本和非测试样本的区别在于：测试样本是已经完成分类的数据，如果预测分类与实际类别不同，则标记为一个错误。
6. 使用算法：产生简单的命令行程序，然后海伦可以输入一些特征数据以判断对方是否为自己喜欢的类型

2.2.1 准备数据：从文本文件中解析数据

约会数据存放在文件文件datingTestSet.txt中，每个样本数据占据一行，总共有1000行。海伦的样本主要包含以下3种特征：

• 每年获得的飞行常客里程数
• 玩视频游戏所耗时间百分比
• 每周消费的冰激淋公升数

在将上述特征数据输入到分类器之前，必须将待处理数据的格式改变为分类器可以接受的格式。在kNN.py中创建名为file2matrix的函数，以此来处理输入格式问题。该函数的输入为文件名字符串，输出为训练样本矩阵和类标签向量。

import numpy as np

"""
函数说明：打开并解析文件，对数据进行分类：1代表喜欢，2代表魅力一般，3代表极具魅力
Parameters：
    filename-文件名
Returns：
    returnMat-特征矩阵
    classLabelVector-分类Label向量
"""
def file2matrix(filename):
    #打开存储数据的文件
    fr = open(filename)
    #readlines() 方法用于读取所有行(直到结束符 EOF)并返回列表，
    #该列表可以由 Python 的 for... in ... 结构进行处理。
    #如果碰到结束符 EOF 则返回空字符串。
    arrayOLines = fr.readlines()
    #获取文件中有多少行数据
    numberOfLines = len(arrayOLines)
    #新建一个矩阵用来存放约会对象的三个特征
    returnMat = np.zeros([numberOfLines,3])
    #新建一个列表用来存放约会对象对应的喜欢程度
    classLabelVector = []
    #用来遍历returnMat
    index = 0
    #逐行获取样本数据
    for line in arrayOLines:
        #strip() 方法用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列。
        #注意：该方法只能删除开头或是结尾的字符，不能删除中间部分的字符。
        line = line.strip()
        #split()函数通常用于将字符串切片并转换为列表
        listFromLine = line.split('\t')
        #将约会对象的三个特征存储在returnMat中
        returnMat[index,:] = listFromLine[0:3]
        #根据喜欢程度存储相应的数字
        if listFromLine[-1]=="didntLike":
            classLabelVector.append(1)
        elif listFromLine[-1]=="smallDoses":
            classLabelVector.append(2)
        elif listFromLine[-1]=="largeDoses":
            classLabelVector.append(3)
        index+=1
    return returnMat,classLabelVector

if __name__=="__main__":
    returnMat,classLabelVector = file2matrix("datingTestSet.txt")
    print(returnMat)
    print(classLabelVector)

2.2.2 分析数据：使用Matplotlib创建散点图

import numpy as np
from matplotlib.font_manager import FontProperties
import matplotlib.lines as mlines
import matplotlib.pyplot as plt

"""
函数说明：打开并解析文件，对数据进行分类：1代表喜欢，2代表魅力一般，3代表极具魅力
Parameters：
    filename-文件名
Returns：
    returnMat-特征矩阵
    classLabelVector-分类Label向量
"""
def file2matrix(filename):
    #打开存储数据的文件
    fr = open(filename)
    #readlines() 方法用于读取所有行(直到结束符 EOF)并返回列表，
    #该列表可以由 Python 的 for... in ... 结构进行处理。
    #如果碰到结束符 EOF 则返回空字符串。
    arrayOLines = fr.readlines()
    #获取文件中有多少行数据
    numberOfLines = len(arrayOLines)
    #新建一个矩阵用来存放约会对象的三个特征
    returnMat = np.zeros([numberOfLines,3])
    #新建一个列表用来存放约会对象对应的喜欢程度
    classLabelVector = []
    #用来遍历returnMat
    index = 0
    #逐行获取样本数据
    for line in arrayOLines:
        #strip() 方法用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列。
        #注意：该方法只能删除开头或是结尾的字符，不能删除中间部分的字符。
        line = line.strip()
        #split()函数通常用于将字符串切片并转换为列表
        listFromLine = line.split('\t')
        #将约会对象的三个特征存储在returnMat中
        returnMat[index,:] = listFromLine[0:3]
        #根据喜欢程度存储相应的数字
        if listFromLine[-1]=="didntLike":
            classLabelVector.append(1)
        elif listFromLine[-1]=="smallDoses":
            classLabelVector.append(2)
        elif listFromLine[-1]=="largeDoses":
            classLabelVector.append(3)
        index+=1
    return returnMat,classLabelVector

"""
函数说明：可视化数据
Parameters：
    datingDataMat-特征矩阵
    datingLabels-分类label
Returns：
    无
"""
def showdatas(datingDataMat,datingLabels):
    #设置字体，不设置无法显示中文
    font = FontProperties(fname="siyuan.otf",size=14)
    """
    我们可以使用 pyplot 中的 **subplot()** 和 **subplots()** 方法来绘制多个子图。
    subplot() 方法在绘图时需要指定位置，**subplots()** 方法可以一次生成多个，在调用时只需要调用生成对象的 ax 即可。

    在matplotlib中，整个图像为一个Figure对象。在Figure对象中可以包含一个或者多个Axes对象。每个Axes(ax)对象都是一个拥有自己坐标系统的绘图区域。
    """
    fig,axs = plt.subplots(nrows=2,ncols=2,sharex=False,sharey=False,figsize=(13,8))
    #获得有多少个标签
    numberOfLabels = len(datingLabels)
    #设置画图时每行数据所对应点的颜色
    LabelsColors = []
    for i in datingLabels:
        if i==1:
            LabelsColors.append("black")
        if i==2:
            LabelsColors.append("orange")
        if i==3:
            LabelsColors.append("red")

    #画散点图
    axs[0][0].scatter(x=datingDataMat[:,0],y=datingDataMat[:,1],color=LabelsColors,s=15,alpha=.5)
    #返回值为代表标题的matplotlib文本实例
    axs0_title_text = axs[0][0].set_title("每年获得的飞行常客里程数与玩视频游戏所消耗时间占比",fontproperties=font)
    axs0_xlabel_text = axs[0][0].set_xlabel("每年获得的飞行常客里程数",fontproperties=font)
    axs0_ylabel_text = axs[0][0].set_ylabel("玩视频游戏所消耗时间占比",fontproperties=font)
    #setp()函数：设置对象属性或属性的取值要求
    plt.setp(axs0_title_text,size=9,weight="bold",color="red")
    plt.setp(axs0_xlabel_text,size=7,weight="bold",color="black")
    plt.setp(axs0_ylabel_text,size=7,weight="bold",color="black")

    axs[0][1].scatter(x=datingDataMat[:,0],y=datingDataMat[:,2],color=LabelsColors,s=15,alpha=.5)
    axs1_title_text = axs[0][1].set_title("每年获得的飞行常客里程数与每周消费的冰激淋公升数",fontproperties=font)
    axs1_xlabel_text = axs[0][1].set_xlabel("每年获得的飞行常客里程数",fontproperties=font)
    axs1_ylabel_text = axs[0][1].set_ylabel("每周消费的冰激淋公升数",fontproperties=font)
    plt.setp(axs1_title_text,size=9,weight="bold",color="red")
    plt.setp(axs1_xlabel_text,size=7,weight="bold",color="black")
    plt.setp(axs1_ylabel_text,size=7,weight="bold",color="black")

    axs[1][0].scatter(x=datingDataMat[:,1],y=datingDataMat[:,2],color=LabelsColors,s=15,alpha=.5)
    axs2_title_text = axs[1][0].set_title("玩视频游戏所消耗时间占比与每周消费的冰激淋公升数",fontproperties=font)
    axs2_xlabel_text = axs[1][0].set_xlabel("玩视频游戏所消耗时间占比",fontproperties=font)
    axs2_ylabel_text = axs[1][0].set_ylabel("每周消费的冰激淋公升数",fontproperties=font)
    plt.setp(axs2_title_text,size=9,weight="bold",color="red")
    plt.setp(axs2_xlabel_text,size=7,weight="bold",color="black")
    plt.setp(axs2_ylabel_text,size=7,weight="bold",color="black")

    #Line2D是matplotlib中专门负责线的类，也可以理解为专门用来画线的类
    didntLike = mlines.Line2D([],[],color="black",marker=".",markersize=6,label="didntLike")
    smallDoses = mlines.Line2D([],[],color="orange",marker=".",markersize=6,label="smallDoses")
    largeDoses = mlines.Line2D([],[],color="red",marker=".",markersize=6,label="largeDoses")

    #axes.legend()函数说明图例的位置等相关属性
    #legend handle：图例句柄， 用于在图例中生成合适的图例条目的原始对象
    axs[0][0].legend(handles=[didntLike,smallDoses,largeDoses])
    axs[0][1].legend(handles=[didntLike,smallDoses,largeDoses])
    axs[1][0].legend(handles=[didntLike,smallDoses,largeDoses])

    plt.show()

if __name__=="__main__":
    returnMat,classLabelVector = file2matrix("datingTestSet.txt")
    showdatas(returnMat,classLabelVector)

2.2.3 准备数据：归一化数值

在处理不同取值范围的特征值时，我们通常采用的方法是将数值归一化，如将取值范围处理为0到1或者-1到1之间。下面的公式可以将任意取值范围的特征值转化为0到1区间内的值。
$$newValue=(oldValue?min)/(max?min)$$
其中min和max分别是数据集中的最小特征值和最大特征值。

import numpy as np
from matplotlib.font_manager import FontProperties
import matplotlib.lines as mlines
import matplotlib.pyplot as plt

"""
函数说明：打开并解析文件，对数据进行分类：1代表喜欢，2代表魅力一般，3代表极具魅力
Parameters：
    filename-文件名
Returns：
    returnMat-特征矩阵
    classLabelVector-分类Label向量
"""
def file2matrix(filename):
    #打开存储数据的文件
    fr = open(filename)
    #readlines() 方法用于读取所有行(直到结束符 EOF)并返回列表，
    #该列表可以由 Python 的 for... in ... 结构进行处理。
    #如果碰到结束符 EOF 则返回空字符串。
    arrayOLines = fr.readlines()
    #获取文件中有多少行数据
    numberOfLines = len(arrayOLines)
    #新建一个矩阵用来存放约会对象的三个特征
    returnMat = np.zeros([numberOfLines,3])
    #新建一个列表用来存放约会对象对应的喜欢程度
    classLabelVector = []
    #用来遍历returnMat
    index = 0
    #逐行获取样本数据
    for line in arrayOLines:
        #strip() 方法用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列。
        #注意：该方法只能删除开头或是结尾的字符，不能删除中间部分的字符。
        line = line.strip()
        #split()函数通常用于将字符串切片并转换为列表
        listFromLine = line.split('\t')
        #将约会对象的三个特征存储在returnMat中
        returnMat[index,:] = listFromLine[0:3]
        #根据喜欢程度存储相应的数字
        if listFromLine[-1]=="didntLike":
            classLabelVector.append(1)
        elif listFromLine[-1]=="smallDoses":
            classLabelVector.append(2)
        elif listFromLine[-1]=="largeDoses":
            classLabelVector.append(3)
        index+=1
    return returnMat,classLabelVector

"""
函数说明：对数据进行归一化
Parameters:
    dataSet-特征矩阵
Returns:
    normDataSet-归一化后的特征矩阵
    ranges-数据范围
    minVals-数据最小值
"""
def autoNorm(dataSet):
    #获取数据的最小值
    #a.min()返回的就是a中所有元素的最小值
    #a.min(0)返回的就是a的每列最小值
    #a.min(1)返回的是a的每行最小值
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    #最大值和最小值的范围
    ranges = maxVals-minVals
    #创建一个与dataSet格式相同的矩阵用来存储归一化后的结果，用0初始化
    normDataSet = np.zeros(np.shape(dataSet))
    #返回dataSet的行数
    m = dataSet.shape[0]
    #原始值减去最小值
    normDataSet = dataSet-np.tile(minVals,(m,1))
    #除以取值范围，得到归一化结果
    normDataSet = normDataSet/np.tile(ranges,(m,1))
    #返回归一化数据结果，数据范围，最小值
    return normDataSet,ranges,minVals
    

if __name__=="__main__":
    returnMat,classLabelVector = file2matrix("datingTestSet.txt")
    normDataSet,ranges,minVals = autoNorm(returnMat)
    print(normDataSet)
    print(ranges)
    print(minVals)

2.2.4 测试算法：作为完整程序验证分类器

机器学习算法一个很重要的工作就是评估算法的正确率，通常我们只提供已有数据90%作为训练样本来训练分类器，而使用其余的10%数据去测试分类器，检测分类器的正确率。需要注意的是，10%的测试数据应该是随机选择的。

可以使用错误率来检测分类器的性能。对于分类器来说，错误率就是分类器给出错误结果的次数除以测试数据的总数，完美分类器的错误率为0，而错误率为1.0的分类器不会给出任何正确的分类结果。

我们可以定义一个计数器变量，每次分类器错误地分类数据，计数器就加1，程序执行完成之后计数器的结果除以数据点总数即是错误率。

import numpy as np
from matplotlib.font_manager import FontProperties
import matplotlib.lines as mlines
import matplotlib.pyplot as plt
import operator

"""
函数说明：打开并解析文件，对数据进行分类：1代表喜欢，2代表魅力一般，3代表极具魅力
Parameters：
    filename-文件名
Returns：
    returnMat-特征矩阵
    classLabelVector-分类Label向量
"""
def file2matrix(filename):
    #打开存储数据的文件
    fr = open(filename)
    #readlines() 方法用于读取所有行(直到结束符 EOF)并返回列表，
    #该列表可以由 Python 的 for... in ... 结构进行处理。
    #如果碰到结束符 EOF 则返回空字符串。
    arrayOLines = fr.readlines()
    #获取文件中有多少行数据
    numberOfLines = len(arrayOLines)
    #新建一个矩阵用来存放约会对象的三个特征
    returnMat = np.zeros([numberOfLines,3])
    #新建一个列表用来存放约会对象对应的喜欢程度
    classLabelVector = []
    #用来遍历returnMat
    index = 0
    #逐行获取样本数据
    for line in arrayOLines:
        #strip() 方法用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列。
        #注意：该方法只能删除开头或是结尾的字符，不能删除中间部分的字符。
        line = line.strip()
        #split()函数通常用于将字符串切片并转换为列表
        listFromLine = line.split('\t')
        #将约会对象的三个特征存储在returnMat中
        returnMat[index,:] = listFromLine[0:3]
        #根据喜欢程度存储相应的数字
        if listFromLine[-1]=="didntLike":
            classLabelVector.append(1)
        elif listFromLine[-1]=="smallDoses":
            classLabelVector.append(2)
        elif listFromLine[-1]=="largeDoses":
            classLabelVector.append(3)
        index+=1
    return returnMat,classLabelVector

"""
函数说明：对数据进行归一化
Parameters:
    dataSet-特征矩阵
Returns:
    normDataSet-归一化后的特征矩阵
    ranges-数据范围
    minVals-数据最小值
"""
def autoNorm(dataSet):
    #获取数据的最小值
    #a.min()返回的就是a中所有元素的最小值
    #a.min(0)返回的就是a的每列最小值
    #a.min(1)返回的是a的每行最小值
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    #最大值和最小值的范围
    ranges = maxVals-minVals
    #创建一个与dataSet格式相同的矩阵用来存储归一化后的结果，用0初始化
    normDataSet = np.zeros(np.shape(dataSet))
    #返回dataSet的行数
    m = dataSet.shape[0]
    #原始值减去最小值
    normDataSet = dataSet-np.tile(minVals,(m,1))
    #除以取值范围，得到归一化结果
    normDataSet = normDataSet/np.tile(ranges,(m,1))
    #返回归一化数据结果，数据范围，最小值
    return normDataSet,ranges,minVals
    
"""
函数说明：分类器

Parameters:
    inX-用于分类的输入向量（要对其进行分类的向量）
    dataSet-输入的训练样本集
    labels-标签向量，标签向量的元素数目和矩阵dataSet的行数相同
    k-用于选择最近邻居的数据
"""
def classify0(inX,dataSet,labels,k):
    #获取训练样本集的行数
    dataSetSize = dataSet.shape[0]
    #对输入向量进行复制，使其格式与dataSet相同，之后两个矩阵相减
    diffMat = np.tile(inX,(dataSetSize,1))-dataSet
    #对矩阵中的每个值进行乘方
    sqDiffMat = diffMat**2
    #sum就是求和，axis表示沿着axis方向求和
    #axis=1按行的方向相加，返回每行的值
    #axis=0按列的方向相加，返回每列的值
    sqDistances = sqDiffMat.sum(axis=1)
    #开根号后得到距离
    distances = sqDistances**0.5
    #numpy.argsort() 函数返回的是数组值从小到大的索引值。
    sortedDistIndicies = distances.argsort()
    #创建一个字典用于保存标签及其出现的次数
    classCount = {}
    for i in range(k):
        #将距离从小到大进行排序，并取得对应的标签
        voteIlabel = labels[sortedDistIndicies[i]]
        #统计对应标签出现的次数
        classCount[voteIlabel] = classCount.get(voteIlabel,0)+1
    #operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为一些序号。
    #参数为1表示对标签出现的次数进行排序，并且是从大到小排序
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    #获得对应的标签
    return sortedClassCount[0][0]


"""
函数说明：分类器测试函数
Parameters:
    无
Outputs:
    错误率
"""
def datingClassTest():
    #打开的文件
    filename = "datingTestSet.txt"
    #将返回的特征矩阵和分类向量分别存储到datingDataMat和datingLabels中
    datingDataMat,datingLabels = file2matrix(filename)
    #抽取所有数据的10%
    hoRatio = 0.10
    #数据归一化，返回归一化后的矩阵，数据范围，数据最小值
    normMat,ranges,minVals = autoNorm(datingDataMat)
    #获得normMat的行数
    m = normMat.shape[0]
    #10%的测试数据的个数
    numTestVecs = int(m*hoRatio)
    #分类错误计数
    errorCount = 0.0

    for i in range(numTestVecs):
        #前numTestVecs个数据作为测试集，后m-numTestVecs个数据作为训练集
        classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],4)
        print("分类结果：%d\t真实类别：%d" %(classifierResult,datingLabels[i]))
        if classifierResult!=datingLabels[i]:
            errorCount+=1.0
    print("错误率：%f%%" %(errorCount/float(numTestVecs)*100))


if __name__=="__main__":
    datingClassTest()

2.2.5 使用算法：构建完整可用系统

import numpy as np
from matplotlib.font_manager import FontProperties
import matplotlib.lines as mlines
import matplotlib.pyplot as plt
import operator

"""
函数说明：打开并解析文件，对数据进行分类：1代表喜欢，2代表魅力一般，3代表极具魅力
Parameters：
    filename-文件名
Returns：
    returnMat-特征矩阵
    classLabelVector-分类Label向量
"""
def file2matrix(filename):
    #打开存储数据的文件
    fr = open(filename)
    #readlines() 方法用于读取所有行(直到结束符 EOF)并返回列表，
    #该列表可以由 Python 的 for... in ... 结构进行处理。
    #如果碰到结束符 EOF 则返回空字符串。
    arrayOLines = fr.readlines()
    #获取文件中有多少行数据
    numberOfLines = len(arrayOLines)
    #新建一个矩阵用来存放约会对象的三个特征
    returnMat = np.zeros([numberOfLines,3])
    #新建一个列表用来存放约会对象对应的喜欢程度
    classLabelVector = []
    #用来遍历returnMat
    index = 0
    #逐行获取样本数据
    for line in arrayOLines:
        #strip() 方法用于移除字符串头尾指定的字符（默认为空格或换行符）或字符序列。
        #注意：该方法只能删除开头或是结尾的字符，不能删除中间部分的字符。
        line = line.strip()
        #split()函数通常用于将字符串切片并转换为列表
        listFromLine = line.split('\t')
        #将约会对象的三个特征存储在returnMat中
        returnMat[index,:] = listFromLine[0:3]
        #根据喜欢程度存储相应的数字
        if listFromLine[-1]=="didntLike":
            classLabelVector.append(1)
        elif listFromLine[-1]=="smallDoses":
            classLabelVector.append(2)
        elif listFromLine[-1]=="largeDoses":
            classLabelVector.append(3)
        index+=1
    return returnMat,classLabelVector

"""
函数说明：对数据进行归一化
Parameters:
    dataSet-特征矩阵
Returns:
    normDataSet-归一化后的特征矩阵
    ranges-数据范围
    minVals-数据最小值
"""
def autoNorm(dataSet):
    #获取数据的最小值
    #a.min()返回的就是a中所有元素的最小值
    #a.min(0)返回的就是a的每列最小值
    #a.min(1)返回的是a的每行最小值
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    #最大值和最小值的范围
    ranges = maxVals-minVals
    #创建一个与dataSet格式相同的矩阵用来存储归一化后的结果，用0初始化
    normDataSet = np.zeros(np.shape(dataSet))
    #返回dataSet的行数
    m = dataSet.shape[0]
    #原始值减去最小值
    normDataSet = dataSet-np.tile(minVals,(m,1))
    #除以取值范围，得到归一化结果
    normDataSet = normDataSet/np.tile(ranges,(m,1))
    #返回归一化数据结果，数据范围，最小值
    return normDataSet,ranges,minVals
    
"""
函数说明：分类器

Parameters:
    inX-用于分类的输入向量（要对其进行分类的向量）
    dataSet-输入的训练样本集
    labels-标签向量，标签向量的元素数目和矩阵dataSet的行数相同
    k-用于选择最近邻居的数据
"""
def classify0(inX,dataSet,labels,k):
    #获取训练样本集的行数
    dataSetSize = dataSet.shape[0]
    #对输入向量进行复制，使其格式与dataSet相同，之后两个矩阵相减
    diffMat = np.tile(inX,(dataSetSize,1))-dataSet
    #对矩阵中的每个值进行乘方
    sqDiffMat = diffMat**2
    #sum就是求和，axis表示沿着axis方向求和
    #axis=1按行的方向相加，返回每行的值
    #axis=0按列的方向相加，返回每列的值
    sqDistances = sqDiffMat.sum(axis=1)
    #开根号后得到距离
    distances = sqDistances**0.5
    #numpy.argsort() 函数返回的是数组值从小到大的索引值。
    sortedDistIndicies = distances.argsort()
    #创建一个字典用于保存标签及其出现的次数
    classCount = {}
    for i in range(k):
        #将距离从小到大进行排序，并取得对应的标签
        voteIlabel = labels[sortedDistIndicies[i]]
        #统计对应标签出现的次数
        classCount[voteIlabel] = classCount.get(voteIlabel,0)+1
    #operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为一些序号。
    #参数为1表示对标签出现的次数进行排序，并且是从大到小排序
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    #获得对应的标签
    return sortedClassCount[0][0]

"""
函数说明：通过输入一个人的三维特征，进行分类输出
Parameters:
    无
Returns:
    无
"""
def classifyPerson():
    #输出结果
    resultList = ["讨厌","有些喜欢","非常喜欢"]
    #三维特征用户输入
    percentTats = float(input("玩视频游戏所耗时间百分比："))
    ffMiles = float(input("每年获得的飞行常客里程数："))
    iceCream = float(input("每周消费的冰激凌公升数："))
    #打开的数据文件
    filename = "datingTestSet.txt"
    #打开并处理数据
    datingDataMat,datingLabels = file2matrix(filename)
    #训练集归一化
    normMat,ranges,minVals = autoNorm(datingDataMat)
    #生成numpy数组，测试集
    inArr = np.array([ffMiles,percentTats,iceCream])
    #测试集归一化
    norminArr = (inArr-minVals)/ranges
    #返回分类结果
    classifierResult = classify0(norminArr,normMat,datingLabels,3)
    #打印结果
    print("你可能%s这个人" %(resultList[classifierResult-1]))


if __name__=="__main__":
    classifyPerson()

2.3 示例：手写识别系统

构造系统识别数字0到9，其中数字采用文本格式进行存储。

使用k-近邻算法识别手写数字的步骤为：

1. 收集数据：提供文本文件
2. 准备数据：编写函数classify0()，将图像格式转换为分类器使用的list格式
3. 分析数据：在Python命令提示符中检查数据，确保它符合要求
4. 训练算法：此步骤不适用于k-近邻算法
5. 测试算法：编写函数使用提供的部分数据集作为测试样本，测试样本与非测试样本的区别在于测试样本是已经完成分类的数据，如果预测分类与实际类别不同，则标记为一个错误

2.3.1 准备数据：将图像转换为测试向量

为了使用前面的分类器，我们必须将图像格式化处理为一个向量。我们将把一个3232的二进制图像矩阵转换为11024的向量，这样就可以使用前面的分类器处理数字图像信息了。

首先编译一个函数img2vector，将图像转换为向量：该函数创建1*1024的Numpy数组，然后打开给定的文件，循环读出文件的前32行，并将每行的头32个字符值存储在Numpy数组中，最后返回数组。

import numpy as np
import os 

"""
函数说明:将32*32的二进制图像转换为1*1024向量
Parameters:
    filename-文件名
Returns:
    returnVect-返回的二进制图像的1*1024向量
"""
def img2vector(filename):
    returnVect = np.zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect
    
if __name__=="__main__":
    result = img2vector("./MachineLearning/KNN/0_0.txt")
    print(result[0,0:31])

2.3.2 测试算法：使用k-近邻算法识别手写数字

import numpy as np
import operator
from os import listdir

"""
函数说明：分类器

Parameters:
    inX-用于分类的输入向量（要对其进行分类的向量）
    dataSet-输入的训练样本集
    labels-标签向量，标签向量的元素数目和矩阵dataSet的行数相同
    k-用于选择最近邻居的数据
"""
def classify0(inX,dataSet,labels,k):
    #获取训练样本集的行数
    dataSetSize = dataSet.shape[0]
    #对输入向量进行复制，使其格式与dataSet相同，之后两个矩阵相减
    diffMat = np.tile(inX,(dataSetSize,1))-dataSet
    #对矩阵中的每个值进行乘方
    sqDiffMat = diffMat**2
    #sum就是求和，axis表示沿着axis方向求和
    #axis=1按行的方向相加，返回每行的值
    #axis=0按列的方向相加，返回每列的值
    sqDistances = sqDiffMat.sum(axis=1)
    #开根号后得到距离
    distances = sqDistances**0.5
    #numpy.argsort() 函数返回的是数组值从小到大的索引值。
    sortedDistIndicies = distances.argsort()
    #创建一个字典用于保存标签及其出现的次数
    classCount = {}
    for i in range(k):
        #将距离从小到大进行排序，并取得对应的标签
        voteIlabel = labels[sortedDistIndicies[i]]
        #统计对应标签出现的次数
        classCount[voteIlabel] = classCount.get(voteIlabel,0)+1
    #operator模块提供的itemgetter函数用于获取对象的哪些维的数据，参数为一些序号。
    #参数为1表示对标签出现的次数进行排序，并且是从大到小排序
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    #获得对应的标签
    return sortedClassCount[0][0]

"""
函数说明:将32*32的二进制图像转换为1*1024向量
Parameters:
    filename-文件名
Returns:
    returnVect-返回的二进制图像的1*1024向量
"""
def img2vector(filename):
    returnVect = np.zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

"""
函数说明:手写数字分类测试
Parameters:
    无
Returns:
    无
"""
def handwritingClassTest():
    #训练集的Labels
    hwLabels = []
    #os.listdir() 方法用于返回指定的文件夹包含的文件或文件夹的名字的列表。
    trainingFileList = listdir("./MachineLearning/KNN/trainingDigits")
    #获得文件夹中文件的数量
    m = len(trainingFileList)
    #初始化一个矩阵，用来存储训练集
    trainingMat = np.zeros([m,1024])
    for i in range(m):
        #获得各个文件的文件名
        fileNameStr = trainingFileList[i]
        #获得各个文件对应的数字，即对应的label
        classNumber = int(fileNameStr.split("_")[0])
        #将labels存储到hwLabels中
        hwLabels.append(classNumber)
        #将文件中的内容存储到矩阵trainingMat中
        trainingMat[i,:] = img2vector("./MachineLearning/KNN/trainingDigits/%s" %(fileNameStr))
    #获得测试集中的文件列表
    testFileList = listdir("./MachineLearning/KNN/testDigits")
    #记录错误的数量
    errorCount = 0.0
    #获得测试集文件的数量
    mTest = len(testFileList)
    for i in range(mTest):
        #获得每一个文件的文件名
        fileNameStr = testFileList[i]
        #获得对应的数字label
        classNumber = int(fileNameStr.split("_")[0])
        #获得对应测试文件的0*1024矩阵形式
        vectorUnderTest = img2vector("./MachineLearning/KNN/testDigits/%s" %(fileNameStr))
        #用分类器进行分类，本质就是判断距离，使得形状大致相似
        classifierResult = classify0(vectorUnderTest,trainingMat,hwLabels,3)
        print("分类返回结果为%d\t真实结果为%d" %(classifierResult,classNumber))
        if(classifierResult!=classNumber):
            errorCount+=1.0
    print("总共错了%d个数据\n错误率为%f%%" %(errorCount,errorCount/mTest*100))

"""
函数说明:main函数
Parameters:
    无
Returns:
    无
"""
if __name__=="__main__":
    handwritingClassTest()

2.4 示例：手写识别系统——sklearn实现

2.4.1 sklearn简介

Scikit learn也简称sklearn，是机器学习领域当中最知名的python模块之一。sklearn包含了很多机器学习的方式：

• Classification分类
• Regression回归
• Clustering非监督分类
• Dimensionality reduction数据降维
• Model Selection模型选择
• Preprocessing数据与处理

使用sklearn可以很方便地让我们实现一个机器学习算法。一个复杂的算法的实现，使用sklearn可能只需要调用几行API即可。

2.4.2 sklearn实现k-近邻算法简介

sklearn.neighbors模块实现了k-近邻算法。我们使用sklearn.neighbors.KNeighborsClassifier可以实现我们之前实现的k-近邻算法。KNeighborsClassifier函数一共有八个参数：

• n_neightbors：默认为5，就是k-NN的k的值，选取最近的k个点
• weights：默认是uniform，参数可以是uniform、distance，也可以是用户自己定义的函数。uniform是均等的权重，就说所有的邻近点的权重都是相等的。distance是不均等的权重，距离近的点比距离远的点的影响大。用户自定义的函数，接收距离的数组，返回一组维数相同的权重。
• algorithm：快速k近邻搜索算法，默认参数为auto，可以理解为算法自己决定合适的搜索算法。
• leaf_size：默认是30，这个是构造的kd树和ball树的大小。这个值的设置会影响树构建的速度和搜索速度，同样也影响着存储树所需的内存大小。需要根据问题的性质选择最优的大小。
• metric：用于距离度量，默认度量是minkowski，也就是p=2的欧氏距离(欧几里德度量)。
• p：距离度量公式。在上小结，我们使用欧氏距离公式进行距离度量。除此之外，还有其他的度量方法，例如曼哈顿距离。这个参数默认为2，也就是默认使用欧式距离公式进行距离度量。也可以设置为1，使用曼哈顿距离公式进行距离度量。
• metric_params：距离公式的其他关键参数，这个可以不管，使用默认的None即可。
• n_jobs：并行处理设置。默认为1，临近点搜索并行工作数。如果为-1，那么CPU的所有cores都用于并行工作。

KNeighborsClassifier可以调用的方法有：

• fit(X,y)：从训练数据集拟合k近邻分类器。
• get_params([deep])：为这个估计器获取参数。
• kneighbors([X,n_neighbors,return_distance])：找出一个点的k邻居。
• predict(x)：预测所提供数据的类标签。
• predict_proba(x)：返回测试数据X的概率估计。
• score(x,y[,sample_weight])：返回给定测试数据和标签的平均精度。
• set_params：设置这个估计器的参数。

2.4.3 系统实现

import numpy as np
import operator
from os import listdir
from sklearn.neighbors import KNeighborsClassifier as kNN

"""
函数说明:将32*32的二进制图像转换为1*1024向量
Parameters:
    filename-文件名
Returns:
    returnVect-返回的二进制图像的1*1024向量
"""
def img2vector(filename):
    returnVect = np.zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

"""
函数说明:手写数字分类测试
Parameters:
    无
Returns:
    无
"""
def handwritingClassTest():
    #训练集的labels
    hwLabels = []
    #os.listdir() 方法用于返回指定的文件夹包含的文件或文件夹的名字的列表。
    trainingFileList = listdir("./MachineLearning/KNN/trainingDigits")
    #获得文件夹中文件的数量
    m = len(trainingFileList)
    #初始化一个矩阵，用来存储训练集
    trainingMat = np.zeros([m,1024])
    for i in range(m):
        #获得各个文件的文件名
        fileNameStr = trainingFileList[i]
        #获得各个文件对应的数字，即对应的label
        classNumber = int(fileNameStr.split("_")[0])
        #将label存储到hwLabels中
        hwLabels.append(classNumber)
        #将文件中的内容存储到矩阵trainingMat中
        trainingMat[i,:] = img2vector("./MachineLearning/KNN/trainingDigits/%s" %(fileNameStr))
    #创建一个kNN分类器
    neigh = kNN(n_neighbors=3,algorithm="auto")
    #用训练集矩阵和训练集labels对kNN分类器进行拟合
    neigh.fit(trainingMat,hwLabels)
    #获得测试集中的文件列表
    testFileList = listdir("./MachineLearning/KNN/testDigits")
    #记录错误的数量
    errorCount = 0.0
    #获得测试集文件的数量
    mTest = len(testFileList)
    for i in range(mTest):
        #获得每一个文件的文件名
        fileNameStr = testFileList[i]
        #获得对应的数字label
        classNumber = int(fileNameStr.split("_")[0])
        #获得对应测试文件的0*1024矩阵形式
        vectorUnderTest = img2vector("./MachineLearning/KNN/testDigits/%s" % (fileNameStr))
        #用kNN分类器对测试数据进行预测
        classifierResult = neigh.predict(vectorUnderTest)
        print("分类返回结果为%d\t真实结果为%d" %(classifierResult,classNumber))
        if(classifierResult!=classNumber):
            errorCount+=1.0
    print("总共错了%d个\n错误率为%f%%" %(errorCount,errorCount/mTest*100))

"""
函数说明:main函数
Parameters:
    无
Returns:
    无
"""
if __name__=="__main__":
    handwritingClassTest()

2.5 本章小结

• k-近邻算法是基于实例的学习，使用算法时我们必须有接近实际数据的训练样本数据。k-近邻算法必须保存全部数据集，如果训练数据集很大，必须使用大量的存储空间。此外，由于必须对数据集中的每个数据计算距离值，实际使用时可能非常耗时。
• k-近邻算法的另一个缺陷是它无法给出任何数据的基础结构信息，因此我们也无法知晓平均实例样本和典型实例样本具有什么特征。

参考

1. 常用的向量距离公式_Begining-CSDN博客_向量距离公式
2. https://cuijiahua.com/blog/2017/11/ml_1_knn.html