[数据结构与算法]球面双站交叉定位计算方法

写在前面

之前自己写的word丢了，为避免丢失，在网上发一下，主要是备忘，有些表达不严谨请，见谅。

方法和模型图片来自引文:张静.杜剑平.蒋俊,基于球体模型的短波固定多站交叉定位选站方法[j].信息工程大学学报,2020,(1),9-14 26

再吐槽知网:下个论文收费3.5，表示理解；充值最小30，每次下载都要收一遍，手机app上藏得老深了，我就想要张图，有这功夫自己都画出来了。

另外，电脑没在身边，手机码字，写公式不易，转发引用请注明出处。

计算模型

当目标与侧向站不在同一平面时，侧向交叉定位必须考虑地球曲率的影响，将地球看成球体，半径$R=6731km$,考虑到侧向误差远大于地球椭球偏心率影响，简化计算把地球看成正球。此时，侧向交叉定位如图1所示。

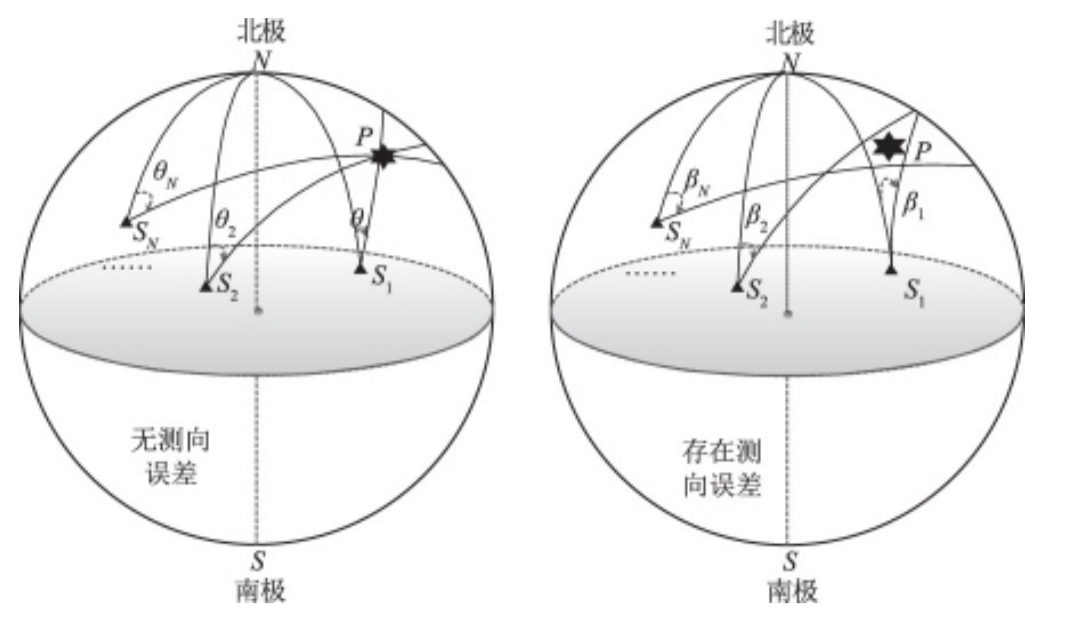
图中$P({?}_s,{\lambda }_s)$为辐射源;$S_n({?}_n,{\lambda }_n),n=1,2,3...$,为侧向站，${\theta }_n$为$S_n$对$P$的侧向角真实值，${\beta }_n$为测量值。
为便于描述观察模型，建立以球形为原点的空间大地坐标系，用纬度$?$，经度$\lambda$和大地高$H$来表示空间位置，如图2所示。

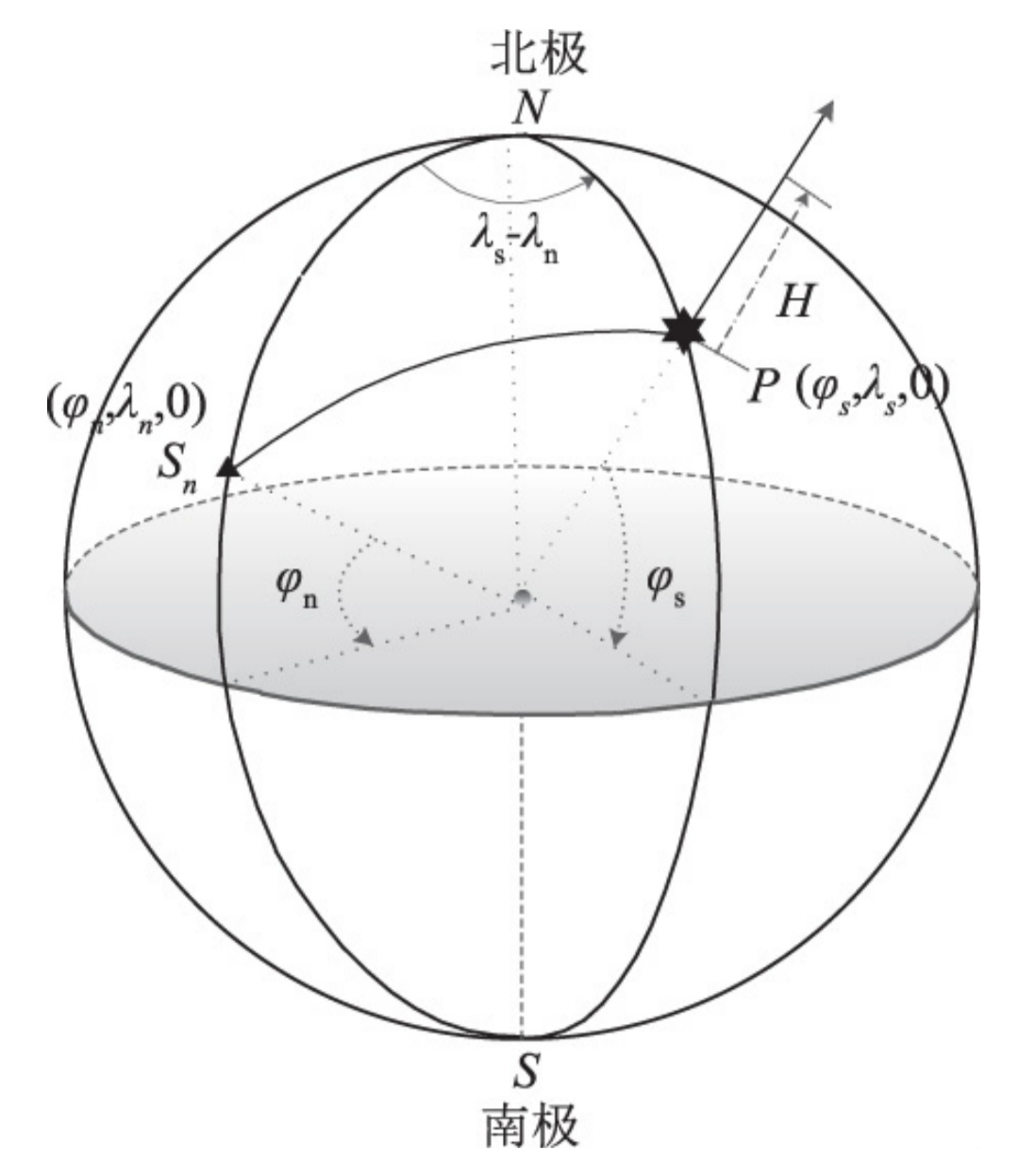
在空间大地坐标系中，$S_n$的坐标为$S_n({?}_n,{\lambda }_n,0),P({?}_s,{\lambda }_s,0)$,两点与北极点形成球面三角形$S_{n}NP$，以$\stackrel{?}{S_{n}N},\stackrel{?}{S_{n}P},\stackrel{?}{\mathrm{NP}}$表示球面三角形大圆弧，以球面角$\angle N{S}_{n}P,\angle PN{S}_n,\angle NP{S}_n$表示球面三角形中的三个角,则由球面三角形的余切定理可得:$\cot (\angle N{S}_{n}P)\sin (\angle PN{S}_n)=\cot (\stackrel{?}{\mathrm{NP}})\sin (\stackrel{?}{S_{n}N})?\cos (\stackrel{?}{S_{n}N})\cos (\angle PN{S}_n)$ (1)
由经纬度的定义可知:
$?\begin{array}{rl}\angle PN{S}_n& ={\lambda }_s?{\lambda }_n\\ \stackrel{?}{S_{n}N}& =\frac{\pi }{2}?{?}_n\\ \stackrel{?}{\mathrm{NP}}& =\frac{\pi }{2}?{?}_s\end{array}$ (2)
由侧向角的定义可知:
$\angle N{S}_{n}P={\theta }_n$ (3)

求解过程

将式(2)(3)代入(1)得:
$\cot (\theta )\sin ({\lambda }_s?{\lambda }_n)=\cot (\frac{\pi }{2}?{?}_s)\sin (\frac{\pi }{2}?{?}_n)?\cos (\frac{\pi }{2}?{?}_n)\cos ({\lambda }_s?{\lambda }_n)$ (4)
即:
$\frac{\sin {\theta }_n}{\cos {\theta }_n}=\frac{\cos {?}_s\sin ({\lambda }_s?{\lambda }_n)}{\cos {?}_n\sin {?}_s?\sin {?}_n\cos {?}_s\cos ({\lambda }_s?{\lambda }_n)}$ (5)
和差化积:
$\frac{\sin {\theta }_n}{\cos {\theta }_n}=\frac{\cos {?}_s(\sin {\lambda }_s\cos {\lambda }_n?\cos {\lambda }_s\sin {\lambda }_n)}{\cos {?}_n\sin {?}_s?\sin {?}_n\cos {?}_s(\cos {\lambda }_s\cos {\lambda }_n+\sin {\lambda }_s\sin {\lambda }_n)}$ (6)
令已知数:$a,b,c,d,e,f=\sin {\lambda }_n,\cos {\lambda }_n,\sin {?}_n,\cos {?}_n,\sin {\theta }_n,\cos {\theta }_n$ (7)
令未知数:$x,y,u,v=\sin {\lambda }_s,\cos {\lambda }_s,\sin {?}_s,\cos {?}_s$ (8)
将(7)(8)代入(6)简化后得:
$edu=(ecf?fa)vy+(eca+fb)vx$ (9)
令已知数:
$l_i=ed,m_i=ecb?fa,n_i=ca?fb,i=1or2$(10)
将(10)代入(9)简化后:
$l_{i}u=m_{i}vy+n_{i}x$ (11)
已知两个侧向站的坐标和基本三角公式可联立方程组:
$?\begin{array}{rl}{l}_{1}u& =m_{1}vy+n_{1}x\\ l_{2}u& =m_{2}vy+n_{2}x\\ 1& =x^2+y^2\\ 1& =u^2+v^2\end{array}$ (12)
令已知数:
$A=\frac{l_1{n}_2?l_2{n}_1}{l_2{m}_1?l_1{m}_2}$ (13)
如果$l_2{m}_1?l_1{m}_2=0$,辐射源经度为0或180度，或者3点在同一经线圆上。
得到2组经度解:
$x=\pm \sqrt{\frac{1}{A^2+1}},y=Ax$ (14)
令已知数:
$B=\frac{m_{i}y+n_{i}x}{l_i}$ (15)
由(14)代入可知B有2个值，已知数，也可以使用1号或者2号侧向站代入计算，避免$l_i=0$,如果$l_1=l_2=0$,代表$P$在两极。
得到2组纬度解:
$v=\pm \sqrt{\frac{1}{B^2+1}},u=Bv$ (16)
对应每个$A$有2个解，共4组解。
分别对$(x,y),(u,v)$使用atan2函数计算经纬度得到4组经纬度坐标，其中两组纬度坐标不在$[?\frac{\pi }{2},\frac{\pi }{2}]$范围内，剔除后得到两组坐标，是球面上的过心对称点。
是用Haversin函数，分别求两个侧向站到两组坐标的距离，得到4个值，其中最小值就是目标点到其中一个站的最小距离，对应的坐标就是最终目标点$P({?}_s,{\lambda }_s)$的坐标。

Python 测试代码

import numpy as np
import math

def get_lmn(s):
    lon,lat,az = s
    a,b,c,d,e,f = np.sin(lon),np.cos(lon),np.sin(lat),np.cos(lat),np.sin(az),np.cos(az)
    return (e*d,e*c*b-f*a,e*c*a+f*b)

def cov2cood(sincos):
    claCoord = lambda scsc:(math.atan2(scsc[2],scsc[3]),math.atan2(scsc[0],scsc[1]))
    result = [claCoord(sincos[0]),claCoord(sincos[1]),claCoord(sincos[2]),claCoord(sincos[3])]
    return np.rad2deg(result)


#在s点在p1,p2 的连线上，没有处理
def cross_location(s1,s2):
    '''
    目标点为S(xlon,xlat)
    点P(lon,lat,az)与S的关系(1)
    (1):sin(az)/cos(az) = cos(xlat)sin(xlon-lon)/[cos(lat)sin(xlat)-sin(lat)cos(xlat)cos(xlon-lon)]
    令x,y,u,v = sin(xlon),cos(xlon),sin(xlat),cos(xlat)
    (1)可将简化为(2):l*u=m*vy+n*vx
    两点分别带入(2),得到2个方程
    加上(3):u^2+v^2=1，(4):x^2+y^2=1,共4个方程形成的4元2次方程组
    令 a = (l1*n2-l2*n1)/(l2*m1-l1*m2)
    x=±√(1/(a^2+1)),y=ax
    令 b = (m1*y+n1*x)/l2,换成m2,n2,l2也可以
    v=±√(1/(b^2+1)),u=bv
    得到4组(x,y,u,v)
    换算成经纬角(arctan2(x,y),arctan2(u,v)) =>(xlon,xlat) 
    排除xlat < -pi/2 ,或 xlat > pi/2 ,只剩两组坐标
    这两个点是过心对称点
    '''
    s1 = np.deg2rad(s1)
    s2 = np.deg2rad(s2)
    l1,m1,n1 = get_lmn(s1)
    l2,m2,n2= get_lmn(s2)
    if (l2*m1-l1*m2) != 0:
        A = (l1*n2-l2*n1)/(l2*m1-l1*m2) 
        X = np.array([np.sqrt(1/(A**2+1)),-np.sqrt(1/(A**2+1))])
        Y = A * X
    else:
        X = np.array([0,0])
        Y = np.array([1,-1])
    #防止除0错误
    if l1!=0 or l2!=0:
        L,M,N = l1,m1,n1
        if l1 == 0:
            L,M,N = l2,m2,n2
        calb = lambda x,y:(M*y+N*x)/L
        b0 = calb(X[0],Y[0])
        b1 = calb(X[1],Y[1])
        V0 = np.array([np.sqrt(1/(b0**2+1)),-np.sqrt(1/(b0**2+1))])
        U0 = V0*b0
        V1 = np.array([np.sqrt(1/(b1**2+1)),-np.sqrt(1/(b1**2+1))])
        U1 = V1*b1
    else:
        # cos(lat)不会为0 ，不然就az就没有意义只有 sin(az)==0 即az均为 =0 或 180，指向极点 
        U0=[1,1]
        U1=[-1,1]
        V0=[0,-0.1]
        V1=[0,-0.1] 
    result = [(U0[0],V0[0],X[0],Y[0]),(U0[1],V0[1],X[0],Y[0]),(U1[0],V1[0],X[1],Y[1]),(U1[1],V1[1],X[1],Y[1])]
    result = cov2cood(result)
    frsl = []

    for i in range(4):
        lat = result[i][1] 
        if lat>= -90 and lat <=90:
            frsl.append(result[i])
    return np.array(frsl)

def distance_haversine(p1,p2,r=1):
    '''
    hav(x) = sin(x/2)^2 = (1-cos(x))/2
    a(alpha) 两点过心角
    hav(a) = hav(lat1-lat2)+cos(lat1)*cos(lat2)*hav(lon1-lon2)
    input:
    p1:[lon,lat] in degree
    p2:[lon,lat] in degree
    r:球半径
    return:球面距离
    '''
    p1=np.deg2rad(p1)
    p2=np.deg2rad(p2)
    hav_lon = math.sin((p1[0]-p2[0])/2)**2
    hav_lat = math.sin((p1[1]-p2[1])/2)**2
    hav_a = hav_lat + math.cos(p1[1])*math.cos(p2[1])*hav_lon
    a = 2*math.atan2(math.sqrt(hav_a),math.sqrt(1-hav_a))
    return a*r

def distance_greate_circle(p1,p2,r=1):
    '''
    使用弦长计算角,求弧长
    '''
    dpp = distance_chord_line(p1,p2)
    #余弦定理求角
    a = math.acos((2-dpp**2)/2)
    return r*a
    

def distance_chord_line(p1,p2,r=1):
    '''
    计算弦长
    x= cos(lat)sin(lon)
    y= cos(lat)cos(lon)
    z= sin(lat)
    '''
    to_xyz = lambda lon,lat:(math.cos(lat)*math.sin(lon),math.cos(lat)*math.cos(lon),math.sin(lat))
    p1=np.deg2rad(p1)
    p2=np.deg2rad(p2)
    p1 = to_xyz(p1[0],p1[1])
    p2 = to_xyz(p2[0],p2[1])
    d = (p1[0]-p2[0])**2+(p1[1]-p2[1])**2+(p1[2]-p2[2])**2
    d = math.sqrt(d)
    return r*d

def pick_nearest_root(s1,s2,roots):
    '''
    选出离侧向站最近的点
    '''
    nroot = len(roots)
    adist = []
    for i in range(nroot):
        adist.append(distance_chord_line(s1,roots[i]))
        adist.append(distance_chord_line(s2,roots[i]))
    minv = math.pi*2
    min_i = 0
    for i in range(len(adist))  :
        if minv > adist[i] :
            minv = adist[i]
            min_i = i
    return roots[min_i//2]

def cross_location_nearest(s1,s2):
    roots = cross_location(s1,s2)
    return pick_nearest_root(s1[:2],s2[:2],roots)

if __name__ == "__main__":
    s1,s2 = [61.1,32.2,120],[52,28.1,33]
    print("s1[lon,lat,az]  ---------------------------\n",s1)
    print("s2[lon,lat,az]  ---------------------------\n",s2)
    locs = cross_location(s1,s2)
    print("roots of equation set[lon,lat]  -----------\n",locs)
    loc=cross_location_nearest(s1,s2)
    print("nearest loaction[lon,lat]  ----------------\n",loc)
    print("dist to s1  ---------------------------\n",distance_haversine(s1[:2],loc))
    print("dist to s2  ---------------------------\n",distance_haversine(s2[:2],loc))