须知
通常情况下，竞赛环境中要求运行时间为1秒。计算机1秒可以执行的次数为10亿次。但是我们做题时要把次数限定在1亿次，也就是10^8。
一维前缀和
显然，对于这道题如果用比较暴力的思想，遍历加的话，时间复杂度是O(10^5 * 10^5)会超时，所以要用前缀和算法求解。
我们可以定义一个数组s，s[i]它表示前i个数字的和.
比如我们要求a[2] + a[3] + a[4]，其实就等于s[4] - s[1]。那么我们的复杂度就落在了求s数组上，其是一个线性复杂度即O(n)，所以肯定不会超时。
一维前缀和求法：s[i] = s[i - 1] + a[i]
子区域求法：s[r] - s[l - 1]
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, m;
int l, r;
int a[N];
int s[N]; //s为前缀和
int main()
{
cin >> n >> m;
//输入a数组
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
//计算前缀和数组
for (int i = 1; i <= n; i++)
{
s[i] = s[i - 1] + a[i];
}
for (int i = 0; i < m; i++)
{
cin >> l >> r;
cout << s[r] - s[l -1] <<endl;
}
return 0;
}
二维前缀和
二维前缀和记录的是在一个二维矩阵中，从左上角开始到矩阵的某个点构成的子矩阵中所有元素的和。
同理，这个问题也不能用暴力方法解决，要用前缀和思想解决。
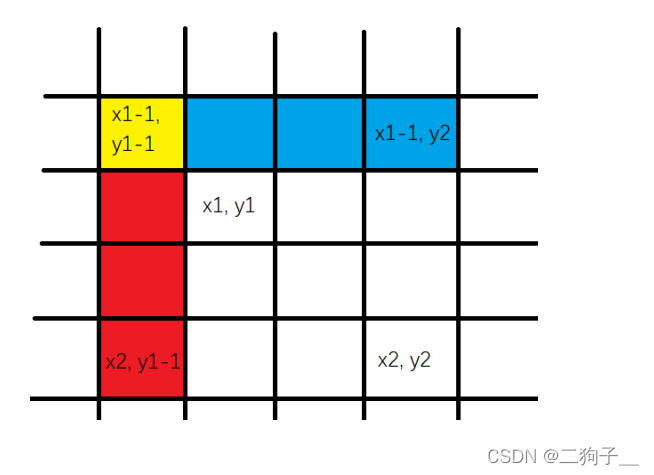
二维前缀和求法：s[x][y] = s[x - 1][y] + s[x][y -1] - s[x -1][y-1] + a[x][y]
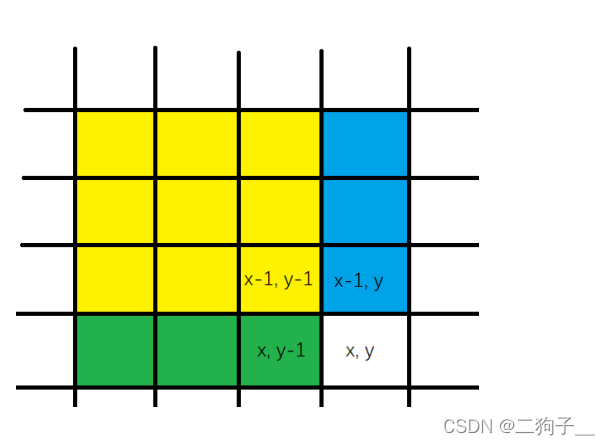
子区域求法：s = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 -1]
代码
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int a[N][N];
int s[N][N]; //二维前缀和
int n, m, q;
int main()
{
cin >> n >> m >> q;
//输入a数组
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> a[i][j];
}
}
//构造二维前缀和数组
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + a[i][j];
}
}
//输出
int x1, y1, x2, y2;
for (int i = 0; i < q; i++)
{
cin >> x1 >> y1 >> x2 >> y2;
cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;
}
return 0;
}
一维差分
题目传送门
我们可以通过对差分数组b的操作，来达到使a数组发生相应变化。
代码
#include<bits/stdc++.h>
using namespace std;
int n, m;
int l ,r, c;
int a[100010], b[100010];
int main()
{
//输入
cin >> n >> m;
for (int i = 1; i <= n; i++) {
cin >> a[i];
b[i] = a[i] - a[i - 1];
}
//变换b数组
for (int i = 0; i < m; i++) {
cin >> l >> r >> c;
b[l] += c;
b[r + 1] -= c;
}
//还原a数组（一维前缀和）（这里直接用b数组算也行，不一定非得算出a数组）
for (int i = 1; i <= n; i++) {
b[i] += b[i - 1];
cout << b[i] << " ";
}
return 0;
}
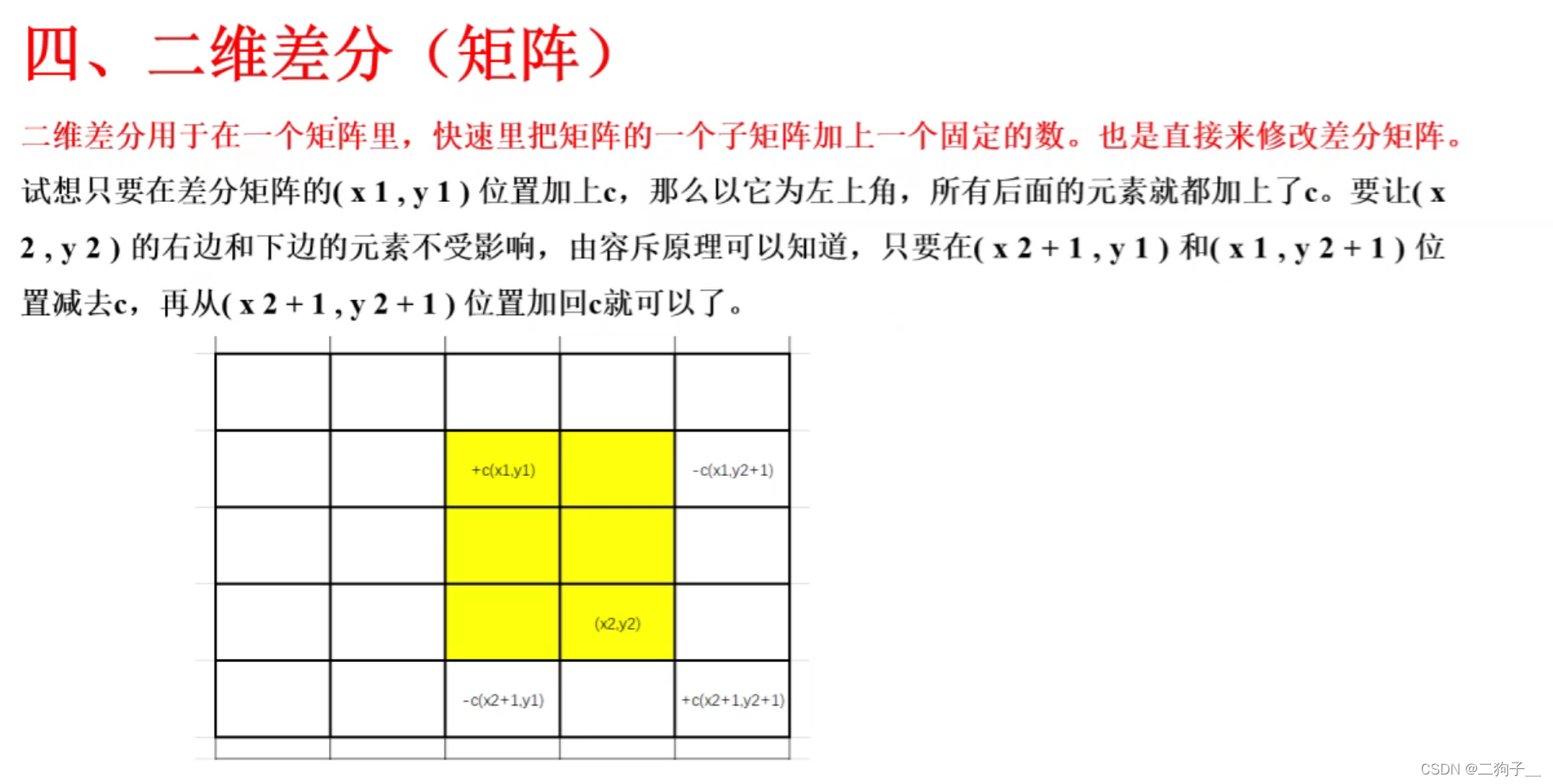
二维差分
代码
#include<bits/stdc++.h>
using namespace std;
int n, m, q;
int a[1010][1010], b[1010][1010];
void insert(int x1, int y1, int x2, int y2, int c) {
b[x1][y1] += c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
int x1, y1, x2, y2, c;
//输入并构造b数组
cin >> n >> m >> q;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
insert(i, j, i, j, a[i][j]);
}
}
//变换b数组
for (int i = 0; i < q; i++) {
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
}
//还原a数组（二维前缀和）（这里用b数组算也行，不一定非得算出a数组）
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
b[i][j] = b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1] + b[i][j];
cout << b[i][j] << " ";
}
cout << endl;
}
return 0;
}
作业
这道题本质就是一维差分。
代码
#include<bits/stdc++.h>
using namespace std;
int n, x, y;
int b[100010];
int main()
{
while (1) {
//输入
cin >> n;
if (n == 0) break;
//变换b数组
for (int i = 0; i < n; i++) {
cin >> x >> y;
b[x]++;
b[y + 1]--;
}
//还原a数组（一维前缀和）(这里用b数组算也行，不一定非得算出a数组)
for (int i = 1; i <= n; i++) {
b[i] += b[i - 1];
cout << b[i] <<" ";
}
cout << endl;
//b数组清空
memset(b, 0, sizeof(b));
}
return 0;
}