[数据结构与算法]蓝桥杯 floyd算法练习 最短路

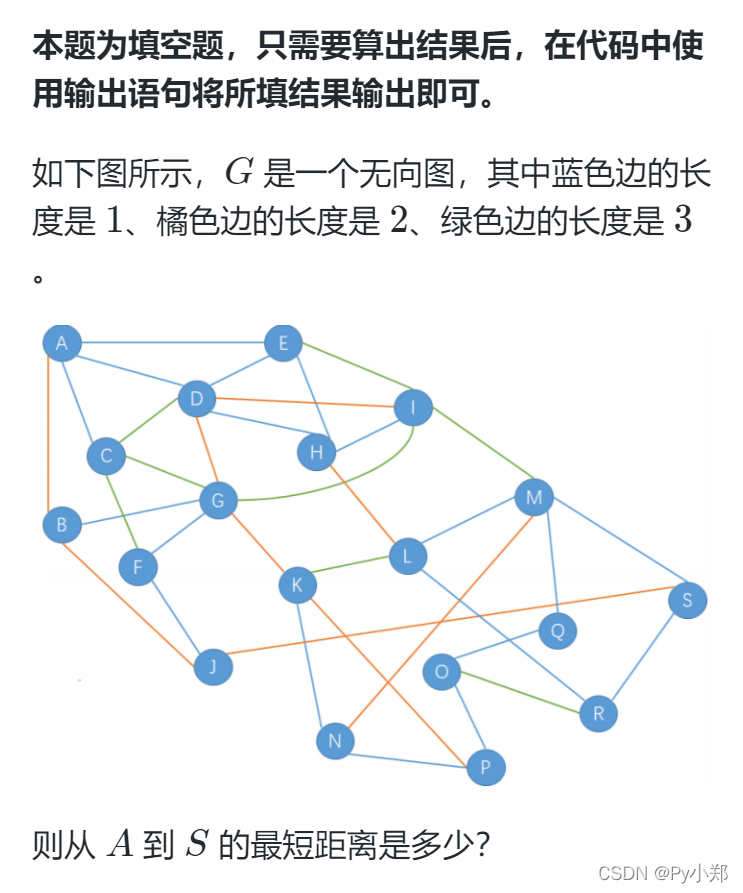
问题描述：

?看这个问题之前可以先看看这个这个up主讲的 很详细😀（有助于对下面核心代码的理解）

求最短路径Floyd算法！_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV14R4y1x7GB

?问题分析：我的难点就在于数据初始化 由于这是个无向图

那么必有graph[i][j]=graph[j][i]

即临接矩阵对称

然后我是手动输入的= =输了大概快7—8分钟

然后总结了下面几点规律：

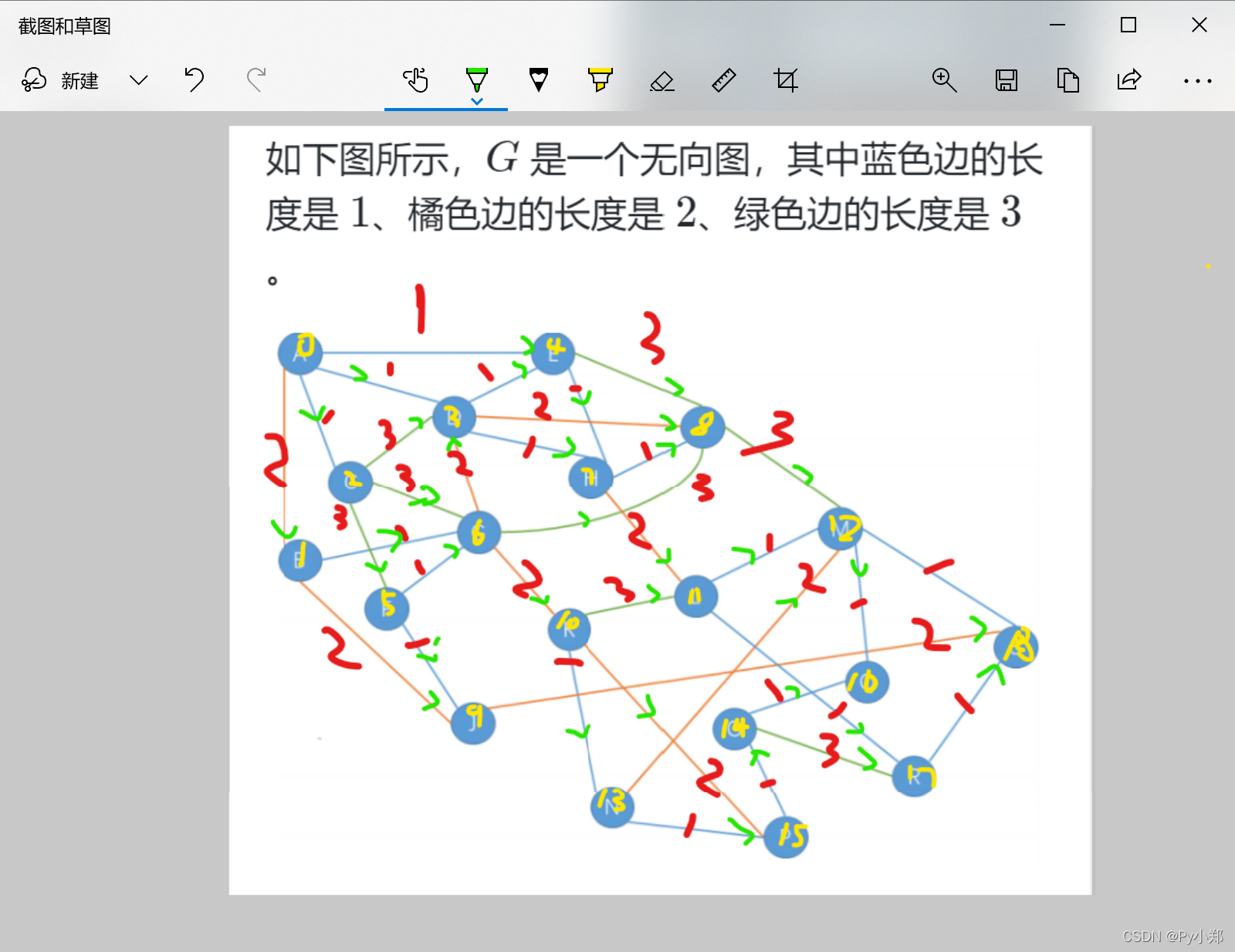
对于无向图求最短路径 先把图标上箭头转化为有向图

权值用数字标出

每个地点用数字标出

最后利用对称的性质 大概可以把输入数据的时间缩小到5分钟左右

再其次就是floyd的算法 三行经典代码 今天算是体会到了

datas=[
    [0,0,0],
    [0,1,2],
    [0,2,1],
    [0,3,1],
    [0,4,1],
    [1,1,0],
    [1,0,2],
    [1,6,1],
    [1,9,2],
    [2,2,0],
    [2,0,1],
    [2,3,3],
    [2,5,3],
    [2,6,3],
    [3,3,0],
    [3,0,1],
    [3,4,1],
    [3,8,2],
    [3,6,2],
    [4,4,0],
    [4,0,1],
    [4,3,1],
    [4,7,1],
    [4,8,3],
    [5,5,0],
    [5,2,3],
    [5,6,1],
    [5,9,1],
    [6,6,0],
    [6,1,1],
    [6,2,3],
    [6,3,2],
    [6,10,2],
    [6,8,2],
    [6,5,1],
    [7,7,0],
    [7,3,1],
    [7,4,1],
    [7,8,1],
    [7,11,2],
    [8,8,0],
    [8,3,2],
    [8,4,3],
    [8,12,3],
    [8,7,1],
    [9,9,0],
    [9,1,2],
    [9,5,1],
    [9,18,2],
    [10,10,0],
    [10,6,2],
    [10,11,3],
    [10,13,1],
    [10,15,2],
    [11,11,0],
    [11,10,3],
    [11,7,2],
    [11,12,1],
    [11,17,1],
    [12,12,0],
    [12,8,3],
    [12,11,1],
    [12,13,2],
    [12,10,1],
    [12,18,1],
    [13,13,0],
    [13,10,1],
    [13,12,2],
    [13,15,1],
    [14,14,0],
    [14,16,1],
    [14,15,1],
    [14,17,3],
    [15,15,0],
    [15,14,1],
    [15,10,2],
    [15,13,1],
    [16,16,0],
    [16,12,1],
    [16,14,1],
    [17,17,0],
    [17,11,1],
    [17,14,3],
    [17,18,1],
    [18,18,0],
    [18,17,1],
    [18,9,2],
    [18,12,1]
]
graph=[[float('inf')]*19 for i in range(19)]
for u,v,c in datas:
    graph[u][v]=c
for k in range(19):#以k为中转站
    for i in range(19):
        for j in range(19):
            graph[i][j]=min(graph[i][j],graph[i][k]+graph[k][j])
print(graph[0][18])

这是我一开始的做法，比较笨 比如输入了[11,12,1]，实际上[12,11,1]就不用在输入了

我们只需要在最外层循环补上graph[v][u]=c即可 答案是6

????????????????题目链接最短路传送门

特别感谢以下这位博主的讲解 强推！?很适合和小郑一样刚入门的去看 真的很OK！
floyd算法(多源最短路径) python实现_Aiven-CSDN博客_floyd算法python代码https://blog.csdn.net/AivenZhong/article/details/93770197?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164387396216780261917064%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=164387396216780261917064&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-2-93770197.first_rank_v2_pc_rank_v29&utm_term=floyd%E7%AE%97%E6%B3%95+python&spm=1018.2226.3001.4187