概念
在理解概念之前,我们首先需要知道何谓大数字?
大数字:大数字就是如15156156156151151这样庞大的数字,大数字都有一个共同特征:普通的存储类型无法存储,由此我们引进了高精度算法。
高精度算法:高精度算法是一种通过数组进行存储数字的算法。
如:6515158912823478952在数组中的存储如下:
高精度加法
主要思想:用字符数组进行接收数字,将数字逐一逆序存储到数组中,对应位置依次相加。
在此之前,我们回忆一下小学加法的做法:
1.对应位置相加
2.逢十进一
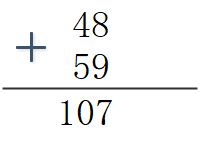
(1)8+9=17,逢十进一,17%10得到个位存储的数字为7。
(2)4+5+1=10,逢十进一,10%10得到个位存储的数字为0。
(3)两个数字百位都没有数字了,所以百位存储的数字就为1。
(4)得到答案107。
高精度加法步骤:
(1):字符数组存储大数字
(2):逆序插入整形数组
(3):对应位置数字相加,并进行%10运算存储到数组中,逢十进一
(4):将数组数字逆序输出
#include<stdio.h>
#include <string.h>
using namespace std;
const int N=10000001;//(1)
int main(){
char a[N],b[N];//(2)
scanf("%s",&a);
scanf("%s",&b);
int arr[N],brr[N],crr[N];//(3)
int len1=strlen(a);//(4)
int len2=strlen(b);//(5)
for(int i=0;i<len1;i++)
arr[i]=(a[len1-1-i]-'0');//(6)
for(int i=0;i<len2;i++)
brr[i]=(b[len2-1-i]-'0');//(7)
int max=len1;//(8)
if(len2>len1)
max=len2;
int t=0;
int k=0;//(9)
for(int i=0;i<max;i++){
if(i<len1)t+=arr[i];//(10)
if(i<len2)t+=brr[i];//(11)
crr[i]=t%10;//(12)
t/=10;//(13)
k++;
}
if(t)//(14)
crr[k++]=1;
for(int i=k-1;i>=0;i--)//(15)
printf("%d",crr[i]);
}
(1)设置一个足够大的数N,用于标识数组的长度
(2)创建两个字符数组用于存储高精度数字
(3)创建整形数组
(4)(5)求两个高精度数字的位数
(6)(7)将两个高精度数字逆序存储到整形数组中
(8)存储两个数字中长度更长的
(9)计算新数组的长度
(10)(11)将两个数字对应位置进行相加
(12)将相加得到的数字%10存储到数组中
(13)判断是否需要进1
(14)判断最后是否还需要进1
(15)逆序打印
高精度减法
主要思想:用字符数组进行接收数字,将数字逐一逆序存储到数组中,对应位置依次相减。做法和高精度加法类似。
小学减法的做法:
1.对应位置相减,不够相减就向后一位借1
高精度减法步骤:
(1):字符数组存储大数字
(2):逆序插入整形数组
(3):对应位置数字相减,并判断当前所在位的被减数是否需要借1
(4):将数组数字逆序打印
#include<stdio.h>
#include<string.h>
const int N=100001;//(1)
int cmp(int *arr,int*brr,int len1,int len2){//(10)
if(len1==len2)
for(int i=len1-1;i>=0;i--){
if(arr[i]!=brr[i])
return arr[i]>=brr[i];
}
else
return len1>=len2;
}
void sub(int *arr,int *brr,int*crr,int len1,int len2){//(11)
int t=0;
for(int i=0;i<len1;i++){
if(i<len1)t+=arr[i];//(12)
if(i<len2)t-=brr[i];//(13)
crr[i]=(t+10)%10;//(14)
if(t<0)//(15)
t=-1;
else
t=0;
}
}
int main(){
char a[N];//(2)
char b[N];//(3)
int arr[N];//(4)
int brr[N];//(5)
int crr[N];//(6)
scanf("%s",&a);
scanf("%s",&b);
int len1=strlen(a);
int len2=strlen(b);
for(int i=0;i<len1;i++)//(7)
arr[i]=(a[len1-i-1]-'0');
for(int i=0;i<len2;i++)//(8)
brr[i]=(b[len2-i-1]-'0');
int max=len1;//(9)
if(len2>len1)
max=len2;
//默认arr数组是大于brr数组的
if(cmp(arr,brr,len1,len2)){
sub(arr,brr,crr,len1,len2);
while(crr[max-1]==0&&max>1)//(16)
max--;
for(int i=max-1;i>=0;i--)//(18)
printf("%d",crr[i]);
}
else{
sub(brr,arr,crr,len2,len1);
while(crr[max-1]==0&&max>1)//(17)
max--;
printf("-");
for(int i=max-1;i>=0;i--)//(19)
printf("%d",crr[i]);
}
}
(1)设置一个足够大的数N,用于标识数组的长度
(2)(3)创建两个字符数组,用于接收高精度数字
(4)(5)创建两个整形数组,用于逆序存储高精度数字
(6)接收相减的结果
(7)(8)将大数字逆序插入到整形数组中
(9)比较两个高精度数字的长度,用于后面消除前导0
(10)比较两个高精度数字的大小
(11)模拟减法竖式运算
(12)(13)对应位置数字相减
(14)将相减得到的结果插入到数组中
(15)判断是否需要向后一位借1
(16)(17)去除前导0
(18)(19)逆序打印结果
高精度乘法
主要思想:依旧是模拟小学的乘法运算,使用字符数组存储大数字,再逆序存储到整形数组中。
小学乘法的做法:
1.对应位置相乘
2.对相乘的结果%10加到后一位
这里我们进行乘法的模拟运算:
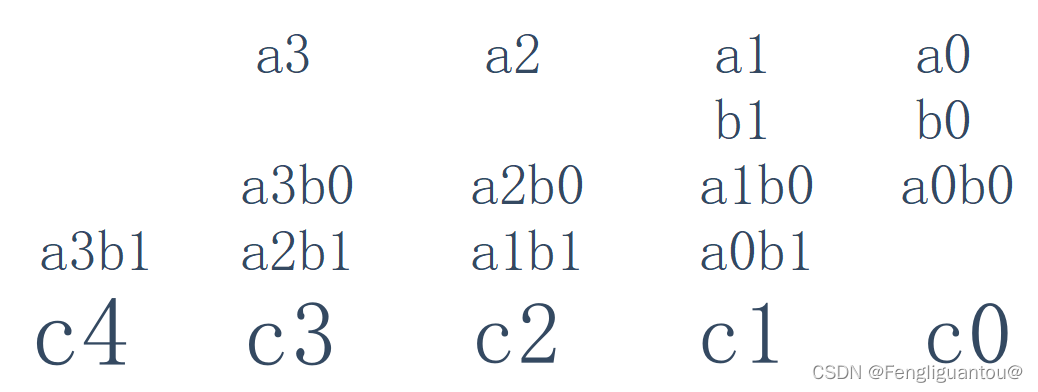
通过该图我们发现:
a0b0对应C1的位置
a1b0对应C1的位置
a2b0对应C2的位置
a3b0对应C3的位置
a0b1对应C1的位置
a1b1对应C2的位置
a2b1对应C3的位置
a3b1对应C4的位置
由此可以归纳出来一个规律
C[i+j]=a[i]*a[j]
由此也可得出进位等于C[i+j+1]
高精度乘法的步骤:
(1):字符数组存储大数字
(2):逆序插入整形数组
(3):对应位置数字相乘,相乘结果进行%10运算,并加到后一位上。
(4):将数组数字逆序打印
#include<stdio.h>
#include<string.h>
const int N=100001;//(1)
int main(){
char a[N];//(2)
char b[N];//(3)
int arr[N];//(4)
int brr[N];//(5)
int crr[2*N];//(6)
scanf("%s",&a);
scanf("%s",&b);
int len1=strlen(a);
int len2=strlen(b);
for(int i=0;i<len1;i++){//(7)
arr[i]=(a[len1-1-i]-'0');
}
for(int i=0;i<len2;i++){//(8)
brr[i]=(b[len2-1-i]-'0');
}//将数字逆序插入到数组中
for(int i=0;i<len1;i++){
for(int j=0;j<len2;j++){
crr[i+j]+=arr[i]*brr[j];
crr[i+j+1]+=crr[i+j]/10;//(9)
crr[i+j]%=10;//(10)
}
}
int len3=len2+len1;
while(crr[len3-1]==0&&len3>1)//(11)
len3--;
for(int i=len3-1;i>=0;i--){//(12)
printf("%d",crr[i]);
}
}
(1)设置一个足够大的数N,用于标识数组的长度。
(2)(3)创建两个字符数组用于存储高精度数字。
(4)(5)(6)创建整形数组。
(7)(8)将数字逆序插入数组中
(9)对所得结果%10进行进位操作
(10)相乘得到的结果需要进行%10才能存储到数组中
(11)去除前导0
(12)逆序打印数字
高精度除法
主要思想:依旧是模拟小学的除法运算,使用字符数组存储大数字,再存储到整形数组中。(这里插入到数组中,不是逆序插入!)
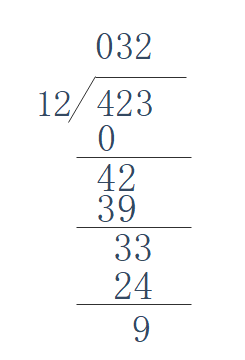
(1)4/12不够除,所以第一位商0
(2)42/12商3余3
(3)33/12商2余9
所以答案就为32余9
这里的过程为:
4/12,不够除
410+12=42 ,42/12=3,这位余下了一个3
310+3==33 , 33/12=2,被除数每一位都走完,除法结束。余数为0
可以得到规律:
前一位的余数*10+当前位的数字/除数=商
高精度除法步骤:
(1):字符数组存储大数字
(2):正序插入整形数组
(3):计算上一位的余数*10+当前位的数字/除数的结果
(4):计算当前位的余数
(5):将数组数字逆序打印
#include<stdio.h>
const int N=10000001;//(1)
#include<string.h>
int main(){
char a[N];//(2)
int arr[N];//(3)
int brr[N];//(4)
int b;//(5)
scanf("%s",&a);
scanf("%d",&b);
int len=strlen(a);
for(int i=0;i<len;i++){//(6)
arr[i]=(a[i]-'0');
}
int t=0;//(7)
for(int i=0;i<len;i++){
brr[i]=(t*10+arr[i])/b;//(8)
t=(t*10+arr[i])%b;//(9)
}
int lenc=0;
while(brr[lenc]==0&&lenc<len-1&&len>1){//(10)
lenc++;
}
for(int i=lenc;i<len;i++)//(11)
printf("%d",brr[i]);
printf("\n");
printf("%d",t);
}
(1)创建一个足够大的N为数组分配空间
(2)创建一个字符串数组用于存储大数字
(3)(4)创建两个整形数组,一个用于存储大数字,一个用于存储结果
(5)存储低精度数字
(6)将大数字按正常顺序存储数组中
(7)因为是第一位,没有上一位,所以余数t一开始设置为0
(8)当前位的数字加上上一位的余数*10,再除以除数
(9)计算当前位的余数
(10)去除前导0
(11)顺序打印结果
博主最近开通了个人的公众号,会持续更新C/C++方向的计算机知识,有需要的小伙伴欢迎订阅。

