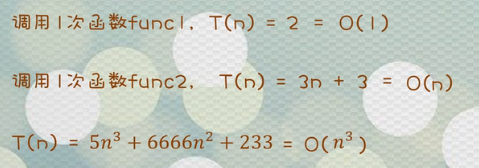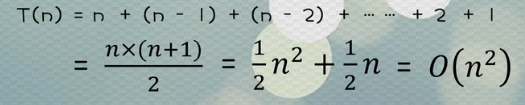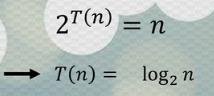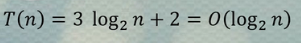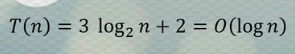1. 时间复杂度分析
1.1 概述
试分析如下两个方法,分别执行了多少次?
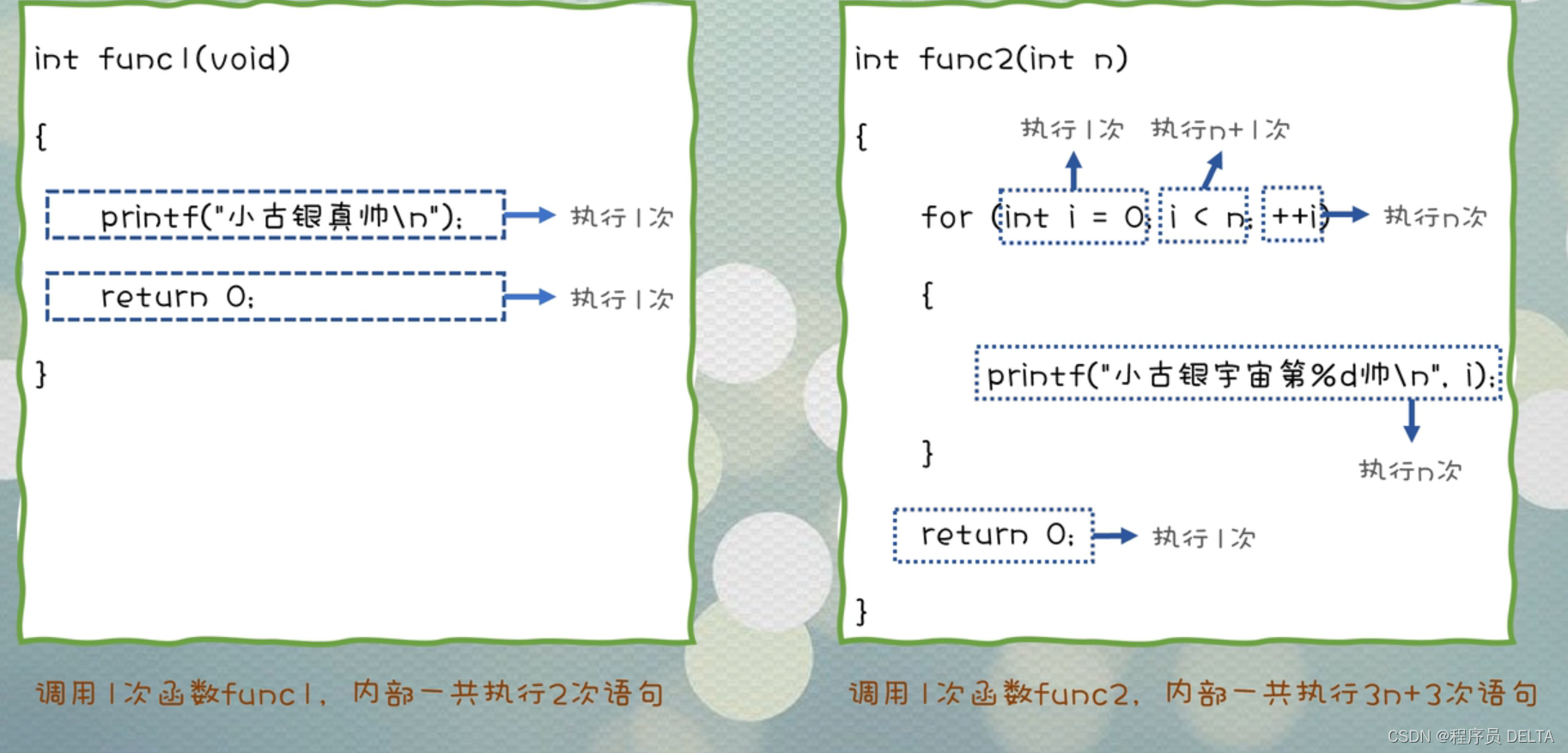
分析:
func2里的i < n执行了n+1次,因为包括一次不通过的判断
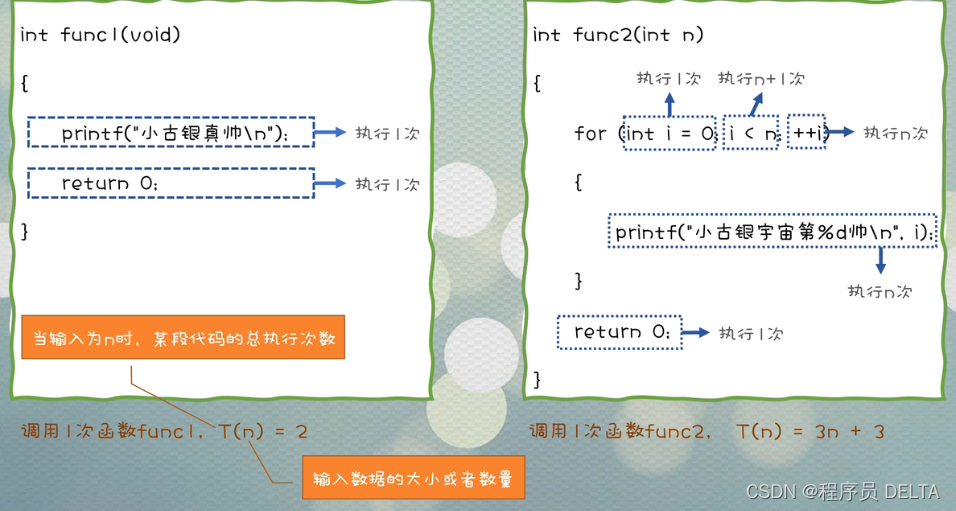
说明:
为了方便我们的书写表达,我们一般使用T(n)表示程序的总执行次数,n是输入数据的大小或输入数据的数量,T是当输入数据为n时,某段代码的总执行次数。
问题说明:
????????作为衡量代码的执行速度的依据,当代码比较多的时候,使用T(n)就有点麻烦了,我们还需要一条条语句去数,而且函数调用函数的时候,运算起来也很麻烦。所以算法一般使用T(n)简化的估算值,来衡量代码执行的速度。这个简化的估算值叫做时间复杂度。
1.2 根据T(n)得出时间复杂度
结论1:
????????当T(n)的值为:常数,那么时间复杂度可以直接估算为1。

结论2:
????????当T(n)的值为:常数*n + 常数,那么时间复杂度的计算为:
- 去掉常数项,因为随着n的增大,第一部分的值不断变大,而第二部分对于第一部分无任何影响
- 去掉第一部分的系数,或者理解为将第一部分常数估算为1

结论3:
????????当T(n)的值为:多项式,那么时间复杂度的计算为:
- 保留n的最高次项,因为随着n的增大,后面的项远远不如最高次项的增长大,所以可以直接省略低次项
- 去掉最高次项的系数

补充:
上诉表示的时间复杂度并不完整,我们还需要加上大写字母O,也叫大O表示法
总结:
1.3 常见代码的时间复杂度
说明:
为了更快求出时间复杂度,我们需要学习一些常见代码的时间复杂度
案例1:
没有循环、没有判断,只有一条条的语句
案例2:
只有一重循环
案例3:
多重循环
说明:
printf()本身执行一次,但是在里层循环的作用下,执行了1*n次,然后在外层循环的作用下,整体执行了(1*n)*n次
案例4:
多个循环
说明:
我们需要以运行时间最长的循环作为时间复杂度的依据
所以时间复杂度取n的最高次幂
案例5:
存在if判断语句
还是以运行时间最长的循环作为时间复杂度的依据
所以时间复杂度取n的最高次幂
1.4 常见且特别代码的时间复杂度
案例1:
分析:
此案例中内循环的条件在不断变化,每当 i 增加1,里层循环就会少执行1次。
将每个执行次数相加可得出总执行次数的不精确结果!
最后得出的时间复杂度结果为:
案例2:
分析:
此案例中 i 每次都成2倍的变化,我们先假设 n = 8 和 n = 16 进行讨论:
- 通过假设能够得出printf()的执行次数为3和4
- 3和4只是printf()执行的次数,完整的次数应加上判断,相乘,初始化的次数
- 在简化成时间复杂度的时候,都会省略掉
- 对执行次数主要的影响来源于 i *= 2,通过观察可以发现:
- 通过对数法则可得T(n):
- 不过上面只是统计了printf的次数,写完整一点:
- 由于时间复杂度需要去掉系数和常数,所以时间复杂度为:
- 最后对数的底数和系数是一样的,也需要去掉,所以最后的结果为:
2. 时间复杂度的速度(重要!)
说明:时间复杂度使用来描述一个算法的快慢程度的,所以我们有必要了解时间复杂度的速度
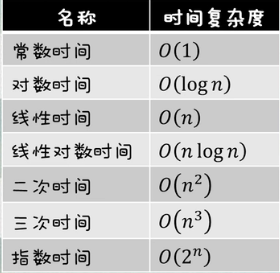
2.1 常见的时间复杂度
说明:
横坐标代表数据大小或数量,纵坐标代表时间复杂度
通过图示能够发现随着数据量增大,时间复杂度呈现何种变化
1)对比:O(1)和O(log n)的变化
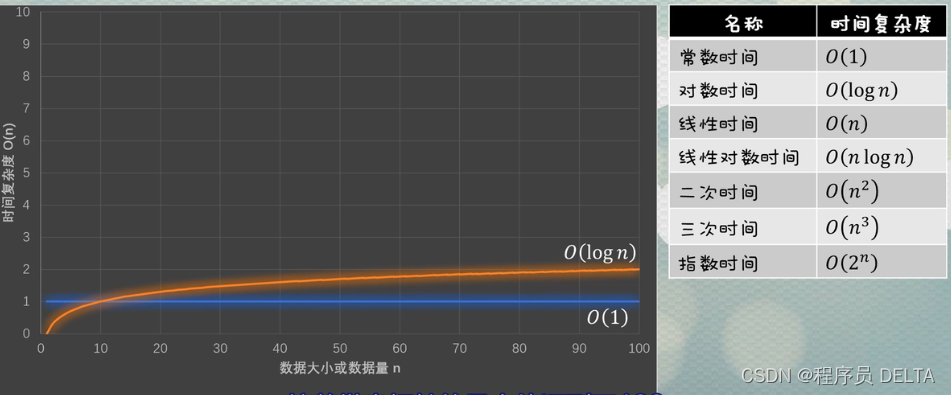
2)对比:O(n)和O(nlog n)和O(n2)的变化
将纵坐标放大到100
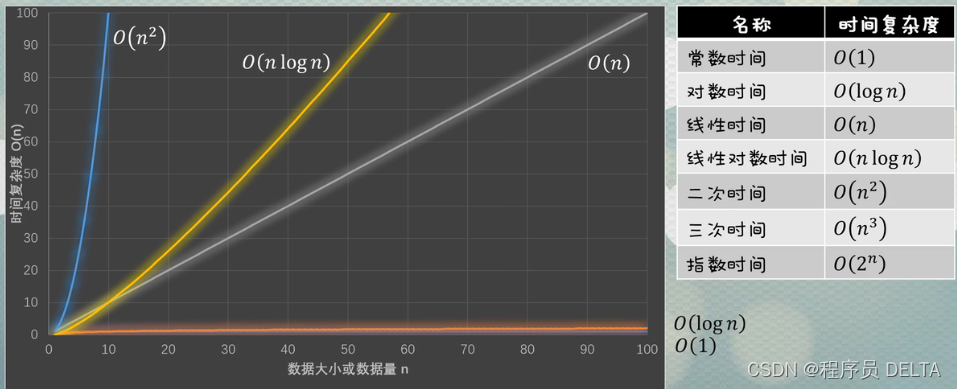
3)对比:O(n2)和O(n3)和O(2n)的变化
将纵坐标放大到10000
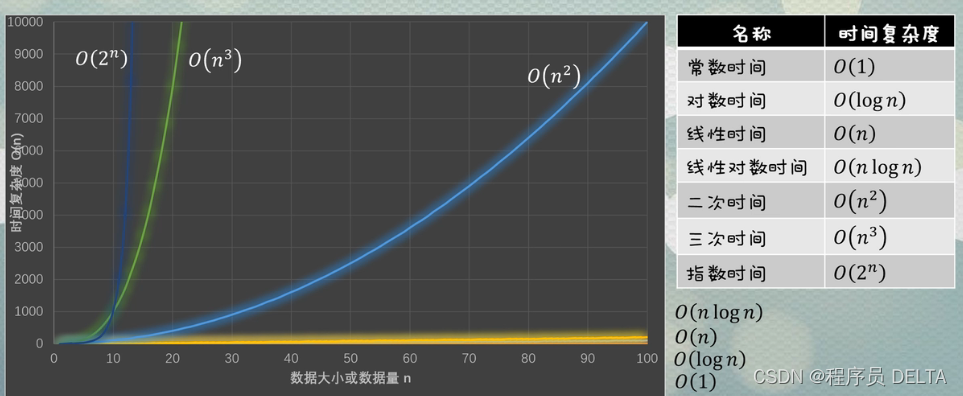
总结:上诉时间复杂度时间进行排序(由快到慢)
2.2 拓展
2015年NOIP普及组题目