3.1栈(stack)
3.1.1栈的基本概念
定义

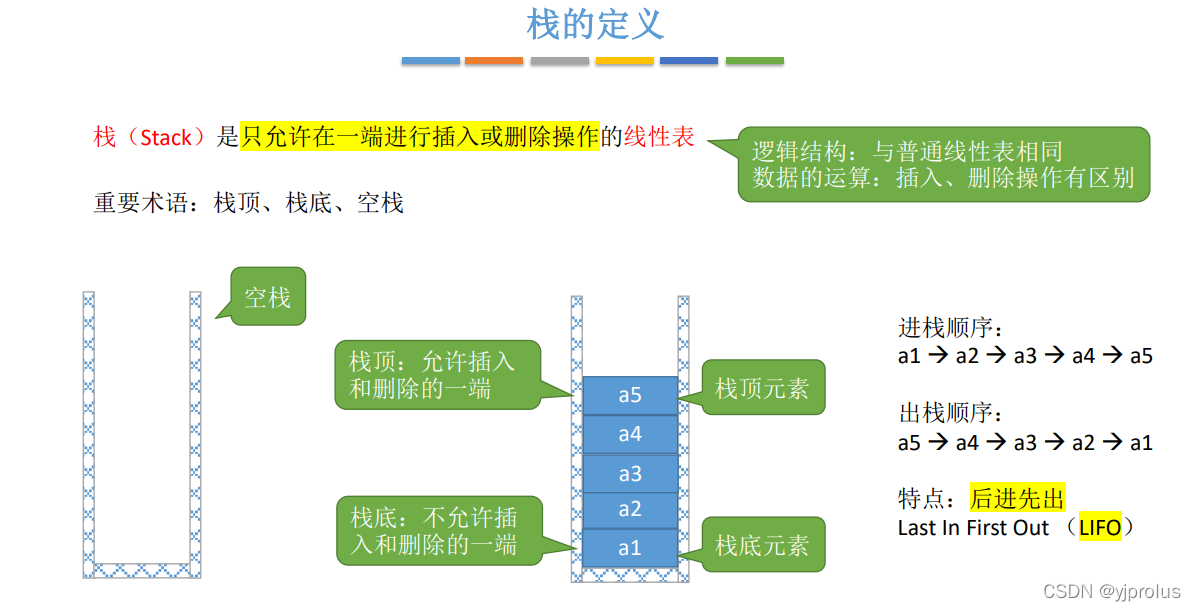
基本操作


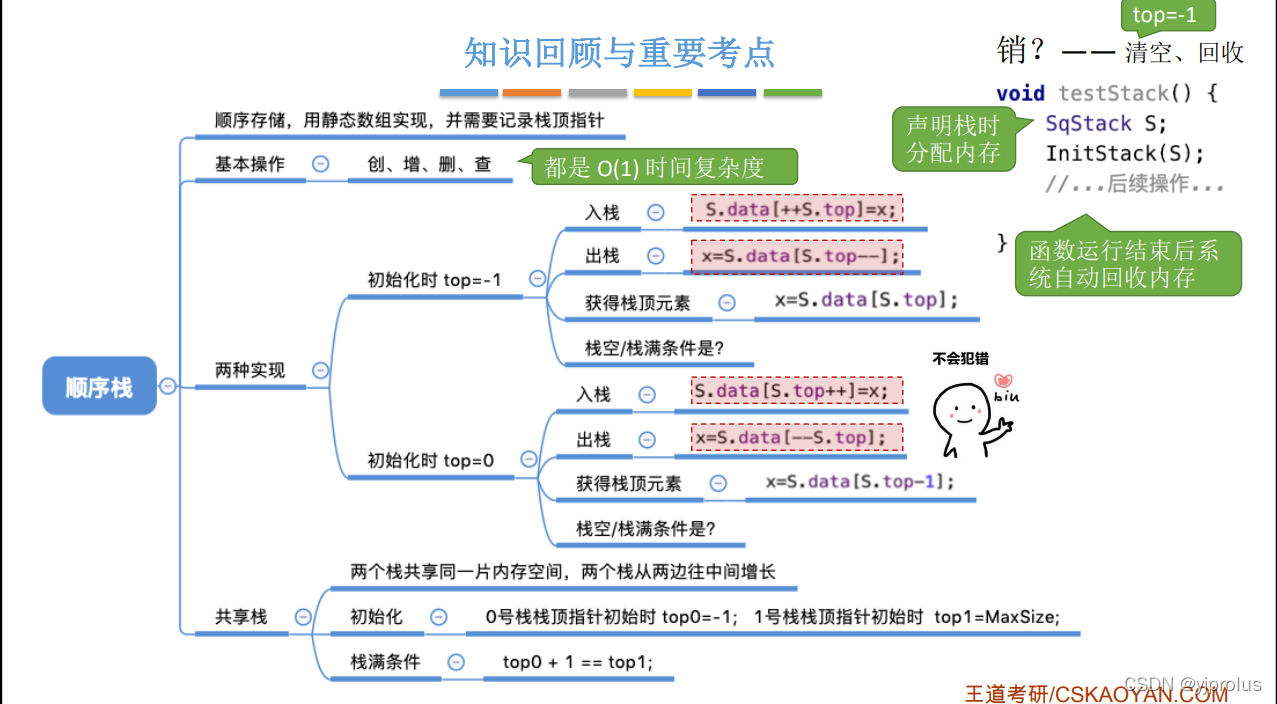
3.1.2 栈的顺序存储
初始化

进栈操作
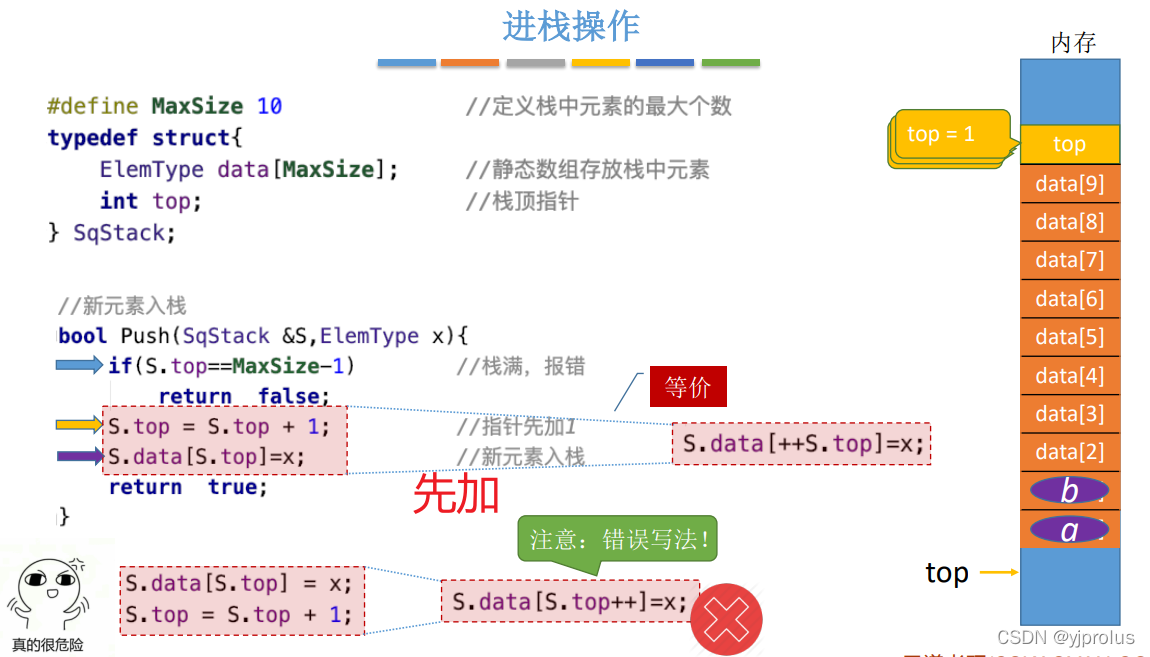
出栈操作

读栈顶元素操作

另一种表示方式(top=0)
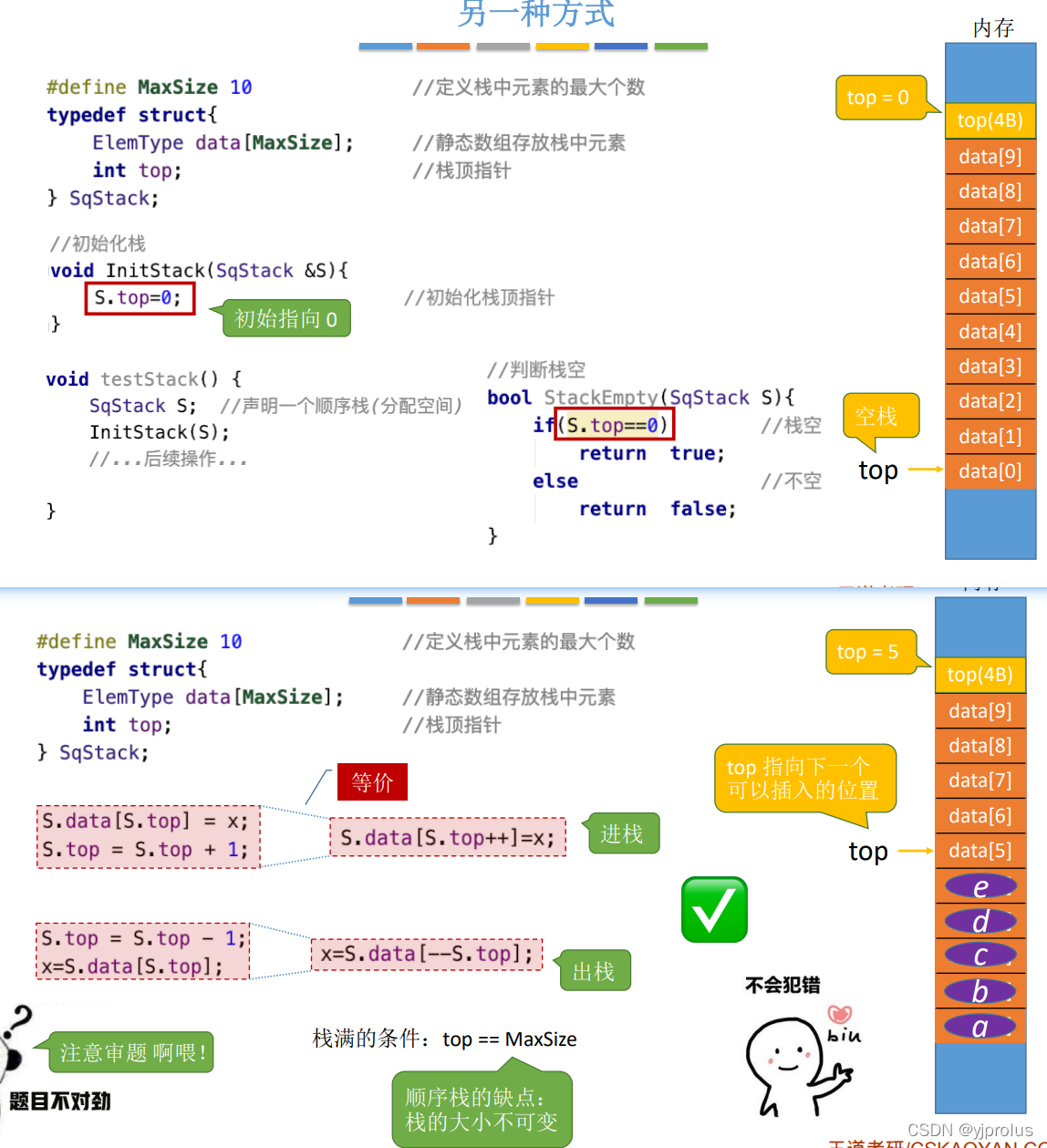
共享栈

总结
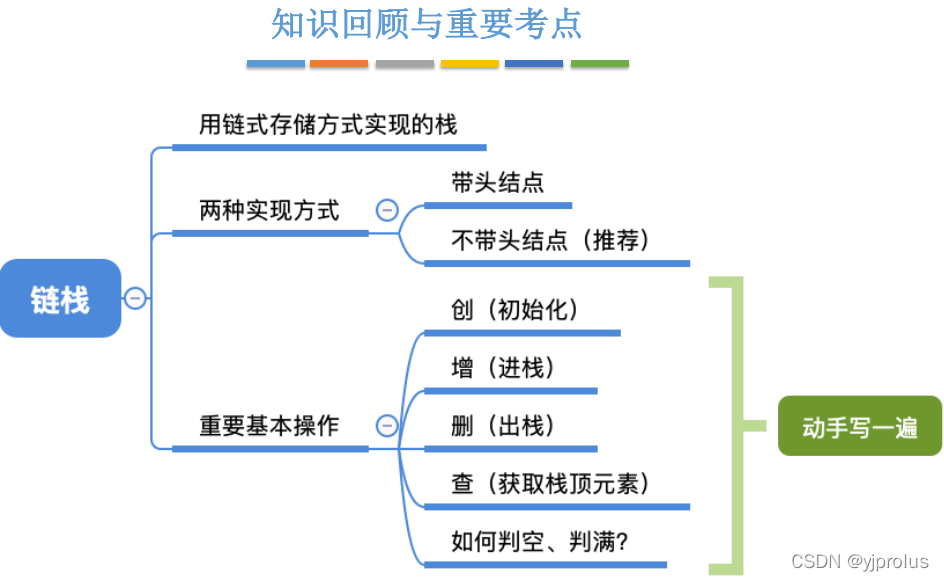
3.1.3栈的链式存储
进栈(头插法建立单链表)

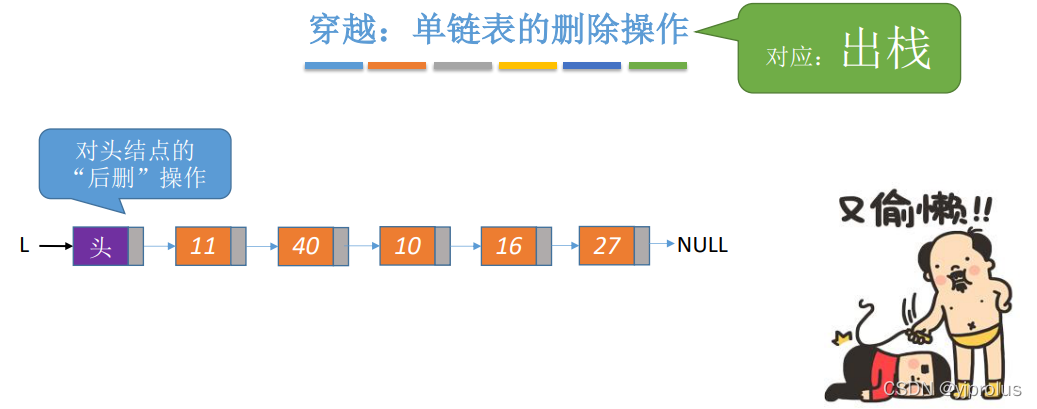
出栈(对头结点的“后删”操作)
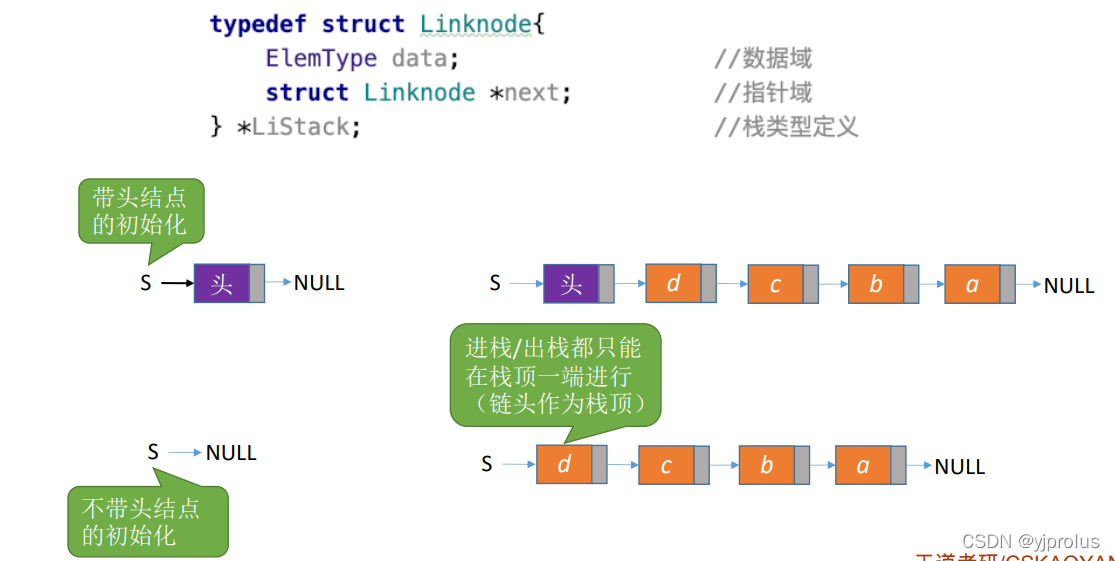
链栈的定义
总结
3.2队列(Queue)
3.2.1队列的基本概念
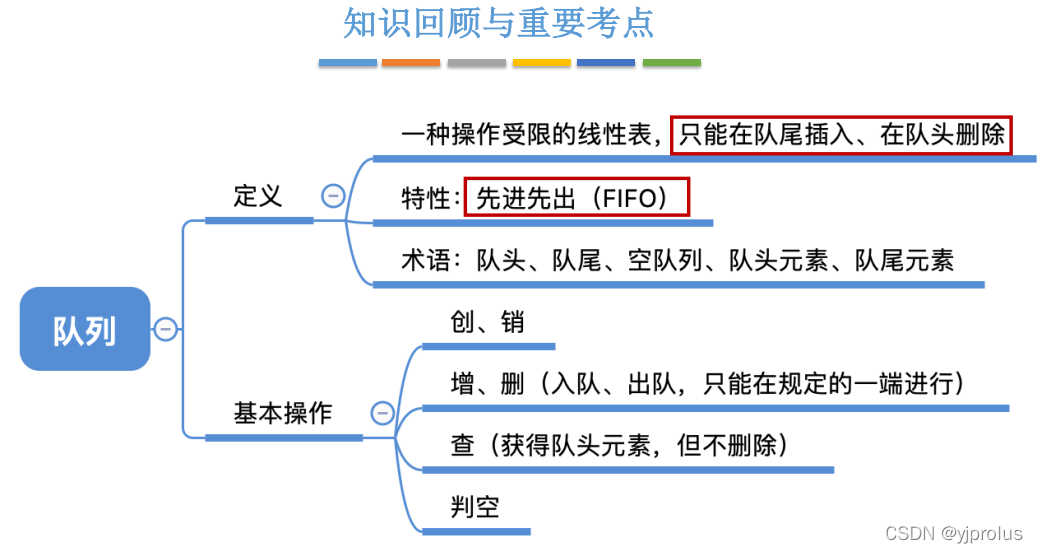
定义
队列(Queue)是只允许在一端进行插入,在另一端删除的线性表
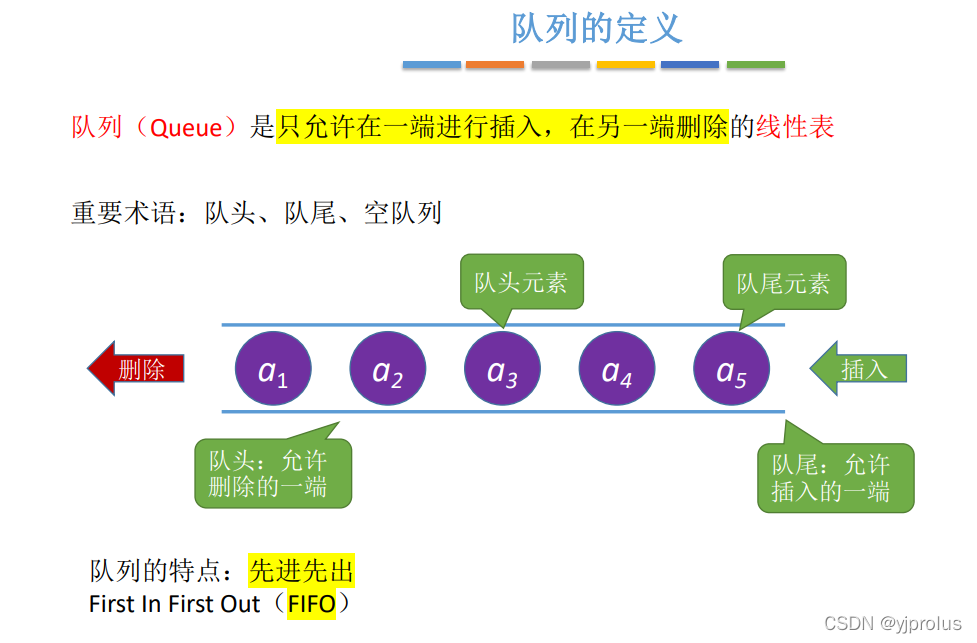
基本操作

总结
3.2.2队列的顺序存储结构
初始化

入队操作(只能作为队尾插入)
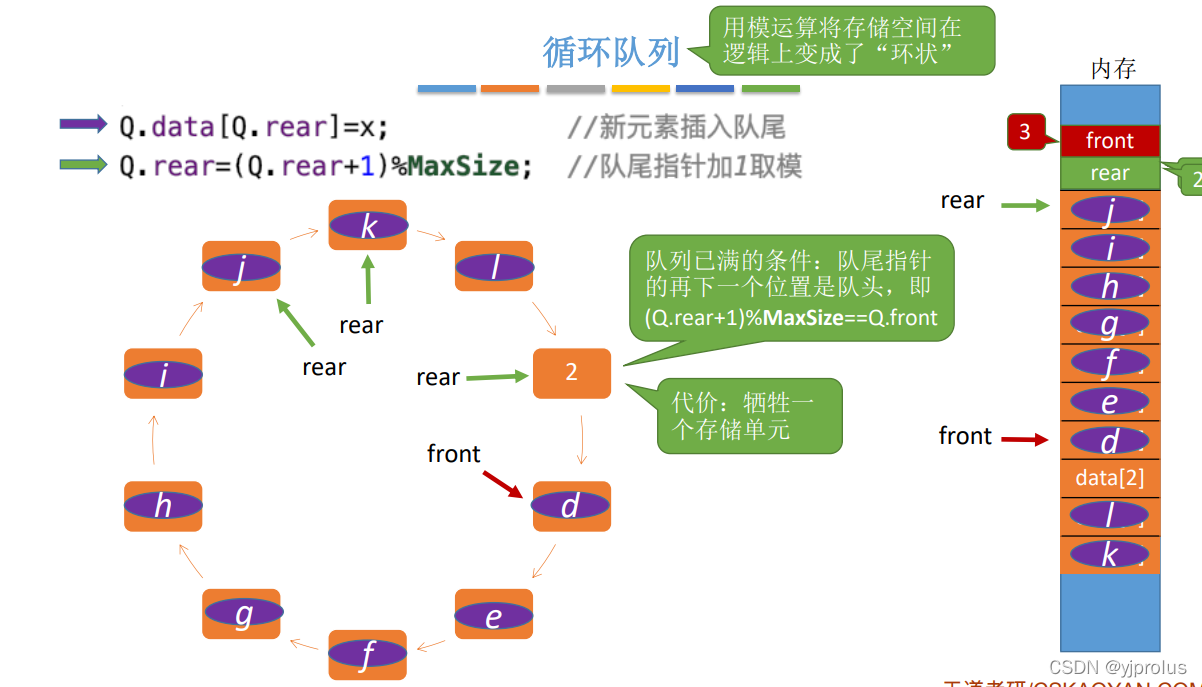
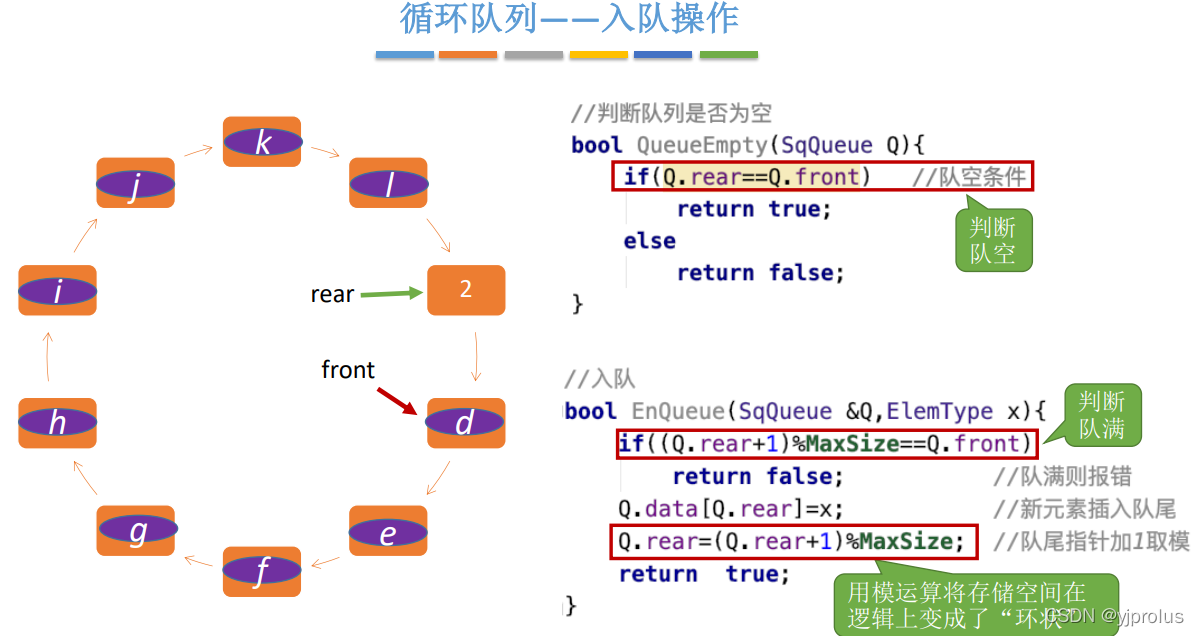
出队操作
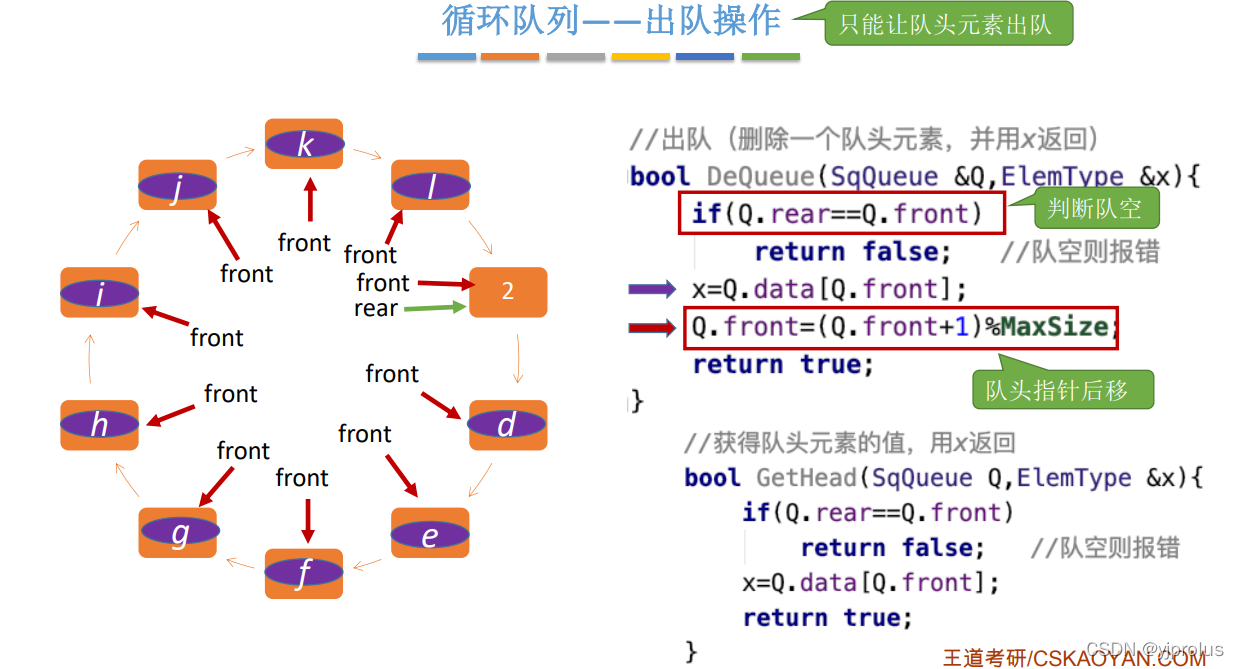
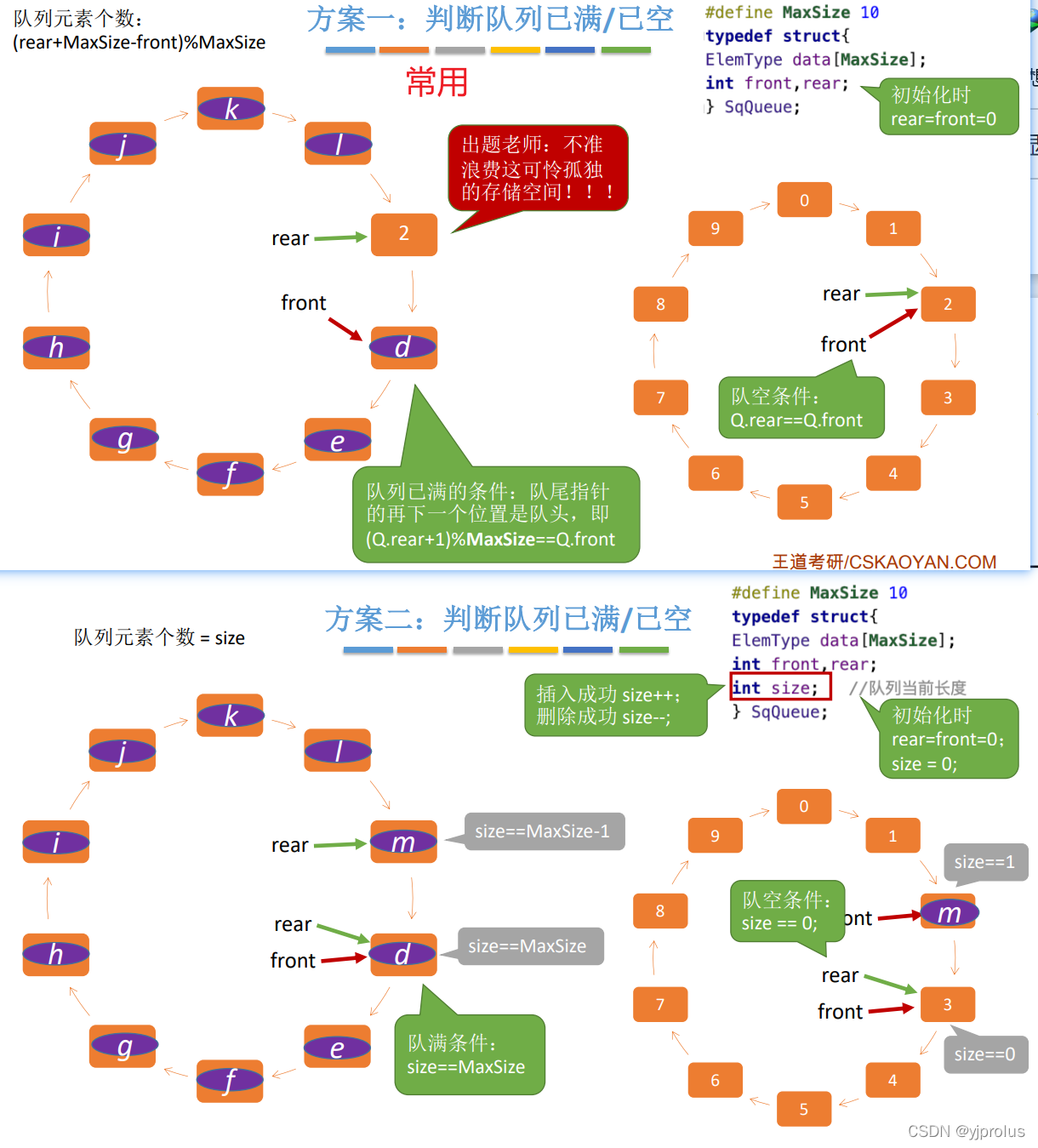
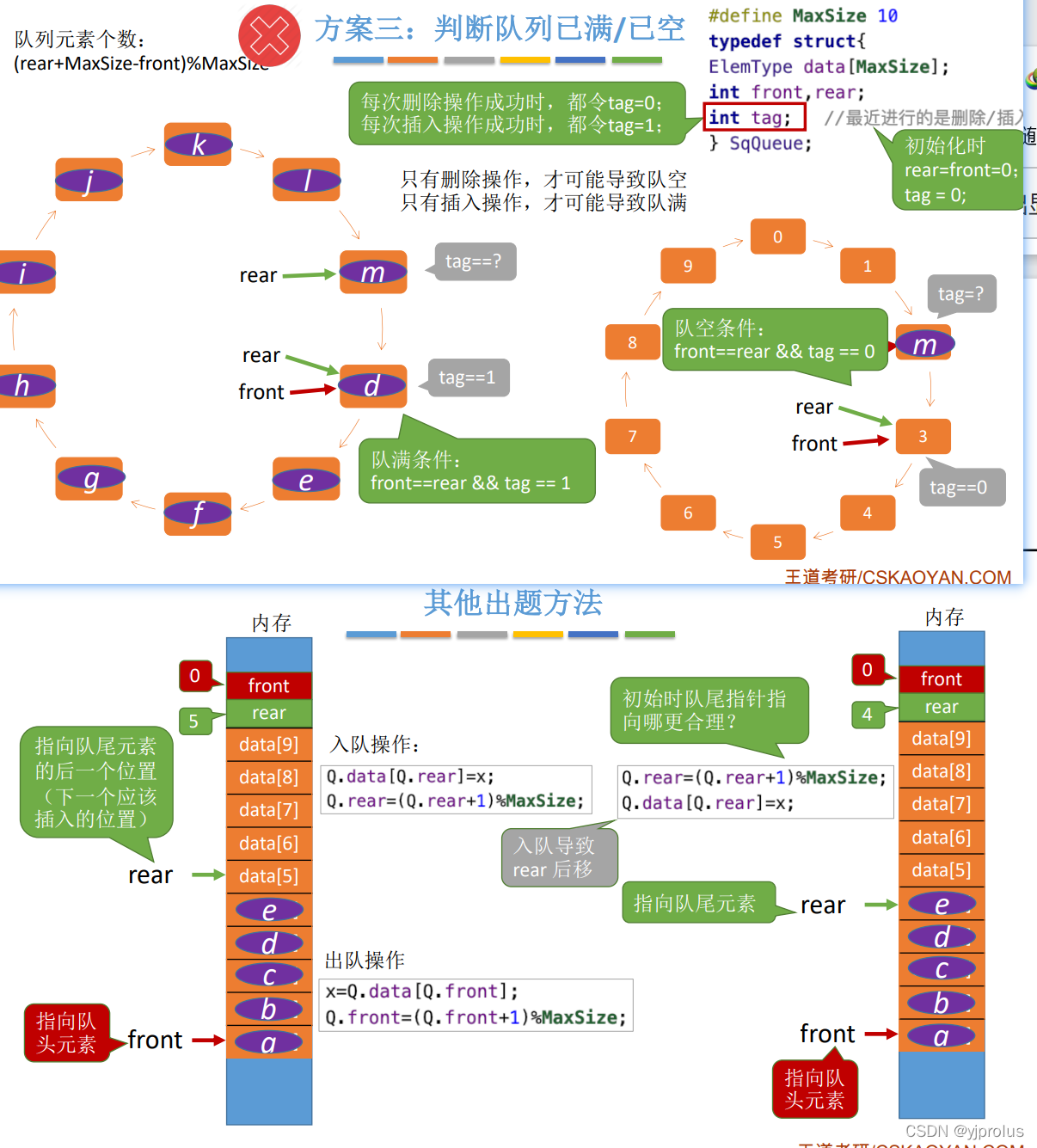
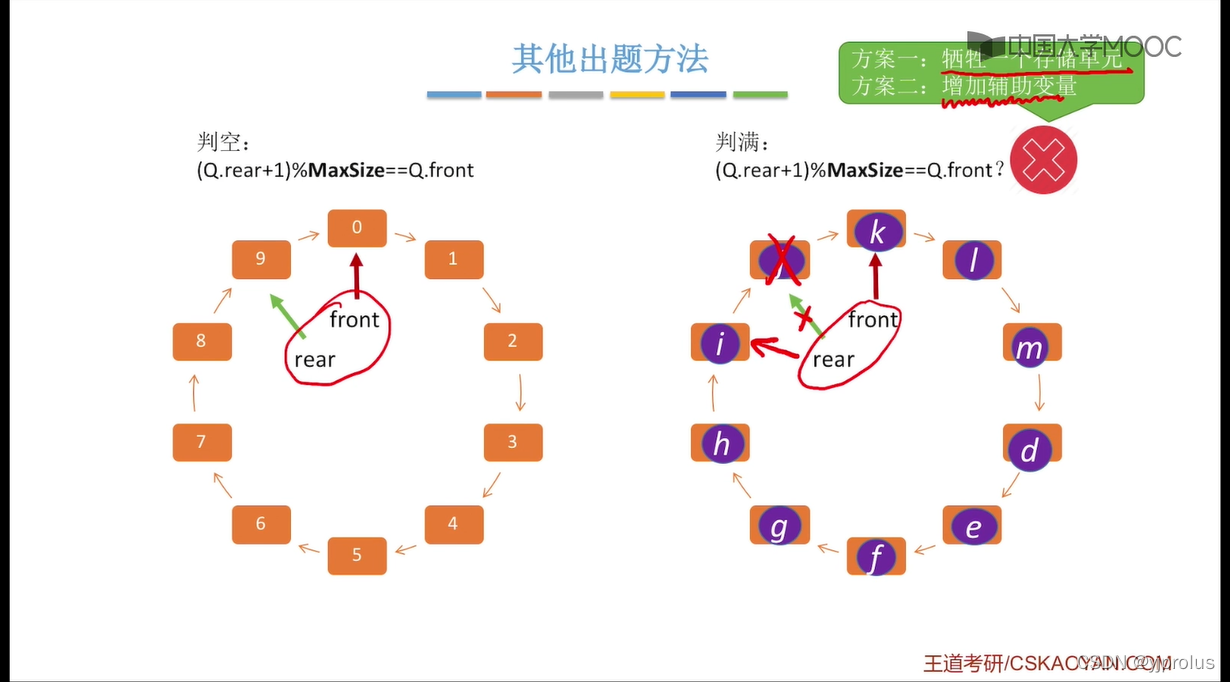
判断队列满/空的方法
3.2.3队列的链式存储结构
初始化(带头结点)

初始化(不带头结点)
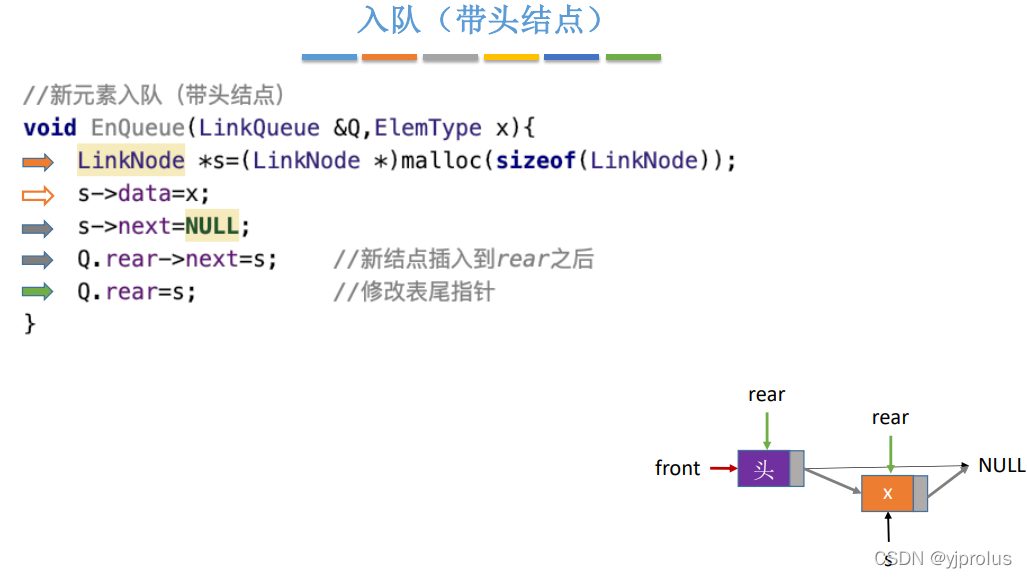
入队(带头结点)
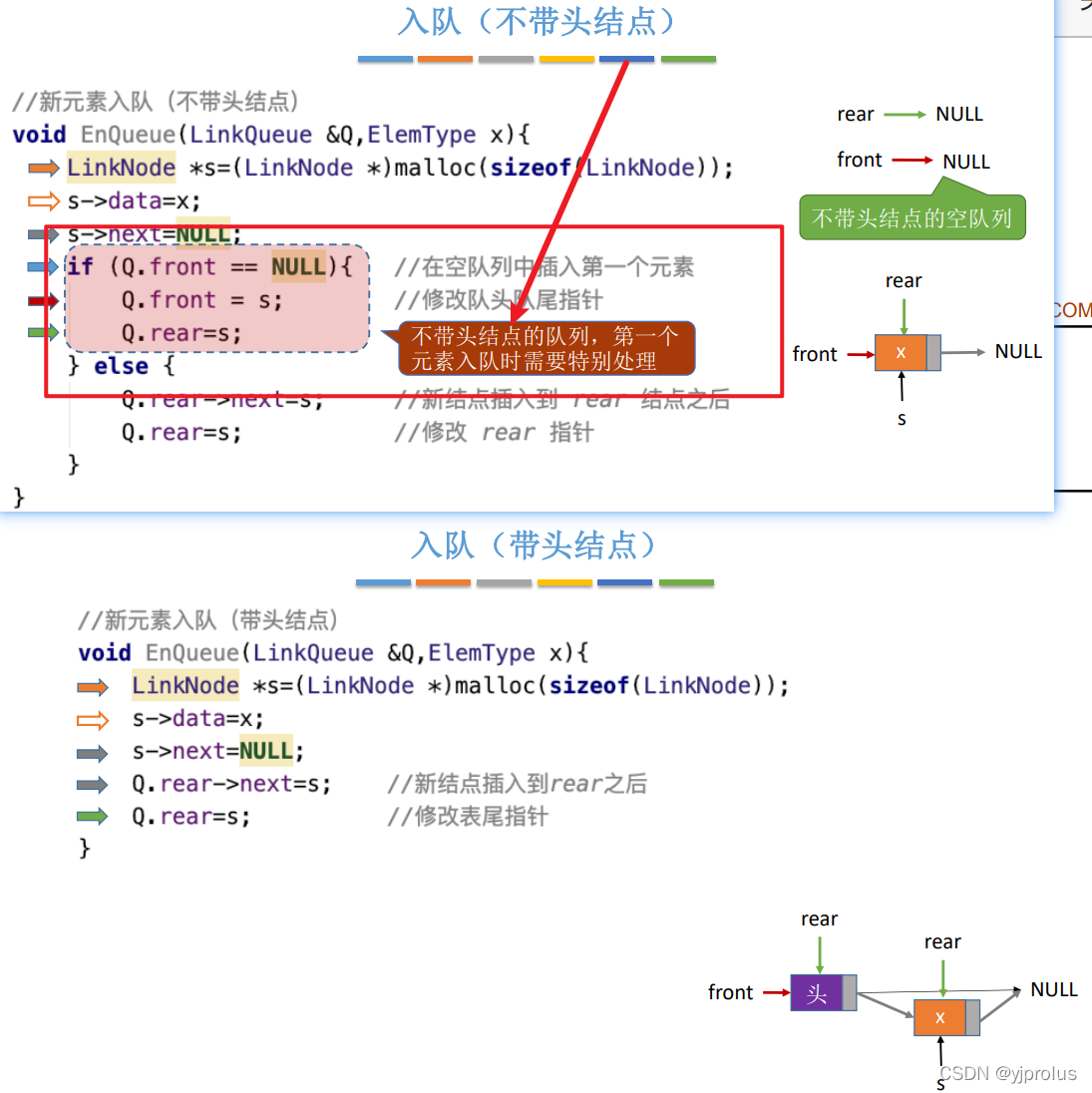
入队(不带&带头结点)
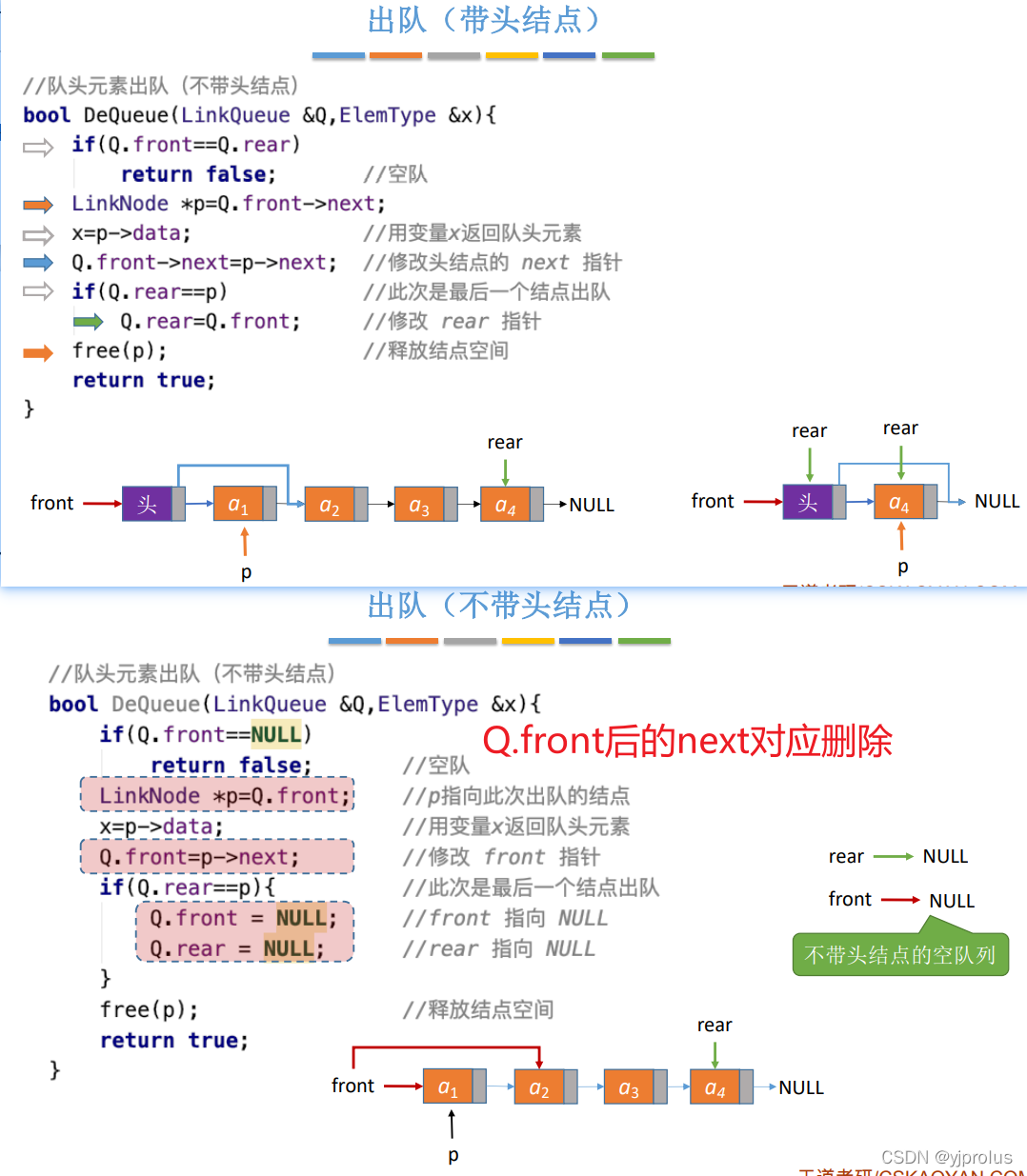
出队(带&不带头结点)
队满的条件
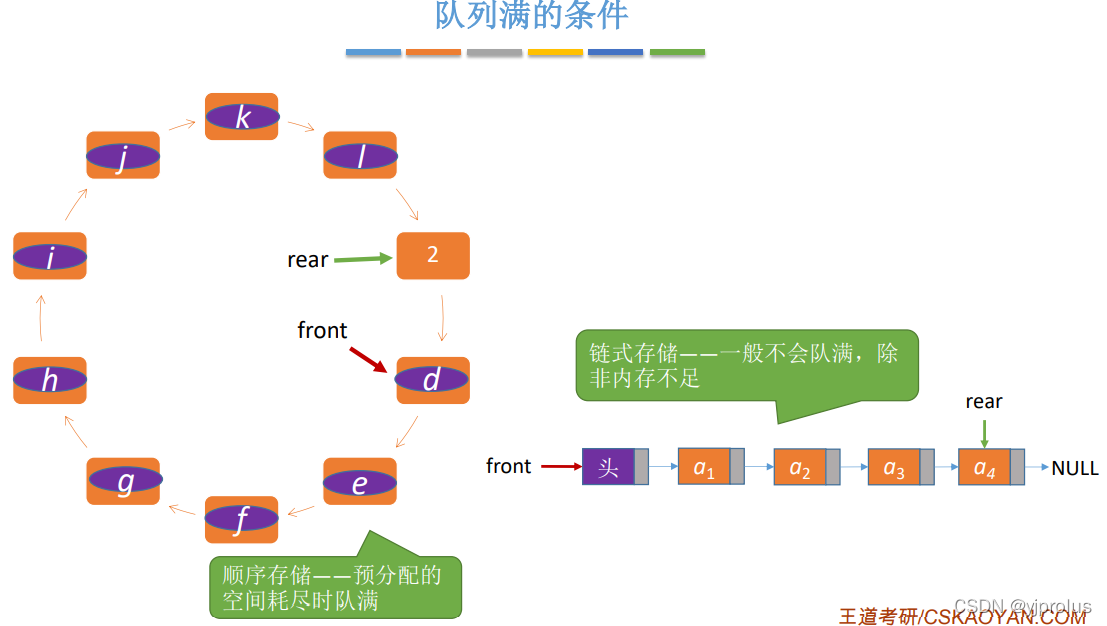
总结
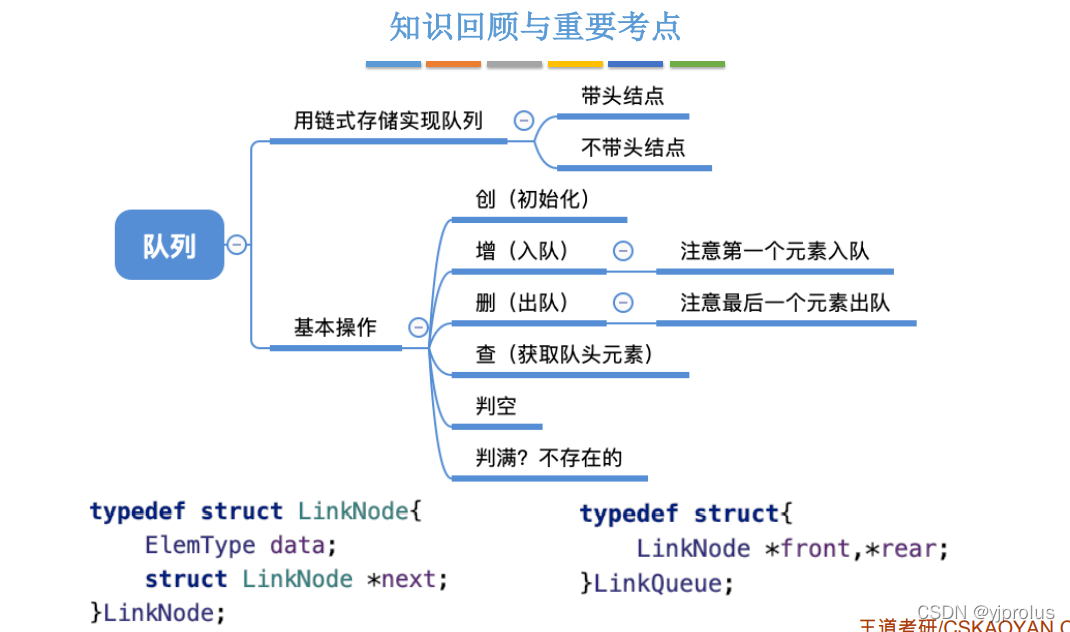
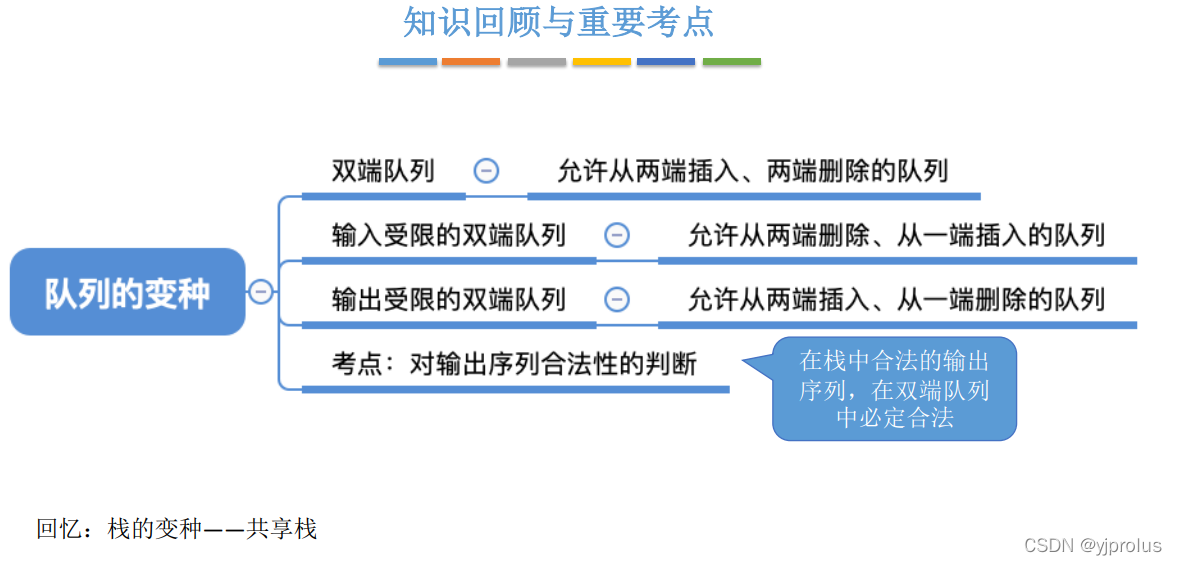
3.2.4双端队列
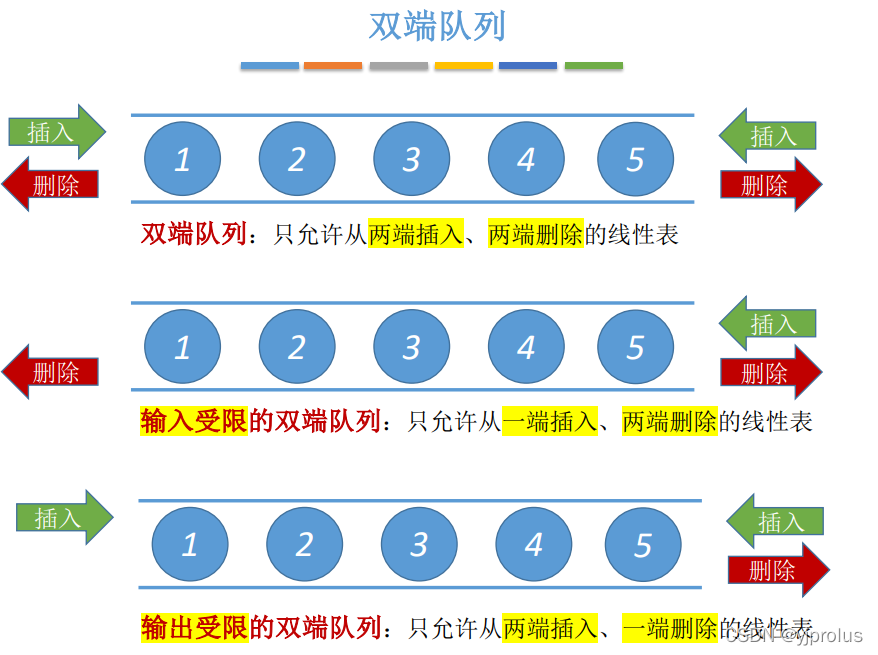
考点:判断输出序列合法性
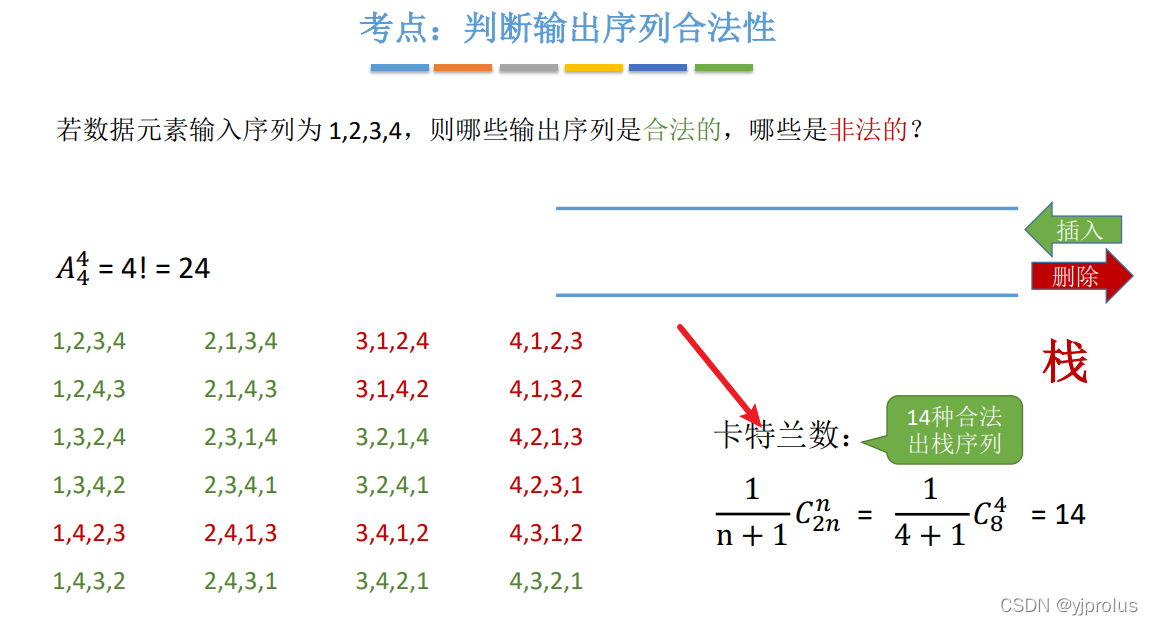
栈中合法的序列,双端队列中一定也合法
总结
3.3栈的应用
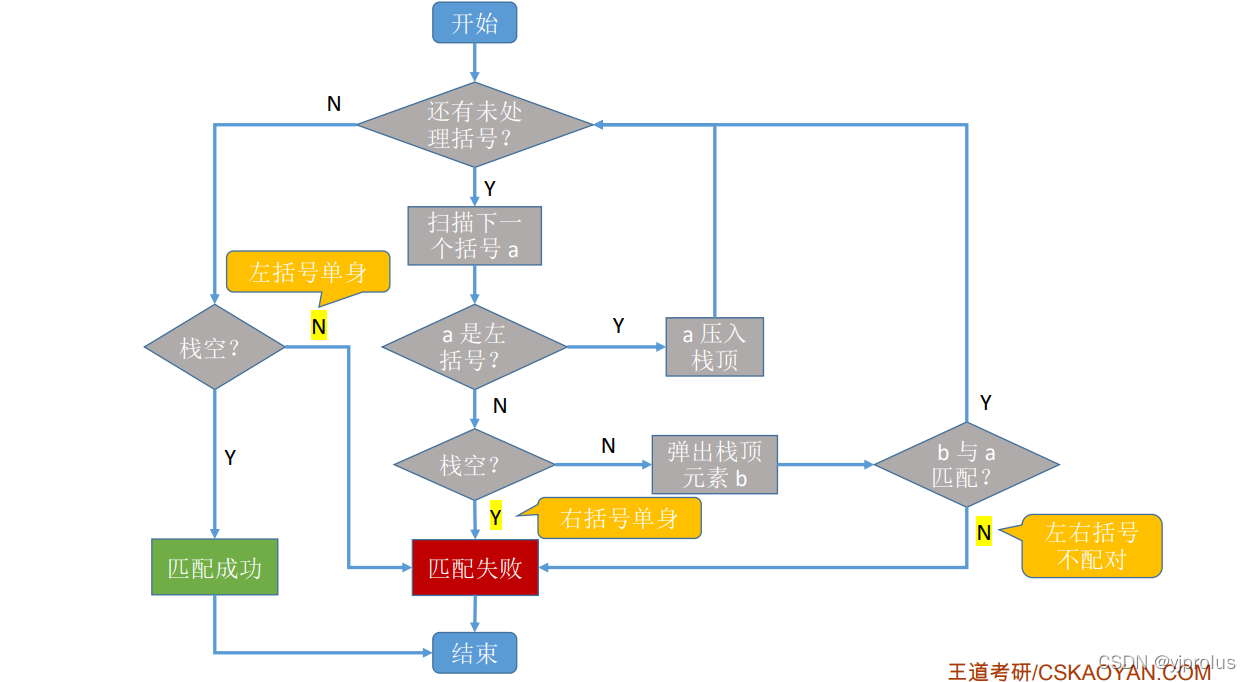
3.3.1栈在括号匹配中的应用
原理:遇到左括号就入栈;遇到右括号,就 “消耗”一个左括号。

流程图
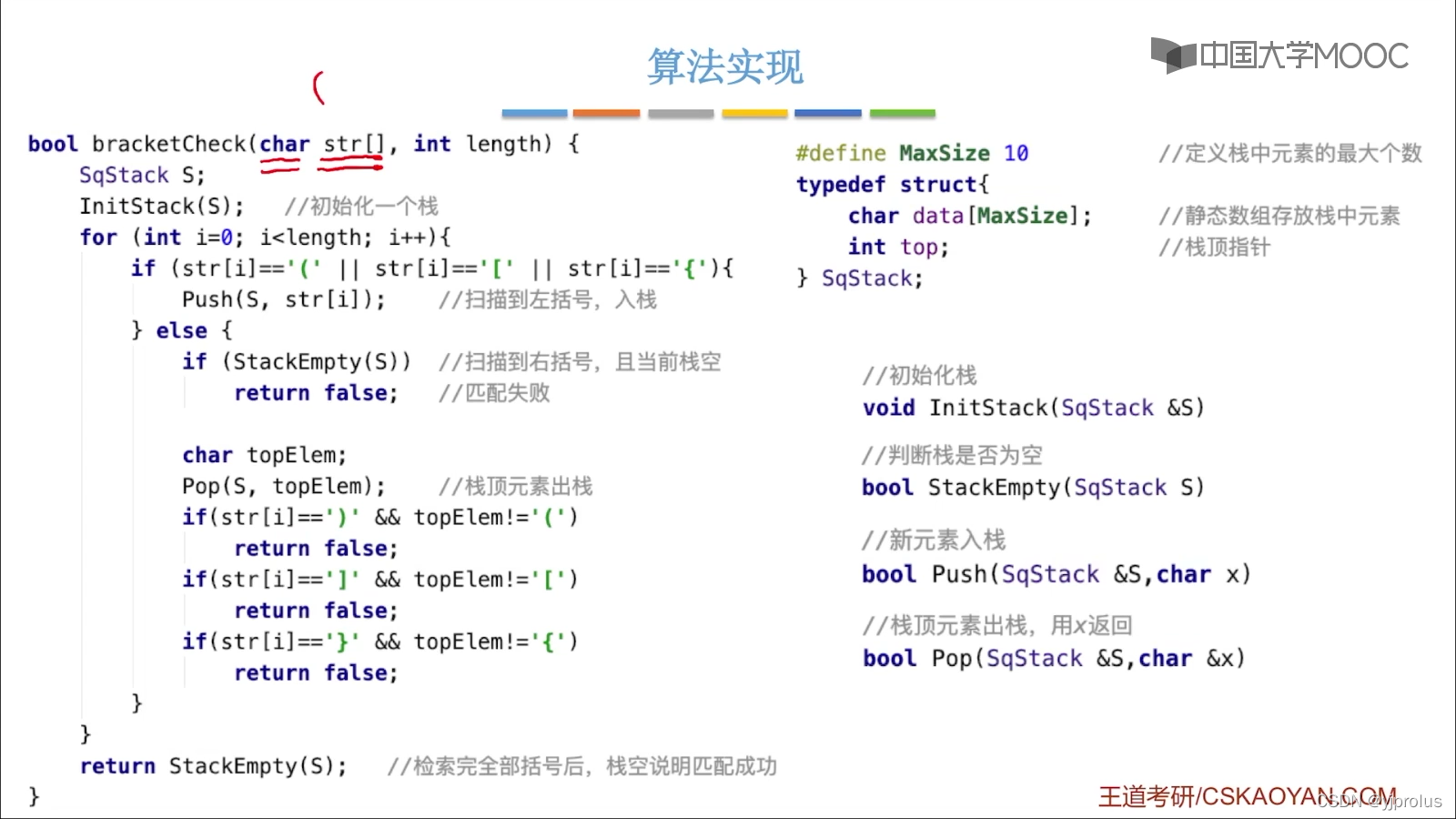
代码
总结

3.3.2栈在表达式求值中的应用

//TODO
3.3.3栈在递归中的应用
函数调用背后的过程
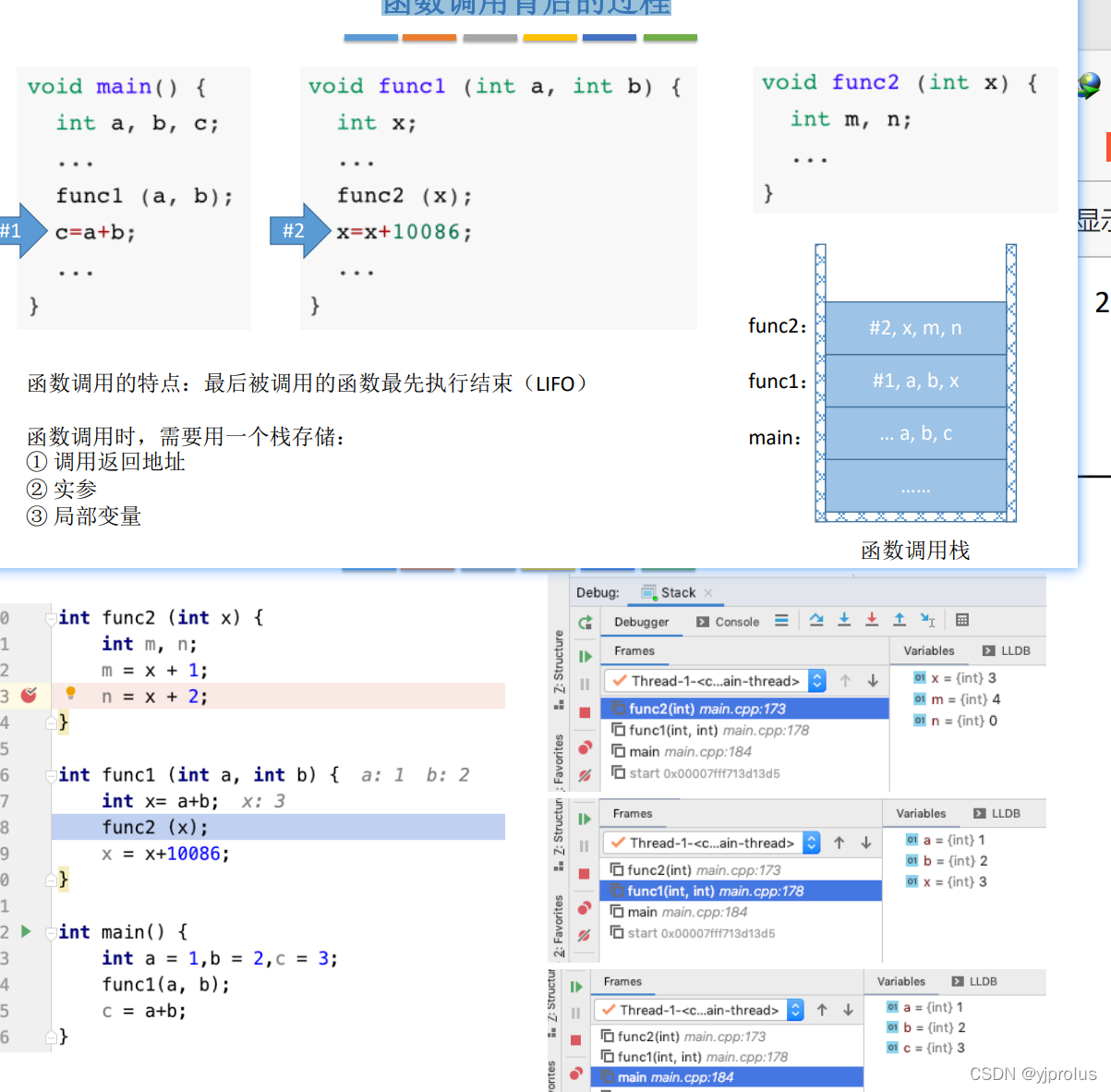
栈在递归中的应用

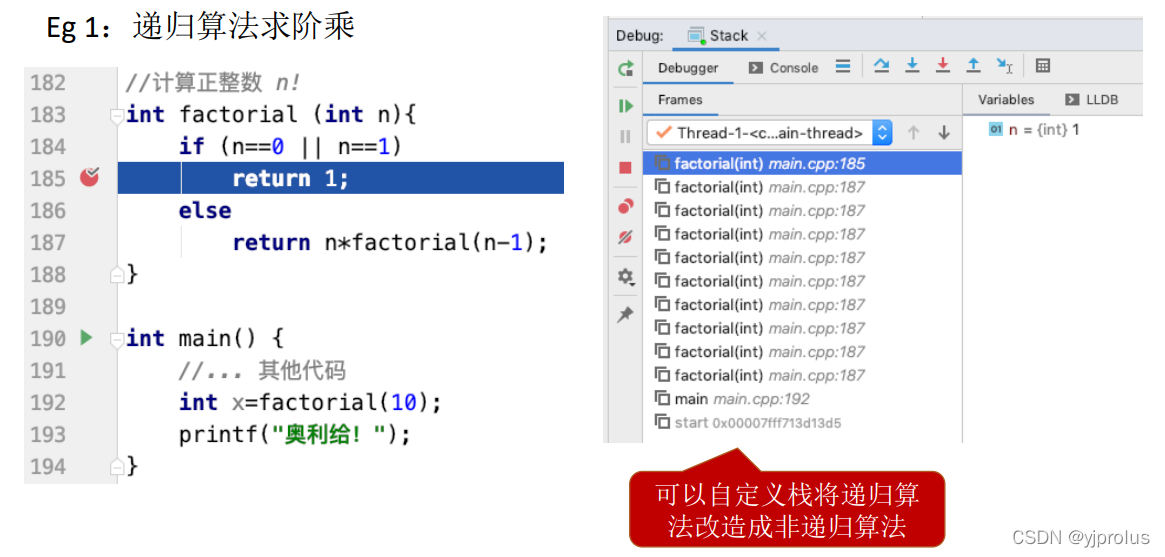
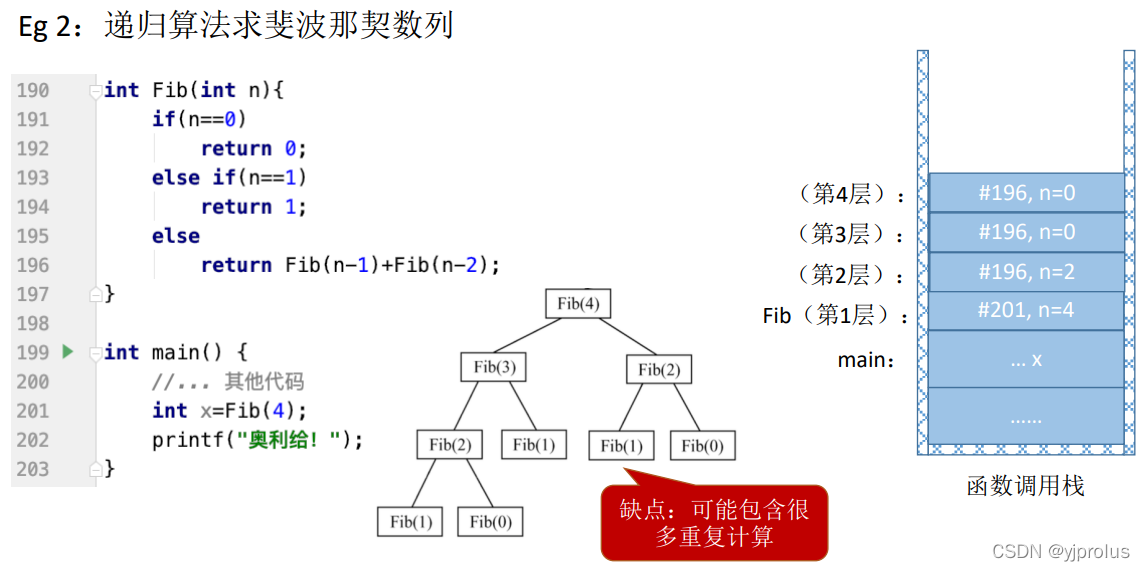
总结

3.4特殊矩阵的压缩存储
数组的存储结构

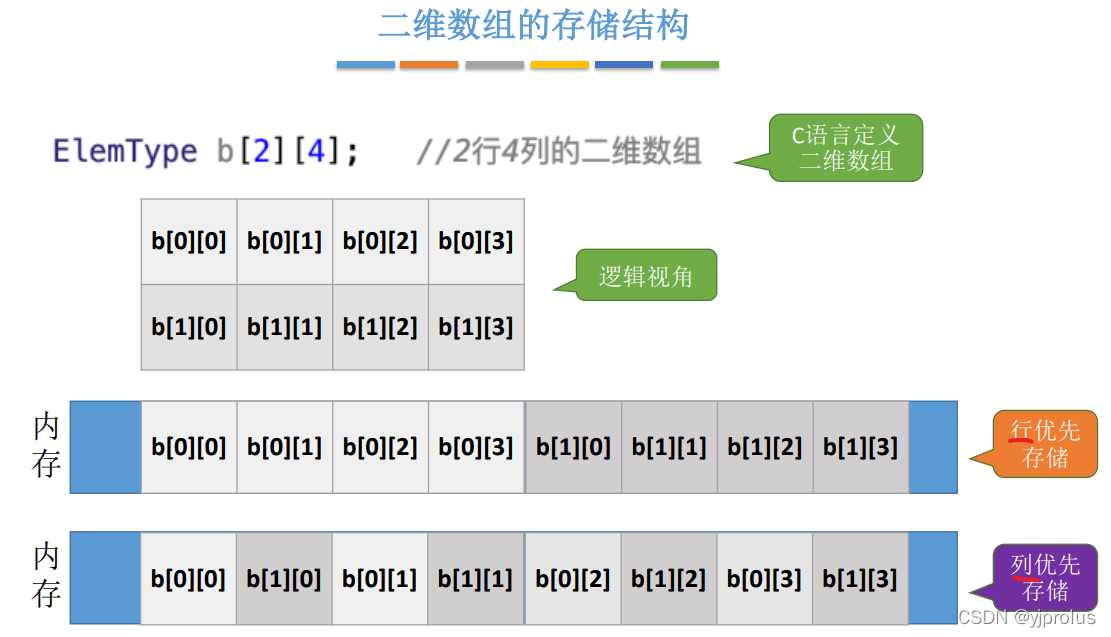
- M行N列的二维数组 b[M][N] 中,若按行优先存储,则b[i][j] 的存储地址 = LOC + (i * N + j) * sizeof(ElemType);
- M行N列的二维数组 b[M][N] 中,若按列优先存储,则b[i][j] 的存储地址 = LOC + ( j * M+ i ) * sizeof(ElemType)
普通矩阵的存储
描述矩阵元素时,行、列号通常从 1 开始;而描述数组时通常下标从0开始(注意审题)
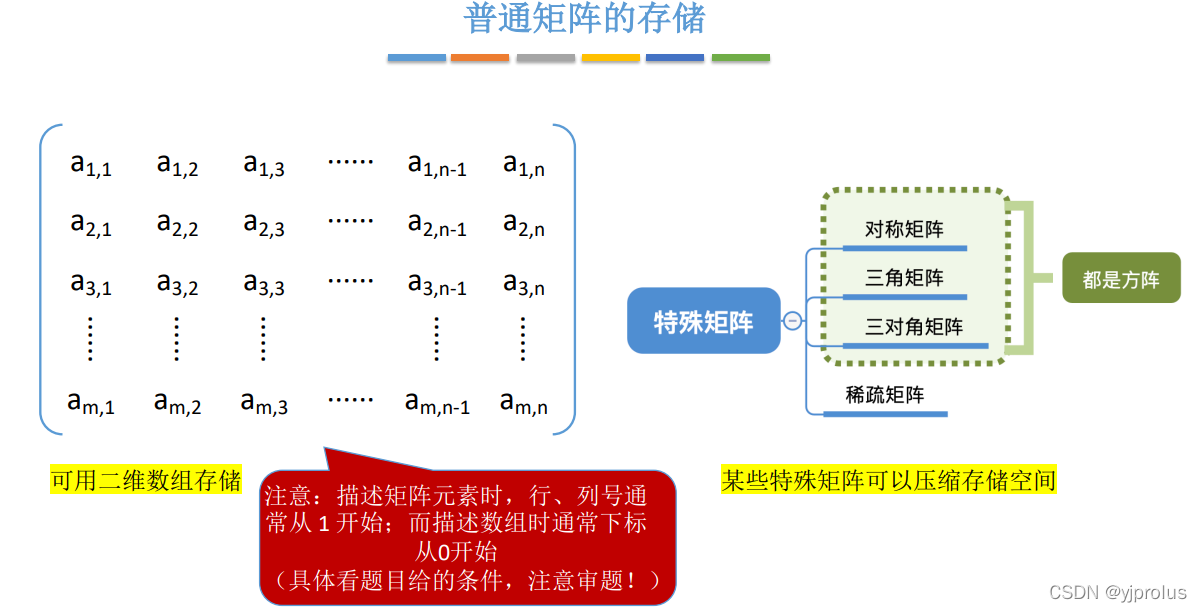
对称矩阵的压缩存储
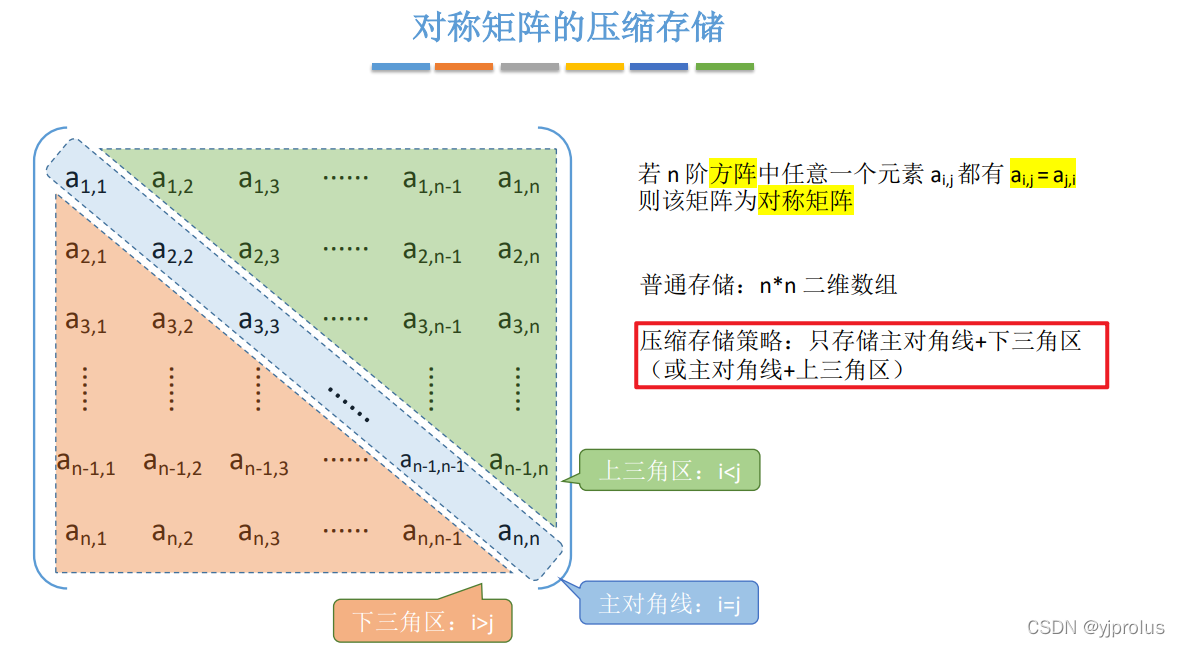
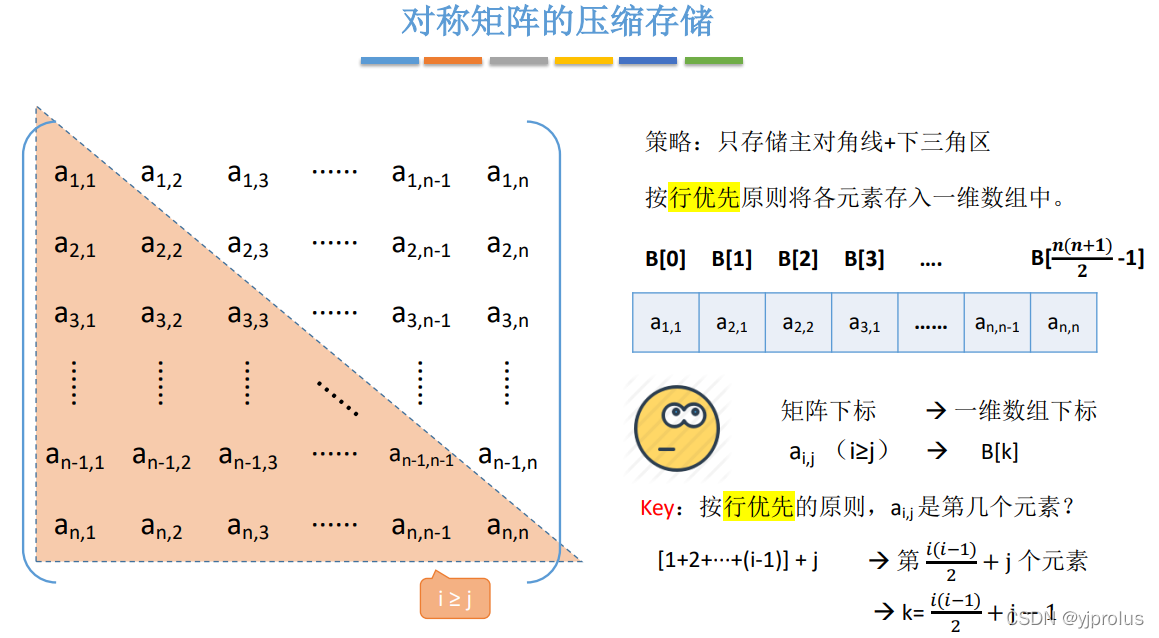
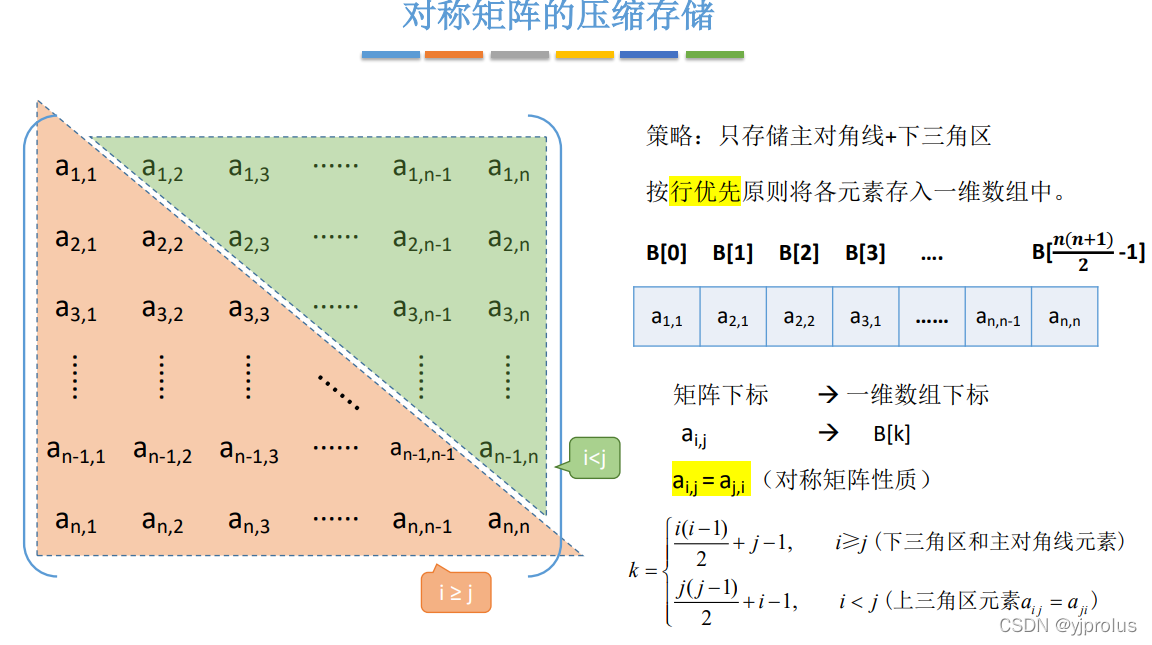
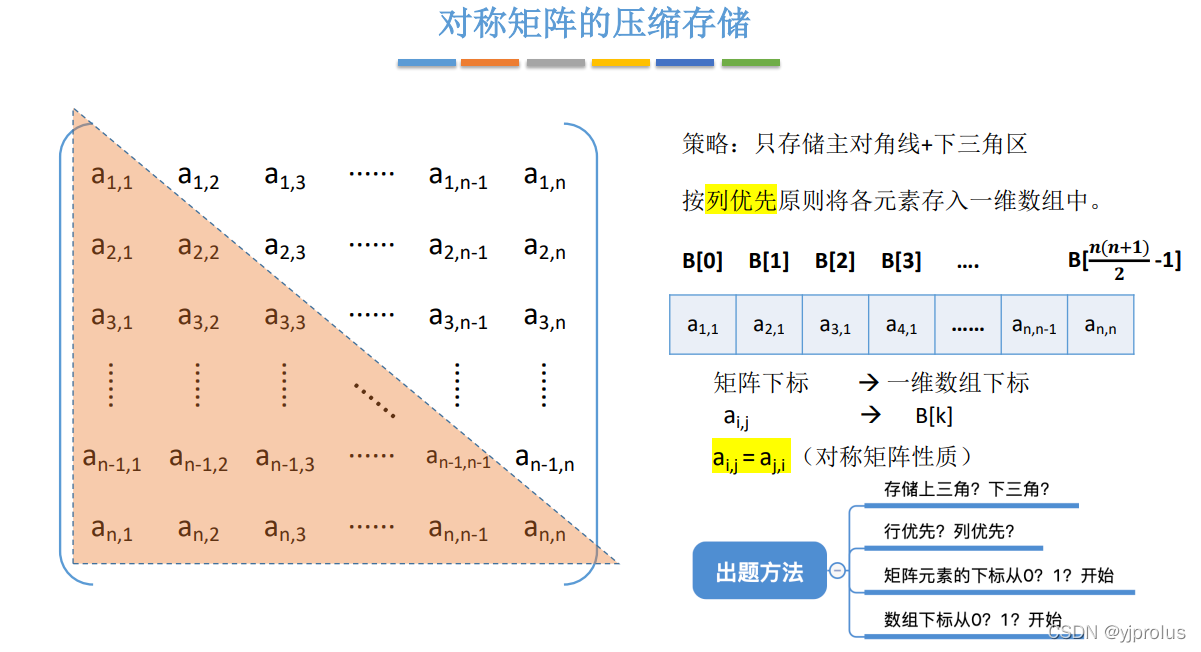
三角矩阵的压缩存储
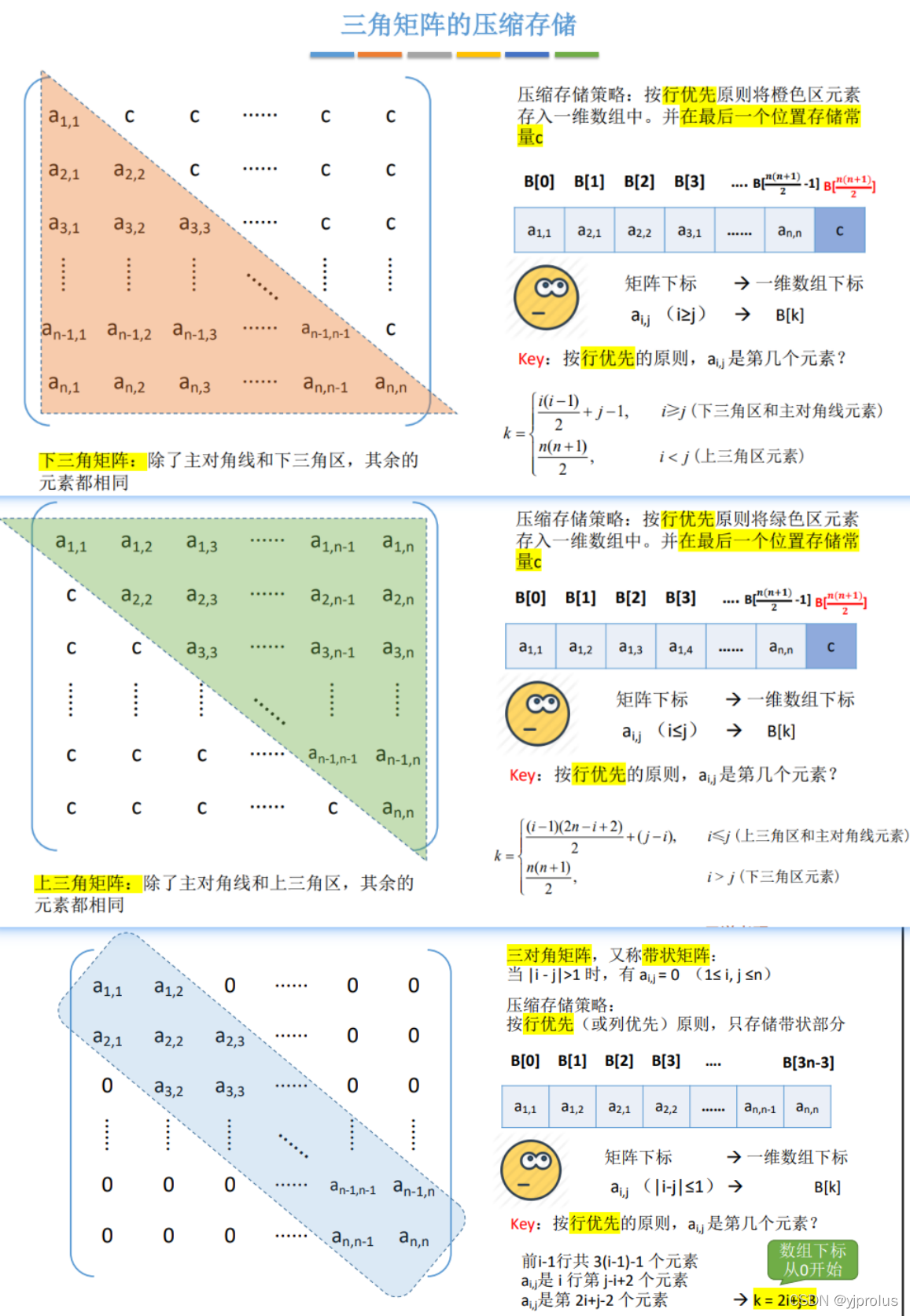

稀疏矩阵的压缩存储
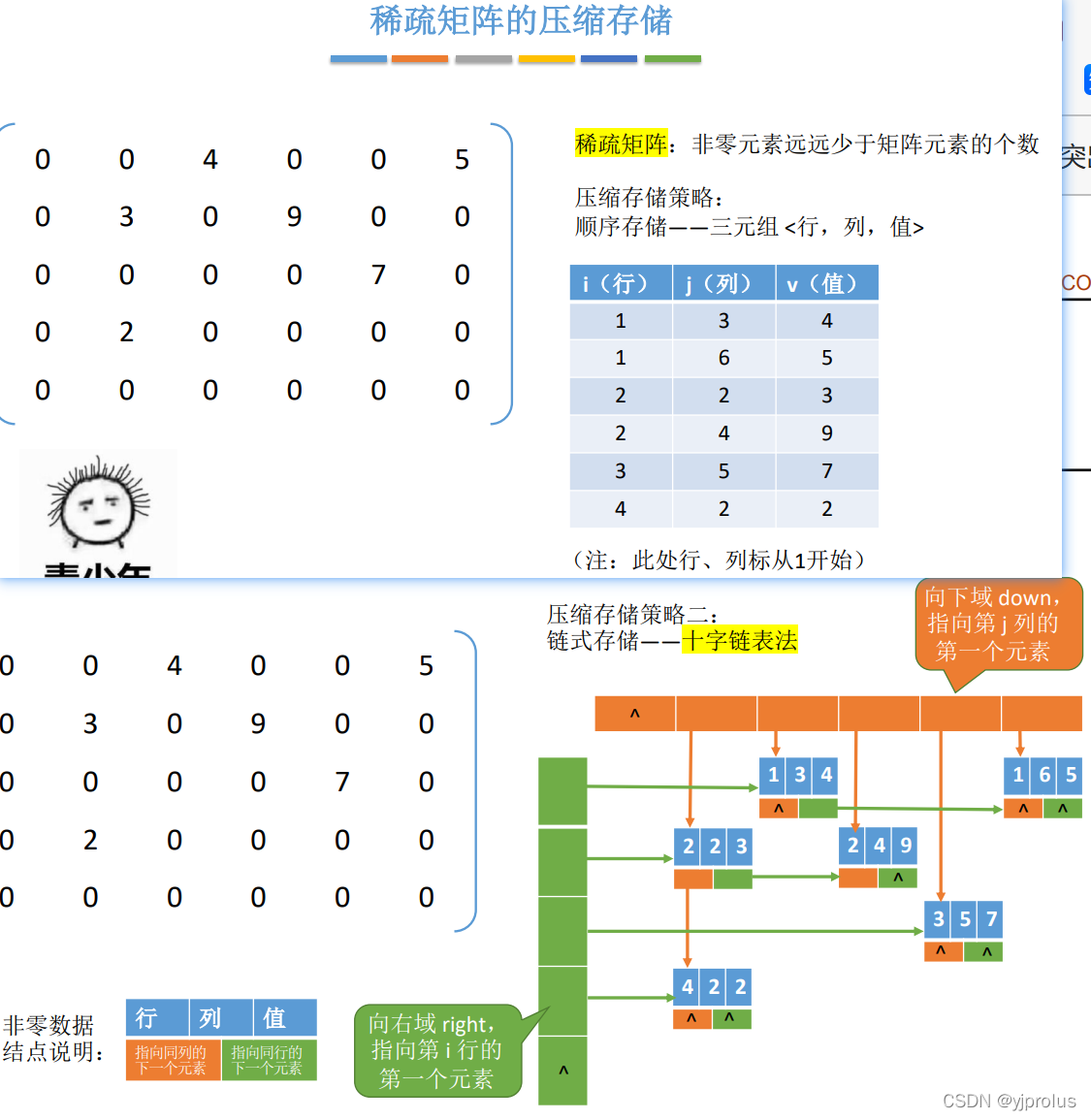
总结
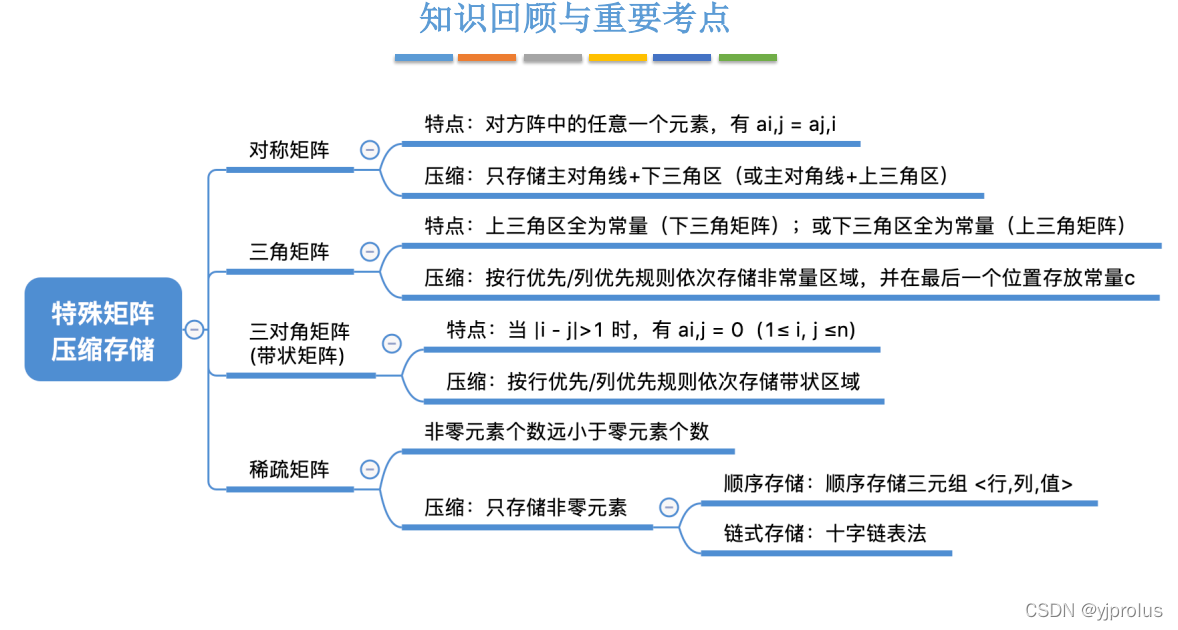
3.5队列的应用
树的层次遍历
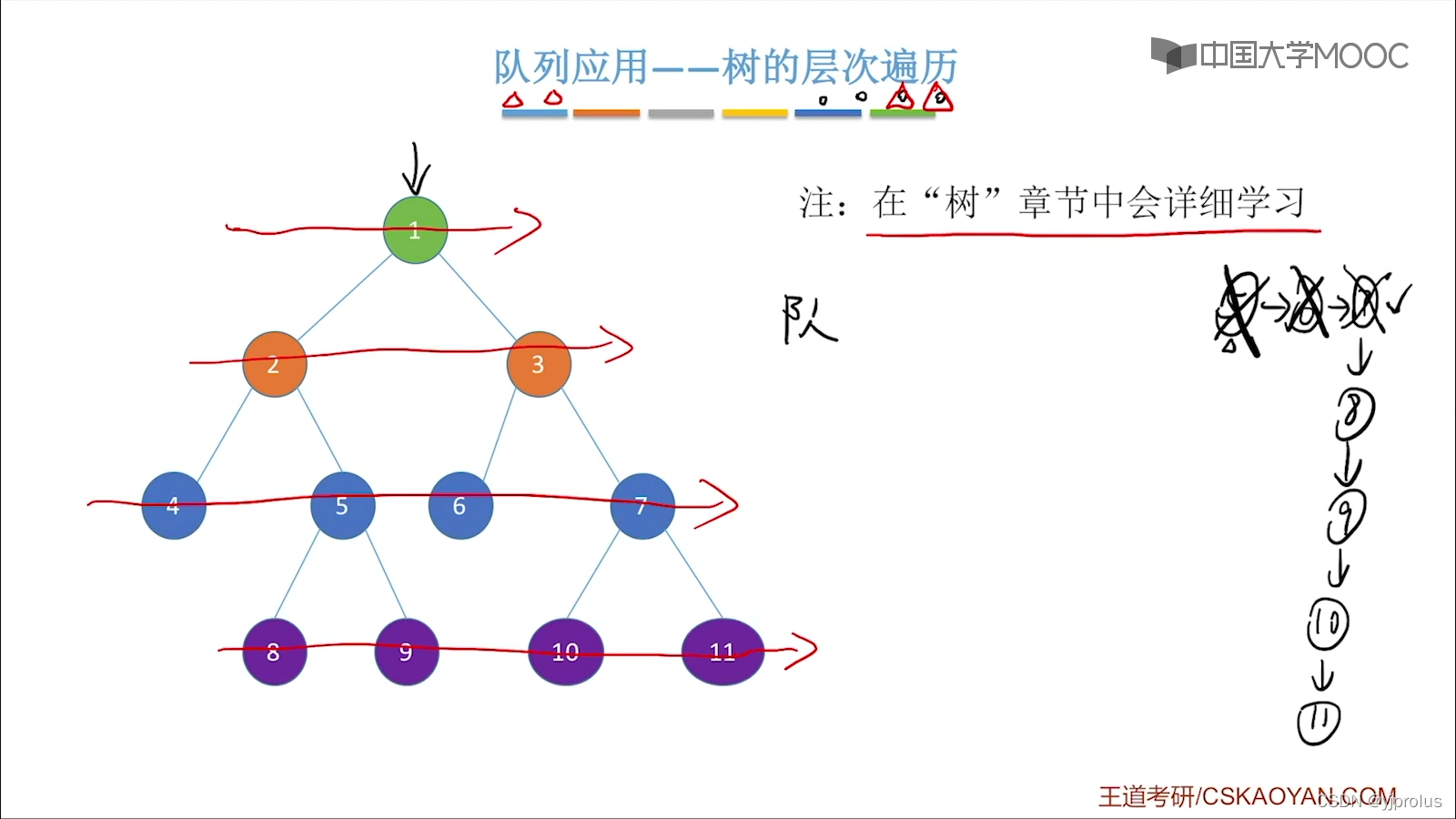
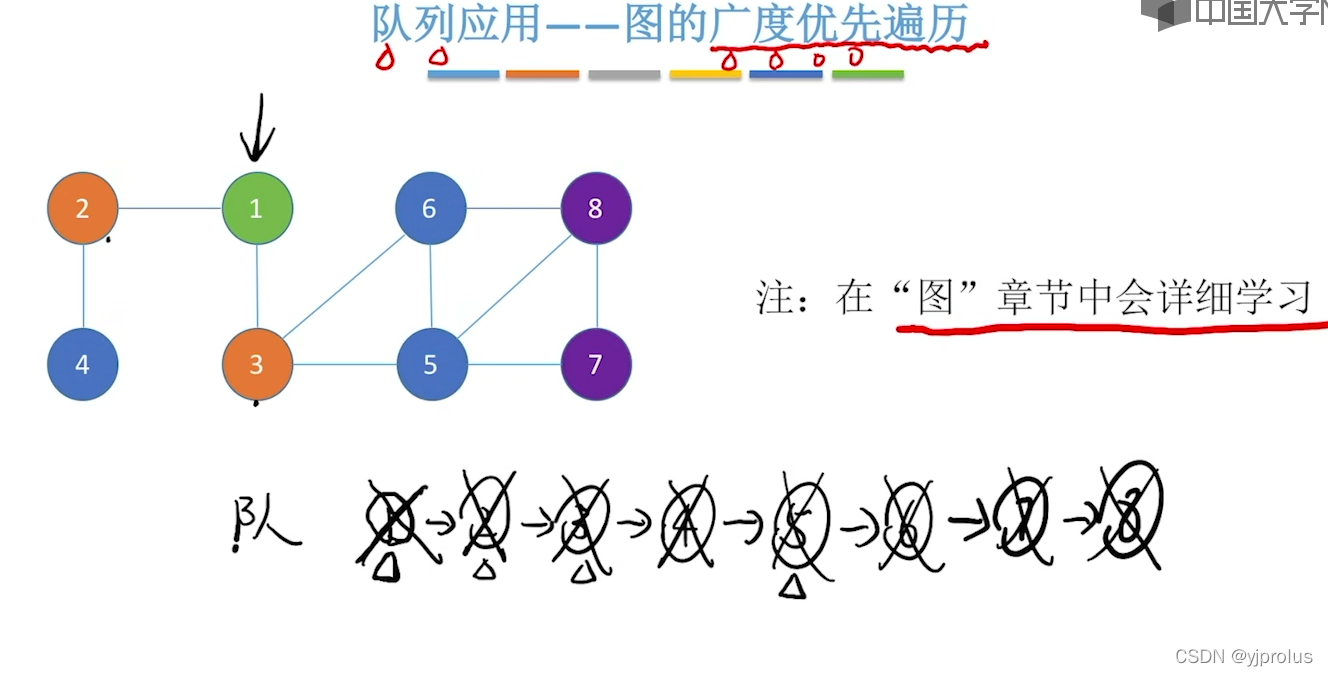
图的广度优先遍历
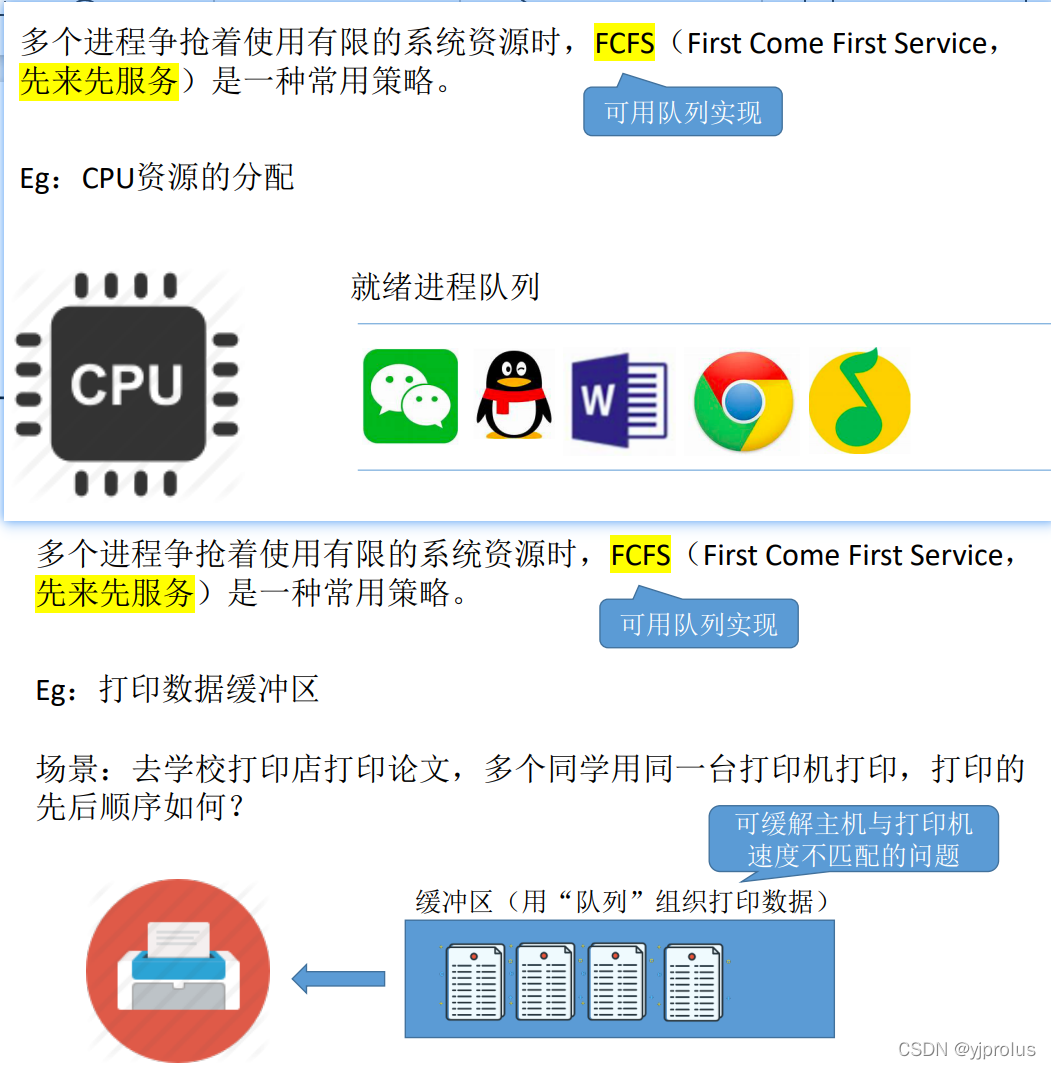
队列在操作系统中的应用