串: 串(string)是由零个或多个字符组成的有限序列,又名字符串。一般记为s=""(n≥0),零个字符的串称为空串(null string)。
????????空格串,是只包含空格的串。注意它与空串的区别,空格串是有内容由长度的,而且可以不止一个空格。
????????子串与主串,串中任意个数的连续字符组成的子序列称为该串的子串,相应地,包含子串的串称为主串。
子串在主串中的位置就是子串的第一个字符在主串中的序号
?????????????????????????????????????????串的抽象数据类型
ADT 串(string)
Data
串中元素仅由一个字符组成,相邻元素具有前驱和后驱关系
Operation
StrAssign(T,*chars):生成一个其值等于字符串常量chars的串T。
StrCopy(T,S):串S存在,由串S复制得串T
ClearString(S):串S存在,将串清空
StringEmpty(S):若串S为空,返回true,否则返回false
StrLength(S):返回串S的元素个数,即串的长度。
StrCompare(S,T):若S>T,返回值>0,若S=T,返回值0,若S<T,返回值<0。
Concat(T,S_1,S_2):用T返回由S_1和S_2联结而成的新串。
SubString(Sub,S,pos,len):串S存在,1≤pos≤StrLength(S),且0≤len≤StrLength(S)-pos+1,用Sub返回串S的第pos个字符起长度为len的子串。
Index(S,T,pos):串S和T存在,T是非空串,1≤pos≤StrLength(S)。若主串S中存在和串T值相同的子串,则返回它在主串S中第pos个字符之后第一次出现的位置,否则返回0。
Replace(S,T,V):串S、T和V存在,T是非空串。用V替换主串S中出现的所有与T相等的不重叠的子串。
StrInsert(S,pos,T):串S和T存在,1≤pos≤StrLength(S)+1。在串S的第pos个字符之前插入串T.
StrDelete(S,pos,len):串S存在,1≤pos≤StrLength(S)-len+1。从串S中删除第pos个字符起长度为len的子串。
endADT操作Index的实现算法:
/* T为非空串。若主串S中第pos个字符之后存在与T相等的子串, */
/* 则返回第一个这样的子串在S中的位置,否则返回0 */
int Index2(String S, String T, int pos)
{
int n,m,i;
String sub;
if (pos > 0)
{
n = StrLength(S); /* 得到主串S的长度 */
m = StrLength(T); /* 得到子串T的长度 */
i = pos;
while (i <= n-m+1)
{
SubString (sub, S, i, m); /* 取主串中第i个位置长度与T相等的子串给sub */
if (StrCompare(sub,T) != 0) /* 如果两串不相等 */
++i;
else /* 如果两串相等 */
return i; /* 则返回i值 */
}
}
return 0; /* 若无子串与T相等,返回0 */
}串的存储结构
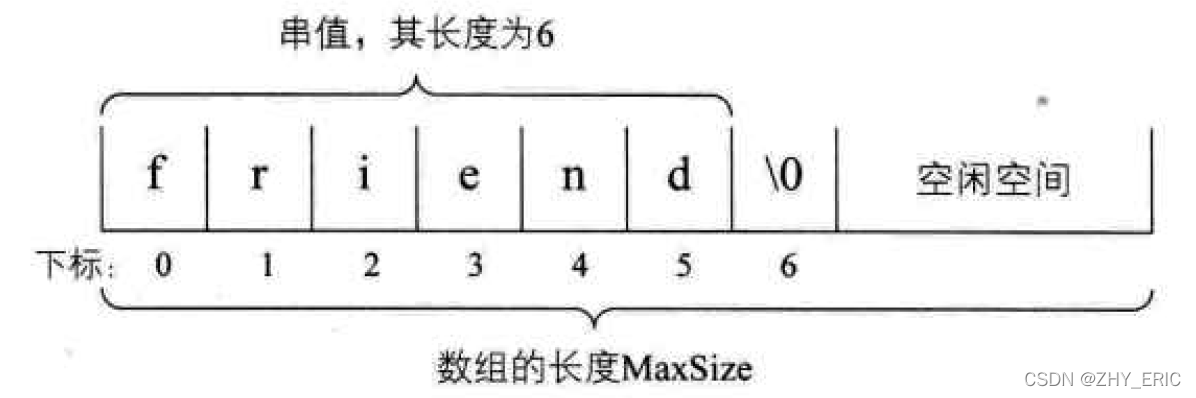
串的顺序存储结构:
????????串的顺序存储结构是用一组地址连续的存储单元来存储串中的字符序列的。按照预定义的大小,为每个定义的串变量分配一个固定长度的存储区。一般是用定长数组来定义。
串的链式存储结构:

朴素的模式匹配算法
/* 返回子串T在主串S中第pos个字符之后的位置。若不存在,则函数返回值为0。 */
/* 其中,T非空,1≤pos≤StrLength(S)。 */
int Index(String S, String T, int pos)
{
int i = pos; /* i用于主串S中当前位置下标值,若pos不为1,则从pos位置开始匹配 */
int j = 1; /* j用于子串T中当前位置下标值 */
while (i <= S[0] && j <= T[0]) /* 若i小于S的长度并且j小于T的长度时,循环继续 */
{
if (S[i] == T[j]) /* 两字母相等则继续 */
{
++i;
++j;
}
else /* 指针后退重新开始匹配 */
{
i = i-j+2; /* i退回到上次匹配首位的下一位 */
j = 1; /* j退回到子串T的首位 */
}
}
if (j > T[0])
return i-T[0];
else
return 0;
}KMP模式匹配算法?

?
?next数组值推导:


?

?KMP算法的实现:
/* 通过计算返回子串T的next数组。 */
void get_next(String T, int *next)
{
int i,k;
i=1;
k=0;
next[1]=0;
while (i<T[0]) /* 此处T[0]表示串T的长度 */
{
if(k==0 || T[i]== T[k]) /*T[i]表示后缀的单个字符,*/
/*T[K]表示前缀的单个字符,*/
{
++i;
++k;
next[i] = k;
}
else
k= next[k]; /* 若字符不相同,则k值回溯 */
}
}
这段代码的目的是计算当前要匹配的串T的next数组
/* 返回子串T在主串S中第pos个字符之后的位置。若不存在,则函数返回值为0。 */
/* T非空,1≤pos≤StrLength(S)。 */
int Index_KMP(String S, String T, int pos)
{
int i = pos; /* i用于主串S中当前位置下标值,若pos不为1,则从pos位置开始匹配 */
int j = 1; /* j用于子串T中当前位置下标值 */
int next[255]; /* 定义一next数组 */
get_next(T, next); /* 对串T作分析,得到next数组 */
while (i <= S[0] && j <= T[0]) /* 若i小于S的长度并且j小于T的长度时,循环继续 */
{
if (j==0 || S[i] == T[j]) /* 两字母相等则继续,与朴素算法增加了j=0判断 */
{
++i;
++j;
}
else /* 指针后退重新开始匹配 */
j = next[j];/* j退回合适的位置,i值不变 */
}
if (j > T[0])
return i-T[0];
else
return 0;
}????????这里需要强调,KMP算法仅当模式与主串之间存在许多“部分匹配”的情况下才体现出它的优势,否则两者差异不明显。
??KMP模式匹配算法的改进:
/* 求模式串T的next函数修正值并存入数组nextval */
void get_nextval(String T, int *nextval)
{
int i,k;
i=1;
k=0;
nextval[1]=0;
while (i<T[0]) /* 此处T[0]表示串T的长度 */
{
if(k==0 || T[i]== T[k]) /* T[i]表示后缀的单个字符,T[k]表示前缀的单个字符 */
{
++i;
++k;
if (T[i]!=T[k]) /* 若当前字符与前缀字符不同 */
nextval[i] = k; /* 则当前的j为nextval在i位置的值 */
else
nextval[i] = nextval[k]; /* 如果与前缀字符相同,则将前缀字符的 */
/* nextval值赋值给nextval在i位置的值 */
}
else
k= nextval[k]; /* 若字符不相同,则k值回溯 */
}
}? ? ? ? nextval数组值推导:
(暂时省略)