DFS算法思想–不撞南墙不回头

DFS经典问题
不带重复数字的全排列
输入n,再输入n个不重复数字,输出这n个数字的所有全排列组合。
#include<bits/stdc++.h>
using namespace std;
int n; //输入数字的个数
int num[1010]; //存放输入的数字
int a[1010]; //存放全排列
int b[1010]; //标记数组
void dfs(int t) {
//递归出口
if (t == n) {
for (int i = 0; i < n; i++) {
cout << a[i] << " ";
}
cout << endl;
return;
}
//递归条件
for (int i = 0; i < n; i++) {
if (!b[i]) {
a[t] = num[i];
b[i] = 1;
dfs(t + 1);
b[i] = 0;
}
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++) {
cin >> num[i];
}
sort(num, num + n); //为了全排列输出美观,这里我们将输入数字进行排序
dfs(0);
return 0;
}
带重复数字的全排列
输入n,再输入n个可能会重复的数字,输出这n个数字的所有全排列组合。
思路:dfs+剪枝,保证树的每一层只使用特定数字一次。
#include<bits/stdc++.h>
using namespace std;
int n; //输入数字的个数
int num[1010]; //存放输入的数字
int a[1010]; //存放全排列
int b[1010]; //标记数组
void dfs(int t) {
//递归出口
if (t == n) {
for (int i = 0; i < n; i++) {
cout << a[i] << " ";
}
cout << endl;
return;
}
//递归条件
for (int i = 0; i < n; i++) {
if (!b[i]) {
if (i > 0 && num[i] == num[i - 1] && b[i - 1] == 1) continue; //剪枝判断
a[t] = num[i];
b[i] = 1;
dfs(t + 1);
b[i] = 0;
}
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++) {
cin >> num[i];
}
sort(num, num + n); //为了全排列输出美观,这里我们将输入数字进行排序
dfs(0);
return 0;
}
走迷宫
输入n,m,表示迷宫有n行m列
输入起点startx,starty,终点endx,endy
输入n行m列的迷宫,1表示空地,2表示障碍物
输出从起点到终点的最短步数
#include<bits/stdc++.h>
using namespace std;
int n, m; //n行m列
int startx, starty, endx, endy; //起点,终点
int a[1010][1010]; //存放迷宫地图
int b[1010][1010]; //标记数组
int d[4][2] = {{-1, 0},{1, 0},{0, -1},{0, 1}}; //上下左右
int ans = 999999; //记录最少步数
void dfs(int x, int y, int t) { //t表示走过多少步
//递归出口
if (x == endx && y == endy) {
ans = min(ans, t);
return;
}
//递归条件
for (int i = 0; i <= 3; i++) {
int nextx = x + d[i][0];
int nexty = y + d[i][1];
if (!b[nextx][nexty] && a[nextx][nexty] == 1) {
b[nextx][nexty] = 1;
dfs(nextx, nexty, t + 1);
b[nextx][nexty] = 0;
}
}
}
int main()
{
cin >> n >> m;
cin >> startx >> starty >> endx >> endy;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j]; //1代表空地,2代表障碍物
}
}
b[startx][starty] = 1; //起点肯定已经被走过了
dfs(startx, starty, 0);
cout << ans << endl;
return 0;
}
队列做法???/???
方格取数
dfs做法
#include<bits/stdc++.h>
using namespace std;
int n, m;
int a[1010][1010]; //存放输入数字
int b[1010][1010]; //标记数组
int d[3][2] = {{-1, 0},{1, 0},{0, 1}}; //上下右
long long ans = -0xfffffff; //最大和
void dfs(int x, int y, long long t) { //t表示从起点走到(x,y)为止所算出的和
//递归出口
if (x < 1 || y < 1 || x > n || y > m) { //跑到地图外面了
return;
}
if (x == n && y == m) { //到终点了
ans = max(ans, t);
return;
}
//递归条件
for (int i = 0; i < 3; i++) {
int nextx = x + d[i][0];
int nexty = y + d[i][1];
if (!b[nextx][nexty]) {
b[nextx][nexty] = 1;
dfs(nextx, nexty, t + a[nextx][nexty]);
b[nextx][nexty] = 0;
}
}
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
}
}
b[1][1] = 1; //左上角肯定走过了
dfs(1, 1, a[1][1]);
cout << ans << endl;
return 0;
}
dfs做法是不能AC这道题的,只能拿25分,因为dfs复杂度太高,要想AC这道题应该用dp去做。
dp做法
待更…
素数环问题
从1到20这20个数摆成一个环,要求相邻的两个数的和是一个素数。
输出所有的这种素数环。
#include<bits/stdc++.h>
using namespace std;
int a[25]; //存放素数环
int b[25]; //记录数组
bool isPrime(int num) {
if (num == 1) return false;
if (num == 2) return true;
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
}
void dfs(int t) { //t表示已经填了t个数字了
//递归出口
if (t == 20) { //到目前为止已经选了20个数字了
if (isPrime(a[1] + a[20])) {
for (int i = 0; i < 20; i++) cout << a[i] << " ";
cout << endl;
}
return;
}
//递归条件
for (int i = 1; i <= 20; i++) {
if (!b[i] && isPrime(i + a[t - 1])) {
a[t] = i;
b[i] = 1;
dfs(t + 1);
b[i] = 0;
}
}
}
int main()
{
dfs(0);
return 0;
}
数独
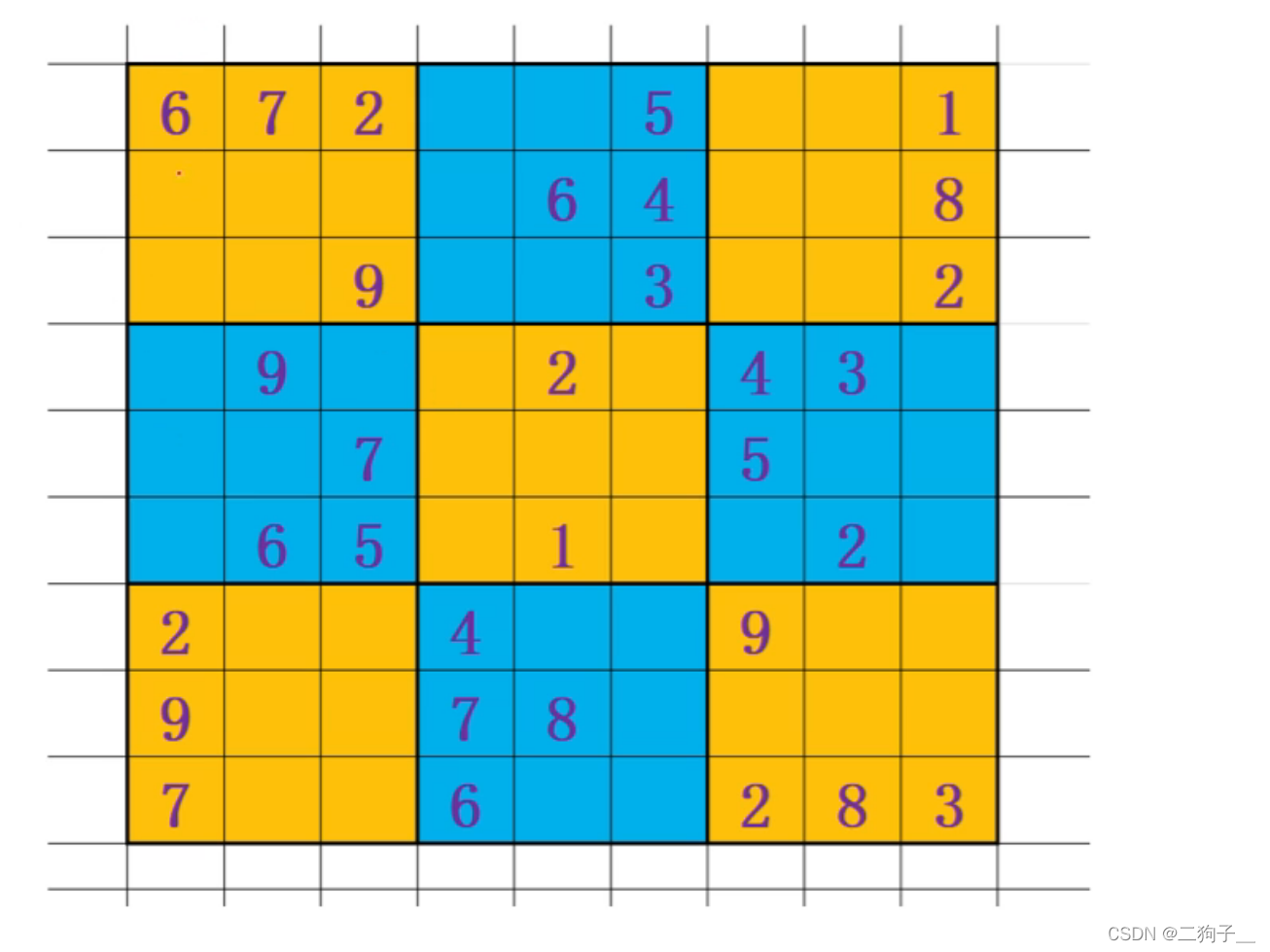
同一行不能有重复数字、同一列不能有重复数字、3×3格子内不能有重复数字。
请把已给的未填满的九宫格填满。
#include<bits/stdc++.h>
using namespace std;
int a[15][15]; //九宫格
bool check(int x, int y, int num) {
//检查同一行、同一列
for (int i = 1; i <= 9; i++) {
if (a[x][i] == num) return false;
if (a[i][y] == num) return false;
}
//检查小九宫格
for (int i = (x - 1) / 3 * 3 + 1; i <= ((x - 1) / 3 + 1) * 3; i++) {
for (int j = (y - 1) / 3 * 3 + 1; j <= ((y - 1) / 3 + 1) * 3; j++) {
//这里i和j的范围比较麻烦,要稍微算一下
if (a[i][j] == num) return false;
}
}
return true;
}
void dfs(int x, int y) {
//递归出口
if (x == 10) {
cout << endl;
for (int i = 1; i <= 9; i++) {
for (int j = 1; j <= 9; j++) {
cout << a[i][j] << " ";
}
cout << endl;
}
return;
}
//递归条件
if (a[x][y] == 0) { //如果是空地
//cout << "???" << endl;
//那就考虑填哪个数字
for (int i = 1; i <= 9; i++) {
if (check(x, y, i)) {
a[x][y] = i;
dfs(x + y / 9, y % 9 + 1); //按照从上到下、从左到右的顺序遍历九宫格
a[x][y] = 0;
}
}
}
else { //如果不是空地
dfs(x + y / 9, y % 9 + 1);
}
}
int main()
{
//构造初始九宫格
for (int i = 1; i <= 9; i++) {
for (int j = 1; j <= 9; j++) {
cin >> a[i][j];
}
}
//填充九宫格
dfs(1, 1);
return 0;
}
样例输入输出:
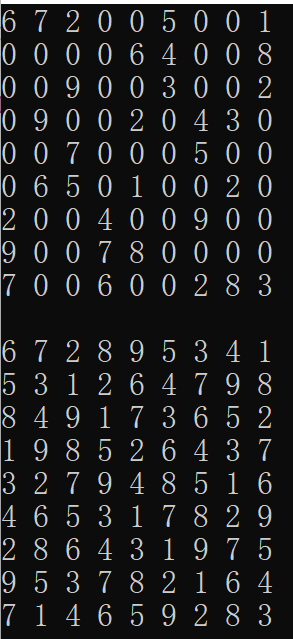
n皇后
输入n,然后你现在有一个n×n的方格,n个皇后要放在这些方格中,且她们两两不在一行、不在一列、不在一条对角线上。
输出有多少种放法。
#include<bits/stdc++.h>
using namespace std;
int n;
int ans;
int a[100]; //第i行的皇后在第a[i]列
bool check(int t, int col) { //判断第t行、第col列能不能放皇后
for (int i = 1; i <= t; i++) { //遍历前t行
if (a[i] == col) return false; //检查同列
if (t - col == i - a[i]) return false; //检查正对角线
if (t + col == i + a[i]) return false; //检查负对角线
}
return true;
}
void dfs(int t) { //t表示前 t - 1 行的皇后位置已经确定了,即将确定第 t 行的皇后位置
//递归出口
if (t == n + 1) {
ans++;
return;
}
//递归条件
for (int col = 1; col <= n; col++) {
if (check(t, col)) {//如果第t行、第col列可以放皇后
a[t] = col;
dfs(t + 1);
a[t] = 0;
}
}
}
int main()
{
cin >> n;
dfs(1);
cout << ans << endl;
return 0;
}
dfs模板

总结
