文章目录
40. 组合总和 II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]
提示:
1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30
分析
- 这道题目是之前组合问题的提升版本。主要难点是不能让有重复元素的集合的解集重复。
- 如果直接使用set去重势必会耗费大量的时间,所以这里必须在遍历的时候去重,关键点就是在什么地方去重呢?
我们允许递归的时候有着相同元素的存在,但却不允许相同元素在同一层出现。所以这里我们应该在for循环里面使用以i>start作为判定条件之一,保证至少同一层有两个元素,且上一个元素不能等于下一个元素,如果等于了,直接跳过(continue)。 - 剪枝操作:和大于target即return
代码
res = []
path = []
nums.sort()
def backtrack(start):
res.append(path[:])
if len(path) >= len(nums):
return
for i in range(start,len(nums)):
if i > start and nums[i] == nums[i-1]:
continue
path.append(nums[i])
backtrack(i+1)
path.pop()
backtrack(0)
return res
通过截图
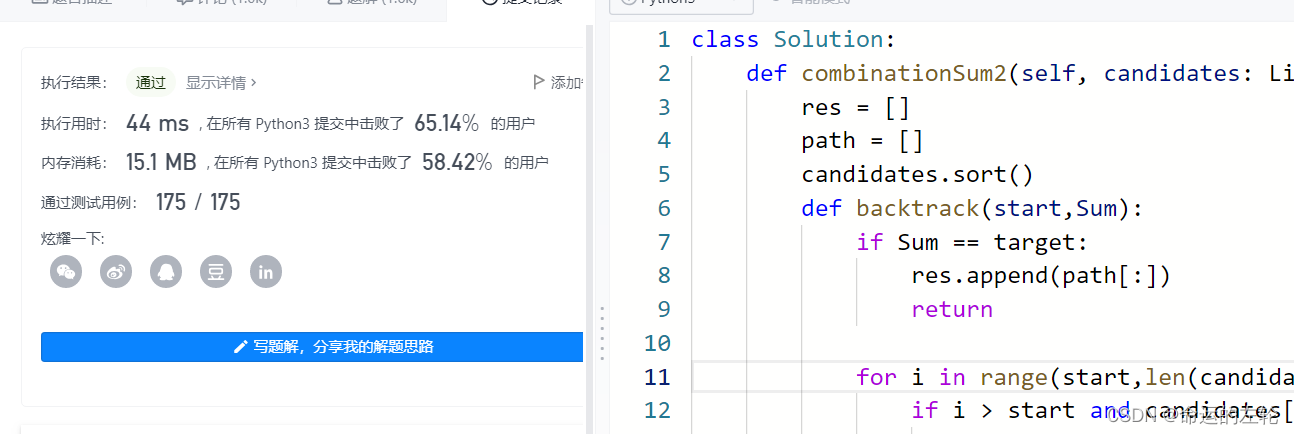
小总结
有关组合的题目
包括本篇LeetCode70,
LeetCode77,216
LeetCode17,39
- 有关组合的题目大概到这里就结束了,我们会发现在这类问题中,回溯算法是非常好用的。现在总结一下关于此类问题的一些经验:
- 在单集合问题中,可以用一个start来表示搜索位置,具体搜索的范围一般不剪枝的话,就是(start,len(单集合))
- 多集合的问题中,要取出每一个集合,然后遍历每一个集合。
- 剪枝时视情况而定,比如求和的剪枝可以先排序,超过目标值再剪枝,超过集合长度剪枝等等。
for i in range(start,...)
- 递归时,如果允许重复就:递归到i 不允许重复就到下一个元素,递归到i+1
- 不要递归到start和start+1,两者是不一样的(我也不知道该怎么解释)
- 做此类问题可以画一棵树图帮助理解和写代码。 横向遍历是for循环,纵向遍历是递归。
如有错误,敬请指正,欢迎交流,谢谢?(・ω・)ノ