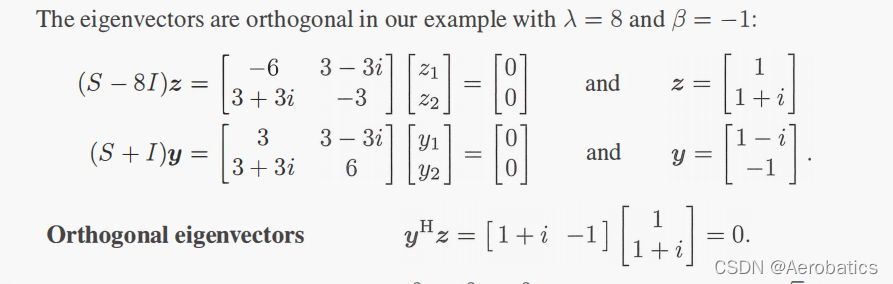1.厄米特矩阵(Hermittan Matrix)
1.1 共轭转置
向量的共轭转置

矩阵的共轭转置

1.2 复向量的长度
实向量的长度
x
T
x
=
[
x
1
?
x
n
]
[
x
1
?
x
n
]
=
∣
x
1
∣
2
+
?
+
∣
x
n
∣
2
\boldsymbol{x}^T\boldsymbol{x}= \begin{bmatrix}x_1\cdots x_n\end{bmatrix} \begin{bmatrix}x_1 \\ \vdots\\x_n\end{bmatrix}= |x_1|^2+\cdots+|x_n|^2
xTx=[x1??xn??]????x1??xn??????=∣x1?∣2+?+∣xn?∣2
复向量的长度
我们假设其长度为
z
T
z
=
[
z
1
?
z
n
]
[
z
1
?
z
n
]
=
∣
z
1
∣
2
+
?
+
∣
z
n
∣
2
=
0
z^Tz=\begin{bmatrix}z_1\cdots z_n\end{bmatrix}\begin{bmatrix}z_1\\ \vdots\\ z_n\end{bmatrix}=|z_1|^2+\cdots+|z_n|^2=0
zTz=[z1??zn??]????z1??zn??????=∣z1?∣2+?+∣zn?∣2=0
假设
z
1
=
1
+
i
z_1=1+i
z1?=1+i 则
∣
z
1
∣
2
=
(
1
+
i
)
(
1
+
i
)
=
1
+
i
2
=
0
|z_1|^2=(1+i)(1+i)=1+i^2=0
∣z1?∣2=(1+i)(1+i)=1+i2=0,一个非零向量其长度为0显然不符合事实,这是因为虚数
i
i
i的原因,所以复向量的长度为
z
ˉ
T
z
=
z
H
z
\bar{z}^Tz=z^Hz
zˉTz=zHz【
H
H
H代表共轭转置】

1.3 复向量内积


1.4 厄米特矩阵
对于实对称矩阵 S = S T S=S^T S=ST,有实特征值、正交矩阵 Q Q Q中有特征向量、可以分解为 S = Q Λ Q ? 1 S=Q\Lambda Q^{-1} S=QΛQ?1 因为 Q ? 1 = Q Q^{-1}=Q Q?1=Q 所以 S = Q Λ Q T S=Q\Lambda Q^T S=QΛQT
在复数矩阵中,有一类特殊矩阵,即 A = A H A=A^H A=AH【其中 H H H 代表共轭转置 A H = A ˉ T A^H=\bar{A}^T AH=AˉT】

如果矩阵
A
A
A是对称矩阵
S
S
S,则
S
=
S
H
S=S^H
S=SH

对称厄米特矩阵:主对角线上都是实数、副对角线上为复数共轭 s i j = s ˉ i j s_{ij}=\bar{s}_{ij} sij?=sˉij?
对称厄米特矩阵的三个性质
性质一:


性质二:


性质三:

S
z
=
λ
z
?
y
H
S
z
=
y
H
λ
z
S\boldsymbol{z}=\lambda\boldsymbol{z}\\ ~\\ \boldsymbol{y}^HS\boldsymbol{z}=\boldsymbol{y}^H\lambda\boldsymbol{z}
Sz=λz?yHSz=yHλz
S y = β y ? y H S H = β y H ? y H S H z = β y H z S\boldsymbol{y}=\beta\boldsymbol{y}\\ ~\\ \boldsymbol{y}^HS^H=\beta\boldsymbol{y}^H\\ ~\\ \boldsymbol{y}^HS^H\boldsymbol{z}=\beta\boldsymbol{y}^H\boldsymbol{z}\\ Sy=βy?yHSH=βyH?yHSHz=βyHz
y
H
S
z
=
y
H
λ
z
?
y
H
S
H
z
=
β
y
H
z
\boldsymbol{y}^HS\boldsymbol{z}=\boldsymbol{y}^H\lambda\boldsymbol{z}\\ ~\\ \boldsymbol{y}^HS^H\boldsymbol{z}=\beta\boldsymbol{y}^H\boldsymbol{z}
yHSz=yHλz?yHSHz=βyHz
因为
S
=
S
H
S=S^H
S=SH,所以
y
H
λ
z
=
β
y
H
z
\boldsymbol{y}^H\lambda\boldsymbol{z}=\beta\boldsymbol{y}^H\boldsymbol{z}
yHλz=βyHz,又因为
λ
≠
β
\lambda\neq\beta
λ?=β,所以
y
H
z
=
0
\boldsymbol{y}^H\boldsymbol{z}=0
yHz=0,故特征向量
y
、
z
\boldsymbol{y}、\boldsymbol{z}
y、z 互相垂直