[数据结构与算法]leetcode记录-167-两数之和-双指针

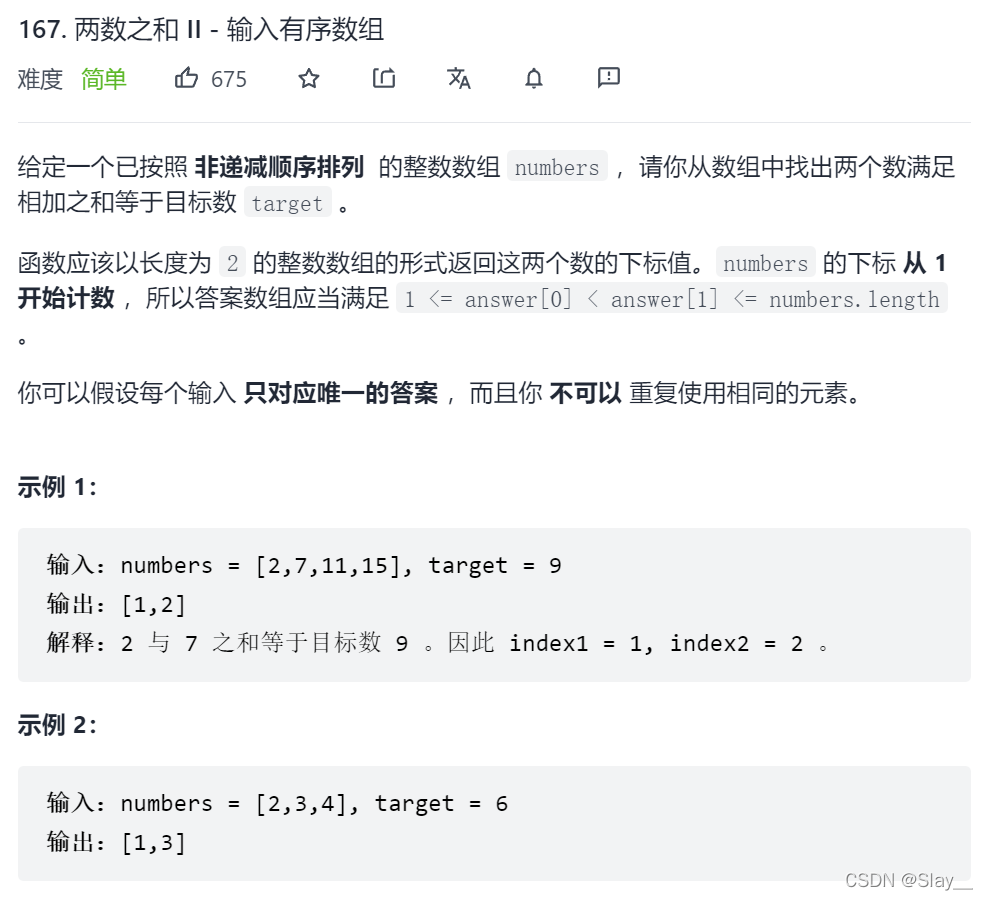
167.两数之和

思路

1. 如果本题没说递增数列，解法就是普通的O(n^2)的遍历。
2. 但是本题说了！！！递增数列，所以就要充分利用递增数列的特性，两数求和等于target，从首尾开始，不同情况移动不同的下标，直到找到，因为第一个数加最后一个数和最后一个数加第一个数没区别，所以中间汇聚即可，肯定能找到。

代码

1. 如果不是递增数列的解法：
   ①while循环：

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int index1=0;
        int index2=1;
        int[] end=new int[2];
        while(index1<numbers.length-1){
            if (index2==numbers.length){ //搜索元素到头了，标准元素+1
                index1++;
                index2=index1+1;
            } else if (numbers[index2]+numbers[index1]==target){ //找到了
                end[0]=index1+1;
                end[1]=index2+1;
                break;
            } else { //搜索元素步进
                index2++;
            }
        }
        return end;
    }
}

②for循环：

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int index1=0;
        int index2=1;
        int[] end=new int[2];
        for (int i = 0; i < numbers.length-1; i++) {
            for (int j = i+1; j < numbers.length; j++) {
                if (numbers[i]+numbers[j]==target){
                    end[0]=i+1;
                    end[1]=j+1;
                }
            }
        }
        return end;
    }
}

2. 递增序列的双指针：

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int index1=0;
        int index2=numbers.length-1;
        while (index1<index2){
            if (numbers[index1]+numbers[index2]<target)
                index1++;
            else if (numbers[index1]+numbers[index2]>target)
                index2--;
            else {
                return new int[]{index1+1,index2+1};
            }
        }
        return new int[]{index1+1,index2+1};
    }
}

技巧和总结

1. 分析搜索空间，看暴力解法能否优化，一般元素按序的如果需要O(n^2)的考虑双指针。
2. 遍历的方法多样，多思考。