算法之排序篇介绍
文章目录
一、认识时间复杂度?
时间复杂度为,一个算法流程中,常数操作数量的指标,这个指标叫做O,bigO,如果常数操作数量的表达式中,只要高阶项,不要低阶项,也不要高阶项系数之后,剩下的部分记为f(N),那么该算法的时间复杂度为O(f(N))
题目一:在一个数组中找到数组的最大值
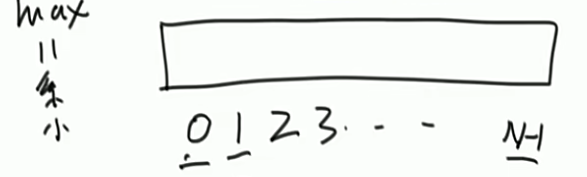
在这个遍历的过程中,每次都取出数组中一个位置的数字和max比较,这个过程,取出数组的i位置的数据是1个常数操作,比较是另一个常数操作,所以每个位置的是两个常数操作,这个过程一共有N次,那么就是O(N)*2那么时间复杂度就是O(N)。
package exercise;
public class GetMaxElement {
/***
* 获取数组的最大值
* @param arr
* @return
*/
public int getMaxElement(int[]arr)
{
if(arr==null) return Integer.MIN_VALUE;
int max=Integer.MIN_VALUE;
for (int i = 0; i <arr.length ; i++) {
//取值和比较是常数级操作
if(arr[i]>max) max=arr[i];
}
return max;
}
}
题目二:选择排序(时间:O(N^2) 空间:O(1))
步骤:每次从后面的N个数中,选择最小的数字,放到前面
时间复杂度:每次从后面的N个数字中选出最小数的时间复杂度是O(N),这样总的时间复杂度是O(N)+O(N-1)+O(N-2)+…O(1):这样求和是O(N^2)舍弃N的低次方和二次方前面的系数。
package ArrraySort;
public class SelectSort {
public void selectSort(int[]arr){
if(arr==null||arr.length<2) return;
// N-1次将后面数组的最小值放到数组前面
for (int i = 0; i <arr.length-1 ; i++) {
//记录数组i-N-1中的最小值下标
int index=i;
for (int j = i+1; j <arr.length ; j++) {
if(arr[j]<arr[index]){
index=j;
}
}
swap(arr,i,index);
}
}
/**
* 将数组i j位置进行交换
* @param arr
* @param i
* @param j
*/
public void swap(int[] arr,int i,int j)
{
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}
题目三:在一个已经排好序的数组中,找到目标值aim
步骤:用二分法查找,时间复杂度O(logN)
代码:
package exercise;
public class FindAimElement {
/***
* 从已经排好序的数组中找到目标数
* @param arr
* @return
*/
public int findAimElement(int[] arr,int aim,int L,int R){
if(L==R){
if(arr[L]==aim) return L;
return -1;
}
//如果中间这个是目标,那么返回目标下标
int mid=L+(R-L)/2;
if(arr[mid]==aim) return mid;
//循环递归寻找左边和右边的目标
int left=findAimElement(arr,aim,L,mid);
int right=findAimElement(arr,aim,mid+1,R);
//进行左右结果判断
return left!=-1?left:right!=-1?right:-1;
}
}
题目四:找到两个已经排好序的数组中的公有数字
方法一:暴力破解,在arr1数组中的每个数字都在arr2中进行遍历查找,时间复杂度是O(N*M)
代码:(优化:可以判断数字是否比后面的小,如果小,那么没有继续往后面比较的必要)
public ArrayDeque<Integer> findSameWord1(int[] arr1, int[] arr2){
if(arr1==null||arr2==null||arr1.length<1||arr2.length<1) return null;
ArrayDeque<Integer> result=new ArrayDeque<>();
for (int i = 0; i < arr1.length; i++) {
for (int j = 0; j <arr2.length ; j++) {
if(arr1[i]==arr2[j]){
result.add(arr1[i]);
break;
}
if(arr1[i]<arr2[j]) break;
}
}
return result;
}
方法二:在arr1数组中的每个数字在arr2中进行二分查找,时间复杂度O(N*logM)
/***
* 找到两个已经排好序的数组中的公有数字
* @param arr1 :已经排好序的数组1
* @param arr2 :已经排好序的数组2
*/
public ArrayDeque<Integer> findSameWord2(int[] arr1, int[] arr2){
if(arr1==null||arr2==null||arr1.length<1||arr2.length<1) return null;
ArrayDeque<Integer> result=new ArrayDeque<>();
FindAimElement findAimElement=new FindAimElement();
for (int i = 0; i < arr1.length; i++) {
//二分查找arr2数组中是否存在arr1数组元素
if(findAimElement.findAimElement(arr2,arr1[i],0,arr2.length-1)!=-1)
{
result.add(arr1[i]);
};
}
return result;
}
方法三:arr1数组和arr2数组两边交替查找数字,时间复杂度:O(N+M)

/***
* 找到两个已经排好序的数组中的公有数字
* @param arr1 :已经排好序的数组1
* @param arr2 :已经排好序的数组2
*/
public ArrayDeque<Integer> findSameWord3(int[] arr1, int[] arr2){
if(arr1==null||arr2==null||arr1.length<1||arr2.length<1) return null;
ArrayDeque<Integer> result=new ArrayDeque<>();
int p=0;//p是arr1目前遍历的位置
int q=0;//q是arr2目前遍历的位置
while(p<arr1.length&&q<arr2.length){
if(arr1[p]==arr2[q]){
result.add(arr1[p]);
++p;
++q;
continue;
}else{
if(arr1[p]<arr2[q])
{
p=p+1;
} else{
q=q+1;
}
}
}
return result;
}
| 方法 | 时间复杂度 |
|---|---|
| 方法一 | O(N*M) |
| 方法二 | O(N*logM) |
| 方法三 | O(N+M) |
方法二和三在不同的时候,都有可能会变得优秀
二、认识空间复杂度?
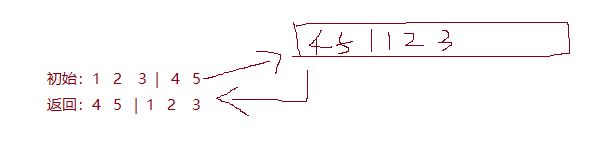
题目一:实现数组的下列变换

方法一:开辟额外数组空间,将后面的数据先放入数组,然后再放入前面的数,最后将额外数组空间的值拷贝回原数组空间:空间复杂度:O(N)
代码:
package exercise;
public class Array_leftAndright_Reverse {
/***
* 实现数组arr再m的左右翻转
* 时间复杂度:O(N)
* 空间复杂度:O(N)
* @param arr
* @param m
*/
public void messure1(int[] arr,int m){
if(arr==null||arr.length<1||m>arr.length-1||m<0) return ;
int[] arr1=new int[arr.length];
int index=0;
int p=m;
//进行原数组右边先拷贝到左边
while (p<arr.length){
arr1[index++]=arr[p++];
}
p=0;
//将原数组左边拷贝到右边
while (p<m){
arr1[index++]=arr[p++];
}
//最后进行整体的拷贝
for (int i = 0; i <arr.length ; i++) {
arr[i]=arr1[i];
}
}
}
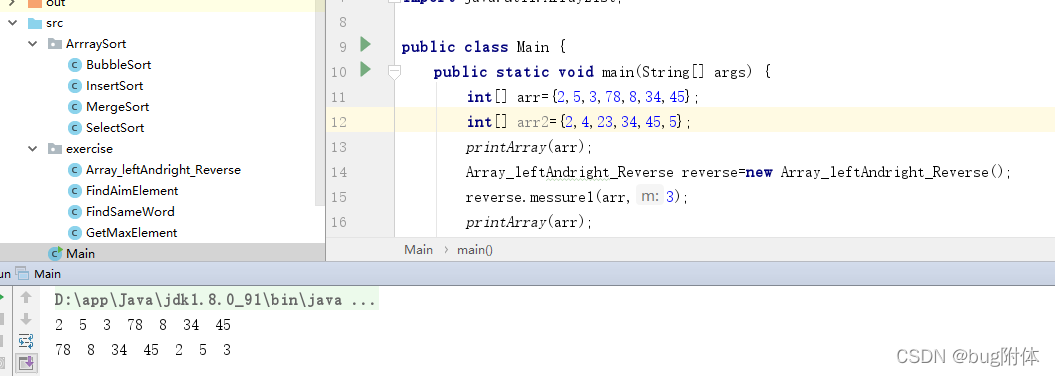
方法二:先左右进行逆序,再整体逆序
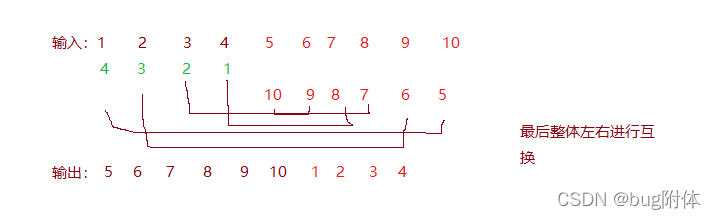
/***
* 方法二:先左右进行逆序,再整体逆序
* @param arr
* @param m
*/
public void messure2(int[] arr,int m){
if(arr==null||arr.length<1||m>arr.length-1||m<0) return ;
//先进行左边逆序
reverse(arr,0,m-1);
//再进行右边逆序
reverse(arr,m,arr.length-1);
//再进行整体逆序
reverse(arr,0,arr.length-1);
}
/***
* 从L到R位置逆序,包括L和R
* @param arr
* @param L
* @param R
*/
public void reverse(int[] arr,int L,int R){
while(L<R){
swap(arr,L++,R--);
}
}
/**
* 将数组i j位置进行交换
* @param arr
* @param i
* @param j
*/
public void swap(int[] arr,int i,int j)
{
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
三、经典排序算法的实现?
1、冒泡排序(稳定)
| 性能 | 指标 |
|---|---|
| 时间复杂度 | O(n^2) |
| 空间复杂度 | O(1) |
| 稳定性 | 稳定 |
代码实现:
package ArrraySort;
/**
* 冒泡排序:
* 时间复杂度:O(n^2)
* 空间复杂度:O(1)
* 稳定性:稳定
*/
public class BubbleSort {
/**
* 对整形数组进行排序
* @param array
*/
public void bubbleSort(int[] array){
if(array==null||array.length==0||array.length==1) return;
// 冒泡循环的次数n-1次
for (int i = array.length-1; i >0 ; i--) {
// 冒泡一次将最大的放到最后
for (int j = 0; j <i ; j++) {
if(array[j]>array[j+1]){
swap(array,j,j+1);
}
}
}
}
/**
* 冒泡排序加强版本
* @param array
*/
public void bubbleSort1(int[] array){
if(array==null||array.length==0||array.length==1) return;
for (int i = array.length-1; i >0 ; i--) {
// 判断有无进行交换
boolean work=false;
for (int j = 0; j <i ; j++) {
if(array[j]>array[j+1])
{
swap(array,j,j+1);
work=true;
}
}
if(!work){
break;
}
}
}
/**
* 将数组i j位置进行交换
* @param arr
* @param i
* @param j
*/
public void swap(int[] arr,int i,int j)
{
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}
2、插入排序(稳定)
| 性能 | 值 |
|---|---|
| 时间复杂度 | O(n^2) |
| 最好时间复杂度 | O(n) |
| 最坏时间复杂度 | O(n^2) |
| 空间复杂度 | O(1) |
| 稳定性 | 稳定 |
package ArrraySort;
/***
* 插入排序:
* 时间复杂度:O(n^2)
* 最好时间复杂度:O(n)
* 最坏时间复杂度:O(n^2)
* 空间复杂度:O(1)
* 稳定性:稳定
*/
public class InsertSort {
/***
* 插入排序
*/
public void insertSort(int[] arr)
{
if(arr==null||arr.length==0||arr.length==1) return;
for (int i = 1; i <arr.length ; i++) {
for (int j = i; j >0&&arr[j]<arr[j-1] ; j--) {
swap(arr,j,j-1);
}
}
}
/**
* 将数组i j位置进行交换
* @param arr
* @param i
* @param j
*/
public void swap(int[] arr,int i,int j)
{
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}
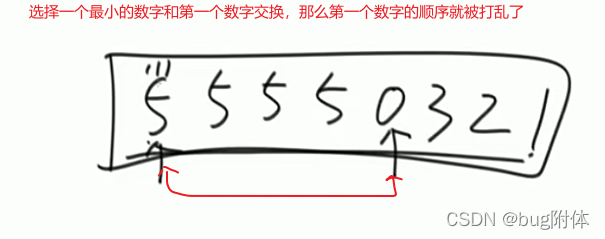
3、选择排序(不稳定)
时间复杂度:O(N^2)
空间复杂度:O(1)
package ArrraySort;
public class SelectSort {
public void selectSort(int[]arr){
if(arr==null||arr.length<2) return;
// N-1次将后面数组的最小值放到数组前面
for (int i = 0; i <arr.length-1 ; i++) {
//记录数组i-N-1中的最小值下标
int index=i;
for (int j = i+1; j <arr.length ; j++) {
if(arr[j]<arr[index]){
index=j;
}
}
swap(arr,i,index);
}
}
/**
* 将数组i j位置进行交换
* @param arr
* @param i
* @param j
*/
public void swap(int[] arr,int i,int j)
{
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}
4、归并排序(稳定)
| 性能 | 值 |
|---|---|
| 时间复杂度 | O(N*logN) |
| 空间复杂度 | O(N) |
| 稳定性 | 稳定 |
归并排序时间复杂度可以达到O(1),但是是论文级别的,内部缓存法
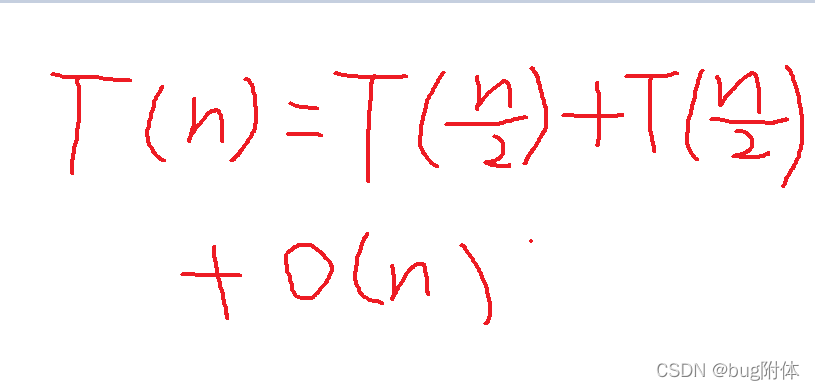
对于公式:

所以在归并排序中,算法时间复杂度是 O(N*logN)
代码:递归实现
package ArrraySort;
/***
* 归并排序:
* 时间复杂度:
*/
public class MergeSort {
/***
* 将数组在L到R范围的排好序
* @param arr
* @param L
* @param R
*/
public void mergeSort(int[]arr,int L,int R){
if(L==R) return;
int mid=L+(R-L)>>1;
mergeSort(arr,L,mid);
mergeSort(arr,mid+1,R);
processSort(arr,L,mid,R);
}
/***
* 将数组在L-mid和mid+1-R中已经排好序的两个数组再合并
* @param arr
* @param L
* @param mid
* @param R
*/
public void processSort(int[] arr,int L,int mid,int R){
// 数组长度
int length=R-L+1;
int i=0;
int l=L;
int r=mid+1;
int[] temp=new int[length];
while(l<=mid&&r<=R){
temp[i++]=arr[l]<arr[r]?arr[l++]:arr[r++];
}
while(l<=mid){
temp[i++]=arr[l++];
}
while(r<=R){
temp[i++]=arr[r++];
}
for (int j = 0; j <length ; j++) {
arr[L++]=temp[j];
}
}
}
代码:非递归实现
/***
* 归并排序的非递归版本
* @param arr
*/
public void mergeSort2(int[]arr){
if(arr==null||arr.length<2)return;
//归并每一步的步长
int step=2;
//归并数组的大小小于数组的大小
while(step< arr.length){
//归并数组的起始
int L=0;
int R=L+step-1;
int mid=L+(R-L)/2;
while (R<arr.length){
processSort(arr,L,mid,R);
//重新进行排序数组的下标变换
L=L+step;
R=L+step-1;
mid=L+(R-L)/2;
}
//将最后越界范围的数组进行排序
mid=L+step/2-1;
R=arr.length-1;
if(mid<R){
processSort(arr,L,mid,R);
}
step=step*2;
}
processSort(arr,0,step/2-1,arr.length-1);
}
题目:返回数组对应位置前面所有比该位置小的和

暴力破解法:时间复杂度O(N^2)
代码:
/***
* 返回数组所有位置前面比它小的数之和
* 暴力破解法:O(N^2)
* @param arr
* @return
*/
public int front_lessNumSum(int[]arr){
if(arr==null||arr.length<2) return 0;
int sum=0;
for (int i = 0; i <arr.length ; i++) {
sum=sum+index_lessNum(arr,i);
}
return sum;
}
public int index_lessNum(int[]arr,int index){
int sum=0;
for (int i = 0; i <index ; i++) {
if(arr[i]<arr[index]) sum+=arr[i];
}
return sum;
}
归并排序改良:
时间复杂度:O(N*logN)
/***
* 通过改良归并排序来实现上述问题的快速求解
* 时间复杂度:O(N*logN)
* @param arr
* @return
*/
public int mergeSolve(int[]arr){
return mergeSort(arr,0,arr.length-1);
}
public int mergeSort(int[]arr,int L,int R)
{
if(arr==null||arr.length<2) return 0;
if(L==R) return 0;
int mid=L+(R-L)/2;
int sum= mergeSort(arr,L,mid)+mergeSort(arr,mid+1,R)+solvePartition(arr,L,mid,R);
processSort(arr,L,mid,R);
return sum;
}
private int solvePartition(int[] arr, int l, int mid, int r) {
if(arr==null||arr.length<2) return 0;
//p是左边数组的下标
int p=l;
//q是右边数组的下标
int q=mid+1;
int sum=0;
while(q<=r){
while (p<=mid){
if(arr[p]<arr[q]){
sum+=(r-q+1)*arr[p++];
}else {
break;
}
}
q=q+1;
}
return sum;
}
private void processSort(int[] arr, int l, int mid, int r) {
if(arr==null) return;
int[] temp=new int[r-l+1];
int i=0;
int p=l;
int q=mid+1;
while (p<=mid&&q<=r){
temp[i++]=arr[p]<arr[q]?arr[p++]:arr[q++];
}
while(p<=mid){
temp[i++]=arr[p++];
}
while(q<=r){
temp[i++]=arr[q++];
}
//最后进行数组的整体拷贝
for (int j = 0; j <temp.length; j++) {
arr[l++]=temp[j];
}
}
官方题解
/***
* 官方题解:
* @param arr
* @return
*/
public int mergeSolve2(int[]arr){
return mergeSort2(arr,0,arr.length-1);
}
private int mergeSort2(int[] arr, int L, int R) {
if(arr==null||arr.length<2) return 0;
if(L==R) return 0 ;
int mid=L+(R-L)/2;
return mergeSort2(arr,L,mid)+mergeSort2(arr,mid+1,R)+processSort2(arr,L,mid,R);
}
/***
* 官方题解
* @param arr
* @param l
* @param mid
* @param r
* @return
*/
private int processSort2(int[] arr, int l, int mid, int r) {
if(arr==null) return 0;
int[] temp=new int[r-l+1];
int res=0;
int i=0;
int p=l;
int q=mid+1;
while (p<=mid&&q<=r){
res+=arr[p]<arr[q]?arr[p]*(r-q+1):0;
temp[i++]=arr[p]<arr[q]?arr[p++]:arr[q++];
}
while(p<=mid){
temp[i++]=arr[p++];
}
while(q<=r){
temp[i++]=arr[q++];
}
//最后进行数组的整体拷贝
for (int j = 0; j <temp.length; j++) {
arr[l++]=temp[j];
}
return res;
}
5、快速排序(不稳定)
| 性能 | 值 |
|---|---|
| 时间复杂度 | O(N*logN) |
| 空间复杂度 | O(logN) |
| 稳定性 | 不稳定 |
5.1简单将一个数组按照数组的最后一个数字将数组中的数字划分为小于等于该数放左边,大于该数放右边,该数放在两者之中
/***
* nov1
* 简单将一个数组按照数组的最后一个数字将数组中的数字划分为小于等于该数放左边,
* 大于该数放右边,该数放在两者之中
* @param arr
* @param L
* @param R
* @return
*/
public void partition1(int[] arr,int L,int R)
{
if(arr==null||arr.length<2||L==R) return ;
//进行小于某个数的放在左边,大于的放在右边,等于的放在中间
int p=-1;
for (int i = 0; i <arr.length ; i++) {
if(arr[i]<=arr[R]){
swap(arr,++p,i);
}
}
}
5.2简单将一个数组按照数组的最后一个数字将数组中的数字划分为小于该数放左边,等于放在中间,大于该数放右边,该数放在两者之中
/***
* 简单将一个数组按照数组的最后一个数字将数组中的数字划分为小于该数放左边,等于放在中间,大于该数放右边,该数放在两者之中
* @param arr
* @param L
* @param R
* @return 返回[0]是L-【0】是小于的部分 【1】-R是大于的部分 【0】+1-【1】-1是等于的部分
*/
public int[] partition2(int[] arr,int L,int R){
if(arr==null||arr.length<2) return null;
//保留下来划分数
int temp=arr[R];
int index=0;
int p=-1;
int q=R+1;
while(index<q){
if(arr[index]<temp){
swap(arr,++p,index++);
}else if(arr[index]>temp){
swap(arr,--q,index);
}else {
index++;
}
}
int[] result={p,q};
return result;
}
public void swap(int[]arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
5.3 快速排序实现思想
·······递归选择某个数,进行左右划分
package ArrraySort;
public class QucikSort {
/***
* 快速排序
* 思想:随机选取数组中的一个数字num,以此为分界线,小于这个数num放在左边,大于num放在右边
* 递归循环往下
* @param arr
*/
public void quickSort(int[]arr,int L,int R){
if(arr==null||arr.length<2) return;
if(L<R){
//随机选择一个数,进行快排的分界数
int num=L+(int)(Math.random()*(R-L+1));
swap(arr,num,R);
int[]result= partition2(arr,L,R);
quickSort(arr,L,result[0]);
quickSort(arr,result[1],R);
}
}
/***
* nov1
* 简单将一个数组按照数组的最后一个数字将数组中的数字划分为小于等于该数放左边,
* 大于该数放右边,该数放在两者之中
* @param arr
* @param L
* @param R
* @return
*/
public int partition1(int[] arr,int L,int R)
{
if(arr==null||arr.length<2||L==R) return L ;
//进行小于某个数的放在左边,大于的放在右边,等于的放在中间
int p=-1;
for (int i = 0; i <arr.length ; i++) {
if(arr[i]<=arr[R]){
swap(arr,++p,i);
}
}
return p;
}
/***
* 简单将一个数组按照数组的最后一个数字将数组中的数字划分为小于该数放左边,等于放在中间,大于该数放右边,该数放在两者之中
* @param arr
* @param L
* @param R
* @return 返回[0]是L-【0】是小于的部分 【1】-R是大于的部分 【0】+1-【1】-1是等于的部分
*/
public int[] partition2(int[] arr,int L,int R){
if(arr==null||arr.length<2) return null;
//保留下来划分数
int temp=arr[R];
int index=0;
int p=-1;
int q=R+1;
while(index<q){
if(arr[index]<temp){
swap(arr,++p,index++);
}else if(arr[index]>temp){
swap(arr,--q,index);
}else {
index++;
}
}
int[] result={p,q};
return result;
}
public void swap(int[]arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}
5.4 快速排序中,时间复杂度和随机选择的数字有关
最坏时间复杂度:如果刚刚好随机选择的数字都是最大的,或者最小的,那么其时间复杂度是0(N^2)
最好时间复杂度:若随机选择的数字刚刚好在中间,那么就是最好的情况,类似于归并排序,时间复杂度是0(NlogN)
长期期望时间复杂度:随机选择快速排序,均值为O(NlogN)
工程上最长使用:因为虽然它的最坏时间复杂度不好,但是它的常数项低,代码量少
5.5 题目:将奇数放在左边,偶数放在右边,空间复杂度O(1),并且保持奇数和偶数稳定
解题思路:快排的一次partition,但是快排是不稳定的,这道题相当于在问你快排怎么实现成稳定的版本,是论文级别的(0-1stableSort)
6、堆排序(堆结构太重要了)
| 性能 | 值 |
|---|---|
| 时间复杂度 | O(N*logN) |
| 空间复杂度 | O(1) |
堆结构是一颗完全二叉树
完全二叉树是什么?
二叉树是从左到右排序的,并且一层排满再到另一排
是:

不是:
将完全二叉树表示成数组形式:
第i个节点:
其左子元素是:2*i+1
右子元素:2*i+2
其父元素:(i-1)/2
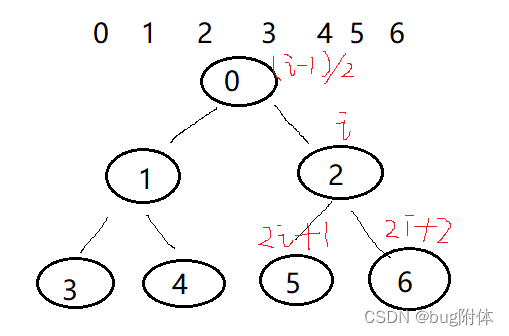
6.1 堆排序的分类:
大根堆:每颗子树的父节点都大于这颗子树下面的所有结点
小根堆:每颗子树的父节点都小于这颗子树下面的所有结点
6.1.1 堆的建立
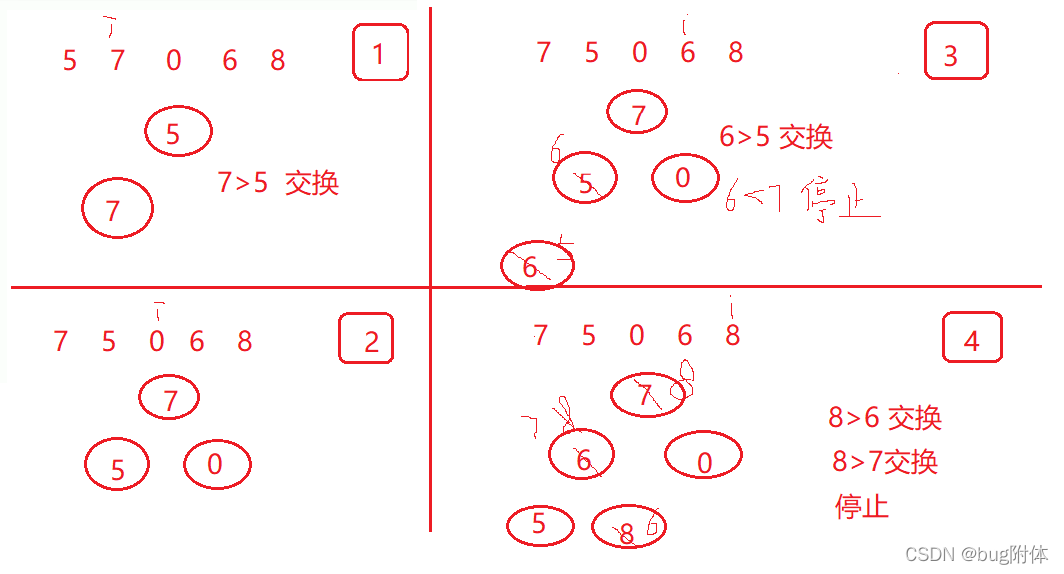
时间复杂度:
log1+log2+…+logN=O(N)
/***
* 在建立堆的时候,进行上升判断,如果index比父节点大,那么交换位置
* @param arr
* @param index
*/
public void heapInsert(int[] arr,int index){
if(arr==null||arr.length<2||index>=arr.length||index<=0) return;
//计算父节点的位置
while (arr[index]>arr[(index-1)/2]){
swap(arr,index,(index-1)/2);
index=(index-1)/2;
}
}
6.1.2 堆排序需要的将0位置和最后一个交换后,0位置上的数往下降
/***
* 堆从根头往下冒
* @param arr
* @param index
* @param heapSize
*/
public void heapify(int[]arr,int index,int heapSize){
if(arr==null||arr.length<2||index<0||index>=heapSize)return;
int left=index*2+1;
while (left<heapSize){
//将左右子数的最大的那个下标返回
int right=index*2+2;
int largest=right<heapSize&&arr[right]>arr[left]?right:left;
if(arr[index]<arr[largest]){
swap(arr,index,largest);
index=largest;
left=index*2+1;
}else {
break;
}
}
}
6.1.3 堆排序(依次到size=0)
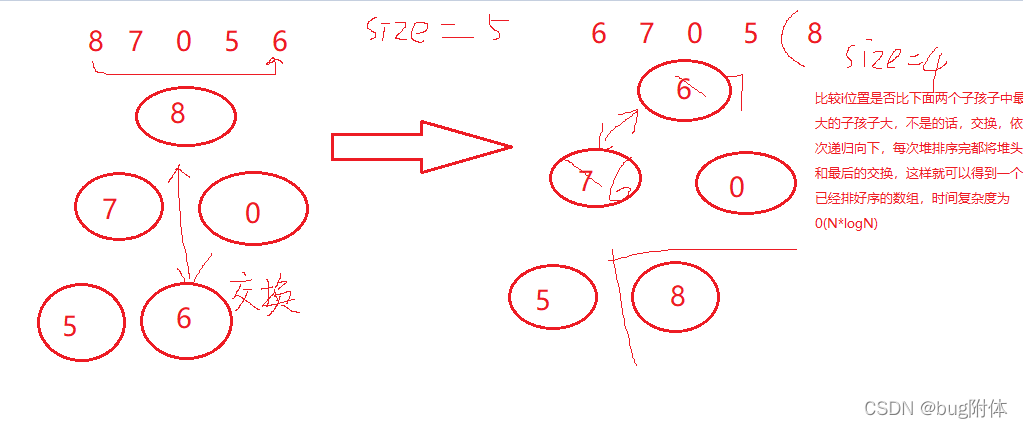
时间复杂度:O(N*logN)
工程上不经常用这个的原因:常数项太复杂,而且不稳定
package ArrraySort;
/***
* 大根堆排序
* 时间复杂度:O(N*logN)
* 空间复杂度:O(1)
*/
public class HeapSort {
public void heapSort(int[]arr){
if(arr==null||arr.length<2)return;
//首先进行堆排序
for (int i = 0; i <arr.length ; i++) {
heapInsert(arr,i);
}
//堆排序之后,将最大值和堆的最后元素交换,然后缩小堆的大小,把刚刚交换后的第一个元素进行由上到下的堆调整,依次下去,直到堆0
int heapSize=arr.length;
swap(arr,0,heapSize-1);
heapSize--;
while (heapSize>0){
heapify(arr,0,heapSize);
swap(arr,0,heapSize-1);
heapSize--;
}
}
/***
* 在建立堆的时候,进行上升判断,如果index比父节点大,那么交换位置
* @param arr
* @param index
*/
public void heapInsert(int[] arr,int index){
if(arr==null||arr.length<2||index>=arr.length||index<=0) return;
//计算父节点的位置
while (arr[index]>arr[(index-1)/2]){
swap(arr,index,(index-1)/2);
index=(index-1)/2;
}
}
/***
* 堆从根头往下冒
* @param arr
* @param index
* @param heapSize
*/
public void heapify(int[]arr,int index,int heapSize){
if(arr==null||arr.length<2||index<0||index>=heapSize)return;
int left=index*2+1;
while (left<heapSize){
//将左右子数的最大的那个下标返回
int right=index*2+2;
int largest=right<heapSize&&arr[right]>arr[left]?right:left;
if(arr[index]<arr[largest]){
swap(arr,index,largest);
index=largest;
left=index*2+1;
}else {
break;
}
}
}
/***
* 交换数组中的两个位置
* @param arr
* @param i
* @param j
*/
public void swap(int[]arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
}
7、在java中系统排序
Arrays.sort(T[]arr);
size<=60:用插入排序
size>60:会先进行归并或者快排,将数组的大小缩小到60之后,然后用插入排序
那么选择用归并还是快排呢?取决于元素的类型:
若元素是int double char等基础类型,那么采用快排
若元素是对象,那么采用归并,这是因为稳定性的原因
四、对数器的实现
作用:对数器是用来干什么的呢?
简单来说,对数器就是用来验证我们写完代码的准确性的。
在工程中,我们总会实现时间复杂度和空间复杂度更低的代码,但是这些代码没办法保证一定准确,这时候我们就需要通过一定的随机测试数据来通绝对正确的方法和我们打出的方法进行对比,依次来验证我们打出代码的正确性
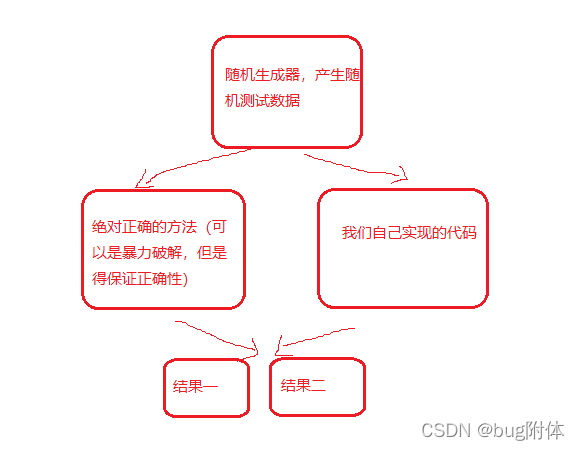
拿冒泡排序来举例子:
import ArrraySort.BubbleSort;
import ArrraySort.InsertSort;
import ArrraySort.MergeSort;
import ArrraySort.SelectSort;
import exercise.FindSameWord;
import org.junit.Test;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Arrays;
public class testMachine {
//排序的对数器
@Test
public void selectTest(){
int times=50000;//比较的次数
int size=1000;//数组的可能长度
int value=10000;//数组的取值范围
for (int i = 0; i <times ; i++) {
int[] arr = generateRandomArray(size, value);
// int[] arr={2,5,3,6,8,34,45};
int[] arr2=copyArray(arr);
//自定义函数进行冒泡排序
SelectSort selectSort=new SelectSort();
selectSort.selectSort(arr);
//调用肯定正确的方法
rightMethod(arr2);
//比较结果是否正确
if(!isEqual(arr,arr2)){
System.out.println("排序结果错误");
break;
};
}
System.out.println("排序结果正确");
}
@Test
public void mergeTest(){
int times=5000;//比较的次数
int size=10000;//数组的可能长度
int value=10000;//数组的取值范围
for (int i = 0; i <times ; i++) {
int[] arr = generateRandomArray(size, value);
// int[] arr={2,5,3,6,8,34,45};
int[] arr2=copyArray(arr);
//自定义函数进行冒泡排序
MergeSort mergeSort=new MergeSort();
mergeSort.mergeSort(arr,0,arr.length-1);
//调用肯定正确的方法
rightMethod(arr2);
//比较结果是否正确
if(!isEqual(arr,arr2)){
System.out.println("排序结果错误");
break;
};
}
System.out.println("排序结果正确");
}
@Test
public void insertTest()
{
int times=500000;//比较的次数
int size=1000;//数组的可能长度
int value=10000;//数组的取值范围
for (int i = 0; i <times ; i++) {
int[] arr = generateRandomArray(size, value);
int[] arr2=copyArray(arr);
//自定义函数进行冒泡排序
InsertSort insertSort=new InsertSort();
insertSort.insertSort(arr);
//调用肯定正确的方法
rightMethod(arr2);
//比较结果是否正确
if(!isEqual(arr,arr2)){
System.out.println("排序结果错误");
break;
};
}
System.out.println("排序结果正确");
}
@Test
public void bubbleTest()
{
int times=10000;//比较的次数
int size=1000;//数组的可能长度
int value=10000;//数组的取值范围
for (int i = 0; i <times ; i++) {
int[] arr = generateRandomArray(size, value);
for (int j = 0; j <arr.length ; j++) {
System.out.print(arr[j]+" ");
}
int[] arr2=copyArray(arr);
//自定义函数进行冒泡排序
BubbleSort bubbleSort=new BubbleSort();
bubbleSort.bubbleSort1(arr);
//调用肯定正确的方法
rightMethod(arr2);
//比较结果是否正确
if(!isEqual(arr,arr2)){
System.out.println("排序结果错误");
break;
};
}
System.out.println("排序结果正确");
}
/**
* 数组拷贝
* @param arr
* @return
*/
public int[] copyArray(int[] arr){
int[] arr2=new int[arr.length];
for (int i = 0; i <arr.length ; i++) {
arr2[i]=arr[i];
}
return arr2;
}
/**
* 正确的方法:返回绝对正确的排序数组
* @param arr
*/
public void rightMethod(int[] arr){
Arrays.sort(arr);
}
/**
* 产生随机测试的数组
* @param size 产生的数组大小0-size
* @param value 数组的范围取值
* @return
*/
public int[] generateRandomArray(int size,int value){
int[] arr=new int[(int)(Math.random()*(size+1))];
for (int i = 0; i <arr.length ; i++) {
arr[i]=(int)((Math.random()*value+1)-(Math.random()*(value)));
}
return arr;
}
/**
* 判断两个数组是否相等
* @param arr 待判断的数组1
* @param arr2 待判断的数组2
* @return 比较的结果
*/
public boolean isEqual(int[]arr,int[]arr2){
if(arr==null&&arr2==null) return true;
if(arr==null||arr2==null) return false;
if(arr.length!=arr2.length) return false;
for (int i = 0; i <arr.length ; i++) {
if(arr[i]!=arr2[i]){
return false;
}
}
return true;
}
}
总结
在上诉过程中,我们了解且实现了各种各样的排序算法,下面我们将接着学习