[数据结构与算法]狂刷力扣 *第189题轮转数组题解

针对这道题我有两种思路

解法一：

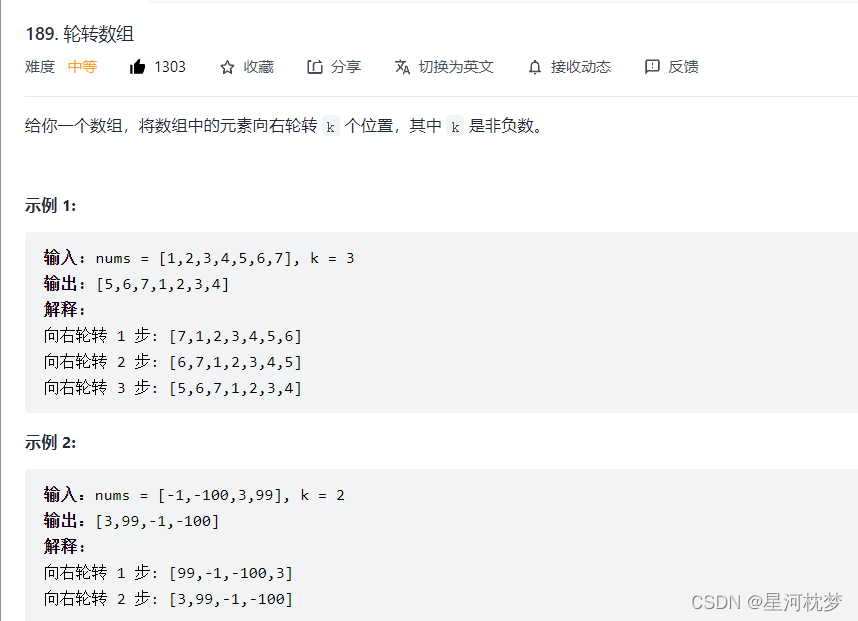
遍历轮转，新开辟一个中间变量temp，用于存放nums[numsSize-1],之后开始遍历数组进行交换.实现代码如下

void rotate(int* nums, int numsSize, int k)
{
    int temp = 0;
    int i = 0;
    int numsS=numsSize;//储存数据
    if (k > numsSize)
    {
        k = k % numsSize;//轮转k次相当于轮转了一周，省去计算冗余
    }
    for(i=0;i<k;i++)
    {
     temp = nums[numsSize - 1];//更新数组末值
     while (numsSize-1)
    {
        nums[numsSize - 1] = nums[numsSize - 2];
        numsSize--;
    }
    nums[0] = temp;
    numsSize =numsS;//重置数据，方便下次循环
   }
}

虽然实现了目的，但是这个算法实际上还不够好，它的时间复杂度竟然达到了

O(k*n),数据如果少还可以蒙混过关，但是这样不行

?你看，就连力扣都觉得这样不行，所以我们要进行算法优化。

解法二：

先把后k项逆置，再逆置前numsSize-k项，再将数组整体逆置。

void Revise(int* nums, int left, int right)//逆置函数
{
    int temp = 0;
    while (right > left)
    {
        temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
        right--;
        left++;
    }
}
void rotate(int* nums, int numsSize, int k)
{
    if (k > numsSize)
    {
        k = k % numsSize;
    }
    Revise(nums, numsSize - k, numsSize - 1);//后k项逆置
    Revise(nums, 0, numsSize - k - 1);//前numsSize-k项逆置
    Revise(nums, 0, numsSize - 1);//数组整体逆置

这样一步到位，算法的时间复杂度为O(n),相比上面那个算法要好得多。

需要注意的是，Revise函数使用时，需要框好数组的范围，在评价一个算法的好坏时，善于利用时间复杂度，空间复杂度的思想。