第2.2讲 空间解析几何中的平面和直线
本节中将利用向量运算的方法,给出几何中基础的平面和直线表达。用代数的方法给出几何关系,这是空间解析几何的特点。向量的方法给出几何变量之间的关系,和纯几何方法不同,更加简单直接。
学习要点
1、利用数量积和向量积的代数方法表示平面和直线方程,快速解决几何问题
2、用数量积为0表示直线(向量)垂直,用于平面内直线和法向量的关系,可用来表示平面点法式方程
3、通过平面内两个直线向量的向量积来表示法向量
一、平面方程
我们知道,三点确定一个平面,一个点和法向量也能确定一个平面。采用向量计算的方法,可以很恰当地描述这些几何关系。向量积给出了法向量的计算方法,数量积给出向量垂直的关系。灵活地应用数量积、向量积,可以快速地给出平面方程。
1、平面方程
(1)点法式方程(向量积+数量积)和一般方程(法向量提取)
用平面内点写出平面内直线向量,用其中两个平面向量的向量积给出法向量表示,然后利用平面直线向量与法向量垂直的数量积形式,给出点法式方程。简单明了,这就是解析几何的魅力。




(2)三点式方程形式(混合积)



(3)截距方程形式

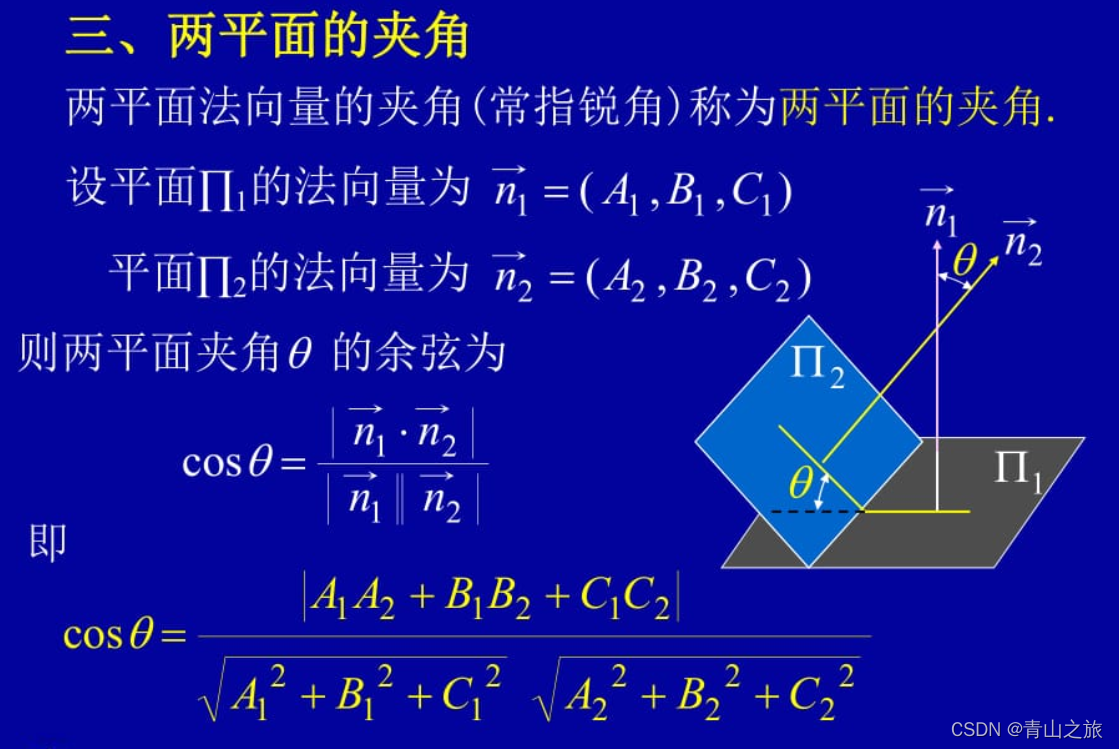
2、平面夹角(法向量夹角用数量积求取)

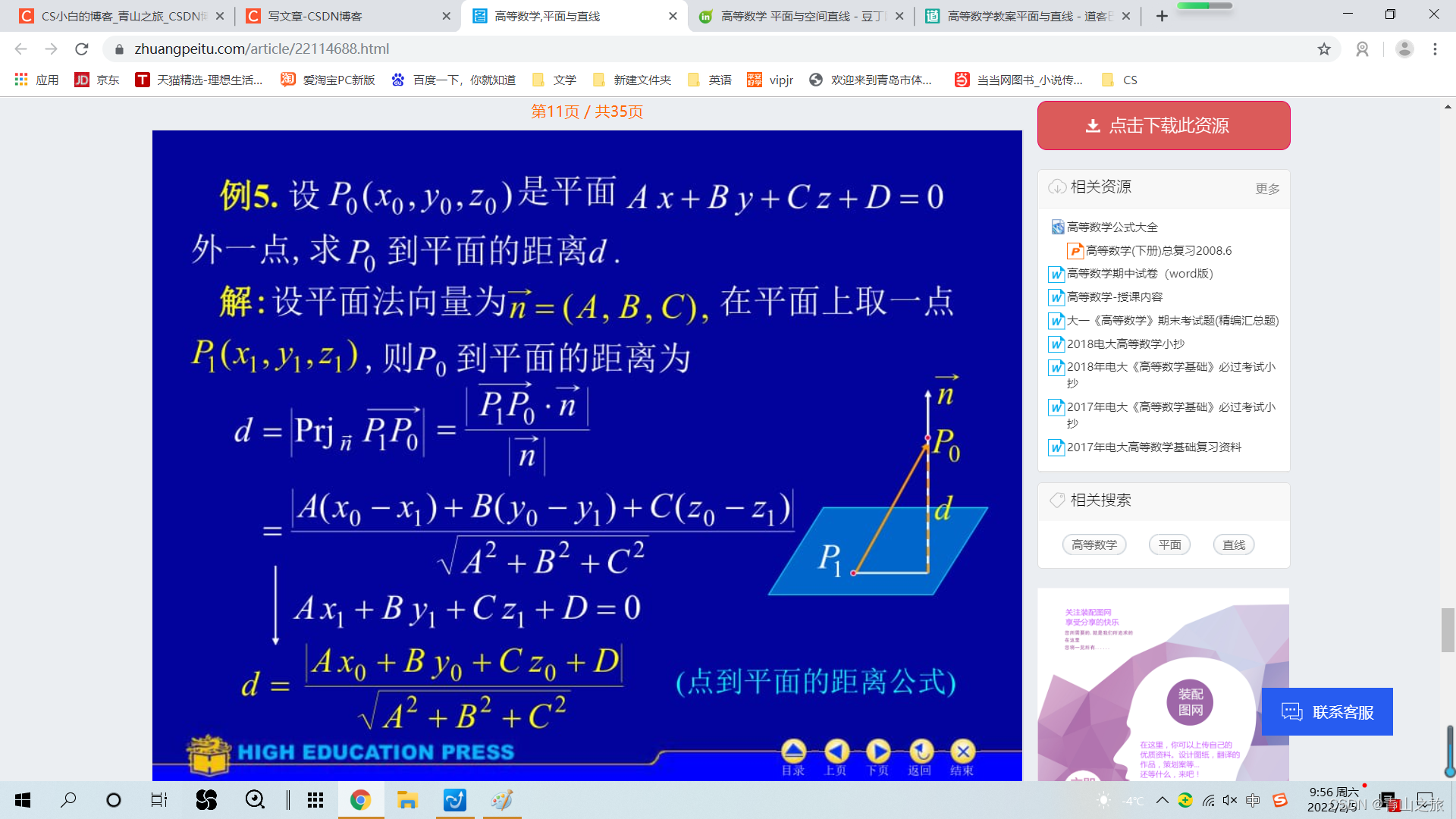
3、点到平面距离