开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 二分图全解 -> 正文阅读

[数据结构与算法]二分图全解

算法思想

二分图的定义：如果一个图的所有顶点可以分为 $X$ 和 $Y$ 两个集合，且对于所有边来说，边的两点都不属于同一集合，那么这个图就是二分图

更准确的定义如下：
$G = (V, E)$ 为无向图， $V$ 为点集， $E$ 为边集，如果 $V$ 可被分割成两个互不相交的子集 $V_1,V_2)$ ，且图中每条边 $(i, j)$ 两端点分别属于这两个子集，则称 $G$ 为一个二分图

二分图的相关概念如下：

匹配：一个只有边的集合，集合中任意两条边无公共点，在一个图的所有匹配中，边数最多的匹配叫做该图的最大匹配
独立集：两两互不相连的节点集合
边覆盖：任意节点都至少是某条边端点的边集合，也就是不存在孤立点
点覆盖：任意边都至少有一个点的点集合，即不存在孤立边
最小路径覆盖：在一个DAG中，如果存在一个简单路集合（顶点不相交），图的每个顶点都在路上，则该路为一个路径覆盖，最小路径覆盖为所含路径条数最少的路径覆盖

二分图染色

对于给定的一个图，首先需要判断它是否为二分图才能进行相关操作，对于一个无向图来说，当且仅当不存在有奇数条边构成的环时，它才是二分图，这是充要条件，举个例子简单证明

如图，当为奇数环时，根据二分图的定义，可以看到？处无法被赋值

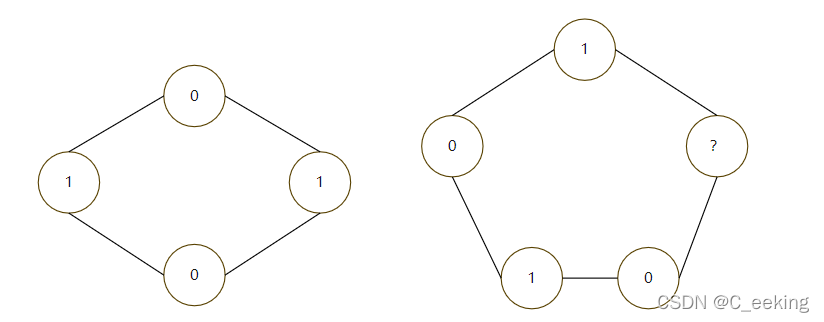
在这里插入图片描述
根据二分图的性质可以知道，所有的点被分成了两个集合，那么相连的两个点必然不属于同一集合，因此，可以从任意一点开始，将其设置为1，其邻接点必然为0，以此类推，如果最后出现无法赋值的点，那么必然不是二分图，可以用DFS实现

代码

bool DFS(int u,int c)
{
		col[u]=c;
		for(int i=head[u];~i;i=e[i].next)
		{
				int v=e[i].to;
				if(col[v]==col[u])return 0;
				if(col[v]==-1&&!DFS(v,!col[u]))return 0;
		}
		return 1;
}

当然，如果给的图不是连通图，那么就需要对每个未遍历点进行判断

for(int i=1;i<=n;i++)
	if(col[i]==-1)if(!DFS(i,1))return 0;

二分图相关定理

K?nig: 最小点覆盖=二分图最大匹配
二分图最小边覆盖: 顶点数-二分图最大匹配
最小路径覆盖: 顶点数-二分图最大匹配数
最大独立集: 总点数-二分图最大匹配数

求出最小路径覆盖集合只需要沿着增广路输出即可，输出所有的匹配路

代码

void print(int u)
{
	u+=n;//初始化
	do
		printf("%d ",u=u-n);
	while(vis[u]=1,u=match[u]);
}
for(int i=1;i<=n;i++)
	if(!vis[i])print(i);

最小可相交路径覆盖：Floyd求原图传递闭包

最大匹配算法

首先说明最大匹配的概念，最大匹配指的是在二分图中包含边数最多的一组匹配，是二分图的一类问题，如图，给出了可匹配的关系，求最大匹配可以将原图转换为最大流问题，添加源点和汇点，边权设为1，然后直接跑最大流即可，时间复杂度为 $O(V^2E)$ ，但是，给出的图是二分图，可以利用二分图的性质求解，下面为用二分图性质求解的匈牙利算法和KM算法
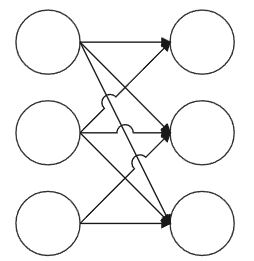
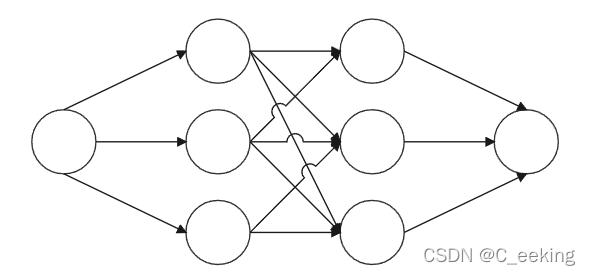
在这里插入图片描述

匈牙利算法

首先给出交替路和增广路概念
交替路：从一个未匹配点出发，依次经过非匹配边，匹配边，非匹配边，…形成的路径为交替路
增广路：从一个未匹配点出发，走交替路，如果途径另一个与起点不同的未匹配点，则这条交替路则称为增广路
注意二分图与求解最大流中的增广路定义不同
给出一个例子进行简单的算法思路说明，这是一个简单的图例，给出了可匹配关系，从节点1开始寻找可匹配点，1可以找到4，之后2再找可匹配点5
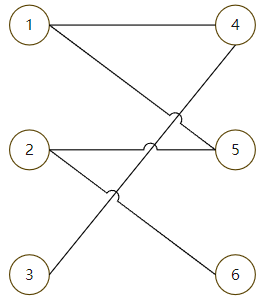
在这里插入图片描述
但是对于节点3，它的唯一可匹配点只有4，4此时已经和1匹配，那么尝试将1与其他的节点匹配

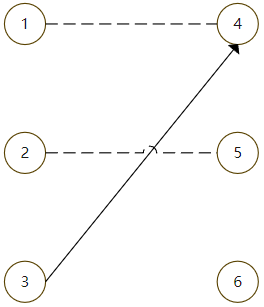
在这里插入图片描述
1可以与5匹配，但是5已经与2匹配，那么尝试将2与其他的节点匹配

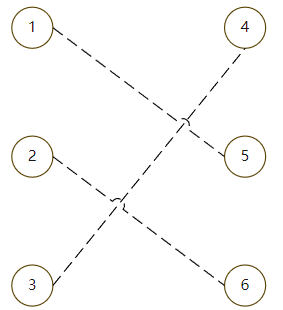
2可以与6匹配，所以最后就可以得到最大匹配的结果

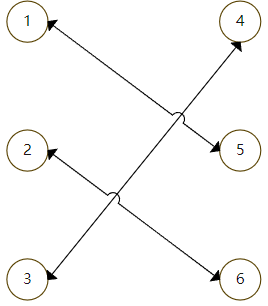
这就是匈牙利算法基本思路，根据概念来看，增广路的存在代表可以通过修改当前匹配来增加新的匹配，增广路的本质就是一条路径的起点和终点都是未配对的点，在上述过程中，匹配关系有时需要更改，从已匹配变成未匹配，这个操作被称为“反色”，易证“反色”后的匹配仍然合法且大于等于原匹配

算法步骤：

初始化节点，从左集合中首个点$$开u始检查
检查 $u$ 的邻接点 $v$ ，若 $v$ 未匹配，直接匹配两点，否则从 $v$ 的邻接点出发找增广路，存在增广路就更新匹配关系，即反色，然后匹配 $u, v$
找不到最大匹配，即可得到一个最大匹配

代码

bool maxmatch(int u) {//传入左集合节点
    for(int i=head[u]; ~i; i=e[i].next) {//BFS
        int v=e[i].to;
        if(!vis[v]) {//如果没访问过
            vis[v]=1;
            if(!match[v]||maxmatch(match[v]))//如果可以匹配
            {
                match[v]=u;//设定匹配
                return 1;
            }
        }
    }
    return 0;
}

KM算法

KM算法的目的是求出二分图的最大权完美匹配，也就是二分图的两个点集大小需要相同，一般来说，二分图不可能保证两边一定大小相同，所以需要将个数少的一边补点，再将不存在的边权设为0

接下来是与KM相匹配的概念与定理

可行顶标： 给每个节点有个点权 $f (i)$ ，对于所有的边 $u ? v$ ，满足所有的边权 $w(u,v)\le f(u)+f(v)$

相等子图： 在一组可行顶标下原图的生成子图，包含所有点但只满足 $w (u, v) = f (u) + f (v)$ 的边 $u ? v$

如果相等子图有完美匹配，则其必然为原图的最大权完美匹配

根据定理，求解最大权完美匹配过程中，需要不断调整可行顶标，使得相等子图拥有完美匹配

一开始不可能直接确定好所有的顶标，所以需要反复确认，修改顶标，当一条边满足 $w (u, v) = f (u) + f (v)$ ，代表其为相等子图的一条边，将其加入图中

设二分图左点集合顶标为 $l (i)$ ，右集合顶标为 $r (i)$ ，初始化时，因为可行顶标需要满足点权和大于等于边权，不妨设 $l (i)$ 全部为0， $r (i)$ 为对应点所连的边权最大值

调整顶标过程中，目的是构造一个相等子图，也就是不断的向原先构造的子图中添加新边，使得 $l (i) + r (j) = w (i, j)$ ，那么在初始化之后，需要找到一条边 $u ? v$ 使得 $u$ 不在二分图最大匹配中，而 $v$ 在二分图最大匹配中（u点权为0，v点权为最大边权，为了获得最大匹配，默认以v为基准匹配）

对于这样的一条边，我们希望将其加入正在构造的相等子图，就要使得边满足条件，那么顶标和需要减少 $△ x = l (u) + r (v) ? w (u, v)$

因为默认 $v$ 在最大匹配中，改变其点权会影响其他的边（比如边权最大的那条边，如果 $v$ 点权变了，那么边权最大的那条边的两端点可能就不满足可行顶标的定义了），所以只对 $u$ 进行操作，也就是 $l (u) + △ x$ 或者 $r (u) ? △ x$ （ $u$ 不一定就在左边），为了放置修改完导致部分顶标不符合定义，所以每次找的 $△ x$ 尽量小

代码（假 $O(n^3)$ ）

bool maxmatch(int u) {
    visr[u]=1;//
    for(int i=1; i<=n; i++) {
        if(visl[i])continue;
        int d=l[i]+r[u]-gragh[u][i];//获得缺的值
        if(d==0) {//代表这条边已经满足了相等子图的条件
            visl[u]=1;//代表可能可以产生匹配
            if(!match[i]||maxmatch(match[i])) {
                match[i]=u;
                return 1;
            }
        } else delta[i]=min(delta[i],d);//更新最小差值
    }
    return 0;
}
int KM() {
    memset(match,0,sizeof(match));//清空匹配
    memset(l,0,sizeof(l));//清空左部点集
    for(int i=1; i<=n; i++) {//初始化右部顶标，默认为边权最大
        r[i]=gragh[i][1];
        for(int j=2; j<=n; j++)
            r[i]=max(r[i],gragh[i][j]);
    }
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=n; j++)delta[j]=inf;
        while(1) {
            memset(visl,0,sizeof(visl));//清空访问
            memset(visr,0,sizeof(visr));//同上
            if(maxmatch(i))break;
            //继续进行代表i未收录，未匹配成功，需要调整顶标
            int d=inf;
            for(int j=1; j<=n; j++)
                if(!visl[j])d=min(d,delta[j]);
            //visl[j]为1代表已经在构造的增广路上，已经满足d为0了
            //已经无法再提供可以增加相等子图的差值，重复取会死循环
            for(int j=1; j<=n; j++) {
                //这里能修改，是因为匹配失败了
                //也就是经过的点的顶标并不能满足i在最大匹配内，需要尝试修改
                if(visr[j])r[j]-=d;
                if(visl[j])l[j]+=d;
                else delta[j]-=d;//因为r[j]增加了，差值变小了
            }
        }
    }
    for(int i=1; i<=n; i++)res+=gragh[match[i]][i];//累和匹配边
    return res;
}

二分图匹配的复杂度最差为 $O(n^2)$ （maxmatch函数），而while(1)循环的最多可以到 $O (n)$ （尝试与所有节点进行构造匹配），因此整个算法的复杂度最高可达到 $O(n^4)$

可以发现，在修改边的时候，因为每次DFS的起点相同，所以可能每次只修改了一条边，因此有重复搜索的情况，那么将DFS改成BFS，就可以减少搜索的重复性，减少复杂度

代码（ $O(n^3)$ ）

int pre[maxn],match[maxn],delta[maxn],graph[maxn][maxn],n,m,res,l[maxn],r[maxn];
int a[maxn],p[maxn],b[maxn],c[maxn];
bool visl[maxn],visr[maxn];
void maxmatch(int u) {
    int x,y=0,d,id=0;
    memset(pre,0,sizeof(pre));//pre用来记录上一条边
    for(int i=1; i<=n; i++)delta[i]=inf;//初始化右点集
    match[y]=u;//初始化匹配关系
    while(1) {
        x=match[y];
        d=inf;//初始化
        visr[y]=1;//访问
        for(int i=1; i<=n; i++) {
            if(visr[i])continue;
            if(delta[i]>l[x]+r[i]-graph[x][i]) {//能否加一条边x-i
                delta[i]=l[x]+r[i]-graph[x][i];
                pre[i]=y;//连接一条未匹配边
            }
            if(delta[i]<d) {//找到一条修改值最少的点
                d=delta[i];//记录数值
                id=i;//记录编号
            }
        }
        for(int i=0; i<=n; i++)
            if(visr[i])l[match[i]]-=d,r[i]+=d;//尝试修改
            else delta[i]-=d;//该边不是最短边，减去后可能成为最短边
        y=id;
        if(match[y]==-1)break;//无法继续匹配
    }
    while(y) {//构造匹配
        match[y]=match[pre[y]];
        y=pre[y];
    }
}
int KM() {
    memset(match,-1,sizeof(match));//清空匹配
    memset(l,0,sizeof(l));
    memset(r,0,sizeof(r));
    for(int i=1; i<=n; i++) {
        memset(visr,0,sizeof(visr));
        maxmatch(i);//BFS左点集
    }
    for(int i=1; i<=n; i++)
        if(match[i]!=-1)res+=graph[match[i]][i];
    return res;
}

二分图博弈

二分图博弈为一类博弈模型，与二分图的最大匹配有关，其基本模型如下：给出一张二分图和起点，博弈双方轮流操作，每次只能选择与上次被选择点相邻的点，且不能选择已经访问过的点，无法继续操作者判负

设起点为S，有一个结论：如果二分图的任意一个最大匹配一定有S，即S为最大匹配必须点，那么先手必胜，否则先手必败

下面来证明这个结论
如图，给出了一个最大匹配，假设起点S=1，那么按照策略，先手选择2，此时，后手要么无点可选，要么选3（如果2-3存在的话，之后会证明这一点），又到了先手从3开始选择，可以看到，只要先手一直按照寻找匹配点的策略选下去，到最后总会有后手无点可选

如果起点不属于最大匹配中，先手必输，因为先手从起点的下一步必是图中的匹配点之一（之后证明），那么情况和上一段完全相同，只不过是后手按照匹配点的策略来选，到最后总会使先手无点可选
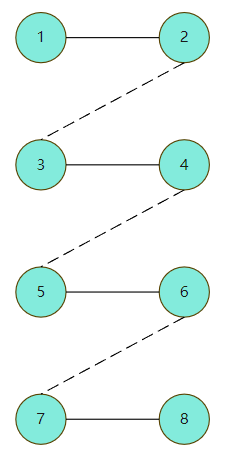
在这里插入图片描述
现在进行更详细的证明，如果最大匹配一定包括S，按照先前所说，后手不可能选到最大匹配之外的点，如图，如果后手可以选到非匹配点，例如图中的9，那么图中的最大匹配方案就不止一个：1-2,3-4,5-6,7-8和1-2,4-9,5-6,7-8都可以作为最大匹配，违背了最大匹配一定包括S
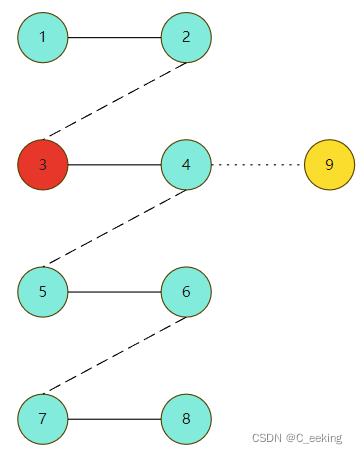
在这里插入图片描述
如果最大匹配不一定包括S，在这种情况下，可能是有唯一最大匹配，但是S并不在最大匹配中，或者S并不是所有最大匹配的必须点，如图，从9开始，先手的下一步必然是匹配点，否则的话

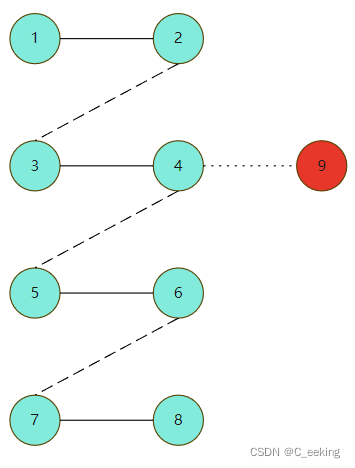
在这里插入图片描述
就会出现下图所属的情况，存在一条边9-10不属于最大匹配，显然，这是不合理的，因为9和10都不属于匹配点，但是它们能够构成匹配，原先的最大匹配就不是最大的了，因此矛盾

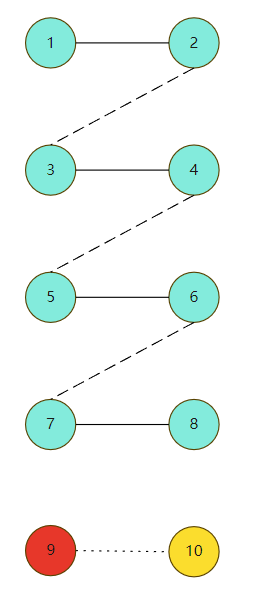
接下来的问题就是如何确定起点是否属于最大匹配，方法很简单，直接对有起点和没有起点的原图做最大匹配，如果匹配数相同，代表起点不一定在最大匹配上，否则一定在最大匹配上，可以采用Dinic和匈牙利求解
跑Dinic时不用根据是否有起点建两次图，而是建图的时候保存涉及起点的边，跑完一次Dinic后再建边，查看Dinic是否增加流量

总结一下，对于二分图博弈，分两种大的情况来考虑（实际上是一种情况，但是这样分开更清晰）

有起点
有起点的情况下，需要判断起点是否一定属于最大匹配，即为最大匹配必须点，如果是，那么先手必胜，否则先手必输
无起点
无起点的情况下，先手需要选择起点，如果先手先选择最大匹配点，后手只需要选择对应的最大匹配的匹配点即可，先手必败，如果图为完全匹配，先手一定会选择最大匹配点，如果不是完全匹配，先手选择非最大匹配点或最大匹配非必须点，那么后手总会首先到最大匹配，所以先手可胜

训练

LuoguP1330

题目大意：略

思路：由题设可知，河蟹之间是不能相连的，那么所有的河蟹可以被划分成两个集合，这恰好符合二分图，那么直接判断给出的图是否是二分图即可，如果不是则无解，若是则选取颜色少的节点，由于题目不保证连通，所以要对每个连通块都进行二分图染色

代码

#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=4e5+10;
int n,m,cnt,res,head[maxn/10],col[maxn/10],dress[2];
struct node {
    int next,to;
} e[maxn<<1];
void Add(int from,int to) {
    e[++cnt].to=to;
    e[cnt].next=head[from];
    head[from]=cnt;
}
bool DFS(int u,int c) {
    col[u]=c;
    dress[c]++;
    for(int i=head[u]; ~i; i=e[i].next) {
        int v=e[i].to;
        if(col[v]==col[u])return 0;
        if(col[v]==-1&&!DFS(v,!col[u]))return 0;
    }
    return 1;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >>n>>m;
    memset(head,-1,sizeof(head));
    memset(col,-1,sizeof(col));
    while(m--) {
        int u,v;
        cin >>u>>v;
        Add(u,v);
        Add(v,u);
    }
    for(int i=1; i<=n; i++)
        if(col[i]==-1) {
            if(!DFS(i,1)) {
                res=0;
                break;
            }
            res+=min(dress[0],dress[1]);
            dress[0]=dress[1]=0;
        }
    res==0? cout <<"Impossible": cout <<res;
    return 0;
}

LuoguP1285

题目大意：略

思路：很重要的一点，如果两个队员不是双向的，那么这两个人一定不能在同一组，因此，在建图的时候，每个点与必不能同一组的点建边，这样的话整个图就可以分成两个点集，也就是二分图，经过染色，整个图也就被分成的多个拥有黑白相间的连通块，显然，每个块只能取全黑或全白，这样的话，整个模型就可以抽象成01背包模型，有k个连通块，每个连通块要么全选黑，要么选白，要求最后分组的差最小，这里的 $d p [i] [j]$ 可以解释为在第i个连通块上，能否选j个人，其余见代码

代码

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
int n,acc[121][2],pre[121][121],res,col[121],block,out[121];
bool gragh[121][121],dp[121][121],mark[121];
vector<int>path[121][2];
void DFS(int u,int f,int c) {
    acc[block][col[u]=c]++;//记录下第block个连通块颜色c的个数
    path[block][c].push_back(u);//记录下第block个连通块颜色c有哪些
    for(int i=1; i<=n; i++)
        if(!gragh[i][u]&&i!=f&&u!=i) {
            if(col[i]==-1)DFS(i,u,c^1);//如果相邻点未染色，取反色
            else if(col[i]==c) {
                cout <<"No solution";
                exit(0);
            }
        }
}
int main() {
    cin >>n;
    memset(col,-1,sizeof(col));
    for(int i=1; i<=n; i++) {
        int k;
        while(cin >>k&&k)gragh[i][k]=1;
    }
    for(int i=1; i<=n; i++)
        for(int j=i+1; j<=n; j++)
            if(gragh[i][j]!=gragh[j][i])gragh[i][j]=gragh[j][i]=0;
    //如果彼此之间不能到达，不连边
    for(int i=1; i<=n; i++)
        if(col[i]==-1) {//没染色
            block++;
            DFS(i,0,1);
        }
    dp[0][0]=1;//初始化
    for(int i=1; i<=block; i++)//多个连通块，可以等价于block个物品
        for(int j=0; j<=n/2; j++) {//容量
            int p=j-acc[i][0];//acc[i][0]为前i个连通块可以拿出0的个数，p为达到j需要的个数
            if(p>=0&&dp[i-1][p])dp[i][j]=1,pre[i][j]=0;
            //如果需要多的0，并且前i-1个块有，代表当前装j个也能满足
            //pre记录先前的转移状态，装的是0
            p=j-acc[i][1];//
            if(p>=0&&dp[i-1][p])dp[i][j]=1,pre[i][j]=1;
            //同上
        }
    for(int i=n/2; i>=0; i--)
        if(dp[block][i]) {//存在一个解使得容量差小
            res=i;
            break;
        }
    int t=res;
    for(int i=block; i>0; i--) {//遍历每个块，回溯求解
        for(int j=0; j<path[i][pre[i][t]].size(); j++)
            //遍历块，将颜色为pre[i][t]的节点录入
            mark[out[++out[0]]=path[i][pre[i][t]][j]]=1;
        t-=acc[i][pre[i][t]];//减去已经使用的块数量
    }
    sort(out+1,out+out[0]+1);//根据题意排序输出
    cout <<out[0]<<" ";
    for(int i=1; i<=out[0]; i++)
        cout <<out[i]<<" ";
    cout <<endl<<n-out[0]<<" ";
    for(int i=1; i<=n; i++)
        if(!mark[i])cout <<i<<" ";
    return 0;
}

POJ1274

题目大意：牛棚与牛直接存在对应关系，每只牛对牛棚有自己的喜好，一个牛棚只能分配给一头牛，一头牛只能分给一个牛棚，计算最多能将牛分配给牛棚多少头

思路：二分图问题，根据对应关系构造二分图然后用匈牙利算法算最大匹配即可

代码

#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=4e4+10;
int n,m,cnt,head[500],match[500];
struct node {
    int next,to;
} e[maxn<<1];
void Add(int from,int to) {
    e[++cnt].to=to;
    e[cnt].next=head[from];
    head[from]=cnt;
}
bool vis[500];
bool maxmatch(int u) {//传入左集合节点
    for(int i=head[u]; ~i; i=e[i].next) {//BFS
        int v=e[i].to;
        if(!vis[v]) {//如果没访问过
            vis[v]=1;
            if(!match[v]||maxmatch(match[v]))//如果可以匹配
            {
                match[v]=u;//设定匹配
                return 1;
            }
        }
    }
    return 0;
}
int main() {
    while(~scanf("%d%d",&n,&m)) {
        int res=0;
        memset(head,-1,sizeof(head));
        memset(match,0,sizeof(match));
        cnt=0;
        for(int i=1; i<=n; i++) {
            int s;
            scanf("%d",&s);
            while(s--) {
                int x;
                scanf("%d",&x);
                Add(i,x+n);
                //Add(x+n,i);这里不用建双边，因为确定下来匹配关系后可以根据匹配反推
            }
        }
        for(int i=1; i<=n; i++) {
            memset(vis,0,sizeof(vis));
            if(maxmatch(i))res++;
        }
        printf("%d\n",res);
    }
    return 0;
}

POJ1325

题目大意：给出两条机器A，B，A有n种工作模式（0~ n-1），B有m种(0~ m-1)，一开始都在工作模式0下工作，现在给定k个作业，给出每个作业三元组约束 $(i, x, y)$ ，表示可以在A上以x处理或者在B上以y处理，完成工作需要重启以修改机器工作模式，需要安排作业的顺序并分配适当机器使重启次数最少，输出最少的次数

思路：一开始在工作模式0工作，因此可以在工作公式0工作的可忽略，求最少的重启次数，等价于求二分图的最小点覆盖数，等价于求最大匹配，跑匈牙利算法即可

代码

#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=4e4+10;
int n,m,cnt,k,head[500],match[500];
struct node {
    int next,to;
} e[maxn<<1];
void Add(int from,int to) {
    e[++cnt].to=to;
    e[cnt].next=head[from];
    head[from]=cnt;
}
bool vis[500];
bool maxmatch(int u) {//传入左集合节点
    for(int i=head[u]; ~i; i=e[i].next) {//BFS
        int v=e[i].to;
        if(!vis[v]) {//如果没访问过
            vis[v]=1;
            if(!match[v]||maxmatch(match[v])) { //如果可以匹配
                match[v]=u;//设定匹配
                return 1;
            }
        }
    }
    return 0;
}
int main() {
    while(~scanf("%d",&n)&&n) {
        scanf("%d%d",&m,&k);
        int res=0;
        memset(head,-1,sizeof(head));
        memset(match,0,sizeof(match));
        cnt=0;
        while(k--) {
            int i,x,y;
            scanf("%d%d%d",&i,&x,&y);
            if(x==0||y==0)continue;//跳过工作模式0
            Add(x,y+n);
        }
        for(int i=0; i<n; i++) {
            memset(vis,0,sizeof(vis));
            if(maxmatch(i))res++;
        }
        printf("%d\n",res);
    }
    return 0;
}

LuoguP1263

题目大意：略

思路：如果没有墙，把每一行看做左集合，列为右集合，对于空地将所在行与列连边，匈牙利一遍即可，但是墙将行列割裂开来，因此需要将割裂产生的连通块视做单独的个体，也就是修改遍历范围，具体见代码

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=2e4+10;
int m,n,cnt,maze[250][250],match[maxn],head[maxn],res,acch,accz;
int col[maxn],parth[250][250],partz[250][250];
bool vis[maxn];
struct node {
    int next,to;
} e[maxn<<1];
void Add(int from,int to) {//链式前向星
    e[++cnt].next=head[from];
    e[cnt].to=to;
    head[from]=cnt;
}
bool maxmatch(int u) {//最大匹配
    for(int i=head[u]; ~i; i=e[i].next) {
        int v=e[i].to;
        if(!vis[v]) {
            vis[v]=1;
            if(!match[v]||maxmatch(match[v])) {
                match[v]=u;
                return 1;
            }
        }
    }
    return 0;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >>n>>m;
    memset(head,-1,sizeof(head));
    memset(col,-1,sizeof(col));
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            cin >>maze[i][j];
    for(int i=1; i<=n; i++)maze[i][0]=2;//处理边界值
    for(int i=1; i<=m; i++)maze[0][i]=2;//同上
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            if(maze[i][j]<2) {//如果不是墙
                if(maze[i][j-1]>1)parth[i][j]=++acch;//前一个点是墙，产生新的连通块
                else parth[i][j]=parth[i][j-1];//不是墙，合并连通块
            }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            if(maze[i][j]<2) {
                if(maze[i-1][j]>1)partz[i][j]=++accz;//前一个点是墙，产生新的连通块
                else partz[i][j]=partz[i-1][j];//不是墙，合并连通块
            }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            if(maze[i][j]==0)Add(parth[i][j],partz[i][j]);//如果是空地，左右建边
    for(int i=1; i<=acch; i++) {//遍历每个列连通块
        for(int j=1; j<=accz; j++)vis[j]=0;
        res+=maxmatch(i);//统计匹配量
    }
    cout <<res<<endl;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)//match数组记录了所有匹配边
            if(maze[i][j]==0&&parth[i][j]==match[partz[i][j]])cout <<i<<" "<<j<<endl;
            //空地，且行对应列？
    return 0;
}

2019icpc南京J

题目大意：略

思路：KM模板题，但是需要用到真正的 $O(n^3)$ 模板

代码

#include <bits/stdc++.h>
#define int long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=512;
int pre[maxn],match[maxn],delta[maxn],graph[maxn][maxn],n,res,l[maxn],r[maxn];
int a[maxn],p[maxn],b[maxn],c[maxn];
bool visl[maxn],visr[maxn];
void maxmatch(int u) {
    int x,y=0,d,id=0;
    memset(pre,0,sizeof(pre));//pre用来记录上一条边
    for(int i=1; i<=n; i++)delta[i]=inf;//初始化右点集
    match[y]=u;//初始化匹配关系
    while(1) {
        x=match[y];
        d=inf;//初始化
        visr[y]=1;//访问
        for(int i=1; i<=n; i++) {
            if(visr[i])continue;
            if(delta[i]>l[x]+r[i]-graph[x][i]) {//能否加一条边x-i
                delta[i]=l[x]+r[i]-graph[x][i];
                pre[i]=y;//连接一条未匹配边
            }
            if(delta[i]<d) {//找到一条修改值最少的点
                d=delta[i];//记录数值
                id=i;//记录编号
            }
        }
        for(int i=0; i<=n; i++)
            if(visr[i])l[match[i]]-=d,r[i]+=d;//尝试修改
            else delta[i]-=d;//该边不是最短边，减去后可能成为最短边
        y=id;
        if(match[y]==-1)break;//无法继续匹配
    }
    while(y) {//构造匹配
        match[y]=match[pre[y]];
        y=pre[y];
    }
}
int KM() {
    memset(match,-1,sizeof(match));//清空匹配
    memset(l,0,sizeof(l));
    memset(r,0,sizeof(r));
    for(int i=1; i<=n; i++) {
        memset(visr,0,sizeof(visr));
        maxmatch(i);//BFS左点集
    }
    for(int i=1; i<=n; i++)
        if(match[i]!=-1)res+=graph[match[i]][i];
    return res;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >>n;
    for(int i=1; i<=n; i++)cin >>a[i];
    for(int i=1; i<=n; i++)cin >>p[i];
    for(int i=1; i<=n; i++)cin >>b[i];
    for(int i=1; i<=n; i++)cin >>c[i];
    //录入数据
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            for(int k=1; k<=n; k++)
                if(b[i]+c[j]>a[k])graph[i][j]+=p[k];//如果可以打败，建边
    cout <<KM();
    return 0;
}
/*
4
1 2 3 4
1 1 1 1
0 0 1 1
0 1 1 2
*/

LuoguP6577

题目大意：略

思路：KM模板题

代码

#include <bits/stdc++.h>
#define int long long
#define inf 1e18//这里无穷大0x3f3f3f3f小了
using namespace std;
const int maxn=512;
int pre[maxn],match[maxn],delta[maxn],graph[maxn][maxn],n,m,res,l[maxn],r[maxn];
int a[maxn],p[maxn],b[maxn],c[maxn];
bool visl[maxn],visr[maxn];
void maxmatch(int u) {
    int x,y=0,d,id=0;
    memset(pre,0,sizeof(pre));//pre用来记录上一条边
    for(int i=1; i<=n; i++)delta[i]=inf;//初始化右点集
    match[y]=u;//初始化匹配关系
    while(1) {
        x=match[y];
        d=inf;//初始化
        visr[y]=1;//访问
        for(int i=1; i<=n; i++) {
            if(visr[i])continue;
            if(delta[i]>l[x]+r[i]-graph[x][i]) {//能否加一条边x-i
                delta[i]=l[x]+r[i]-graph[x][i];
                pre[i]=y;//连接一条未匹配边
            }
            if(delta[i]<d) {//找到一条修改值最少的点
                d=delta[i];//记录数值
                id=i;//记录编号
            }
        }
        for(int i=0; i<=n; i++)
            if(visr[i])l[match[i]]-=d,r[i]+=d;//尝试修改
            else delta[i]-=d;//该边不是最短边，减去后可能成为最短边
        y=id;
        if(match[y]==-1)break;//无法继续匹配
    }
    while(y) {//构造匹配
        match[y]=match[pre[y]];
        y=pre[y];
    }
}
int KM() {
    memset(match,-1,sizeof(match));//清空匹配
    memset(l,0,sizeof(l));
    memset(r,0,sizeof(r));
    for(int i=1; i<=n; i++) {
        memset(visr,0,sizeof(visr));
        maxmatch(i);//BFS左点集
    }
    for(int i=1; i<=n; i++)
        if(match[i]!=-1)res+=graph[match[i]][i];
    return res;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >>n>>m;
    for(int i=1; i<=n; i++)//注意初始化
        for(int j=1; j<=n; j++)
            graph[i][j]=-inf;
    while(m--) {
        int x,y,w;
        cin >>x>>y>>w;
        graph[x][y]=w;
    }
    cout <<KM()<<endl;
    for(int i=1; i<=n; i++)
        cout <<match[i]<<" ";
    return 0;
}

LuoguP4014

题目大意：略

思路：最大总收益直接用KM求解，最小收益需要对边权取反然后跑KM，跑完之后对结果取反即可

代码

#include <bits/stdc++.h>
#define int long long
#define inf 1e18
using namespace std;
const int maxn=512;
int pre[maxn],match[maxn],delta[maxn],graph[maxn][maxn],n,m,res,l[maxn],r[maxn];
bool visl[maxn],visr[maxn];
void maxmatch(int u) {
    int x,y=0,d,id=0;
    memset(pre,0,sizeof(pre));//pre用来记录上一条边
    for(int i=1; i<=n; i++)delta[i]=inf;//初始化右点集
    match[y]=u;//初始化匹配关系
    while(1) {
        x=match[y];
        d=inf;//初始化
        visr[y]=1;//访问
        for(int i=1; i<=n; i++) {
            if(visr[i])continue;
            if(delta[i]>l[x]+r[i]-graph[x][i]) {//能否加一条边x-i
                delta[i]=l[x]+r[i]-graph[x][i];
                pre[i]=y;//连接一条未匹配边
            }
            if(delta[i]<d) {//找到一条修改值最少的点
                d=delta[i];//记录数值
                id=i;//记录编号
            }
        }
        for(int i=0; i<=n; i++)
            if(visr[i])l[match[i]]-=d,r[i]+=d;//尝试修改
            else delta[i]-=d;//该边不是最短边，减去后可能成为最短边
        y=id;
        if(match[y]==-1)break;//无法继续匹配
    }
    while(y) {//构造匹配
        match[y]=match[pre[y]];
        y=pre[y];
    }
}
int KM() {
    memset(match,-1,sizeof(match));//清空匹配
    memset(l,0,sizeof(l));
    memset(r,0,sizeof(r));
    for(int i=1; i<=n; i++) {
        memset(visr,0,sizeof(visr));
        maxmatch(i);//BFS左点集
    }
    for(int i=1; i<=n; i++)
        if(match[i]!=-1)res+=graph[match[i]][i];
    return res;
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >>n;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            cin >>graph[i][j];
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            graph[i][j]*=-1;
    cout <<-KM()<<endl;
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            graph[i][j]*=-1;
    res=0;
    cout <<KM()<<endl;
    return 0;
}

LuoguP1971

题目大意：略

思路：利用相对位移的思想，将棋子的移动视为空格的移动，那么先手将空格移动到白子，这与黑子的性质类似，因此将空格看做黑，这样整个迷宫就可以转换成黑白两子间两两匹配的问题，黑白染色，建二分图，根据二分图博弈的思路，分别判断当前移动的点位置在移动前是否为最大匹配必须点，如果是，当前手必赢，否则必输

判断当前点位置是否为最大匹配必须点，可以将点从图中删掉并删掉原先的匹配关系，查看原匹配关系的另一个点是否能组成另一个最大匹配，如果能，代表当前点并不是必须点，则当前手必输（按照最优策略的话），因为当前手下一步必然入最大匹配，记录每一步的当前手是否必输必赢，判断一开始的先手是否错误，需要判断第k轮是否先手必胜而下完后后手必胜，即两个状态都为1，代表这一步先手错了，记录即可

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=5e3+10;
int n,m,k,sx,sy,cnt,head[maxn],match[maxn];
vector<int>res;
char maze[50][50];
bool color[50][50],vis[maxn/2],block[maxn/2],win[maxn/2];
struct node {
    int next,to;
} e[maxn];
void Add(int from,int to) {//链式前向星
    e[++cnt].to=to;
    e[cnt].next=head[from];
    head[from]=cnt;
}
int Hash(int i,int j) {//离散化坐标
    return (i-1)*m+j;
}
bool maxmatch(int u) {
    for(int i=head[u]; ~i; i=e[i].next) {
        int v=e[i].to;
        if(block[v])continue;//这个点已经被去掉了
        if(!vis[v]) {
            vis[v]=1;
            if(!match[v]||maxmatch(match[v])) {
                match[v]=u;
                match[u]=v;
                return 1;
            }
        }
    }
    return 0;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >>n>>m;
    memset(head,-1,sizeof(head));
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++) {
            cin >>maze[i][j];
            if(maze[i][j]=='.')//存起点
                sx=i,sy=j;
            else if(maze[i][j]=='O')//标记白点
                color[i][j]=1;
        }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            if(color[i][j]) {
                if(i+1<=n&&!color[i+1][j]) {//建边
                    Add(Hash(i,j),Hash(i+1,j));
                    Add(Hash(i+1,j),Hash(i,j));
                }
                if(j+1<=m&&!color[i][j+1]) {
                    Add(Hash(i,j+1),Hash(i,j));
                    Add(Hash(i,j),Hash(i,j+1));
                }
                if(i>1&&!color[i-1][j]) {//建边
                    Add(Hash(i,j),Hash(i-1,j));
                    Add(Hash(i-1,j),Hash(i,j));
                }
                if(j>1&&!color[i][j-1]) {//建边
                    Add(Hash(i,j),Hash(i,j-1));
                    Add(Hash(i,j-1),Hash(i,j));
                }
            }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            if(color[i][j]&&!match[Hash(i,j)]) {//以白点为基础建边
                memset(vis,0,sizeof(vis));
                maxmatch(Hash(i,j));//匹配
            }
    cin >>k;
    for(int i=1; i<=2*k; i++) {
        int id=Hash(sx,sy);
        block[id]=1;//代表这一个已经访问过了，不能作为匹配
        if(match[id]==0)//这一点为非必须/非匹配点，下一步必然在匹配点，下一个人必赢
            win[i]=0;
        else {
            int t=match[id];//t不会与id匹配，因为已经在block上标记了
            match[id]=match[t]=0;
            memset(vis,0,sizeof(vis));
            if(maxmatch(t))win[i]=0;
            else win[i]=1;
            //尝试去掉id开始匹配，如果仍然存在最大匹配，则id为非必须点
            //非必须点为起点，下一个人必在匹配点，下一个人必赢
        }
        cin >>sx>>sy;//录入下一次操作
    }
    for(int i=1; i<=k; i++)
        if(win[2*i-1]&&win[2*i])//如果A本来可以赢，但是下完之后B赢了，代表A下错了
            res.push_back(i);
    int len=res.size();
    cout <<len<<endl;
    for(int i=0; i<len; i++)
        cout <<res[i]<<endl;
    return 0;
}

LuoguP4055

题目大意：略

思路：首先声明一下：

该题数据有问题！该题数据有问题！该题数据有问题！

数据忽略了类似下面两种的数据

3 3  3 3
.##  .##
.##  .##
..#  #..

因此，洛谷上的部分题解可能思路是对的，但是代码从逻辑上是错的，下面给出的代码我自己也不能保证就是对的，因为没有更全面的数据

下面是思路

根据题意，相邻的可行格显然可以连边，那么采用黑白染色的方法将整个可行域分成黑白两部分，这样就可以构造一个二分图了，题目也就转变成了二分图博弈，但是本题的先手是先选点，不是从起点出发
为了先手必胜，那么先手就需要使后手走之后使当前点为最大匹配的起点，这样就和二分图博弈的模型相符合了，那么先手需要找的点就是与最大匹配相连，但可以不属于最大匹配的点，如果整个图是完全匹配，显然是没有这样的点的

最大匹配可能有多个，如果先手走了某个最大匹配的必须点，显然后手就从博弈模型中的“起点”开始走了，先手会输，所以，先手需要走所有最大匹配都非必须的点

为了找所有最大匹配的必须点，可以从一个非必须点开始搜索，假设其颜色为黑，如果经过一个白点搜索还能搜到黑，那么另一个黑点必然也是非必须点，因为这两个点等价，那么它们与公共点组成的边就可以替换原图中最大匹配的一条边，可以画图尝试

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,match[maxn],head[maxn],cnt,ans,res,color[maxn];
int point[1212][1212];
char maze[1212][1212];
bool vis[maxn],une[maxn];
struct node {
    int next,to;
} e[maxn];
void Add(int from,int to) {
    e[++cnt].to=to;
    e[cnt].next=head[from];
    head[from]=cnt;
}
bool maxmatch(int u) {
    for(int i=head[u]; ~i; i=e[i].next) {
        int v=e[i].to;
        if(!vis[v]) {
            vis[v]=1;
            if(match[v]==-1||maxmatch(match[v])) {
                match[v]=u;
                return 1;
            }
        }
    }
    return 0;
}
void DFS(int u) {
    if(une[u])return ;
    une[u]=1;
    for(int i=head[u]; ~i; i=e[i].next) {
        int v=e[i].to;
        if(match[v]!=-1)
            DFS(match[v]);
    }
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >>n>>m;
    memset(match,-1,sizeof(match));
    memset(head,-1,sizeof(head));
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            cin >>maze[i][j];
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            if(maze[i][j]=='.') {
                point[i][j]=++ans;//离散化
                if((i+j)%2==0)color[ans]=1;//染色，一个小技巧
             	//只染色了偶数和格，可以保证奇数和格必为0
            }
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            if(maze[i][j]=='.') {//建图
                if(point[i+1][j]) {//利用已经离散化的坐标来代替
                    Add(point[i][j],point[i+1][j]);
                    Add(point[i+1][j],point[i][j]);
                }
                if(point[i][j+1]) {
                    Add(point[i][j],point[i][j+1]);
                    Add(point[i][j+1],point[i][j]);
                }
            }
    for(int i=1; i<=ans; i++)//构造最大匹配
        if(color[i]) {//以黑点为基准
            memset(vis,0,sizeof(vis));
            if(match[i]==-1)
                res+=maxmatch(i);
        }
    if(cnt/2==res||(ans/2==res&&cnt/2+1==ans)) {//特判是否无解
        cout <<"LOSE"<<endl;
        return 0;
    }
    cout <<"WIN"<<endl;
    for(int i=1; i<=ans; i++)//反标记，代表已经在最大匹配上
        if(match[i]!=-1)match[match[i]]=i;
    for(int i=1; i<=ans; i++)if(match[i]==-1)DFS(i);
    //如果是非必须点，找另一个非必须点
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            if(une[point[i][j]])//根据离散化坐标判断是否为非必须点
                cout <<i<<" "<<j<<endl;
    return 0;
}
/*
3 3
.##
.##
..#
*/

总结

二分图最基础的知识点就是最大匹配和染色，其余的知识点都是在这两点上延伸拓展的，需要深刻理解，由LuoguP1285可以看到，二分图可以将整个图变成一个个具有双重性质的连通块，而如果将这些连通块套入背包模型，便可以用DP的思路来解决问题，这是非常巧妙的
二分图，准确来说，是一种思想，一种思维，如何将问题转换成二分图，如何套用二分图模型解决问题，这是需要掌握的

KM算法是最大匹配的拓展，确切的来说，它利用了顶标与边权来进行取值约束，通过不断的修改顶标间接的修改所取的边与匹配关系，最后获得最大权匹配

二分图的问题大多数可以用网络流的其他算法来解决，但是由于二分图的特殊性，二分图本身的相关算法还是更加适配自身的问题