[数据结构与算法]【冬令营 Winter Camp】搜索专题

A - 棋盘问题

在一个给定形状的棋盘（形状可能是不规则的）上面摆放棋子，棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列，请编程求解对于给定形状和大小的棋盘，摆放k个棋子的所有可行的摆放方案C。

Sample Input

2 1
#.
.#
4 4
...#
..#.
.#..
#...
-1 -1

2
1

思路：深度优先遍历，一行一行判断能否放棋子，每一行需要判断每一列能否放能放，能放/不能放也都递归到下一行（这样能包含所有放棋子的情况），注意回溯。

Java

import java.util.Scanner;

public class Main {
    static int n, k, cnt;
    static char[][] array;
    static boolean[] used;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            n = sc.nextInt();
            k = sc.nextInt();
            if (n == -1 && k == -1)
                break;
            cnt = 0;
            array = new char[n][n];
            used = new boolean[n];
            sc.nextLine();
            for (int i = 0; i < n; i++) {
                array[i] = sc.nextLine().toCharArray();
            }
            dfs(0, 0);
            System.out.println(cnt);
        }
    }
    public static void dfs(int i, int sum) {
        if (i == n) {
            if (sum == k) {
                cnt++;
            }
            return;
        }
        for (int j = 0; j < n; j++) {
            if (array[i][j] == '.')
                continue;
            if (!used[j]) {
                used[j] = true;
                dfs(i+1, sum+1);
                used[j] = false;
            }
        }
		dfs(i+1, sum);
    }
}

C++

#include<iostream>
#include<string.h>
using namespace std;

int n, k, cnt;
char a[10][10];
bool flag[10];

void dfs(int x, int sum) {
    if (x == n) {
        if (sum == k)
            cnt++;
        return;
    }
    // 遍历一行的每一列，判断能否放棋子
    for (int i = 0; i < n; i++) {
        if (a[x][i] == '.' || flag[i])  // 如果当前x,i位置为.或者是所在行列已经被占用则跳过
            continue;
        flag[i] = true;  // 修改标记数组
        dfs(x+1, sum+1);  // 放一枚棋子递归下一行
        flag[i] = false;  // 回溯
    }
    // 这一行不放棋子，跳过（模拟所有）
    dfs(x+1, sum);
}
int main() {
    while (1) {
        cin >> n >> k;

        if (n == -1 && k == -1)
            break;
        
        // 每次测试都需要修改全局变量的初始值
        memset(flag, false, sizeof(flag)); 
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                cin >> a[i][j];
            }
        }
        cnt = 0;
        dfs(0, 0);
        printf("%d\n", cnt);
    }
    return 0;
}

B - Perket

你有 N 种配料，每种配料有酸度 S 和苦度 B 。用这些配料做成Perket时，总的酸度为所有配料酸度的乘积，总的苦度是所有配料苦度的和。你至少需要添加一种配料。

为了使口感适中，总的酸度和苦度之差的绝对值应该尽可能小，求这个最小值。

4
1 7
2 6
3 8
4 9

1

Java

import java.util.Scanner;

public class Main {
    static int n, k, cnt;
    static int[][] array;
    static boolean[] used;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        array = new int[n][2];
        cnt = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
            array[i][0] = sc.nextInt();
            array[i][1] = sc.nextInt();
        }
        dfs(0, 1, 0, 0);
        System.out.println(cnt);
    }
    public static void dfs(int i, int a, int b, int k) {
        if (i == n) {
            if (k > 0)
                cnt = Math.min(cnt, Math.abs(a - b));
            return;
        }
        dfs(i+1, a*array[i][0], b + array[i][1], k+1);
        dfs(i+1, a, b, k);
    }
}

C++

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 1E5 + 7;
ll current_exception = 1e9+10;
ll arr[10][2];
ll n, k, cnt = 1e9+1;

void dfs(ll i, ll a, ll b) {
    if (i == n) {
        if (k > 0)
            cnt = min(cnt, abs(a - b));
        return;
    }
    k++;
    dfs (i + 1, a * arr[i][0], b + arr[i][1]);
    k--;
    dfs(i + 1, a, b);
}
int main()
{
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> arr[i][0] >> arr[i][1];
    }
    dfs(0, 1, 0);
    cout << cnt;
}

思路：n<=10,数据较小，暴力求解，每一个都试试加入和不加入两种情况，取最小值，来源：大佬博客

#include<iostream>
#include<cmath>
#include<string.h>
#include<algorithm>
#include<map>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const int maxn=200100;
const int INF=pow(2,31)-1;
const int maxm=5e4+5;
const int mod=1000000007;
ll n;
ll s[maxn],b[maxn];
ll ans,cnt;
ll mi=1e9+10;
/*bool judge(ll x){
    for(int i=1;i<=n;i++){

    }
}*/
void dfs(ll step,ll k){
    if(step==n+1){
        if(k>=1)mi=min(mi,abs(ans-cnt));
        return ;
    }
    ans*=s[step];
    cnt+=b[step];
    dfs(step+1,k+1);
    cnt-=b[step];
    ans/=s[step];
    dfs(step+1,k);
    return ;
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>s[i]>>b[i];
    }
    ans=1;
    dfs(1,0);
    cout<<mi<<endl;
    return 0;
}

C - 全排列

给定一个由不同的小写字母组成的字符串，输出这个字符串的所有全排列。我们假设对于小写字母有’a’< ‘b’< …<‘y’<‘z’，而且给定的字符串中的字母已经按照从小到大的顺序排列。

输入格式

输入只有一行，是一个由不同的小写字母组成的字符串，已知字符串的长度在1到6之间。

输出格式

输出这个字符串的所有排列方式，每行一个排列。要求字母序比较小的排列在前面。

abc

abc
acb
bac
bca
cab
cba

Java

参考：洛谷 P1706 全排列问题（Java版）

import java.util.Scanner;

public class Main {
    static int n, k, cnt;
    static int[][] array;
    static char[] arr;
    static boolean[] used;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        arr = sc.nextLine().toCharArray();
        used = new boolean[arr.length];
        Arrays.sort(arr);
        fullSort(new StringBuilder());
    }
    public static void fullSort(StringBuilder res) {
        if (res.length() == arr.length) {
            System.out.println(res.toString());
            return;
        }
        for (int i = 0; i < arr.length; i++) {
            if (!used[i]) {
                used[i] = true;
                res.append(arr[i]);
                fullSort(res);
                res.deleteCharAt(res.length()-1);
                used[i] = false;
            }
        }
    }
}

C++

#include<iostream>
#include<cmath>
#include<string.h>  // strlen()
#include<algorithm>  // 排序操作
#include<map>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const int maxn=200100;
const int INF=pow(2,31)-1;
const int maxm=5e4+5;
const int mod=1000000007;
char str[maxn],st[maxn];  // 字符数组
ll cnt;
ll used[maxn];
ll n;
void dfs(ll step){
    // 输出结果
    if(step==n+1){
        for(int i=1;i<=cnt;i++){
            cout<<st[i];
        }
        cout<<endl;
        return ;
    }
    for(int i=1;i<=n;i++){
        if(!used[i]){
            used[i]=1;
            st[++cnt]=str[i];
            dfs(step+1);
            used[i]=0;
            cnt--;
        }
    }
    return ;
}
int main(){
    cin>>(str+1);
    n=strlen(str+1);
    sort(str+1,str+1+n);
    dfs(1);
    return 0;
}

D - 自然数拆分

对于任意大于 1 的自然数 n，总是可以拆分成若干个小于 n 的自然数之和。

现请你编写程序求出 n 的所有拆分。

5

5=1+1+1+1+1
5=1+1+1+2
5=1+1+3
5=1+2+2
5=1+4
5=2+3

思路：通过不断进行分层，来进行求解，每一层的初始位置从上一次分解的位置开始，可以保证所有解都可以求出，另外排除5=5，这种情况

Java

import java.util.Scanner;

public class Main {
    static int n, k, cnt;
    static int[] arr;
    static boolean[] used;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        arr = new int[n];
        k = -1;
        fullSort(0, 1);
    }
    public static void fullSort(int sum, int x) {
        if (sum > n)
            return;
        if (sum == n) {
            System.out.print(n+"=");
            for (int i = 0; i < k; i++) {
                System.out.print(arr[i] + "+");
            }
            System.out.println(arr[k]);
            return;
        }
        for (int i = x; i < n; i++) {
            k++;
            arr[k] = i;
            fullSort(sum+i, i);
            k--;
        }
    }
}

C++

#include<iostream>
#include<cmath>
#include<string.h>
#include<algorithm>
#include<map>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const int maxn=200100;
const int INF=pow(2,31)-1;
const int maxm=5e4+5;
const int mod=1000000007;
ll n;
ll cnt;
ll a[maxn];
ll sum;
void dfs(ll x){
    if(sum==n){
        printf("%lld=",n);
        for(int i=1;i<cnt;i++){
            printf("%lld+",a[i]);
        }
        printf("%lld\n",a[cnt]);
        return ;
    }
    if(sum>n)return ;
    for(int i=x;i<n;i++){
        sum+=i;
        cnt++;
        a[cnt]=i;
        dfs(i);
        cnt--;
        sum-=i;
    }
    return ;
}
int main(){
    cin>>n;
    dfs(1);
    return 0;
}

E - Prime Ring Problem

输入正整数n，把整数1,2…,.排成一个环，使得相邻两个整数之和均为素数。输出时，从整数1开始逆时针排列。同一个环恰好输出一次。n≤16，保证一定有解。

多组数据，读入到EOF结束。

第i组数据输出前加上一行Case i :

相邻两组输出中间加上一个空行。

6
8

Case 1:
1 4 3 2 5 6
1 6 5 2 3 4

Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2

行末无空格
最后一个Case输出后不换行

Java

思路：规定第一个数为1，其余数按照全排列的方法进行即可，判断条件加上相邻两个数为素数的条件，最后输出格式需要注意一下

超时！

package WinterCamp.StringTest;

import java.util.Scanner;

public class C {
    static int n, k;
    static int[] arr;
    static boolean[] used;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int flag = 0;
        while (sc.hasNext()) {
            n = sc.nextInt();
            arr = new int[n+1];
            used = new boolean[n+1];
            arr[1] = 1;
            k = 1;
            if (flag++ > 0)
                System.out.println();
            System.out.println("Case "+flag+":");
            fullSort(2);
        }
    }
    public static void fullSort(int x) {
        if (x == n+1) {
            if (judge(arr[1]+arr[k])) {
                for (int i = 1; i < k; i++)
                    System.out.print(arr[i]+" ");
                System.out.println(arr[k]);
            }
            return;
        }
        for (int i = 2; i <= n; i++) {
            if (used[i])
                continue;
            if (judge(arr[k]+i)) {
                used[i] = true;
                k++;
                arr[k] = i;
                fullSort(x + 1);
                used[i] = false;
                k--;
            }
        }
    }
    public static boolean judge(int x) {
        if (x == 1)
            return false;
        for (int i = 2; i * i <= x; i++) {
            if (x % i == 0)
                return false;
        }
        return true;
    }
}

C++

#include<iostream>
#include<cmath>
#include<string.h>
#include<algorithm>
#include<map>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const int maxn=200100;
const int INF=pow(2,31)-1;
const int maxm=5e4+5;
const int mod=1000000007;
ll n;
ll a[maxn];
ll cnt;
ll used[maxn];
bool judge(ll x){
    if(x==1)return false;
    for(int i=2;i*i<=x;i++){
        if(x%i==0)return false;
    }
    return true;
}
void dfs(ll x){
    if(x==n+1){
        if(judge(a[cnt]+a[1])){
            for(int i=1;i<cnt;i++){
                printf("%lld ",a[i]);
            }
            printf("%lld\n",a[cnt]);
        }
        return ;
    }
    for(int i=2;i<=n;i++){
        if(used[i])continue;
        if(judge(a[cnt]+i)){
            used[i]=1;
            cnt++;
            a[cnt]=i;
            dfs(x+1);
            used[i]=0;
            cnt--;
        }
    }
    return ;
}
int main(){
    ll f1=0;
    while(cin>>n){
        if(f1)printf("\n");
        f1++;//对输出格式的控制
        printf("Case %lld:\n",f1);
        a[1]=1;
        cnt=1;
        dfs(2);

    }
    return 0;
}

F - Red and Black

有一个长方形的房间，覆盖了正方形的磁砖。每块磁砖的颜色，要么是红色，要么是黑色。一名男子站在一块黑色的磁砖上。他可以从一块磁砖移至相邻四块磁砖中的某一块。但是，他不允许在红色磁砖上移动，他只允许在黑色磁砖上移动。

编写一个程序，使得他允许重复上述的移动，判断他所能到达的黑色磁砖的数量。

6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
11 9
.#.........
.#.#######.
.#.#.....#.
.#.#.###.#.
.#.#..@#.#.
.#.#####.#.
.#.......#.
.#########.
...........
11 6
..#..#..#..
..#..#..#..
..#..#..###
..#..#..#@.
..#..#..#..
..#..#..#..
7 7
..#.#..
..#.#..
###.###
...@...
###.###
..#.#..
..#.#..
0 0

45
59
6
13

Java

import java.util.Scanner;

public class Main {
    static int n, k, cnt, a, b, sx, sy;
    static char[][] arr;
    static boolean[][] used;
    static int[] orient = {0, 1, 0, -1, 0};
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (true) {
            a = sc.nextInt();
            b = sc.nextInt();
            if (a == 0 && b == 0)
                break;
            cnt = 1;
            arr = new char[b+1][a+1];
            used = new boolean[b+1][a+1];
            for (int i = 1; i <= b; i++) {
                String s = sc.next();
                s = " " + s;
                if (s.contains("@")) {
                    sx = i;
                    sy = s.indexOf("@");
                }
                arr[i] = s.toCharArray();
            }
            dfs(sx, sy);
            System.out.println(cnt);
        }
    }
    public static void dfs(int x, int y) {
        used[x][y] = true;
        for (int i = 0; i < 4; i++) {
            int xx = x + orient[i], yy = y + orient[i+1];
            if (xx < 1 || yy < 1 || xx > b || yy > a || used[xx][yy] || arr[xx][yy] == '#')
                continue;
            if (arr[xx][yy] == '.') {
                cnt++;
                dfs(xx, yy);
            }
        }
    }
}

C++

#include<iostream>
using namespace std;
#include<string.h>
typedef long long int ll;
const int maxn = 200100;

ll a, b, sx, sy, used[100][100], orient[5]={0, 1, 0, -1, 0}, cnt;
char arr[100][100];

void dfs(ll x, ll y) {
    used[x][y] = 1;
    for (int i = 0; i < 4; i++) {
        ll xx = x + orient[i], yy = y + orient[i+1];
        if (xx < 1 || yy < 1 || xx > b || yy > a || used[xx][yy] || arr[xx][yy] == '#')
                continue;
        if (arr[xx][yy] == '.') {
            cnt++;
            dfs(xx, yy);
        }
    }
}
int main() {
    while (1) {
        cin >> a >> b;
        if (!a&&!b)
            break;
        memset(used, 0, sizeof(used));
        cnt = 1;
        for(int i=1;i<=b;i++){
            for(int j=1;j<=a;j++){
                cin >> arr[i][j];
                if(arr[i][j]=='@'){
                    sx=i;
                    sy=j;
                }
            }
        }
        dfs(sx, sy);
        printf("%lld\n", cnt);
    }
}

G - Knight Moves

编写一个程序，计算一个骑士从棋盘上的一个格子到另一个格子所需的最小步数。骑士一步可以移动到的位置由下图给出。

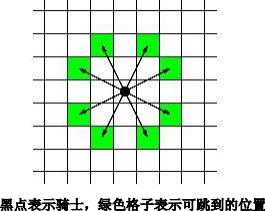
输入格式

第一行给出骑士的数量n。

在接下来的3n行中，每3行描述了一个骑士。其中，
·第一行一个整数L表示棋盘的大小，整个棋盘大小为L×L;
·第二行和第三行分别包含一对整数(z,g)，表示骑士的起始点和终点。假设对于每一个骑士，起始点和终点均合理。

输出格式

对每一个骑士，输出一行一个整数表示需要移动的最小步数。如果起始点和终点相同，则输出0。

3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1

5
28
0

思路：搜索题目，单向bfs搜索超时，所以用双向的，用bfs的原因是求最短路径且数据较大

• 双向bfs：
  单向BFS只从起点一端开始搜索，双向BFS则是从起点和终点两边扩展节点，当节点发生重合时即找到最优解。

实现方法为：维护两个队列，分别保存从起点和终点扩展到的下一层，这样保证了两个队列中的节点处于相同的深度（即：距离起点或者终点深度相同）。则当拓展到时一定发生重合，得到最优解。

Java

有bug的代码！

import java.util.*;

public class C {
    static int k, cnt, a, b;
    static char[][] arr;
    static boolean[][] used;
    static int[] orient = {0, 1, 0, -1, 0};
    static int[] ori = {1, 2, -1, -2, 1, -2, -1, 2, 1};
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        Queue<int[]> p = new LinkedList<>();
        while (n-- > 0) {
            k = sc.nextInt();
            boolean[][] vis = new boolean[k][k];
            p.clear();
            int[] s = new int[3];
            s[0] = sc.nextInt();
            s[1] = sc.nextInt();
            s[2] = 0;
            int ex = sc.nextInt();
            int ey = sc.nextInt();
            p.offer(s);
            vis[s[0]][s[1]] = true;
            int[] cur = new int[3];
            int[] loc;
            while (!p.isEmpty()) {
                loc = p.poll();
                if (loc[0] == ex && loc[1] == ey) {
                    System.out.println(loc[2]);
                    break;
                }
                for (int i = 0; i < 8; i++) {
                    cur[0] = loc[0] + ori[i];
                    cur[1] = loc[1] + ori[i+1];

                    if (judge(cur[0], cur[1]) && !vis[cur[0]][cur[1]]) {
                        cur[2] = loc[2]+1;
                        vis[cur[0]][cur[1]] = true;
                        p.offer(cur);
                    }
                }
            }
        }
    }
    public static boolean judge(int x, int y) {
        if (x < 0 || x >= k || y < 0 || y >= k)
            return false;
        return true;
    }
}

C++

#include<iostream>
#include<cmath>
#include<string.h>
#include<algorithm>
#include<map>
#include<queue>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const int maxn=200100;
const int INF=pow(2,31)-1;
const int maxm=5e4+5;
const int mod=1000000007;
ll t,n;
ll dirx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
ll diry[8] = {-1, -2, -2, -1, 1, 2, 2, 1};
ll dist1[1010][1010],dist2[1010][1010];
struct node{
    ll x;
    ll y;
}st,en;
ll judge(ll x,ll y){
    if(x<0||x>=n||y<0||y>=n){
        return 0;
    }
    return 1;
}
void bfs(){
    queue<node> p,q;
    p.push(st);
    dist1[st.x][st.y]=0;
    q.push(en);
    dist2[en.x][en.y]=0;
    while(!q.empty()&&!p.empty()){
        ll s=p.size();
        node t,tt;
        //cout<<s<<endl;
        while(s--){
            t=p.front();
            p.pop();
            if(judge(t.x,t.y)&&dist2[t.x][t.y]!=-1){
                printf("%lld\n",dist1[t.x][t.y] + dist2[t.x][t.y]);//p走到t,q走到t
                return ;
            }
            for(int i=0;i<8;i++){
                tt.x=t.x+dirx[i];
                tt.y=t.y+diry[i];
                //cout<<tt.x<<" "<<tt.y<<" "<<judge(tt.x,tt.y)<<endl;
                if(judge(tt.x,tt.y)){
                    if(dist2[tt.x][tt.y]!=-1){
                        printf("%lld\n",dist1[t.x][t.y] + dist2[tt.x][tt.y]+1);//p走到t,q走到tt
                        return ;
                    }
                    if(dist1[tt.x][tt.y]==-1){
                       // cout<<tt.x<<" "<<tt.y<<" "<<judge(tt.x,tt.y)<<endl;
                        dist1[tt.x][tt.y]=dist1[t.x][t.y]+1;
                        p.push(tt);
                    }
                }
            }
        }
        //cout<<p.size()<<" "<<q.size()<<endl;
        s=q.size();
        while(s--){
            t=q.front();
            q.pop();
            if(judge(t.x,t.y)&&dist1[t.x][t.y]!=-1){
                    printf("%lld\n",dist1[t.x][t.y] + dist2[t.x][t.y]);//p走到t,q走到t
                    return ;
            }
            for(int i=0;i<8;i++){
                tt.x=t.x+dirx[i];
                tt.y=t.y+diry[i];
                if(judge(tt.x,tt.y)){
                    if(dist1[tt.x][tt.y]!=-1){
                        printf("%lld\n",dist2[t.x][t.y] + dist1[tt.x][tt.y]+1);//p走到tt,q走到t
                        return ;
                    }
                    if(dist2[tt.x][tt.y]==-1){
                        dist2[tt.x][tt.y]=dist2[t.x][t.y]+1;
                        q.push(tt);
                    }
                }
            }
        }
        //cout<<p.size()<<" "<<q.size()<<endl;
    }

}
int main(){
    cin>>t;
    while(t--){
        cin>>n;
        cin>>st.x>>st.y;
        cin>>en.x>>en.y;
        memset(dist1,-1,sizeof(dist1));
        memset(dist2,-1,sizeof(dist2));
        bfs();
    }
    return 0;
}

参考2：

#include<bits/stdc++.h>
using namespace std;
int n;
#define MAXN 305
char a[MAXN][MAXN];
bool vis[MAXN][MAXN];
int dir[8][2]={{-2,1},{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2},{-2,-1}};
struct node
{
    int x;
    int y;
    int step;
}q[100005];
void bfs(int sx,int sy,int ex,int ey)//bfs
{
    int head=1,tail=1;
    memset(vis,0,sizeof(vis));
    vis[sx][sy]=1;
    q[tail].x=sx;
    q[tail].y=sy;
    q[tail].step=0;
    tail++;
    while(head<tail)
    {
        int x=q[head].x;
        int y=q[head].y;
        int step=q[head].step;
        if(x==ex&&y==ey)
        {
            printf("%d\n",step);
            break;
        }
        for(int i=0;i<8;i++)//注意有八个方向
        {
            int nx=x+dir[i][0];
            int ny=y+dir[i][1];
            if(nx>=0&&nx<n&&ny>=0&&ny<n&&vis[nx][ny]==0)
            {
                vis[nx][ny]=1;
                q[tail].x=nx;
                q[tail].y=ny;
                q[tail].step=step+1;
                tail++;
            }
        }
        head++;
    }
}
int main()
{
    int t;
    int sx,sy,ex,ey;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        scanf("%d%d%d%d",&sx,&sy,&ex,&ey);
        bfs(sx,sy,ex,ey);
    }
    return 0;
}

参考3：一个简单的马走日问题，其中每一个点到达的8个地点都需要记录步数。

#include<bits/stdc++.h>
using namespace std;
int n, cnt;
#define MAXN 305
char a[MAXN][MAXN];
bool vis[MAXN][MAXN];
int dir[9] = {1, 2, -1, -2, 1, -2, -1, 2, 1};
struct node
{
    int x;
    int y;
    int step;
};
void bfs(int sx,int sy,int ex,int ey)//bfs
{
    memset(vis,0,sizeof(vis));
    node now, next;
    vis[sx][sy]=1;
    now.x = sx;
    now.y = sy;
    now.step = 0;
    queue<node> q;
    q.push(now);
    while(!q.empty())
    {
        now = q.front();
        q.pop();
       
        if(now.x == ex && now.y == ey)
        {
            printf("%d\n", now.step);
            break;
        }
        for(int i = 0; i<8; i++)//注意有八个方向
        {
            next.x = now.x + dir[i];
            next.y = now.y + dir[i+1];
            if(next.x >=0 && next.x < n && next.y >= 0 && next.y < n && vis[next.x][next.y]==0)
            {
                vis[next.x][next.y]=1;
                next.step = now.step + 1;
                q.push(next);
            }
        }
    }
}
int main()
{
    int t;
    int sx,sy,ex,ey;
    scanf("%d",&t);
    while(t--)
    {
        cnt = 0;
        scanf("%d", &n);
        scanf("%d%d%d%d", &sx, &sy, &ex, &ey);
        bfs(sx, sy, ex, ey);
    }
    return 0;
}

H - Oil Deposits

某公司负责探测地下油层，每次处理一个大的矩形区域。先创建一个网格，将土地划分为许多方形块，然后用传感设备分别探测每个地块，以确定该地块是否含有石油。一块含有石油的土地叫做pocket。如果两个pocket边相邻或对角相邻，则它们属于同一油层的一部分。你的工作是确定在一个网格有多少不同的油层。

1 1
*
3 5
*@*@*
**@**
*@*@*
1 8
@@****@*
5 5 
****@
*@@*@
*@**@
@@@*@
@@**@
0 0

0
1
2
2

C++

思路：本题目属于连通图题目，从一个点出发将能遍历的全部遍历一遍，有多少个出发点就有多少个联通块

#include<iostream>
using namespace std;
#include<string.h>
typedef long long int ll;
ll ori[10] = {0, 1, 0, -1, 0, 1, 1, -1, -1, 1};
ll n, m;
char a[110][110];
bool vis[110][110];
ll cnt;

void dfs(ll x, ll y) {
    vis[x][y] = 1;
    for (int i = 0; i < 9; i++) {
        ll xx = x + ori[i];
        ll yy = y + ori[i+1];
        if(xx<1 || xx>n || yy<1 || yy>m)
            continue;
        if (a[xx][yy] == '@' && !vis[xx][yy])
            dfs(xx, yy);
    }
}
int main() {
    while (1) {
        cin >> n >> m;
        memset(vis, 0, sizeof(vis));
        cnt = 0;
        if (n == 0 && m == 0)
            break;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                cin >> a[i][j];
            }
        }
         for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                if(a[i][j]=='@' && !vis[i][j]) {
                    dfs(i,j);
                    cnt++;
                }
            }
        }
        printf("%lld\n",cnt);
    }
}

I - Lake Counting

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.

3

Java

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int cnt, m, n;
    static int[] ori = {0, 1, 0, -1, 0, 1, 1, -1, -1, 1};
    static char[][] arr;
    static boolean[][] vis;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
            m = sc.nextInt();
            n = sc.nextInt();
            int cnt = 0;

            arr = new char[m][n];
            vis = new boolean[m][n];
            for (int i = 0; i < m; i++) {
                arr[i] = sc.next().toCharArray();
            }
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    if (arr[i][j] == 'W' && !vis[i][j]) {
                        dfs(i, j);
                        cnt++;
                    }
                }
            }
            System.out.println(cnt);
    }
    public static void dfs(int x, int y) {
        vis[x][y] = true;
        for (int i = 0; i < 9; i++) {
            int xx = x + ori[i];
            int yy = y + ori[i+1];
            if (xx < 0 || xx >= m || yy < 0 || yy >= n)
                continue;
            if (arr[xx][yy] == 'W' && !vis[xx][yy])
                dfs(xx, yy);
        }
    }
}

C++

#include<iostream>
using namespace std;
#include<string.h>
typedef long long int ll;
ll ori[10] = {0, 1, 0, -1, 0, 1, 1, -1, -1, 1};
ll n, m;
char a[110][110];
bool vis[110][110];
ll cnt;

void dfs(ll x, ll y) {
    vis[x][y] = 1;
    for (int i = 0; i < 9; i++) {
        ll xx = x + ori[i];
        ll yy = y + ori[i+1];
        if(xx<1 || xx>n || yy<1 || yy>m)
            continue;
        if (a[xx][yy] == 'W' && !vis[xx][yy])
            dfs(xx, yy);
    }
}
int main() {
    cin >> n >> m;
    memset(vis, 0, sizeof(vis));
    cnt = 0;
    
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin >> a[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(a[i][j]=='W' && !vis[i][j]) {
                dfs(i,j);
                cnt++;
            }
        }
    }
    printf("%lld\n",cnt);
}

J - 二叉树先序遍历

输入一个整数n(n <= 100000)，表示二叉树中节点个数，编号为1~n。约定1号节点为二叉树的根节点。然后输入n行，每行包括两个整数，第i行表示编号为i的节点的左子节点和右子节点的编号。如果某个节点没有左子节点,那么对应输行的第一个整数为0;如果某个节点没有右子节点，那么对应行的第二个整数为0。

先序遍历输出此二叉树每个节点的编号，每行输出一个编号。

先序遍历(DLR)，是二叉树遍历的一种，也叫做先根遍历、前序遍历、前序周游，可记做根左右。前序遍历首先访问根节点然后遍历左子树，最后遍历右子树。

Java

import java.util.Scanner;

public class Main{
    static int l[], r[], res[];
    static int i = 0;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        l = new int[n+1];
        r = new int[n+1];
        res = new int[n+1];
        for (int j = 1; j <= n; j++) {
            l[j] = sc.nextInt();
            r[j] = sc.nextInt();
        }
        dfs(1);
        for (int j = 1; j <= n; j++) {
            System.out.println(res[j]);
        }
    }
    public static void dfs(int x) {
        res[++i] = x;
        if (l[x] > 0) {
            dfs(l[x]);
        }
        if (r[x] > 0) {
            dfs(r[x]);
        }
    }
}

C++

#include<iostream>
#include<cmath>
#include<string.h>
#include<algorithm>
#include<map>
#include<queue>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const int maxn=100100;
const int INF=pow(2,31)-1;
const int maxm=5e4+5;
const int mod=1000000007;
//vector<ll> g[maxn];
ll n;
ll l[maxn],r[maxn];
ll cnt=0;
ll st[maxn];
void dfs(ll x){
    st[++cnt]=x;
    if(l[x]){
        dfs(l[x]);
    }
    if(r[x]){
        dfs(r[x]);
    }
    return ;
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        ll x,y;
        cin>>x>>y;
        l[i]=x;
        r[i]=y;
    }
    dfs(1);
    for(int i=1;i<=cnt;i++){
        cout<<st[i]<<endl;
    }
    cout<<endl;
    return 0;
}

K - 迷宫（一）

3 4
S**.
....
***T

yes

Java

import java.util.Scanner;

public class Main{
    static int n, m, ex, ey;
    static char arr[][];
    static int[] ori = {0, 1, 0, -1, 0};
    static boolean flag;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        arr = new char[n][m];
        int x = 0, y = 0;
        sc.nextLine();
        for (int i = 0; i < n; i++) {
            String s = sc.next();
            if (s.contains("S")) {
                x = i;
                y = s.indexOf("S");
            }
            if (s.contains("T")) {
                ex = i;
                ey = s.indexOf("T");
            }
            arr[i] = s.toCharArray();
        }
        dfs(x, y);
        if (flag) {
            System.out.println("yes");
        } else {
            System.out.println("no");
        }
    }
    public static void dfs(int x, int y) {
        if (x == ex && y == ey) {
            flag = true;
            return;
        }
        arr[x][y] = '*';
        for (int i = 0; i < 4; i++) {
            int xx = x + ori[i];
            int yy = y + ori[i+1];
            if (xx < 0 || yy < 0 || xx >= n || yy >= m || arr[xx][yy] == '*')
                continue;
            dfs(xx, yy);
        }
    }
}

L - 马走日

马在中国象棋以日字形规则移动。请编写一段程序，给定n*m大小的棋盘，以及马的初始位置(x，y)，要求不能重复经过棋盘上的同一个点，计算马可以有多少途径遍历棋盘上的所有点。

Java

马走日问题（Java版）

C++

#include<iostream>
using namespace std;
#include<string.h>

int t, n, m, a, b, sum;
bool vis[6][6];

int orient[9] = {-1, 2, 1, -2, -1, -2, 1, 2, -1};  // 8个方向

void dfs(int x, int y, int curSum) {
    if (curSum == n*m) {
        sum++;
        return;
    }
    // 递归8个方向
    for (int i = 0; i < 8; i++) {
        // 获取可以到达的新方向
        int u = x + orient[i];
        int v = y + orient[i+1];
        // 剪枝条件，避免无效递归
        if (u < 0 || u >= n || v < 0 || v >= m || vis[u][v])
            continue;
        // 标记当前位置已访问
        vis[u][v] = true;
        // 继续往深处递归
        dfs(u, v, curSum+1);
        // 回溯
        vis[u][v] = false;
    }
}

int main() {
    cin >> t;
    while (t--) {
        cin >> n >> m >> a >> b;
        memset(vis, 0, sizeof(vis));
        sum = 0;
        vis[a][b] = 1;
        dfs(a, b, 1);
        cout << sum << endl;
    }
}

M - 八皇后问题

1
 1  2  3  4  5  6  7  8
 9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
48 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64

260

需要判断对角线abs(i-x)==abs(j-y)，以及记录八个棋子的坐标：l[i]、r[i]

Java

洛谷 P1219 [USACO1.5]八皇后 Checker Challenge（Java版）

C++

#include<iostream>
#include<cmath>
#include<string.h>
#include<algorithm>
#include<map>
#include<queue>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const int maxn=100100;
const int INF=pow(2,31)-1;
const int maxm=5e4+5;
const int mod=1000000007;
//vector<ll> g[maxn];
ll n;
ll a[110][110],b[110][110];
ll l[110],r[110];
ll cnt;
ll ma=0;
ll judge(ll x,ll y){
    for(int i=1;i<=8;i++){
        for(int j=1;j<=8;j++){
            if(b[i][j]){
                if((i==x)||(j==y)){
                    return 0;
                }
                if(abs(i-x)==abs(j-y))return 0;
            }
        }
    }
    return 1;
}
void dfs(ll step,ll s){
    if(s>=8){
        ll sum=0;
        for(int i=0;i<step;i++){
            sum+=a[l[i]][r[i]];
        }
        //cout<<sum<<endl;
        ma=max(sum,ma);
        return ;
    }
    if(step>8)return ;
    ll f=0;
    for(int i=1;i<=8;i++){
        if(judge(step,i)){
            b[step][i]=1;
            l[s]=step;
            r[s]=i;
            dfs(step+1,s+1);
            b[step][i]=0;
        }
    }
    dfs(step+1,s);
    return ;
}
int main(){
    cin>>n;
    while(n--){
        for(int i=1;i<=8;i++){
            for(int j=1;j<=8;j++){
                cin>>a[i][j];
            }
        }
        dfs(1,0);
        cout<<ma<<endl;
        ma=0;
        memset(b,0,sizeof(b));
    }
    return 0;
}

N - 选数

4 3
3 7 12 19

1

Java

思路：全排列问题改变，每次从出发点往后选择数据，确保种类不重复，即避免出现结果编号重复

import java.util.Scanner;

public class Main {
    static boolean[] vis;
    static int[] arr;
    static int cnt, n, m;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        arr = new int[n+1];
        vis = new boolean[n+1];
        for (int i = 1; i <= n; i++) {
            arr[i] = sc.nextInt();
        }
        dfs(0, 0, 0);
        System.out.println(cnt);
    }
    public static void dfs(int step, int sum, int s) {
        if (s == m) {
            if (judge(sum)) {
                cnt++;
            }
        }
        if (step > n)
            return;
        for (int i = step + 1; i <= n; i++) {
            if (vis[i])
                continue;
            vis[i] = true;
            dfs(i, sum + arr[i], s+1);
            vis[i] = false;
        }
    }
    public static boolean judge(int sum) {
        if (sum == 1)
            return false;
        for (int i = 2; i * i <= sum; i++) {
            if (sum % i == 0)
                return false;
        }
        return true;
    }
}

C++

#include<iostream>
#include<cmath>
#include<string.h>
#include<algorithm>
#include<map>
#include<queue>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const int maxn=100100;
const int INF=pow(2,31)-1;
const int maxm=5e4+5;
const int mod=1000000007;
ll n,m;
ll a[110];
ll b[110];
ll cnt;
bool judge(ll x){
    if(x==1)return false;
    for(int i=2;i*i<=x;i++){
        if(x%i==0)return false;
    }
    return true;
}
void dfs(ll step,ll sum,ll s){
    if(s==m){
        if(judge(sum)){
            cnt++;
            /*for(int i=1;i<=n;i++){
                if(b[i]){
                    cout<<i<<" ";
                }
            }
            cout<<endl;*/
            //cout<<sum<<endl;
        }
    }
    if(step>n)return ;
    for(int i=step+1;i<=n;i++){//防止重复
        if(b[i])continue;
        //sum+=a[i];
        b[i]=1;
        dfs(i,sum+a[i],s+1);
        b[i]=0;
    }
    return ;
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    dfs(0,0,0);
    printf("%lld\n",cnt);
    return 0;
}

O - 打开灯泡 Switch the Lamp On

达达是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女翰翰，从而被收留在地球上。

翰翰的家里有一辆飞行车。

有一天飞行车的电路板突然出现了故障，导致无法启动。

电路板的整体结构是一个R行C列的网格（R,C≤500），如下图所示。

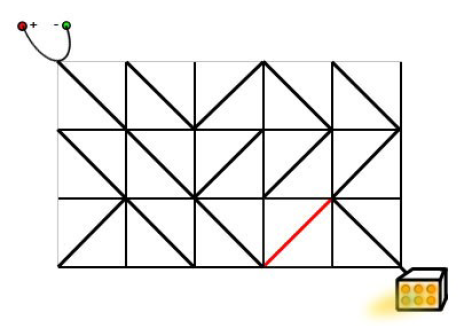
样例输入
3 5
\\/\\
\\///
/\\\\
样例输出
1

思路：最短路径策略，将二维表格离散化，可以到达的点进行连接，构成无向图，将原本达到的边代价设为0，反转90度之后的边代价设为1，找最短路径即可。

C++

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
typedef pair<ll,ll> P;
const int maxn=100100;
const int inf=0x3f3f3f3f3f;
const int maxm=5e4+5;
const int mod=1000000007;
ll n,m;
char a[510][510];
ll cnt[510][510];
ll tot;
ll d[510*510];
ll  vis[510*510];
struct node{
    ll to;
    ll w;
};
vector<node> g[510*510];
void dij(){
    priority_queue<P,vector<P>,greater<P> > que;
    for(int i=0;i<=tot+10;i++) d[i]=inf;
    ll s=1;
    d[s]=0;
    que.push({d[s],s});
    while(!que.empty()){
        P p=que.top();
        que.pop();
        ll u=p.second;
        //cout<<u<<endl;
        //ll v=p.first;
        if(p.first>d[u])continue;
        //vis[u]=1;
        for(int i=0;i<g[u].size();i++){
            node e=g[u][i];
            //cout<<e.to<<" ";
            if(d[e.to]>d[u]+e.w){
                d[e.to]=d[u]+e.w;
                que.push({d[e.to],e.to});
                //cout<<e.to<<endl;
            }

        }
        //cout<<endl;
    }
    if(d[tot]==inf){
        cout<<"NO SOLUTION";
    }else{
        cout<<d[tot];
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=n+1;i++){
        for(int j=1;j<=m+1;j++){
            cnt[i][j]=++tot;
        }
    }//离散化
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(a[i][j]=='\\'){//无向图
                g[cnt[i][j]].push_back({cnt[i+1][j+1],0});
                g[cnt[i+1][j+1]].push_back({cnt[i][j],0});
                g[cnt[i][j+1]].push_back({cnt[i+1][j],1});//旋转90度
                g[cnt[i+1][j]].push_back({cnt[i][j+1],1});
            }else{
                g[cnt[i][j]].push_back({cnt[i+1][j+1],1});
                g[cnt[i+1][j+1]].push_back({cnt[i][j],1});
                g[cnt[i][j+1]].push_back({cnt[i+1][j],0});//旋转90度
                g[cnt[i+1][j]].push_back({cnt[i][j+1],0});
            }
        }
    }
    dij();
    return 0;
}