提示:本次博文进行解答的问题列表
6.汉明距离
7.消失的数字
8.二进制中1的个数
9.0~n-1中缺失的数字
10.前n个数字二进制中1的个数
11.只出现一次的数字I
12.只出现一次的数字II
13.只出现一次的数字III
14.只出现一次的数字IV
前言
提示:此次博文是位运算的合集之一,新的小伙伴想要看其他关于位运算的内容可以看看之前的博客!
提示:以下是本篇文章正文内容,下面案例可供参考
六、汉明距离
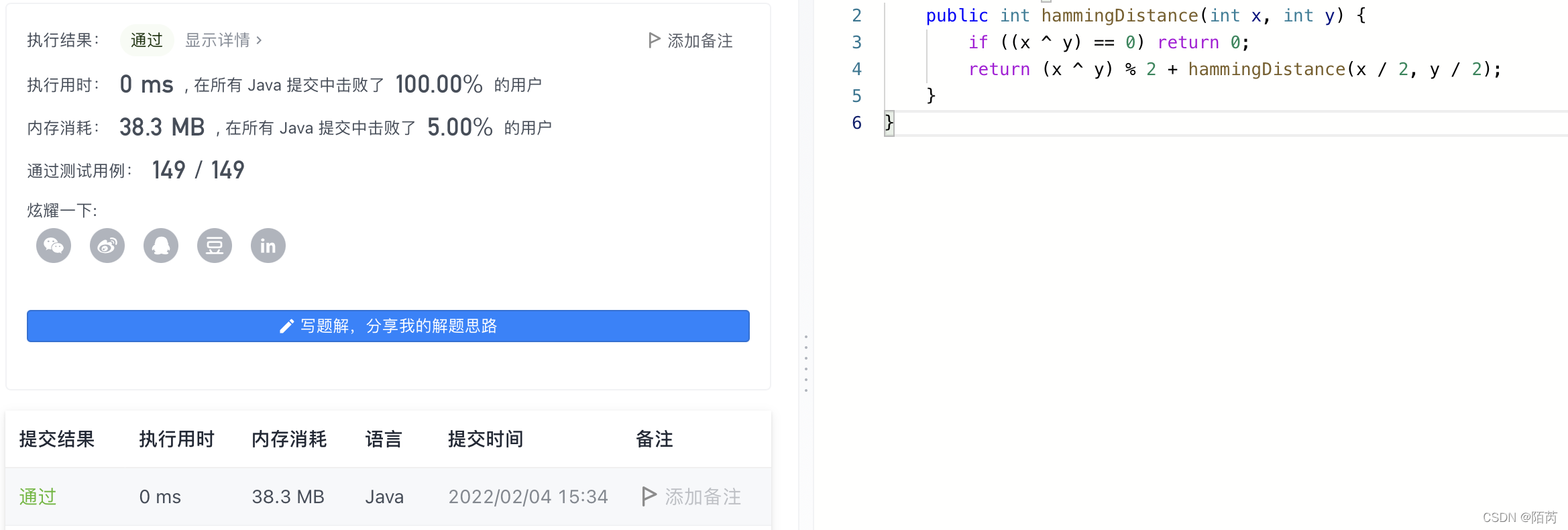
0、代码运行结果:
1.题目描述:
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
输入:x = 1, y = 4
输出:2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
示例 2:
输入:x = 3, y = 1
输出:1
提示:
0 <= x, y <= 2^31 - 1
2.代码如下:
public int hammingDistance(int x, int y) {
if ((x ^ y) == 0) return 0;
return (x ^ y) % 2 + hammingDistance(x / 2, y / 2);
}
3.代码解析:
public int hammingDistance(int x, int y) {
if ((x ^ y) == 0) return 0;
//如果x == y , 那么汉明距离为0;
return (x ^ y) % 2 + hammingDistance(x / 2, y / 2);
//如果x != y ,那么进行递归(x ^ y) % 2 + hammingDistance(x / 2, y / 2);
//实例解析:
//输入:x = 1, y = 4
//输出:2
//解释:
//1 (0 0 0 1)
//4 (0 1 0 0)
↑ ↑
//上面的箭头指出了对应二进制位不同的位置。
//return (1 ^ 4) % 2 == 5(二进制为:0101) % 2 == 1
// + hammingDistance(x / 2, y / 2) 相当于将x和y的二进制位右移一位
//然后进行
//return*(0 ^ 2) % 2 == 2(二进制位为:0010) % 2 == 0
//......
//总结
//就是每次异或一下,然后判断二进制第零位为一还是为零,是一的话汉明距离加一。
//其实可以将代码简化为如下代码:(运行时间也是100%,小伙伴们可以测试哦!)
// int res = 0;
// while((x ^ y) != 0)
// {
// res += (x ^ y) & 1;
// x >>= 1;
// y >>= 1;
// }
// return res;
//
}
七.消失的数字
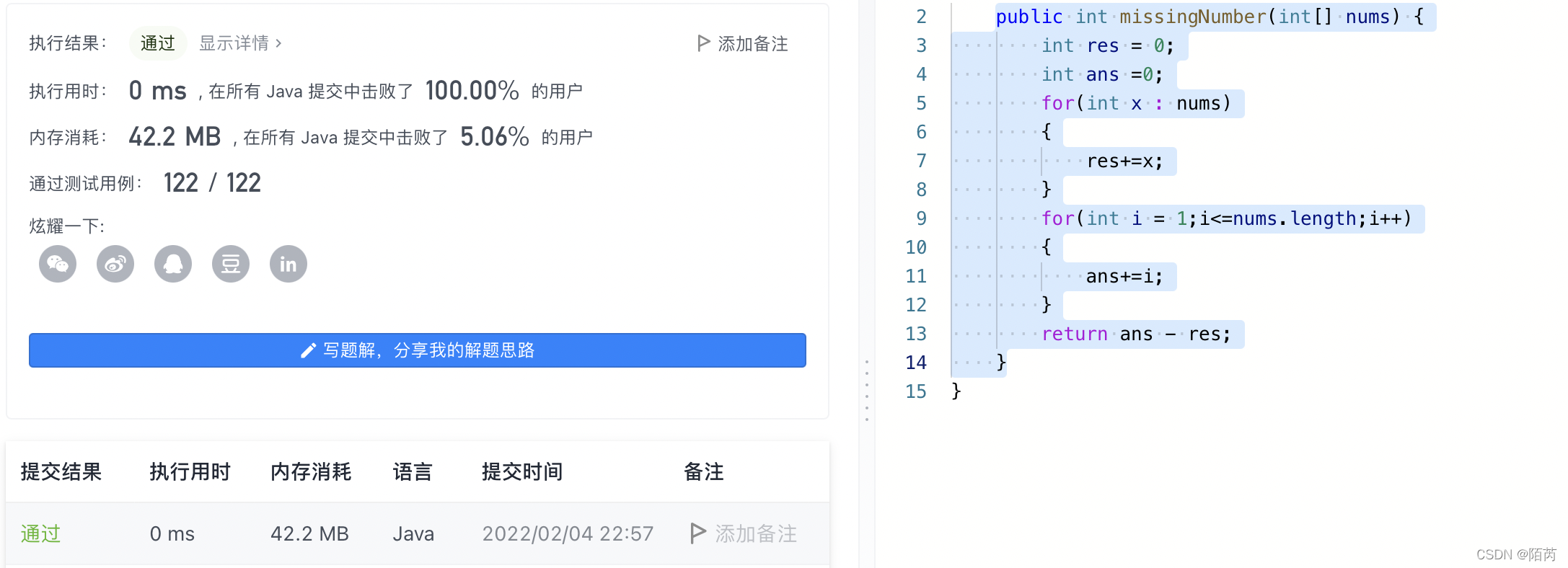
0、代码运行结果:
1.题目描述:
数组nums包含从0到n的所有整数,但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗?
示例 1:
输入:[3,0,1]
输出:2
示例 2:
输入:[9,6,4,2,3,5,7,0,1]
输出:8
2.代码如下:
public int missingNumber(int[] nums) {
int res = 0;
int ans =0;
for(int x : nums)
{
res+=x;
}
for(int i = 1;i<=nums.length;i++)
{
ans+=i;
}
return ans - res;
}
3.代码解析:
public int missingNumber(int[] nums) {
int res = 0;
int ans =0;
//题目所给范围是[0~n]之间的数
//所以题目思路是进行一次for循环将[0~n]之间的数进行相加,然后减去所给nums数组中所给数字的和,最后进行相减,得出最终答案。
//首先定义两个变量用来计数
for(int x : nums)//用res变量来记录nums数组中所给数字的和
{
res+=x;
}
for(int i = 1;i<=nums.length;i++)//用ans变量来记录[0~n]范围中数字的和
{
ans+=i;
}
return ans - res;//[0~n]范围中数字的和 减去 nums数组中所给数字的和即为最终答案。
}
八. 二进制中1的个数
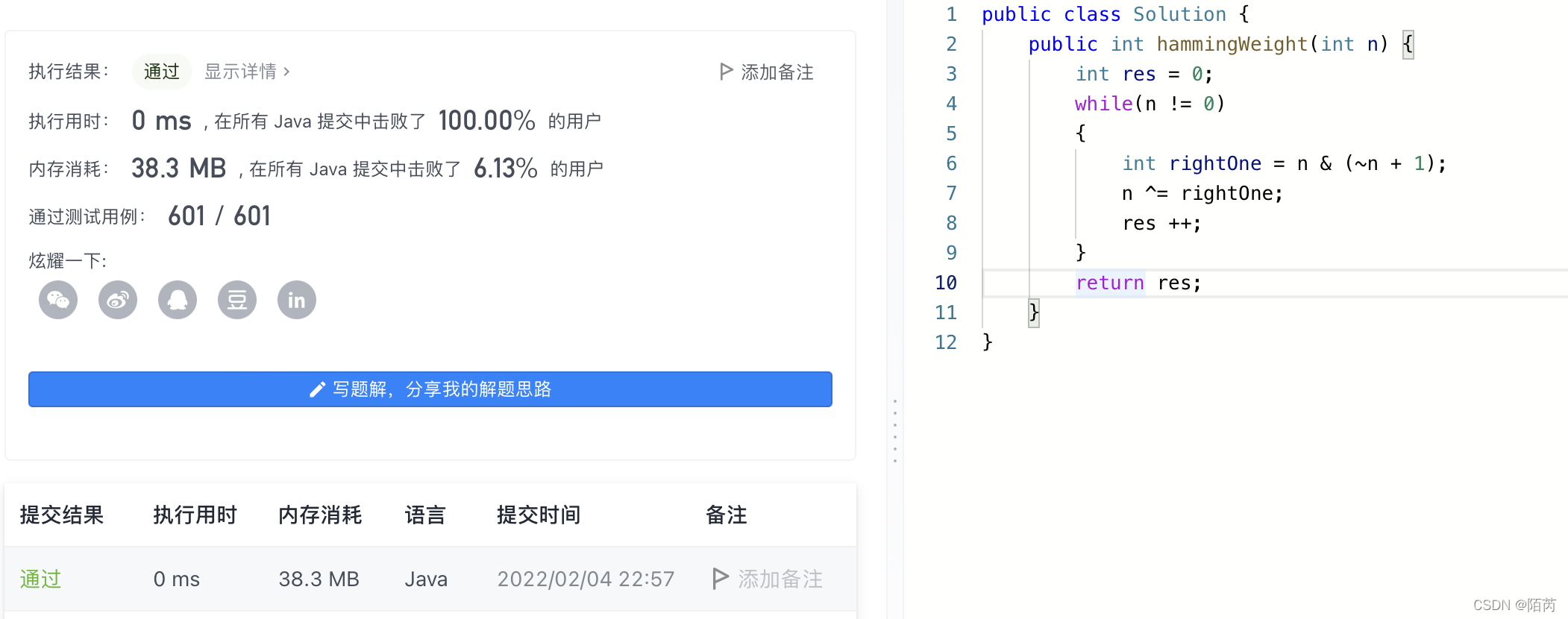
0、代码运行结果:
1.题目描述:
编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中数字位数为 '1' 的个数(也被称为 汉明重量).)。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用 二进制补码 记法来表示有符号整数。因此,在上面的 示例 3 中,输入表示有符号整数 -3。
示例 1:
输入:n = 11 (控制台输入 00000000000000000000000000001011)
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 '1'。
示例 2:
输入:n = 128 (控制台输入 00000000000000000000000010000000)
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 '1'。
示例 3:
输入:n = 4294967293 (控制台输入 11111111111111111111111111111101,部分语言中 n = -3)
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 '1'。
提示:
输入必须是长度为 32 的 二进制串 。
2.代码如下:
public int hammingWeight(int n) {
int res = 0;
while(n != 0)
{
int rightOne = n & (~n + 1);
n ^= rightOne;
res ++;
}
return res;
}
3.代码解析:
public int hammingWeight(int n) {
int res = 0;
//题目是让我们求所给数字在二进制表示的情况下,“1”的出现次数,
//本题思路:我们每次拿出所给数字最右侧的“1”,然后将最右侧的“1”删除,直到所给数字为0
//本题难点:如何取最右侧的“1”。
while(n != 0)
{
int rightOne = n & (~n + 1);
//我们定义变量rightOne用来记录最右侧的“1”,
//取指定数字n中最右侧的“1”的方式是:n & (~n + 1)
//代码不长,建议背下来即可
//实例解析:
//输入:n = 11 (11的二进制表示为:00000000000000000000000000001011)
//输出:3
//为了方便观看,我们取最后8位,11的二进制表示为:00001011
//首先进行取反:~n :11110100
//然后进行取反加一: ~n+1 :11110101
//然后进行与操作:n & (~n + 1) : 0000001
//最后最右侧的“1”被取出
n ^= rightOne;
//现在我们需要将制定数字中的最右侧的“1”去掉,因为已经计算过了
//此时我们可以用异或操作,因为异或操作是二进制位中相同为0,不同为一
res ++;
}
return res;
}
九.0~n-1中缺失的数字
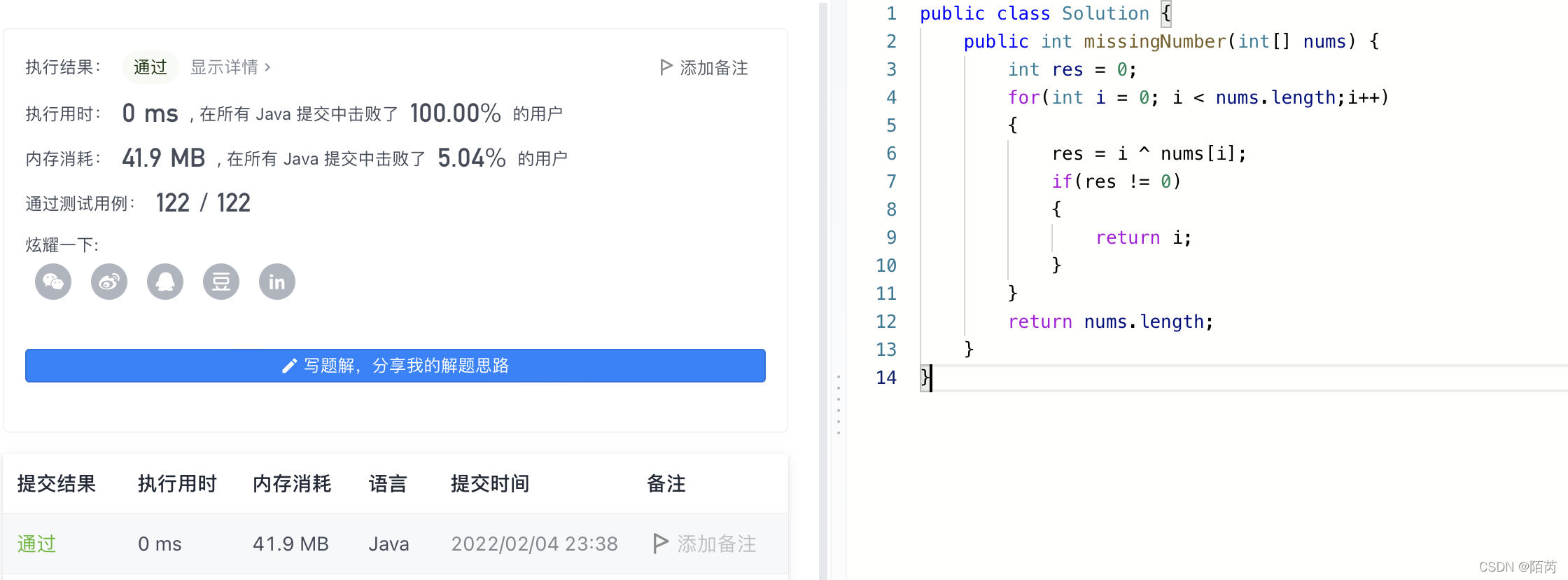
0、代码运行结果:
1.题目描述:
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字。
示例 1:
输入: [0,1,3]
输出: 2
示例 2:
输入: [0,1,2,3,4,5,6,7,9]
输出: 8
限制:
1 <= 数组长度 <= 10000
2.代码如下:
public int missingNumber(int[] nums) {
int res = 0;
for(int i = 0; i < nums.length;i++)
{
res = i ^ nums[i];
if(res != 0)
{
return i;
}
}
return nums.length;
}
3.代码解析:
public int missingNumber(int[] nums) {
//由题目可知,我们需要求出[0~n]范围中缺失的某个数字
//本题思路,进行一次for循环,因为是递增数组所以不需要进行排序
//我们可以采用相同数字异或为0,进行判断
int res = 0;
for(int i = 0; i < nums.length;i++)
{
res = i ^ nums[i];
//实例解析
//示例 1:
//输入: [0,1,3]
//输出: 2
//i == 0 : 0 ^ 0 == 0;
//i == 1 : 1 ^ 1 == 0;
//i == 2 : 2 ^ 3 == 1;
if(res != 0)//如果res不为0,说明出现缺失的数字了。
{
return i;
}
}
return nums.length;
}
十.前n个数字二进制中1的个数
0、代码运行结果:
1.题目描述:
给定一个非负整数 n ,请计算 0 到 n 之间的每个数字的二进制表示中 1 的个数,并输出一个数组。
示例 1:
输入: n = 2
输出: [0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
示例 2:
输入: n = 5
输出: [0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
说明 :
0 <= n <= 10^5
2.代码如下:
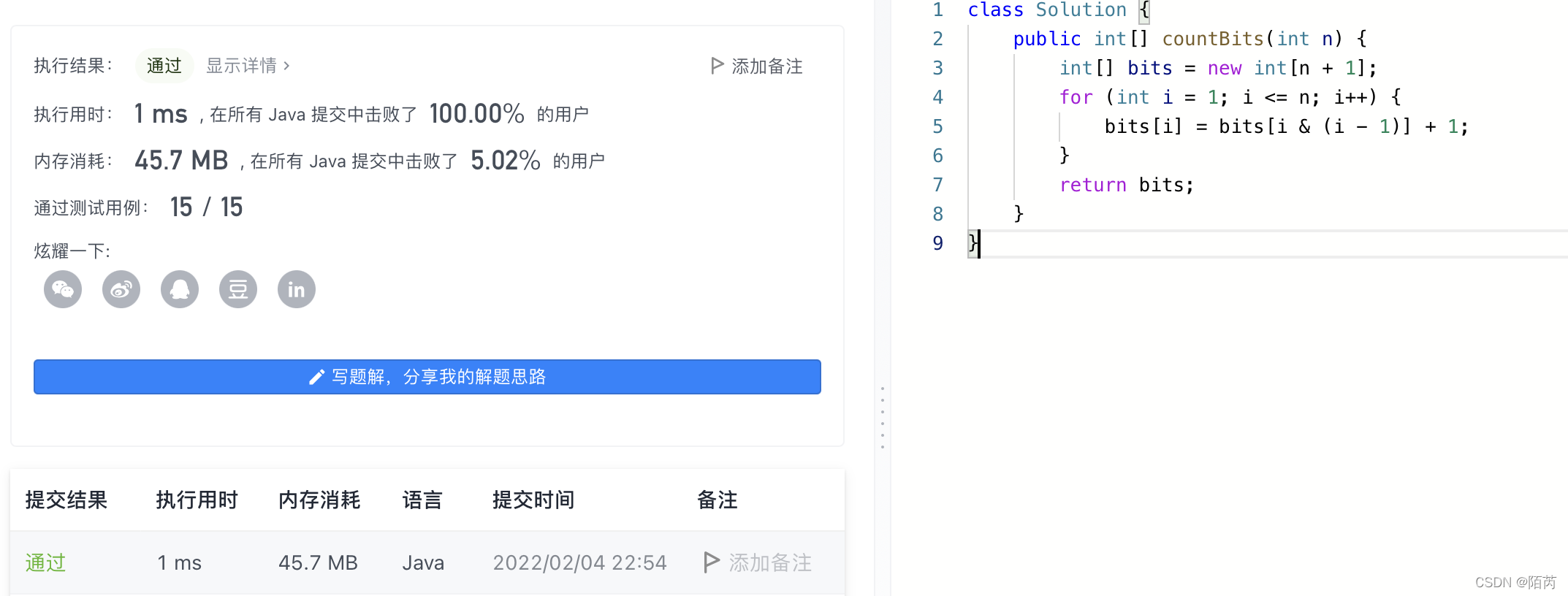
public int[] countBits(int n) {
int[] bits = new int[n + 1];
for (int i = 1; i <= n; i++) {
bits[i] = bits[i & (i - 1)] + 1;
}
return bits;
}
3.代码解析:
//采用一个数组进行计数,名称为bit数组
//对于正整数n,将n的二进制表示右移一位,等价于将其二进制表示的最低位去掉,得到的数是n/2
//如果bit[n/2]的值已经知道,那么从bit[n/2]的值推算出bit[n]的值
//由此,可以将正整数n分为两类,一是奇数,二是偶数
//有如下公式,
//1 所给数字n为奇数,bit[n] = bit[n/2] + 1
//2 所给数字n为偶数,bit[n] = bit[n/2]
//综上所述,我们可以将公式1和公式2综合在一起,最后的表达式为bit[n/2] + n % 2。
public int[] countBits(int n) {
int[] bits = new int[n + 1];
for (int i = 1; i <= n; i++) {
bits[i] = bits[i & (i - 1)] + 1;
}
return bits;
}
//我们以示例2进行解析
//根据示例我们可以得出,所需要求的比特位长度为n+1,因为二进制是从下标0开始算起
//示例 2:
//输入:n = 5
//输出:[0,1,1,2,1,2]
//解释:
//0 --> 0
//1 --> 1
//2 --> 10
//3 --> 11
//4 --> 100
//5 --> 101
//首先申请一个长度为n+1的bit数组
//进行for循环
//i == 0 ,bits[0] = 0;
//i == 1 时,bits[1] = bits[0] + (1 & 1) == 0 + 1 = 1;
//i == 2 时,bits[2] = bits[1] + (2 & 1) == 1 + 0 = 1;
//i == 3 时,bits[3] = bits[1] + (3 & 1) == 1 + 1 = 2;
//i == 4 时,bits[4] = bits[2] + (4 & 1) == 1 + 0 = 1;
//i == 5 时,bits[5] = bits[2] + (5 & 1) == 1 + 1 = 2;
//返回bit数组,bit数组为[0, 1, 1, 2, 1, 2]。
十一.只出现一次的数字I
0、代码运行结果:
1.题目描述:
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
2.代码如下:
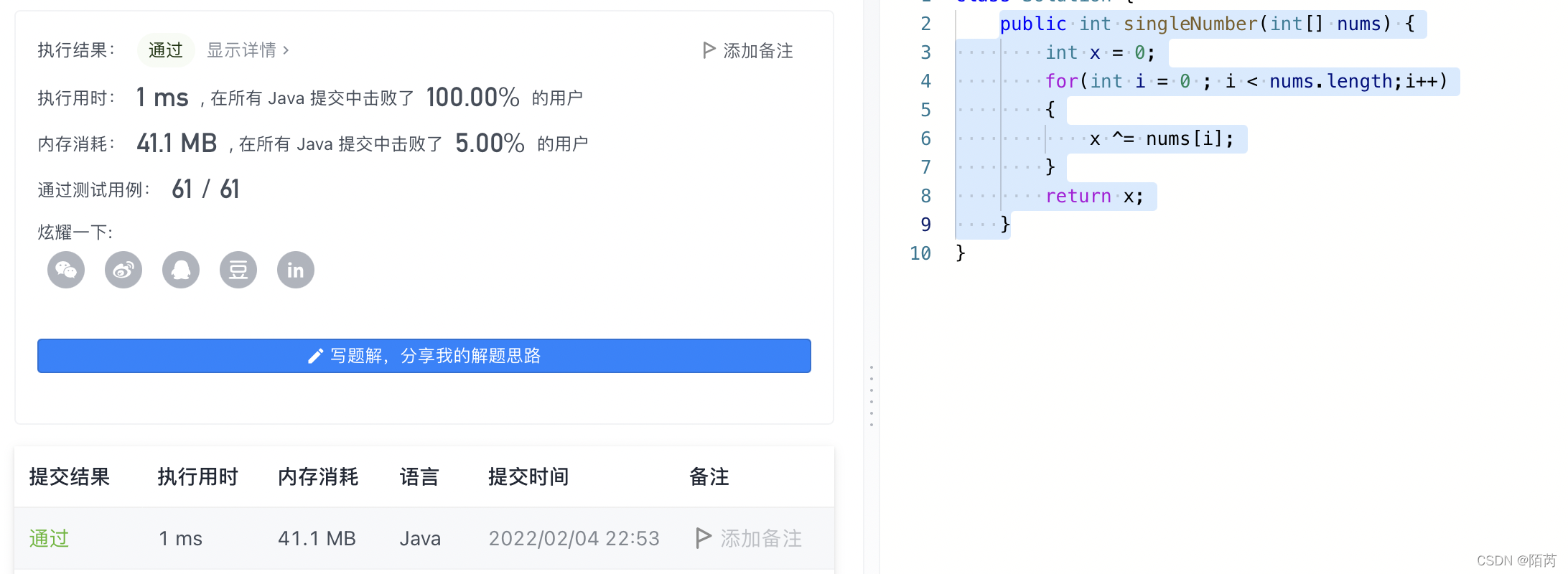
public int singleNumber(int[] nums) {
int x = 0;
for(int i = 0 ; i < nums.length;i++)
{
x ^= nums[i];
}
return x;
}
3.代码解析:
public int singleNumber(int[] nums) {
int x = 0;
//由题目可知,只有一个数字出现一次,剩下的数字都出现了两次
//由位运算中的异或操作,即相同数字异或为0,并且异或操作满足数学上的交换律和结合律。
//所以进行一次for循环,用变量x进行记录。循环结束后,x即为只出现一次的数字。
for(int i = 0 ; i < nums.length;i++)
{
//实例解析:
//示例 2:
//输入: [4,1,2,1,2]
//输出: 4
//i == 0 : x = 0 ^ 4 == 4
//i == 1 : x = 4 ^ 1 == 5
//i == 2 : x = 5 ^ 2 == 7
//i == 3 : x = 7 ^ 1 == 6
//i == 4 : x = 6 ^ 2 == 4
x ^= nums[i];
}
return x;
}
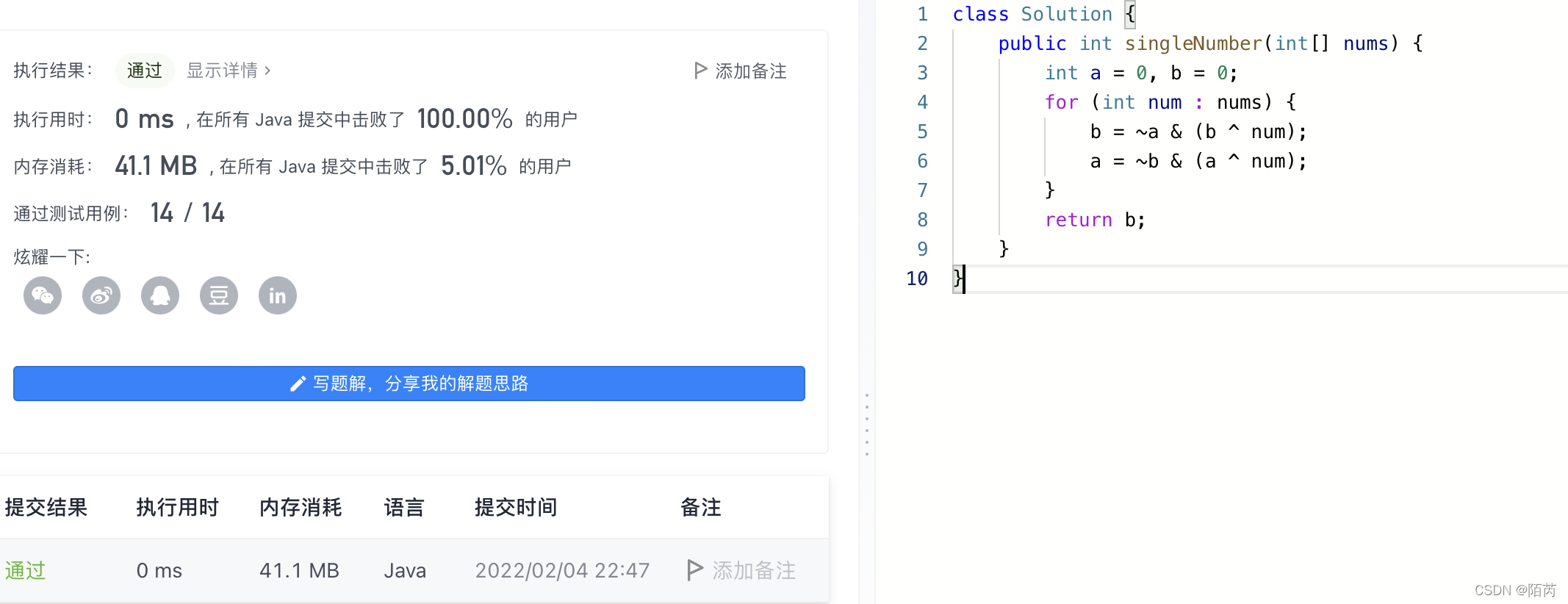
十二.只出现一次的数字II
0、代码运行结果:
1.题目描述:
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
2.代码如下:
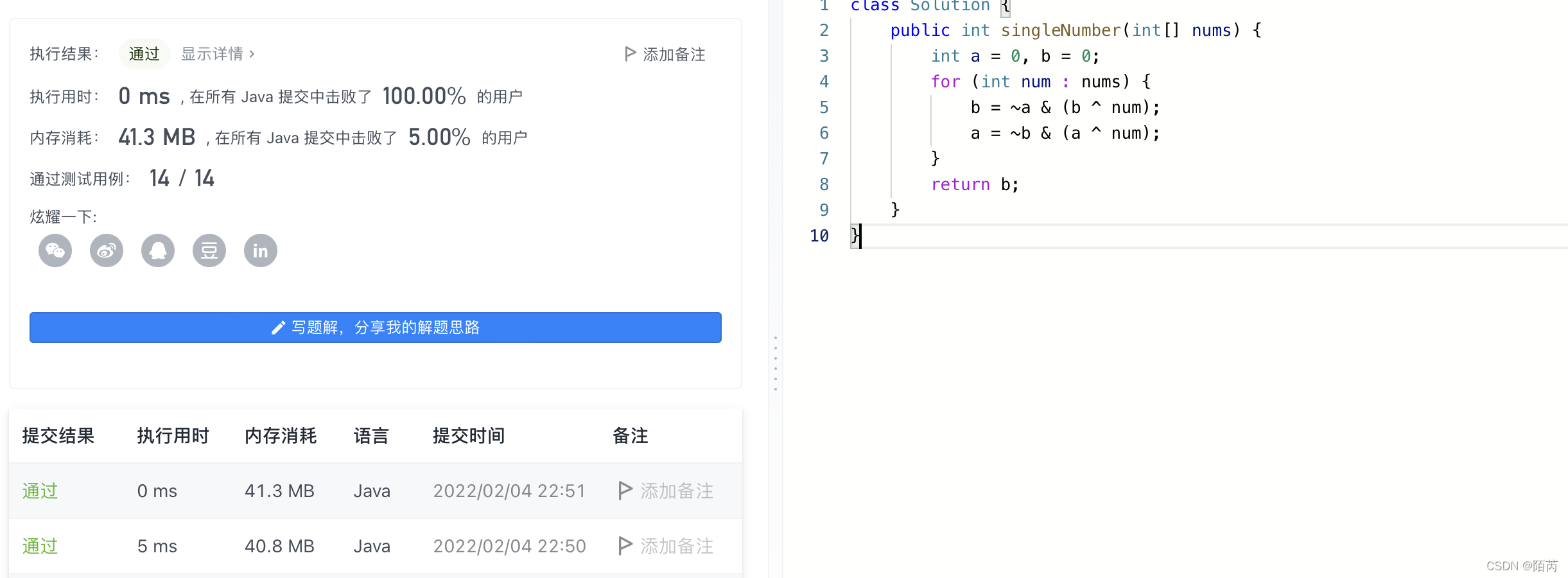
public int singleNumber(int[] nums) {
int a = 0, b = 0;
for (int num : nums) {
b = ~a & (b ^ num);
a = ~b & (a ^ num);
}
return b;
}
3.代码解析:
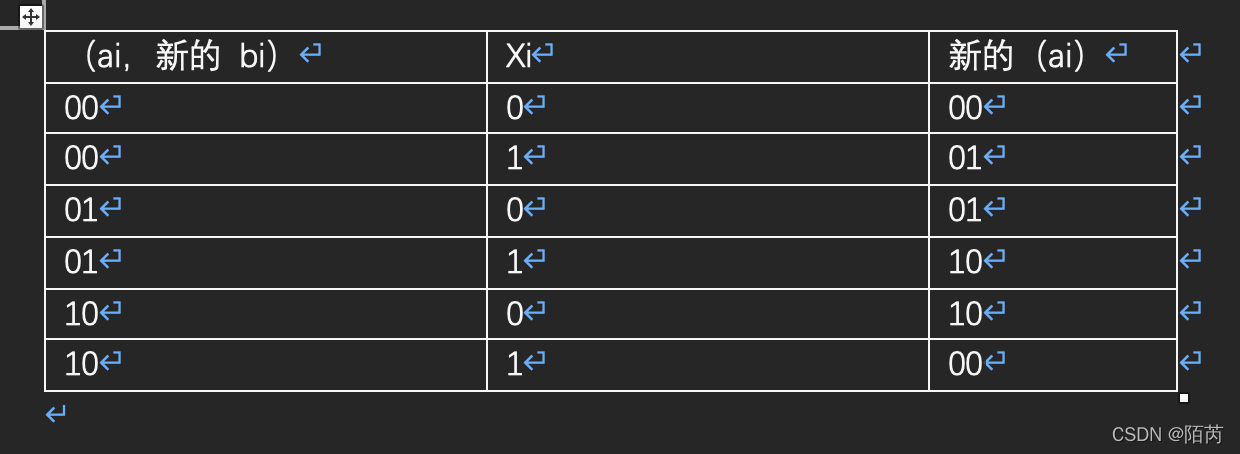

图片1:

图片2:

图片3:

图片4:

public int singleNumber(int[] nums) {
//两个整数a和b,会有三种情况:
//a 的第i 位为0 且b 的第i 位为0,表示0。
//a 的第i 位为0 且b 的第i 位为1,表示1。
//a 的第i 位为1 且b 的第i 位为0,表示2。
//当我们遍历到一个新的整数x时,对于x的第i位xi,如果 xi=0,那么a和b的第i位不变;
//如果xi=1,那么a和b的第i位按照 (00)→(01)→(10)→(00)→(01)→(10)→(00) 这一循环进行变化。
//可以推导出如下两个公式:
//在图片1和2
//综合这两个公式可以推导出最后结论,如图三。
//将图片三在进行优化,得到图片4。
int a = 0, b = 0;
for (int num : nums) {
b = ~a & (b ^ num);
a = ~b & (a ^ num);
}
return b;
//实例解析
//示例 1:
//输入:nums = [2,2,3,2]
//输出:3
//进入for循环:
//i == 0:
//b = -1 & (0 ^ 2) = 2;
//a = -3 & (0 ^ 2) = 0;
//i == 1:
//b = -1 & (2 ^ 2) = 0;
//a = -1 & (0 ^ 2) = 2;
//i == 2:
//b = -3 & (0 ^ 3) = 1;
//a = -2 & (2 ^ 3) = 0;
//i == 3:
//b = -1 & (1 ^ 2) = 3;
//a = -4 & (0 ^ 2) = 0;
}
十三.只出现一次的数字III
0、代码运行结果:

1.题目描述:
给定一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
进阶:你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现?
示例 1:
输入:nums = [1,2,1,3,2,5]
输出:[3,5]
解释:[5, 3] 也是有效的答案。
示例 2:
输入:nums = [-1,0]
输出:[-1,0]
示例 3:
输入:nums = [0,1]
输出:[1,0]
2.代码如下:
public int[] singleNumber(int[] arr) {
int eor = 0;
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
}
int rightOne = eor & (~eor + 1);
int onlyOne = 0;
for (int i = 0 ; i < arr.length;i++) {
if ((arr[i] & rightOne) != 0) {
onlyOne ^= arr[i];
}
}
return new int[]{onlyOne, eor ^ onlyOne};
}
3.代码解析:
public int[] singleNumber(int[] arr) {
int eor = 0;
for (int i = 0; i < arr.length; i++) {
eor ^= arr[i];
}
// eor = a ^ b
// eor != 0
// eor必然有一个位置上是1
// 0110010000
// 0000010000
int rightOne = eor & (~eor + 1); // 提取出最右的1
int onlyOne = 0; // eor'
for (int i = 0 ; i < arr.length;i++) {
// arr[1] = 111100011110000
// rightOne= 000000000010000
if ((arr[i] & rightOne) != 0) {
onlyOne ^= arr[i];
}
}
//示例 1:
//输入:nums = [1,2,1,3,2,5]
//输出:[3,5]
//首先定义一个变量eor
//然后进行一次for循环,得到只出现一次的两个数的异或值
//进行如下for循环:
//for (int i = 0; i < arr.length; i++) {
// eor ^= arr[i];
//}
//eor = 0 ^ 1 ^ 2 ^ 1 ^ 3 ^ 2 ^ 5 = 6(二进制表示为:0110)
//然后我们提取出eor最右侧的1
//即rightOne = 0010 = 2;
//我们只让nums数组中数字的二进制在第一位为1的数进行异或操作
//1 : 0001
//2 : 0010
//3 : 0011
//5 : 0101
//进入如下for循环:
//for (int i = 0 ; i < arr.length;i++) {
// if ((arr[i] & rightOne) != 0) {
// onlyOne ^= arr[i];
// }
//}
//i == 0 : 1 & 2 == 0;跳过
//i == 1 : 2 & 2 == 2;onlyOne = 0 ^ 2 = 2;
//i == 2 : 1 & 2 == 0;跳过
//i == 3 : 3 & 2 == 2;onlyOne = 2 ^ 3 = 1;
//i == 4 : 2 & 2 == 2;onlyOne = 1 ^ 2 = 3;
//i == 5 : 5 & 2 == 0;跳过
//onlyOne = 3;
//eor ^ onlyOne = 3 ^ 6 = 5.
return new int[]{onlyOne, eor ^ onlyOne};
}
十四.只出现一次的数字IV
0、代码运行结果:
1.题目描述:
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,100]
输出:100
2.代码如下:
public int singleNumber(int[] nums) {
int a = 0, b = 0;
for (int num : nums) {
b = ~a & (b ^ num);
a = ~b & (a ^ num);
}
return b;
}
3.代码解析:


图片1:

图片2:

图片3:

图片4:

public int singleNumber(int[] nums) {
//两个整数a和b,会有三种情况:
//a 的第i 位为0 且b 的第i 位为0,表示0。
//a 的第i 位为0 且b 的第i 位为1,表示1。
//a 的第i 位为1 且b 的第i 位为0,表示2。
//当我们遍历到一个新的整数x时,对于x的第i位xi,如果 xi=0,那么a和b的第i位不变;
//如果xi=1,那么a和b的第i位按照 (00)→(01)→(10)→(00)→(01)→(10)→(00) 这一循环进行变化。
//可以推导出如下两个公式:
//在图片1和2
//综合这两个公式可以推导出最后结论,如图三。
//将图片三在进行优化,得到图片4。
int a = 0, b = 0;
for (int num : nums) {
b = ~a & (b ^ num);
a = ~b & (a ^ num);
}
return b;
//实例解析
//示例 1:
//输入:nums = [2,2,3,2]
//输出:3
//进入for循环:
//i == 0:
//b = -1 & (0 ^ 2) = 2;
//a = -3 & (0 ^ 2) = 0;
//i == 1:
//b = -1 & (2 ^ 2) = 0;
//a = -1 & (0 ^ 2) = 2;
//i == 2:
//b = -3 & (0 ^ 3) = 1;
//a = -2 & (2 ^ 3) = 0;
//i == 3:
//b = -1 & (1 ^ 2) = 3;
//a = -4 & (0 ^ 2) = 0;
}