[数据结构与算法]动态规划解决不同的子序列问题

问题描述：

(1)方法一：

状态：F(i,j): S[1:i]中的子串与T[1:j]相同的个数
递推公式： 在F(i,j)处需要考虑S[i] = T[j] 和 S[i] != T[j]两种情况
A.当S[i] = T[j]::
(1)让S[i]匹配T[j]则 F(i,j) = F(i-1,j-1)
(2)让S[i]不匹配T[j],则问题就变为S[1:i-1]中的子串与T[1:j]相同的个数，则 F(i,j) = F(i-1,j) 故S[i] = T[j]时F(i,j) = F(i-1,j-1) + F(i-1,j)
B.当S[i] != T[j]:
问题退化为S[1:i-1]中的子串与T[1:j]相同的个数 故,S[i] != T[j]时F(i,j) = F(i-1,j)
初始化：引入空串进行初始化 F(i,0) = 1 —> S的子串与空串相同的个数，只有空串与空串相同
返回结果：F(m,n)

代码：

import java.util.*;
public class Solution {
    /**
     * 
     * @param S string字符串 
     * @param T string字符串 
     * @return int整型
     */
    public int numDistinct (String S, String T) {
        // write code here
        int sLen=S.length();
        int tLen=T.length();
        int[][] numDis=new int[sLen+1][tLen+1];
        numDis[0][0]=1;
        // F(i,j)，初始化第一行剩余列的所有值为0
        for(int i=1;i <=tLen;i++){
            numDis[0][i]=0;
        }
        //F(i,0)=1
        for(int i=1;i<sLen;i++){
            numDis[i][0]=1;
        }
        for(int i=1;i<=sLen;i++){
            for(int j=1;j<=tLen;j++){
                // S的第i个字符与T的第j个字符相同
                if(S.charAt(i-1)==T.charAt(j-1)){
                    numDis[i][j]=numDis[i-1][j]+numDis[i-1][j-1];
                }else{
                    //S的第i个字符与T的第j个字符不相同 
                    //从S的前i-1个字符中找子串，使子串与T的前j个字符相同
                    numDis[i][j]=numDis[i-1][j];
                }
            }
        }
        return numDis[sLen][tLen];
    }
}

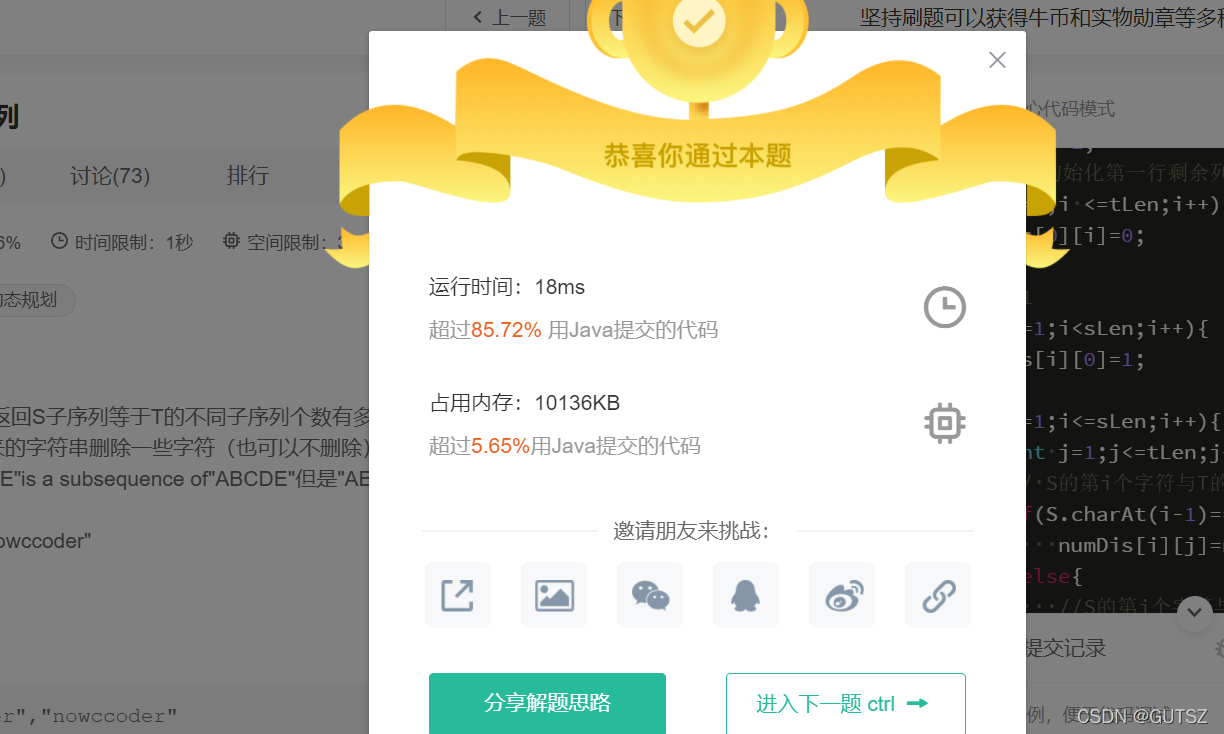
运行结果：

(2)方法二：

可优化空间复杂度为O(n)
f[i][j] 只和 f[i - 1][j], f[i - 1][j - 1]有关
可以用一维数组保存上一行的结果，每次从最后一列更新元素值

代码：

运行结果：