[数据结构与算法]240.食物链 (并查集扩展域带权拆点)

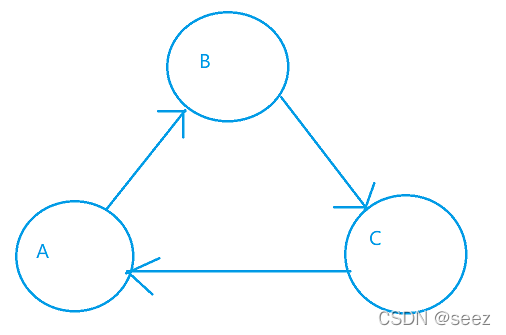
题意：只有三种动物，三种动物食物链关系如图

带权并查集

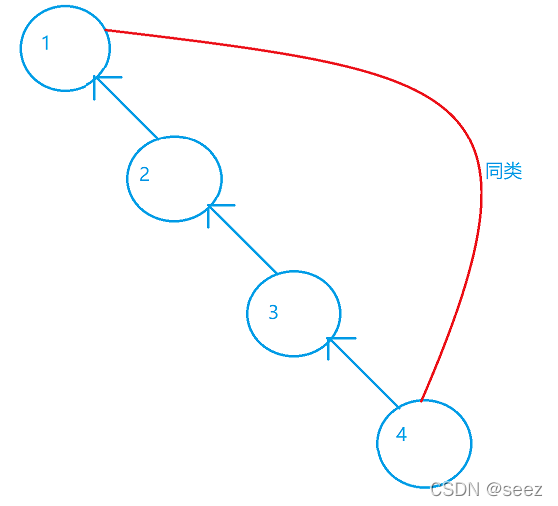
因为只有三种动物，他们和根结点的关系可以用距离来表示

设两个动物a,b ，可以根据他们差值模3的结果得出他们的关系

• (a-b)%3==0? ? ? ? ? ? ? ? 同类
• (a-b)%3==1? ? ? ? ? ? ? ? b吃a
• (a-b)%3==2? ? ? ? ? ? ? ? a吃b

那么可以得出，我们只要知道两个点之间的距离，就能推断出他们的关系，所以这样就可以用并查集的路径压缩，然后通过新开一个数组记录距离，就能推断出一个集合内各个点之间的关系

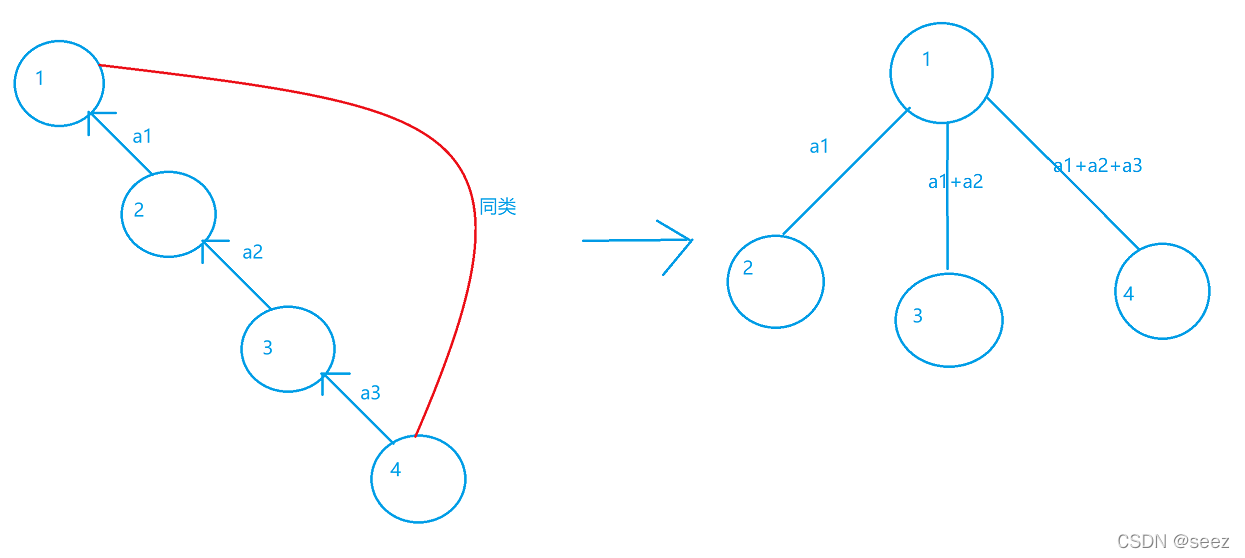
?那么路径压缩的时候，就应该是让 d[now]=d[now]+d[p[now]],然后再把所有的边连到根结点上面

int find(int x)
{
    if(p[x]!=x)
    {
        int u=find(p[x]);   //先递归计算出d[px]
        d[x]+=d[p[x]];        //d[x]=d[x]+d[px];计算出到根节点的距离
        p[x]=u;
    }
    return p[x];
}

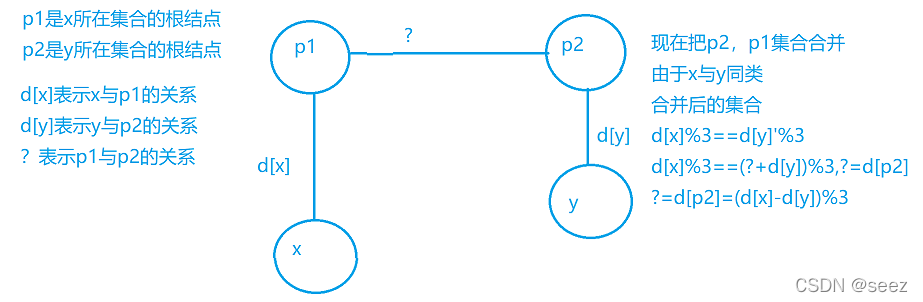
计算两个点的关系，合并两个点? x,y

x和y同类???????

• px == py? ? ? ? ? ? ? ? 有关系，判断是否同类? ? (d[x]-d[y])%3==0? ? ? ?
• px !=? py? ? ? ? ? ? ? ? 没有关系，可以合并? ? ? ? (d[p[y]]=d[x]-d[y])

x吃y

• px==py? ? ? ? ? ? ? ? 在同一集合中，判断是处理过了还是假话? ? ?d[x]%3==(d[y]+1)%3
• px!=py? ? ? ? ? ? ? ? ?不在同一集合中，处理一遍? ? ? ? ? ? ? ? ? ? ? ? ? d[py]=(d[x]-d[y]-1)

?

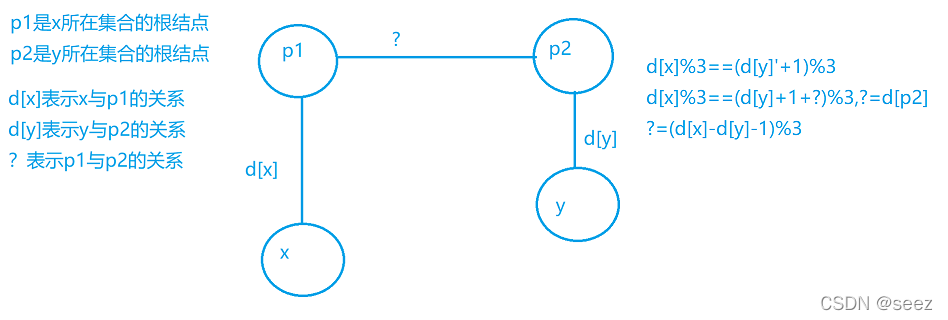
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1e5+10;
int p[N],d[N];

int find(int x)
{
    if(p[x]!=x)
    {
        int u=find(p[x]);   //先递归计算出d[px]
        d[x]+=d[p[x]];        //d[x]=d[x]+d[px];计算出到根节点的距离
        p[x]=u;
    }
    return p[x];
}

int main()
{
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=n;i++)
        p[i]=i;
    int res=0;
    while(k--)
    {
        int D,x,y;
        cin>>D>>x>>y;
        if(x>n||y>n)
        {
            res++;
            continue;
        }
        int px=find(x),py=find(y);
        if(D==1)    //是否同类
        {
            
            if(px==py&&(d[x]-d[y])%3)    //同一集合不同类,假话
                res++;
            else if(px!=py) //不同集合，合并一类
            {
                p[py]=px;
                d[py]=(d[x]-d[y]);
            }
        }
        else        //x吃y
        {
            if(px==py&&(d[x]-d[y]-1)%3)  //同一集合
                res++;
            else if(px!=py) //合并集合
            {
                p[py]=px;
                d[py]= d[x] -1 - d[y];
            }
        }
    }
    cout<<res;
    return 0;
}

由于本题只要知道是否是同类元素，而不用细分到同类中的各个元素，所以d数组其实就可以只有三种值0，1，2，根据0，1，2就可以分为三类

拆点并查集

对于任意一个点来说，他有三个集合

天敌域，捕食域，同类域

由于只有三种动物，所以不存在一个域里面有两种动物，所以我们可以以一个点为根结点构建他的

三个集合

#include <iostream>
#include <algorithm>
using namespace std;
const int N=2e5+10;
int p[N];
//x表示同类 x+n表示捕食  x+2n表示天敌
int find(int x)
{
    if(p[x]!=x)
        p[x]=find(p[x]);
    return p[x];
}
int merge(int x,int y)
{
    p[find(x)]=find(y);
}
int main()
{
    int res=0;
    int n,k;
    cin>>n>>k;
    for(int i=1;i<=3*n;i++)
        p[i]=i;
    while(k--)
    {
        int d,x,y;
        cin>>d>>x>>y;
        if(x>n||y>n) res++;
        else if(d==1)
        {   //x是y的天敌或者捕食者
            if(find(x)==find(y+n)||find(x)==find(y+2*n))
                res++;
            else
            {
                merge(x,y);
                merge(x+n,y+n);
                merge(x+n+n,y+n+n);
            }
        }
        else
        {   //x是y的同类或者捕食者，是假话
            if(find(x)==find(y)||find(x+2*n)==find(y))
                res++;
            else
            {
                merge(x,y+2*n);//x是y的天敌
                merge(x+n,y);   //x的捕食者是y
                merge(x+2*n,y+n);//x的天敌是y的捕食者
            }
        }
    }
    cout<<res;
    return 0;
}