砝码称重

首先想到的是直接爆搜，结果只过了样例，复杂度应该是 $n!$ ，所以妥妥超时。

int a[N],vis[N],n;
int ok[100010];
int sum;
void dfs(int cur,int x,int sign){
    cur+=sign*a[x];
    if(cur>0)ok[cur]=1;
    for(int i=1;i<=n;i++){
        if(!vis[i]){
            vis[i]=1;
            dfs(cur,i,1);
            dfs(cur,i,-1);
            vis[i]=0;
        }
    }
}

其实这个题很像背包，即看某个重量可不可以被满足，考虑dp。 $d p [i] [j]$ 表示枚举到第 $i$ 个砝码，重量 $j$ 是否可以获得。这是最基本最容易想到的状态转移方法，在空间允许的情况下，用一个维度枚举个数，用一个维度枚举答案。因为只要不使用当前的砝码 $i$ ，当前可以表示的重量和 $i ? 1$ 可以表示的是一样多的，因此需要先将之前的全部进行复制，然后再增加当前砝码的贡献即可。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1E5+10;
int a[110];
bool dp[110][N];
int vis[N];
int sum,cnt;
int main(){
    int n;cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];sum+=a[i];
        dp[i][a[i]]=1;
        if(!vis[a[i]]){
            vis[a[i]]=1;cnt++;
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=sum;j++){
            if(!dp[i][j])//复制之前可表示重量
            dp[i][j]=dp[i-1][j];
            if(dp[i-1][j+a[i]]||dp[i-1][abs(j-a[i])]){
                //当前砝码的贡献
                if(!vis[j]){
                    vis[j]=1;cnt++;
                } dp[i][j]=1;
            }

        }
    }
    cout<<cnt<<endl;
    return 0;
}

杨辉三角

参考博客
暴力肯定是过不了的啦。
关于杨辉三角我只知道某个数等于其肩上两个数字之和…其他一概不知道，然后从百度学了以下性质：

每个数等于它上方两数之和。
每行数字左右对称，由1开始逐渐变大。
第n行的数字有n项。
前n行共[(1+n)n]/2 个数。
第n行的m个数可表示为 C(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。
第n行的第m个数和第n-m+1个数相等，为组合数性质之一。
每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和，这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
(a+b)ⁿ的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
斜线上数字的和等于其向左（从左上方到右下方的斜线）或向右拐弯（从右上方到左下方的斜线），拐角上的数字。1+1=2，1+1+1=3，1+1+1+1=4，1+2=3，1+2+3=6，1+2+3+4=10，1+3=4，1+3+6=10，1+4=5。
将各行数字左对齐，其右上到左下对角线数字的和等于斐波那契数列的数字。1，1，1+1=2，2+1=3，1+3+1=5，3+4+1=8，1+6+5+1=13，4+10+6+1=21，1+10+15+7+1=34，5+20+21+8+1=55。

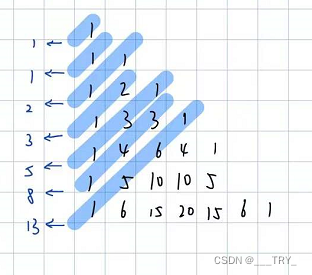
因为左右对称，所以一个数只会在左边第一次出现，右边可以直接咔嚓掉不管了；因为每行左端都是递增的，查找的时候采用二分;找到某个数字的行列位置就可以通过该式子知道它是第几个数字。从第 $1$ 行到第 $33 行$ ，分别对每行进行二分查找。
但是只有20分…

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n;
ll C(int a,int b){
    ll ans=1;
    for(int i=a,j=1;j<=b;i--,j++){
        ans=ans*i/j;
    }
    return ans;
}
int main(){
    cin>>n;
    if(n==1){
        cout<<1<<endl;
        return 0;
    }
    for(int i=1;i<=33;i++){//枚举每一行 i表示i+1行
        int l=1,r=(i+1)/2;//每一行二分答案
        int mid=(l+r)>>1;
        int ans=mid;
        while(l<=r){
            mid=(l+r)>>1;
            if(C(i,mid)==n){
                cout<<(1+i)*i/2+ans+1<<endl;
                return 0;
            }
            if(C(i,mid)<n){
                l=mid+1;
            else r=mid-1;
        }
    }
    return 0;
}

每行枚举并不能获得答案，虽然到了第33行的中间值已经达到 $1 e 9$ ,但是第33行下面仍然存在小于 $1 e 9$ 的数字，因此按行枚举是不全面的，怎么枚举到所有的数字呢？按斜行看，因为每个数都等于其肩上两个数字之和，且杨辉三角均为正数，因此每个从右上角到左下角的斜行都是从上往下递增的，我们知道第 $33$ 行中间数字达到 $1 e 9$ ，其左下角整个斜行都大于该数。因此可以枚举每个斜行，同时二分每个斜行。

设 $k + 1$ 表示当前枚举的斜行，每个斜行都是有序的，最小值是中间数，根据从百度搜刮来的性质5，我们可以知道作为最小值的中间数为 $C_{2×k}^k$ 。而最大值是无穷大，我们可以用一下简单的放缩法，最大值一定大于等于 $n$ ，因此大于等于 $C_k^n$ 。由性质5我们知道，二分时第 $k$ 斜行的第 $i + 1$ 横行的数表示为 $C^k_i$ 。

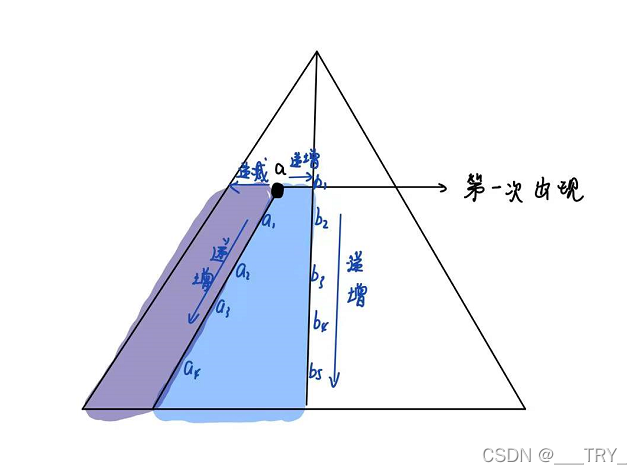
最后还有一个问题，枚举行的时候要从后向前枚举,如图假设 $a$ 在该位置第一次出现，图中 $a_i,b_i$ 均小于 $a$ ,蓝色区域必然不再有 $a$ 出现了，但是在紫色区域 $a$ 仍然可能出现，如果枚举斜行从左上到右下，就会导致在紫色区域中的 $a$ 的位置先被枚举到，但它们的位置在全部排成一列后明显是更靠后的。
在这里插入图片描述

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n;
ll C(int a,int b){
    ll ans=1;
    for(int i=a,j=1;j<=b;i--,j++){
        ans=ans*i/j;
        if(ans>n)return ans;
    }
    return ans;
}
int main(){
    cin>>n;
    for(int k=16;;k--)//枚举斜行
    {
        int l=2*k,r=max(l,n);
        int mid=(l+r)>>1,ans=mid;
        while(l<=r){
            mid=(l+r)>>1;
            if(C(mid,k)>=n){
                r=mid-1;
                ans=mid;
            }
            else l=mid+1;
        }
        if(C(ans,k)==n){
            cout<<1LL*(ans+1)*ans/2+k+1<<endl;
            return 0;
        }
    }
    return 0;
}

括号序列

参考题解
思路实在是太难了，有几个很难思考到的点子：

用dp来解题。（求的是方案数，一般dp或者dfs，dfs复杂度会巨高，数据有5000…）状态的设计是： $d p [i] [j]$ 表示到第 $i$ 个位置左括号比右括号多了 $j$ 个的情况数。
我们可以尝试思考这个状态的合理性：先考虑最终的目标：左右括号数量相同，并且位置不能错乱。第一点比较好保证，第二点需要保证在每个位置左括号个数总是不小于右括号个数。因此最终的状态和下标以及左括号大于右括号个数相关，即在第 $n$ 个下标处，左括号大于右括号个数为 $1$ ,到这里状态的设计就自然而然了。要考虑 $d p$ 状态的设计，可以尝试从最后目标状态出发，由最后的状态如何来设计状态。（但是像我都看不出用dp解大概是没救了哟）
添加左括号和右括号是独立的，互不干扰。也就是说我们可以将添加左括号的总情况数量和添加右括号的总情况数量分别计算出来，最后再将两个情况数相乘以得到最终的结果。

状态设计； dp[i][j]表示在第i个位置左括号比右括号多j个时添加的最少括号数量。
状态转移： 我们只添加左括号，且只在右括号前面增加左括号。

当前位置i为左括号时，不添加左括号，直接从dp[i-1][j-1]而来，即相对于i-1的位置多了一个括号，因此第二维为j-1,因为左括号比右括号多的个数应该相对现阶段更少。
当前位置i为右括号时，则在它前面添加左括号，最少添加0个，最多添加n个，枚举0到n个左括号：当添加0个左括号时，种类数为f[i-1][j+1]，当添加1个左括号，种类数为f[i-1][j]，当添加2个左括号，种类数为f[i-1][j-1]…直到种类数为f[i-1][0],即左括号和右括号相等，就不能再从某个状态添加左括号以获得当前状态了，因为左括号不少于右括号，不存在左括号少于右括号的状态。故 $dp[i[j]=\sum\limits_{k=0}\limits^{k=j+1}dp[i-1][k]$
但是这样计算时间复杂度为O(n³)?，发现
$dp[i[j-1]=\sum\limits_{k=0}\limits^{k=j}dp[i-1][k]$
因此可用O(1)计算出 $d p [i] [j] = d p [i] [j ? 1] + d p [i ? 1] [j + 1]$

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e3+10,mod=1e9+7;
string str;
int n;
ll dp[N][N];
ll cal(){
    memset(dp,0,sizeof dp);
    dp[0][0]=1;
    for(int i=1;i<=n;i++){
        if(str[i-1]=='(')//不添加括号 直接转移
            for(int j=1;j<=n;j++)
                dp[i][j]=dp[i-1][j-1];
        else{
            //初始状态更新 dp[i][0]表示左右括号相同的状态 枚举添加左括号个数为0和1个。
            dp[i][0]=(dp[i-1][1]+dp[i-1][0])%mod;
            for(int j=1;j<=n;j++)
                dp[i][j]=(dp[i-1][j+1]+dp[i][j-1])%mod;
        }
    }
    for(int i=0;i<=n;i++){
        if(dp[n][i])return dp[n][i];
    }
    return 0;
}
int main(){
    cin>>str;
    n=str.length();
    ll l=cal();
    reverse(str.begin(),str.end());
    for(int i=0;i<n;i++){
        if(str[i]=='(')str[i]=')';
        else  str[i]='(';
    }
    ll r=cal();
    cout<<(l*r)%mod<<endl;
    return 0;
}