[数据结构与算法]Leetcode 6003 移除所有载有违禁货物车厢所需的最少时间

前言：与这道极为类似的题目我曾两度遇到，第一次是在比赛中，我没做出来。正好，力扣本周的周赛题又出了这道，便想写个题解。

6003. 移除所有载有违禁货物车厢所需的最少时间

给你一个下标从 0 开始的二进制字符串 s ，表示一个列车车厢序列。s[i] = '0' 表示第 i 节车厢 不 含违禁货物，而 s[i] = '1' 表示第 i 节车厢含违禁货物。

作为列车长，你需要清理掉所有载有违禁货物的车厢。你可以不限次数执行下述三种操作中的任意一个：

1. 从列车 左 端移除一节车厢（即移除 s[0]），用去 1 单位时间。
2. 从列车 右 端移除一节车厢（即移除 s[s.length - 1]），用去 1 单位时间。
3. 从列车车厢序列的 任意位置 移除一节车厢，用去 2 单位时间。

返回移除所有载有违禁货物车厢所需要的 最少 单位时间数。

注意，空的列车车厢序列视为没有车厢含违禁货物。

动态规划题解：

大致思路：动态规划的关键基础是最优子结构的寻找，这题两侧是对称的为我们找寻子结构增添了些许困难，但观察后可以发现如果条件1，2任意删去一者，子结构就明朗起来。而答案一定同时具有两种子结构（即存在一个分界点，该点左处条件1和3适用，而右侧则适用2和3），于是便有了下述的解法。

?

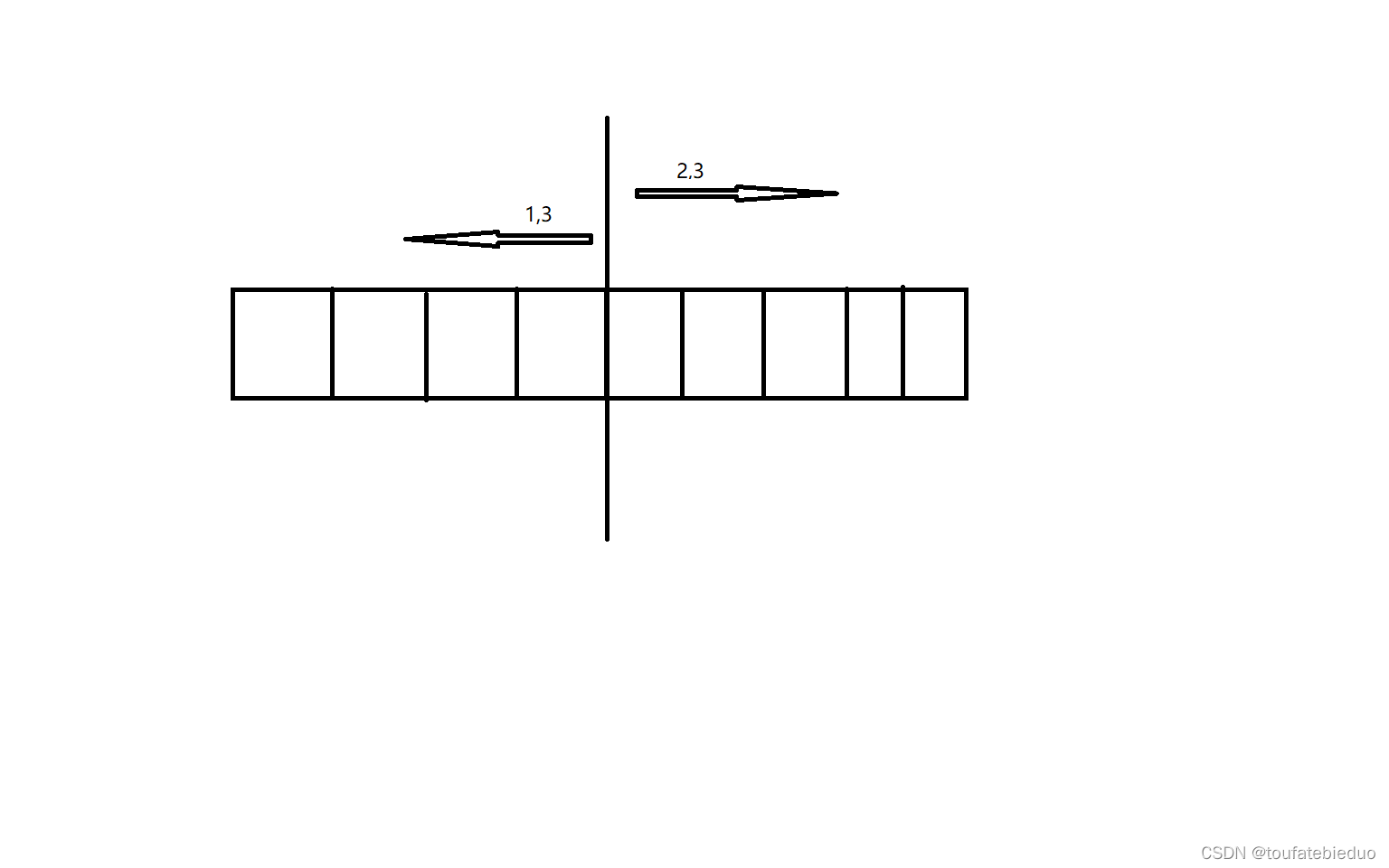
对于左侧，数组front[ i ]为将第 i 个车厢及其之前的违禁货物去除所花时间。如果第 i 个车厢为无需移除（为0），则；若需要移除（为1），则可以使用规则3直接移除，或将第 i 位和其右侧完全移除，。右侧对称。综上，有状态转移方程：

?

构建完数组后(第一个元素需要注意)，枚举断点，得到时间最短的即可 ：

?

?最后愉快地编程实现即可~~~

class Solution {
public:
    int front[200005],back[200005];
    int minimumTime(string s) {
        int len=s.length();
        //动态规划得到front数组
        front[0]=s[0]=='0'?0:1;
        for(int i=1;i<len;i++){
            if(s[i]=='0'){
                front[i]=front[i-1];
            }else{
                front[i]=min(front[i-1]+2,i+1);
            }
        }
        //动态规划得到back数组
        back[len-1]=s[len-1]=='0'?0:1;
        for(int i=len-2;i>=0;i--){
            if(s[i]=='0'){
                back[i]=back[i+1];
            }else{
                back[i]=min(back[i+1]+2,len-i);
            }
        }
        //枚举断点
        int ans=1000000;//充分大即可
        for(int i=0;i<len;i++){
            ans=min(ans,front[i]+back[i+1]);
        }
        return ans;
    }
};