51. N 皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
输入:n = 4
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
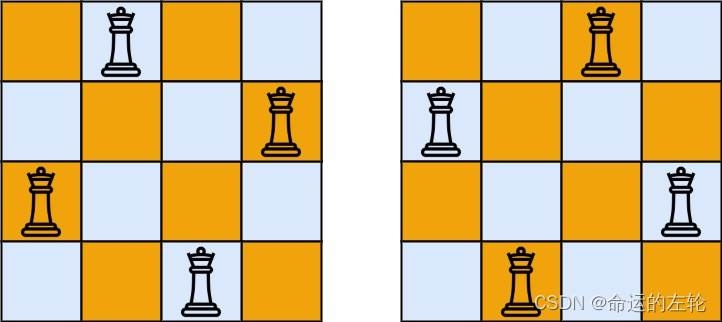
示例 2:
输入:n = 1
输出:[["Q"]]
提示:
1 <= n <= 9
分析
- 著名的n皇后问题,抽象为树的结构,用回溯法做。

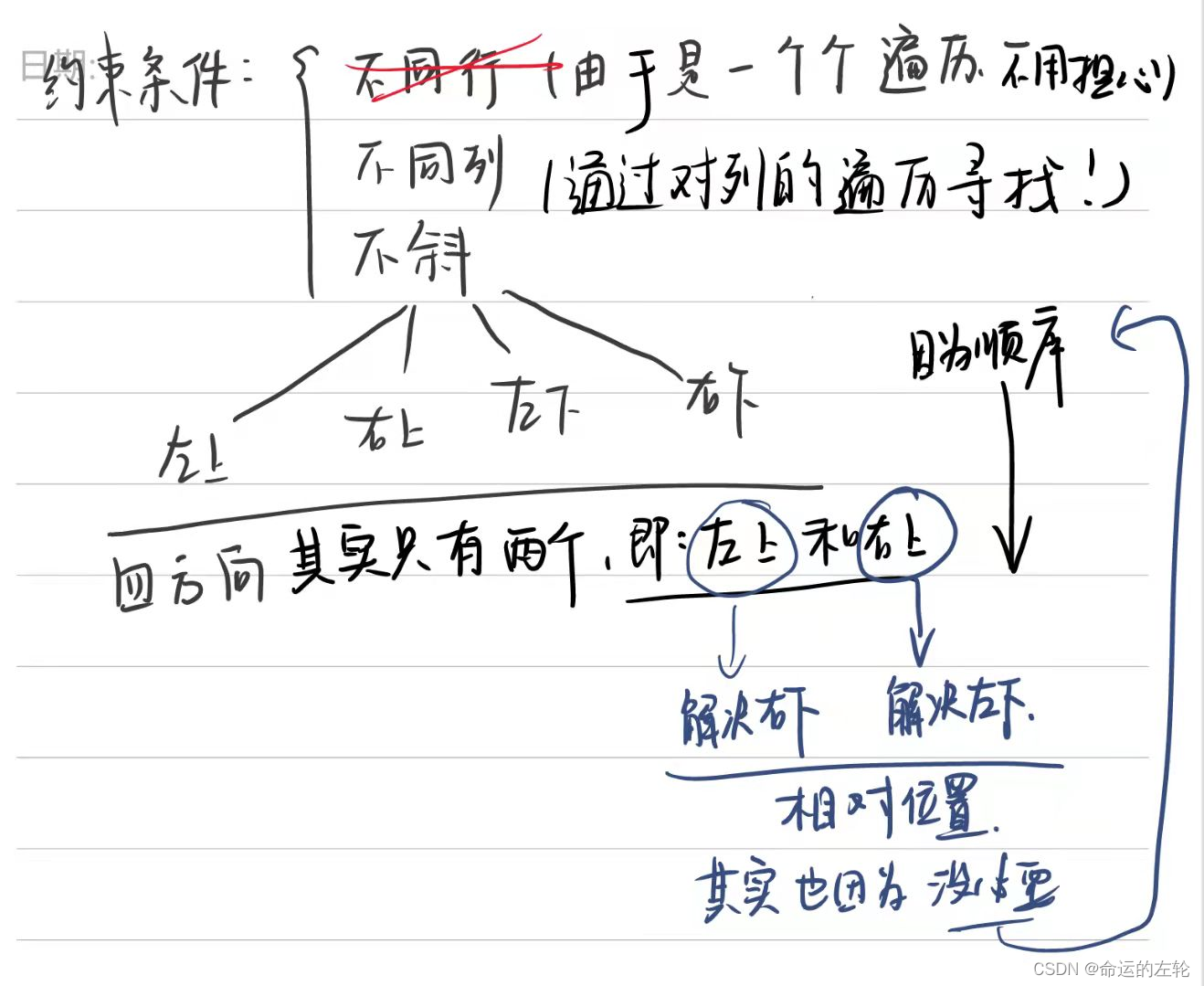
- 检查是否同行同列同斜线比较简单,这里看代码就可以理解。
- 如果没有同行同列同斜线,就递归行加一,继续找,代码后面记得回溯。
- 终止条件就是能到最后一行加一,添加到结果里面
- 棋盘问题就是一个二维的问题,遍历列增加行,从而达到遍历所有棋盘格的目的。
代码
class Solution:
def solveNQueens(self, n: int) -> List[List[str]]:
checkboard = [['.']*n for _ in range(n)] # 创建一个全为.的二维棋盘
res = []
def isfight(row,col): # 还没落子前的检查
# 保证不同列
for i in range(n):
if checkboard[i][col] == 'Q':
return False
# i,j分别记录落子未知的行列
i = row
j = col
# 搜索左上
while i > 0 and j >0:
if checkboard[i-1][j-1] == 'Q':
return False
i-=1
j-=1
i = row
j = col
# 搜索右上
while i > 0 and j < n-1:
if checkboard[i-1][j+1] == 'Q':
return False
i-=1
j+=1
return True
def backtrack(row):
if row == n: # 即最后一行弄好
res2 = []
res.append(res2)
for i in checkboard:
res2.append("".join(i))
for col in range(n):
if not isfight(row,col):
continue
checkboard[row][col] = 'Q'
backtrack(row+1)
checkboard[row][col] = '.'
backtrack(0)
return res
通过截图
37. 解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。

示例:
输入:board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出:[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字或者 '.'
题目数据 保证 输入数独仅有一个解
分析
- 个人感觉数独问题比皇后难得多。因为皇后每一格不是有就是没有,而数独问题每一格有九种可能。所以递归的深度一般比皇后更高。
- 首先还是判断同行,同列,同九宫格是否有重复元素。我们准备填充的元素遍历同行同列看看有没有相同元素即可。主要是九宫格的遍历,我们必须找到九宫格一个可以确定的元素,最好写代码的其实是左上角那个元素。
- 比如第一个九宫格左上角位置为(0,0),第一个九宫格的范围为0-2,行列都是如此。所以0整除3等于0,1整除3也等于0,2整除3依然为0。大家可以尝试第二个,第三个九宫格是否满足此规律,由于这个规律比较好找,这里不多加赘述。
- 遍历所有格,找到
‘.’(即找到没有填充的位置),然后再依次填充,如果同行同列同九宫格元素没有重复元素,填入,题目要求是字符类型,就转为字符类型。 - 递归的时候要
return True,判定为一条可行路径。1到9找不到填充的数字就返回False,能遍历到九宫格结束也返回True
代码
class Solution:
def solveSudoku(self, board: List[List[str]]) -> None:
def isfight(row,col,val):
# 检测行
for i in range(9):
if board[i][col] == val:
return False
# 检测列
for i in range(9):
if board[row][i] == val:
return False
# 检测九方格
row_start = row//3*3
col_start = col//3*3
for i in range(row_start,row_start+3):
for j in range(col_start,col_start+3):
if board[i][j] == val:
return False
return True
def backtrack(row,col):
for i in range(9):
for j in range(9):
if board[i][j] != '.':
continue
for z in range(1,10): # 填充范围
if isfight(i,j,str(z)):
board[i][j] = str(z)
if(backtrack(i,j)):
return True
board[i][j] = '.'
return False
return True
backtrack(0,0)
通过截图
如有错误,敬请指正,欢迎交流,谢谢?(・ω・)ノ