[数据结构与算法]「LeetCode」第71场双周赛 题解

碎碎念

由于各种事情比赛开始后十分钟才开始做题，状态也心不在焉
由于最后急着刷排名，心态很急，思路没有整理就上手敲代码
结果只AC了前三题，最后一题实在没心态了

5984. 拆分数位后四位数字的最小和

解题思路

很明显的贪心，对于四位数，用一个长度为4的数组a保存各位的数值
题目要求构成的两个两位数之和最小；
首先对数组a从小到大排序，
两位小的一定分别是两个数的十位，而两位大的一定分别是两个数的个位

代码

class Solution {
public:
    int a[4];
    int minimumSum(int num) {
        a[0] = num / 1000;
        a[1] = num / 100 % 10;
        a[2] = num % 100 / 10;
        a[3] = num % 10;
        
        sort(a, a + 4);
        
        return (a[0] * 10 + a[2]) + (a[1] * 10 + a[3]);
    }
};

5985. 根据给定数字划分数组

解题思路

额外开了两个vector，扫描一遍，分别将小于p的数放入a
对等于p的计数
对大于p的数放入b
最后将所有元素放入a;

代码

class Solution {
public:
    vector<int>a, b;
    int cnt = 0;
    vector<int> pivotArray(vector<int>& nums, int pivot) {
        for (int i = 0; i < nums.size(); i++) {
            if (nums[i] < pivot)  a.push_back(nums[i]);
            else if (pivot == nums[i]) cnt++;
            else b.push_back(nums[i]);
        }

        for (int i = 0; i < cnt; i++) a.push_back(pivot);
        for (auto& x : b)   a.push_back(x);
        return a;
    }
};

5986. 设置时间的最少代价

解题思路

分钟数和秒数的范围都是0~99；
我们可以对分钟数从0~99枚举，秒数自然可以由公式int j = targetSeconds - i * 60得出
如果算出来的秒数不在正常范围内，则进行下一次循环，否则去除前导0后开始比大小
而反过来对秒数从0~99枚举，并不能算出分钟数

TIPS：对于此题，我们要尽量避免的前导0的计算，因为前导0只会额外增加cost

代码

class Solution {
int ans = 1e9;
int c[4];
public:
    int minCostSetTime(int startAt, int moveCost, int pushCost, int targetSeconds) {
        for (int i = 0; i <= 99; i++) {
            int j = targetSeconds - i * 60;
            if (j < 0 || j > 99)    continue;
            c[0] = i / 10; c[1] = i % 10;
            c[2] = j / 10; c[3] = j % 10;

            bool flag = false;
            int res = 0, d = startAt;
            for (int k = 0; k < 4; k++) {
                if (c[k])  flag = true;  // 只有不是前导0时，才开始操作
                if (flag) {
                    if (c[k] != d)
                        res += moveCost, d = c[k];
                    res += pushCost;  
                }
            }
            ans = min(ans, res);
        }
        return ans;
    }
};

5987. 删除元素后和的最小差值

题目描述

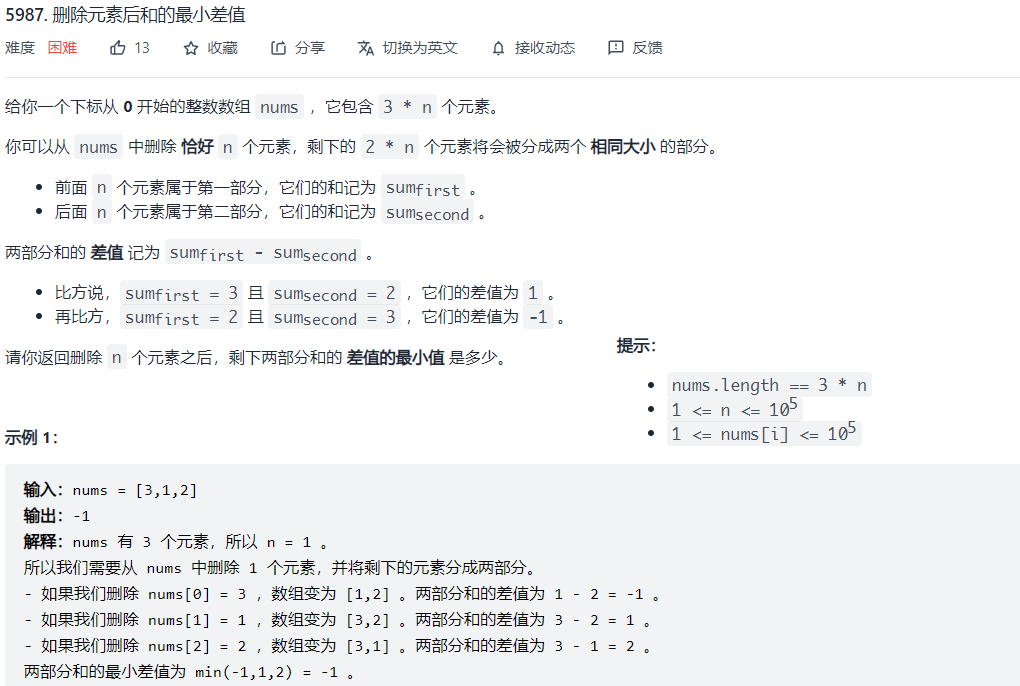
解题思路

可以参考这个题解
简而言之，由于我们最后只需要2 * n 个元素，并分为两半，
题目要求前一半减去后一半的差值最小 => 要求前一半最小，后一半最大
因此我们可以用一个小根堆求出前缀最小和，用一个大根堆求出后缀最大和

当小根堆/大根堆的数量到达了n之后，
对于下一个num[i]可以先加入堆，然后弹出堆顶，并更新某个区间的前缀最小和/后缀最大和

代码

class Solution {
public:
    long long minimumDifference(vector<int>& nums) {
        int m = nums.size(), n = m / 3;
        priority_queue<int, vector<int>, greater<int>> minQ;
        long long sum = 0;

        for (int i = m - n; i < m; i++) {
            minQ.push(nums[i]);
            sum += nums[i];
        }

        vector<long long> sufMax(m - n + 1);
        sufMax[m - n] = sum;
        for (int i = m - n - 1; i >= n; i--) {
            minQ.push(nums[i]);
            sum += nums[i] - minQ.top();
            minQ.pop();
            sufMax[i] = sum;  // 更新后缀最大值
        }

        priority_queue<int> maxQ;
        long long preMin = 0;
        for (int i = 0; i < n; i++) {
            maxQ.push(nums[i]);
            preMin += nums[i];
        }

        long long ans = preMin - sufMax[n]; 
        for (int i = n; i < m - n; i++) {
            maxQ.push(nums[i]);  // 先加入堆
            preMin += nums[i] - maxQ.top();  
            maxQ.pop();  // 将最大值弹出
            ans = min(ans, preMin - sufMax[i + 1]);
        }
        return ans;
    }
};