题目:数字在升序数组中出现的次数
描述:给定一个长度为 n 的非降序数组和一个非负数整数 k ,要求统计 k 在数组中出现的次数
要求:数据范围:0≤n≤1000,0≤k≤100,数组中每个元素的值满足0≤val≤100
要求:空间复杂度O(1),时间复杂度O(logn)
1.二分查找
二分查找是一种在有序数组中运用到的快速查找的算法,也称“折半查找(Binary Search)”。时间复杂度为O(logn),相对遍历查找,是一种较为优秀的算法。基本原理是通过将一个有序数组的中间值与目标值进行对比,若恰好等于中间值则返回该值;若目标值大于中间值,则压缩左边界,逼近目标值;若目标值小于中间值,则压缩右边界,逼近目标值。代码示例如下:(假设数组升序排列)
#include<stdio.h>
int find_t(int* a, int key, int sz)
{
int left = 0, right = sz - 1;
int mid = 0;
while (left <=right)//循环条件是左边小于等于右边,当左边大于右边,不用再循环;
{
mid = (right - left) / 2 + left;//找到中间值(此做法是为了避免溢出)
if (a[mid] < key)//当要找到的key在中间值的右边时
{
left = mid+1;//左边界向前进一位,压缩寻找范围
}
else if (a[mid] > key)//当要找到的key在中间值的左边时
{
right = mid-1;//右边界向后退一位,压缩寻找范围
}
else
return mid;//当key刚好等于中间值,返回该值
}
return -1;//遍历整个数组后,都没有找到合适值,说明该数组中没有要寻找的key值,返回-1;
}
int main()
{
int k = 0;
int arr[] = { 3,7,8,16,25,34,43,52,61,70 };
while (1)
{
scanf("%d", &k);
int sz = sizeof(arr) / sizeof(arr[0]);
if (find_t(arr, k, sz) != -1)
printf("exist the number is:%d\n", find_t(arr, k, sz));
else
printf("no exist!\n");
}
return 0;
}
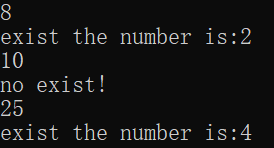
程序运行结果如下:
2.?计算数字在升序数组中出现的次数
一、方法一
暴力遍历,无视顺序
该方法无论有序无序,均适用。直接从第一个数字开始,遍历整个数组,一旦遇见目标值就+1,但该方法相对二分法较为费时,代码如下:
int GetNumberOfK(int* data, int dataLen, int k )
{
int count=0;//定义一个count为0;
for(int i=0;i<dataLen;i++)
{
if(data[i]==k)//遇到与目标值k相同的就+1;
count++;
}
return count;//返回该值
}二、方法二
二分法查找
使用二分法查找,因为查找的数组有序,所以目标值如果有多个,肯定是连在一起,我们可以通过二分查找,找到该一串连续数字的左右边界,例如:
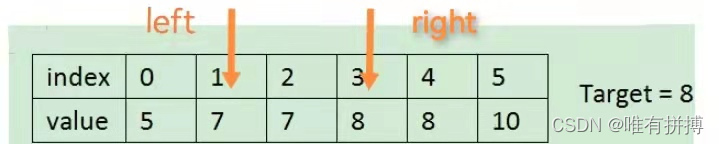
上述代码中,如果目标值为7,则左边界就是该段数组中的第一个7,右边界为该段数组中的最后一个7再加一位,即对应上图中的第一个8,用8的下标,减去第一个7的下标即为该数组中7的个数,即right-left.
所以,需要进行两次二分查找,分别找出左右边界,代码如下:
int GetNumberOfK(int* data, int dataLen, int k )
{
int l=0,r=dataLen,left=0,right=0;
while(l<r)
{
//确定左界
int mid=(r-l)/2+l;//计算中间值
if(data[mid]<k)
l=mid+1;
else
r=mid;
}
left=l;
//重新赋值,再次进行一次二分查找,确定右界
l=0;r=dataLen;
while(l<r)
{
int mid=(r-l)/2+l;//计算中间值
if(data[mid]<=k)
l=mid+1;
else
r=mid;
}
right=r;
return right-left;//个数为右边界减去左边界
}这里注意:
二分查找,可以用于查找边界值或者具体某一个目标值,第一部分举的二分法示例时找具体某一个值,而该题是寻找边界值,要注意在寻找边界值时,while中的判断部分是left<right,左右边界的每一次循环后的值要根据具体情况判断是=mid+(-)1,还是=mid;