密码学入门(5):单向散列函数
在开始之前,我们先假设一个场景:我们现在想下载一个ubuntu的镜像文件,如何确保我们下载的文件是和原始文件一模一样的呢?下载的过程中可能会因为网络原因,或者其他可能的原因,导致下载的镜像文件不完整,即使是 1 1 1个bit的不同。
其实,我们可能已经接触过单向散列函数了。在下载镜像文件时,在下载页面可能会看到md5、sha256之类的字眼,后面跟了一堆数字和字母的序列。例如:
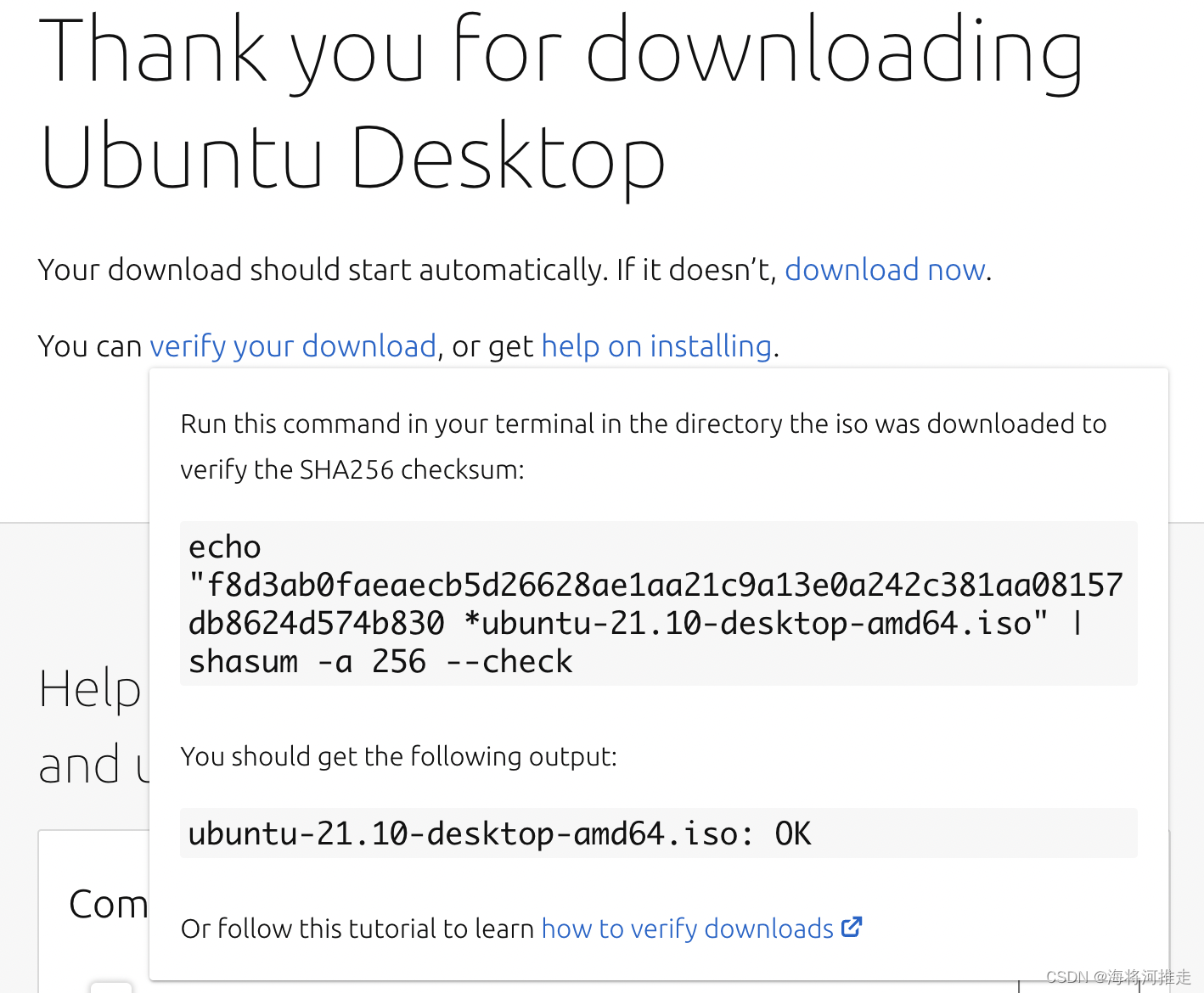
这里的f8d3ab0faeaecb5d26628ae1aa21c9a13e0a242c381aa08157db8624d574b830就是单向散列函数生成的散列值。通过计算下载的镜像文件的散列值,再和这串散列值对比,就可以验证文件是否完整了。这是单向散列函数的一个应用。
什么是单向散列函数
单向散列函数(one-way hash function)有一个输入和一个输出,其中输入称为消息(message),输出称为散列值(hash value)。它可以根据消息的内容计算出散列值,而散列值可以用来检查消息的完整性。
单向散列函数的相关术语有很多变体,例如:
- 单向散列函数也称为消息摘要函数(message digest function)、哈希函数或杂凑函数。
- 输入单向散列函数的消息也称为原像(pre-image)。
- 单向散列函数输出的散列值也称为消息摘要(message digest)或者指纹(fingerprint)。
- 完整性也称为一致性。
单向散列函数除了上面说的可以用来验证文件的完整性,还可以用于构造消息认证码、数字签名、构造伪随机数生成器等。
单向散列函数无法解决的问题:单向散列函数能够辨别出“篡改”,但无法辨别出“伪装”。即只能保证消息的完整性,不能对消息进行认证。用于认证的技术包括消息认证码和数字签名,我们将在之后讨论。
单向散列函数的性质
- 根据任意长度的消息计算出固定长度的散列值:无论输入多长的消息( 1 1 1字节、 1 1 1MB、 1 1 1GB、 1 1 1TB或更大),输出的散列值都是固定长度(例如sha256是 256 256 256bit)。
- 能够快速计算出散列值。
- 具备单向性:根据消息计算散列值很容易,但根据散列值计算消息很困难。
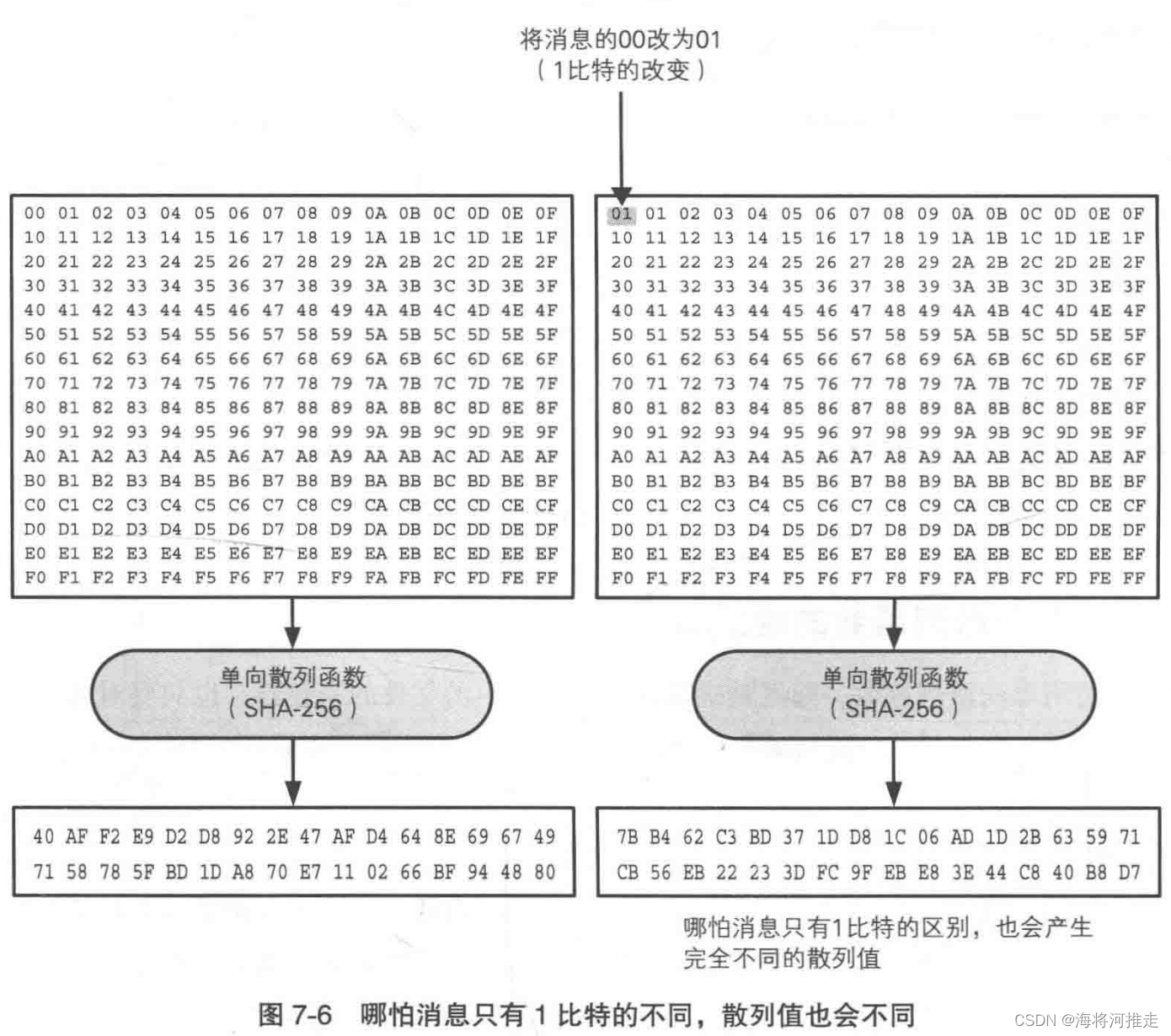
- 消息不同散列值也不同:消息中哪怕只有 1 1 1比特的改变,也必须有很高的概率产生不同的散列值。
- 抗碰撞性:两个不同的消息产生同一个散列值的情况称为碰撞(collision)。难以发现碰撞的性质称为抗碰撞性(collision resistance)。
- 雪崩效应:当输入发生最微小的改变(例如,反转一个二进制位)时,也会导致输出的不可区分性改变(输出中每个二进制位有50%的概率发生反转):
MD4、MD5
- MD4是由Rivest于1990年设计的单向散列函数,能够产生 128 128 128比特的散列值。现在已经不安全了。
- MD5是由Rivest于1991年设计的单向散列函数,能够产生 128 128 128比特的散列值。现在也不安全了。
- MD4和MD5中的MD是消息摘要(Message Digest)的缩写。
SHA家族
- SHA-1于1995年发布,是由NIST(National Institute of Standards and Technology)设计的一种能产生 160 160 160比特的散列值的单向散列函数,是MD5的后继者。现在已经被攻破了。
- SHA-2于2001年发布,包括SHA-256、SHA-384、SHA-512等,散列值长度分别为 256 256 256比特、 384 384 384比特和 512 512 512比特。这些单向散列函数合起来统称SHA-2。SHA-2目前没有出现明显的弱点。
- SHA-3与2015年发布,由于对MD5成功的破解,以及对SHA-0和SHA-1出现理论上破解的方法,NIST感觉需要一个与之前算法不同的,可替换的加密散列算法,也就是现在的SHA-3。SHA-3和AES一样采用公开竞争的方式进行标准化,最后一个名叫Keccak的算法胜出,最终成为了SHA-3。
暴力破解
假设有一条消息,经过SHA-512计算后的到散列值,由于散列值长度为 512 512 512比特,根据鸽巢原理,我们最多只需要尝试 2 512 2^{512} 2512次就能找到一条和原消息不同但散列值相同的消息,但如此多的尝试次数在现实中是不可能完成的。
由于尝试次数纯粹是由散列值的长度决定的,因此散列值长度越长,抵御暴力破解的能力也就越强。
生日攻击
生日攻击(birthday attack)与暴力破解的不同之处在于,生日攻击不是寻找生成特定散列值的消息,而是要找到散列值相同的两条消息,其中散列值可以是任意值。
假设一个班上有 30 30 30名学生,问至少一名学生和另外任意一名学生有着相同生日的概率是多少?
从直觉上看概率貌似很小,但实际上概率大约为 70.63 % 70.63\% 70.63%。
为了计算这个概率,我们可以先计算每个人生日不一样的概率 P ′ P' P′,然后用 1 ? P ′ 1 - P' 1?P′就能得到“至少一名学生和另外任意一名学生有着相同生日的概率”:
P ′ = 365 365 × 364 365 × 363 365 × . . . ? × 365 ? 30 + 1 365 = 365 × 364 × 363 × . . . ? × ( 365 ? 30 + 1 ) 35 6 30 ≈ 29.37 % P = 1 ? P ′ ≈ 70.63 % \begin{aligned} P' &= \frac {365} {365} \times \frac {364} {365} \times \frac {363} {365} \times ...\, \times \frac {365 - 30 + 1} {365} \\ &= \frac {365 \times 364 \times 363 \times ...\, \times (365 - 30 + 1)} {356^{30}} \\ &\approx 29.37\% \\ P &= 1 - P'\approx 70.63\% \end{aligned} P′P?=365365?×365364?×365363?×...×365365?30+1?=35630365×364×363×...×(365?30+1)?≈29.37%=1?P′≈70.63%?
实际上,假设一年有 Y Y Y天,那么 N N N人的集合中,至少有两个人生日一样的概率大于 50 % 50\% 50%, N N N至少为 Y \sqrt Y Y?,即 Y 1 2 Y^\frac 1 2 Y21?。
对于 512 512 512比特的散列值来说, Y Y Y为 2 512 2^{512} 2512,因此对同一单向散列函数进行生日攻击需要的次数为 2 512 = 2 256 \sqrt {2^{512}} = 2^{256} 2512?=2256次,比暴力破解所需的攻击次数少得多。
应该使用那种单向散列函数
- MD5是不安全的,不应该使用。
- SHA-1除了用于对过去生成的散列值进行校验之外,不应被用于新的用途。
- SHA-2有效应对了针对SHA-1的攻击方法,因此是安全的,可以使用。
- SHA-3是安全的,可以使用。
- 和对成密码算法一样,我们不应该使用任何自制算法。