一、贪心算法思想
??贪心算法的思想就是将问题分解为一个一个的子问题,对每个子问题都去取在子问题条件下的最优解,然后把这些解组合到一起即为贪心算法的解。
??从贪心算法思想的描述就能看出,这种算法很难保证自己的解就是问题的最优解,因为最优解对应的子结构可能不都是最优的,这时便无法使用贪心算法。
??由于这个问题,贪心算法的应用场景相对较少,这里把目前本人见过的贪心算法的使用场景总结如下,以供参考和复习。
二、买卖股票的最佳时机II
链接:买卖股票的最佳时机II
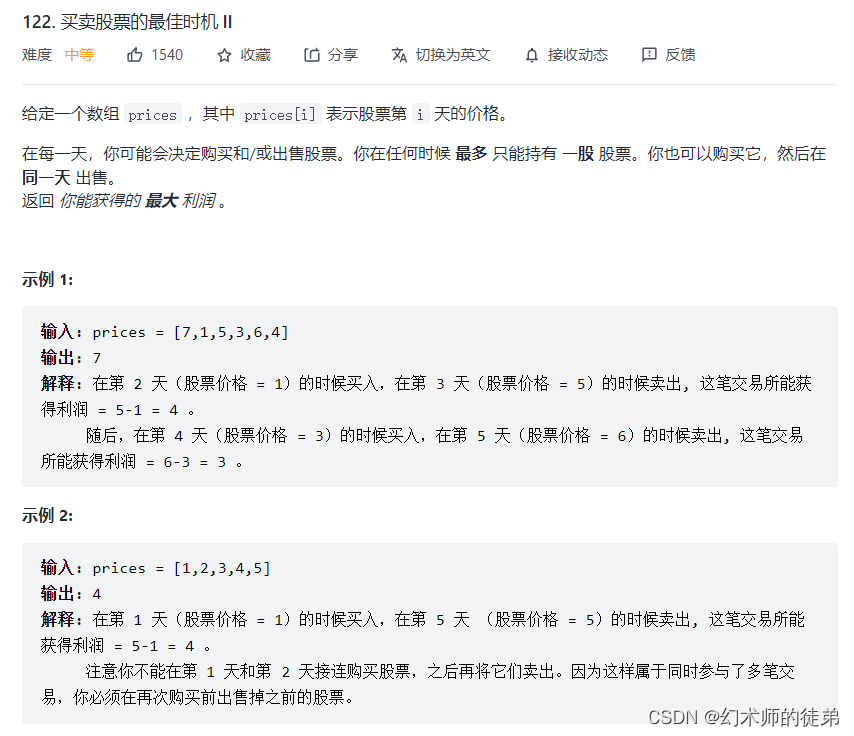
??本题之所以可以使用贪心算法,是因为本题没有限制股票交易次数,对于连续上涨的股票,贪心策略下,我们可以在最低点买入,在最高点卖出。
??由于没有限制股票交易次数,这个策略可以转化为如果明天的股票比今天高,那么就买入今天的股票,在明天卖出;由于不限制交易次数且没有手续费,对于连续上涨情况,就可以等价的转化为在第一天买入,在第二天卖出,然后又在第二天买入,在第三天卖出…
??对于下跌时,则不进行操作。
代码:
class Solution {
public:
int maxProfit(vector<int>& prices)
{
int ret = 0;
for (int i = 0; i < prices.size() - 1; ++i)
{
if (prices[i + 1] - prices[i] > 0)
ret += prices[i + 1] - prices[i];
}
return ret;
}
};
二、买卖股票的最佳时机含手续费
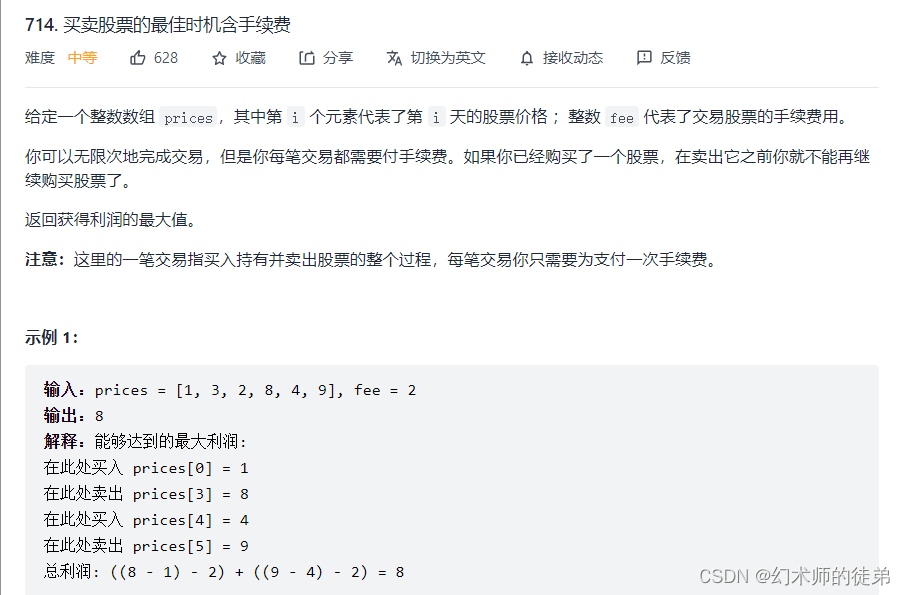
??这里与买卖股票II唯一的不同就是有手续费,那时我们把连续上涨时在最高点套现利用可以当天买入再卖出转化为了,只要明天的价格大于今天 就买入今天并在明天卖出;
??对应到本题 首先 平时的买入价格看做是基础价格加上小费,如果明天卖出能盈利,那么立马卖出,但是为了能在最高点套现,提供一个后悔机制 同时我们再以prices[i + 1]的价格买入股票而不是以price[i + 1] + fee的价格买入,
??这样相当于我可以后悔,如果明天卖出的价格更高,我可以以prices[i]的价格再买入,然后以prices[i + 1]的价格卖出。
??这是什么道理呢?
??比如i~j是连续上涨,i是最低点,j是最高点
??i点买入的价格是prices[i] + fee
??i + 1有盈利 即prices[i + 1] - prices[i] - fee > 0
??卖出 盈利profit = prices[i + 1] - prices[i] - fee
??再以prices[i + 1]买入 然后如果明天价格比今天高:prices[i + 2] - prices[i + 1] > 0
??有盈利空间,卖出,盈利: prices[i + 2] - prices[i + 1] + prices[i + 1] - prices[i] - fee = prices[i + 2] - prices[i + 1] - fee,这就相当于放弃在第i+1天卖出转而选择在第i天卖出
??所以连续上涨时,按照这种操作,利润等于prices[j] - prices[i] - fee,即等价于最低点入场,最高点套现。
class Solution {
public:
int maxProfit(vector<int>& prices, int fee)
{
int buy = prices[0] + fee;
int profit = 0;
for (int i = 0; i < prices.size() - 1; ++i)
{
if (buy > prices[i] + fee)
{
buy = prices[i] + fee;
}
if (prices[i + 1] > buy)
{
profit += prices[i + 1] - buy;
buy = prices[i + 1];
}
}
return profit;
}
};
三、跳跃游戏II
链接:跳跃游戏II
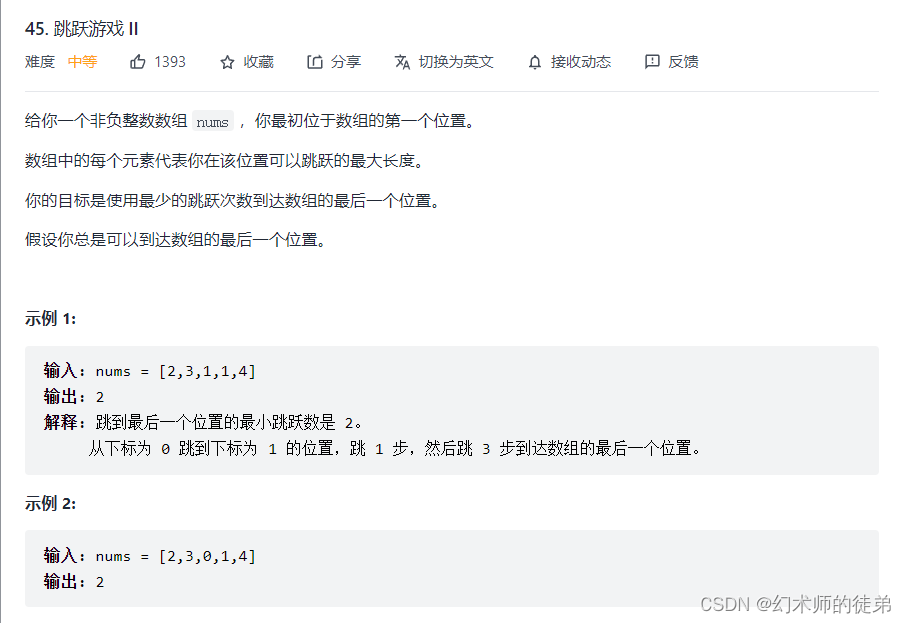
??本题假定了我们总可以到达最右边,让我们用最少的跳跃次数到达最右边,贪心的思想是这样的,维护两个变量prevright和curright,分别表示上次起跳能到达的最右边和本次起跳能到达的最右边,显然两者的初始值都是0.
??怎样才能跳的最少呢?对于这次起跳,我们一直遍历到上次起跳的最右位置时,才选择起跳,起跳次数+1,这时上次起跳的最右位置prevright更新为curright,然后接着往前走;
??如果prevright >= n - 1了,那说明上次起跳就可以到达终点了,于是返回起跳次数就可以了。
??注意,不要遍历最后一个点,因为最后一个点的跳跃距离没有更新的意义且到了最后一个点相当于到了最右边了。
class Solution {
public:
int jump(vector<int>& nums)
{
/*
贪心算法:每次都在上次跳跃能到达的最远位置起跳
每次维护两个变量
一个是上次跳跃可以到达的最右边prevright 初始值为0
一个是这次跳跃可以到达的最右边curright 初始值为0
对每一个还没超过上次跳跃的最远距离的点
更新这次跳跃能到达的最远距离为max(curright, i + nums[i])
当当前点到达了上次跳跃的最右边 即i == prevright
那么说明下个点必须要进行一次跳跃才能到达
跳跃次数ret++
不必遍历最后一个位置 因为最后一个位置就是终点 不要白费一次起跳
*/
int n = nums.size();
int prevright = 0, curright = 0;
int ret = 0;
for (int i = 0; i < n - 1; ++i)
{
curright = max(curright, i + nums[i]);
if (i == prevright)
{
++ret;
/*
到达了上次跳跃的终点了 必须跳跃了
这次跳跃对下一轮来讲 就是上次跳跃
其跳到的最远距离就是curright
*/
prevright = curright;
}
if (prevright >= n - 1)
{
return ret;
}
}
return ret;
}
};
四、零钱找零
假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K
元,至少要用多少张纸币?
??本题的贪心策略是先用贵的纸币找,找的个数为cnt = min(K/v[i], c[i),然后更新K为K - cnt * v[i],然后再用次贵纸币找钱…
代码:
#include <iostream>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
/*
moneymat[i][0] 第i个硬币的面值
moneymat[i][1] 第i个硬币的数量
*/
struct cmp
{
bool operator()(const vector<int>& m1, const vector<int>& m2)
{
return m1[0] > m2[0];
}
};
int maxnum(vector<vector<int>>& moneyMat, int moneytarget)
{
/*首先从大大小按面值排列数组*/
sort(moneyMat.begin(), moneyMat.end(), cmp());
int ret = 0;
for (auto e : moneyMat)
{
/*先取大面额的钱*/
int cnt = moneytarget / e[0];
/*这里的除保证了如果面额大于moneytarget会取到0个该硬币*/
cnt = min(cnt, e[1]);
moneytarget -= cnt * e[0];
ret += cnt;
}
/*如果遍历完所有的硬币还没组成moneytarget,
就返回-1表示无法组成当前面额*/
if (moneytarget != 0)
{
return -1;
}
return ret;
}
int main()
{
vector<vector<int>> a = {{1,5}, {2,6}, {5, 2},
{10, 3},{20, 4},{100, 1}, {50, 3}};
cout << maxnum(a, 123) << endl;
}
五、多机调度问题
某工厂有n个独立的作业,由m台相同的机器进行加工处理。作业i所需的加工时间为ti,任何作业在被处理时不能中断,也不能进行拆分处理。现厂长请你给他写一个程序:算出n个作业由m台机器加工处理的最短时间
??贪心策略:如果n<=m,那么就把每个工作安排到一个空闲的机器上,用时最长的作业即为处理时间;否则先安排时间用时长的工作,然后给空闲机器也安排剩余工作用时最长的工作,直到工作安排结束位置。
??这个策略并不一定是最优的,但是是目前处理多机调度问题较好的策略。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int mymax(const vector<int>& works)
{
int curmax = 0;
for (auto e : works)
{
if (e > curmax)
{
curmax = e;
}
}
return curmax;
}
struct cmp
{
bool operator()(int a, int b)
{
return a > b;
}
};
int findminindex(const vector<int>& machines)
{
int curmin = INT_MAX;
int ret = 0;
int size = machines.size();
for (int i = 0; i < size; ++i)
{
if (machines[i] < curmin)
{
ret = i;
curmin = machines[i];
}
}
return ret;
}
int Getgreedytime(vector<int>& works, vector<int>& machines)
{
int n = machines.size();
int m = works.size();
if (n >= m)
{
return mymax(works);
}
else
{
sort(works.begin(), works.end(), cmp());
int curwaitwork = 0;
/*先依次把用时最长的工作安排上 塞满机器*/
for (int i = 0; i < n; ++i)
{
machines[i] = works[curwaitwork++];
}
while (curwaitwork != m)
{
/*
此时下标最小的机器就是完工空闲的机器
安上
*/
int curoverindex = findminindex(machines);
machines[curoverindex] += works[curwaitwork++];
}
return mymax(machines);
}
}
int main()
{
/*
贪心策略:先安排用时最长的工作
如果机器数大于工作数 这就是最佳策略了
否则就让空闲的机器去走剩余作业中时间最长的工作
*/
int n, m;
cout << "请输入机器数和工作数,以n m的格式输入:" ;
cin >> n >> m;
cout << "请输入每个工作的用时,以a b c d e f这样空格隔开的方式输入" << endl;
vector<int> works(m), machines(n);
for (int i = 0; i < m; ++i)
{
cin >> works[i];
}
cout << "贪心策略的用时为:" << Getgreedytime(works, machines) << endl;
}
六、活动选择
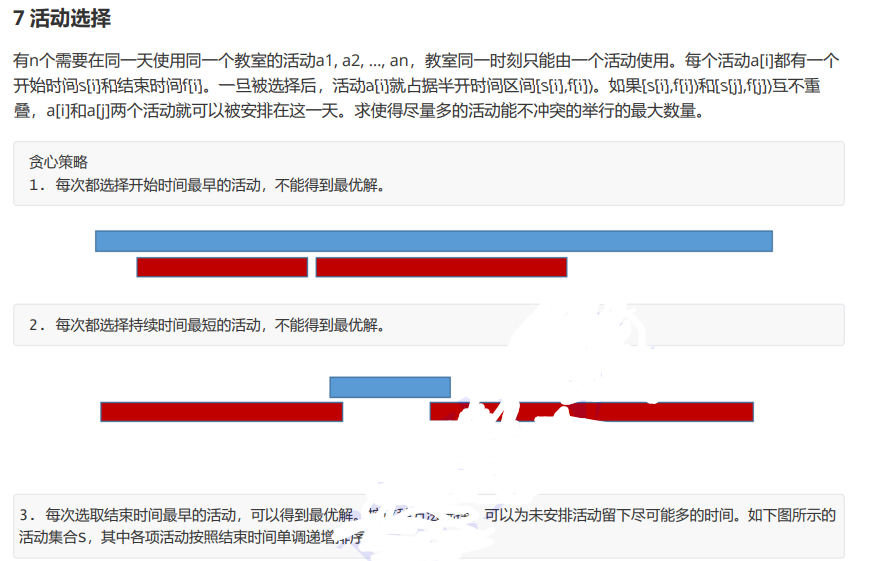
??本题的贪心策略为选择结束时间最早的会议参加,这里的道理是结束时间早的话可选择的会议更多。
代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
/*
events[i][0]:第i个工作的开始时间
events[i][1]:第i个工作的结束时间
先把工作按结束时间排序
贪心策略是
每次都选择可以执行(即events[j][0] >= events[i][1])且最早结束的工作执行
因为这样可以空闲出最多的时间供选择 且选择最早结束的工作暗含了开始时间比较早
*/
struct cmp
{
bool operator()(const vector<int>& a, const vector<int>& b)
{
return a[1] < b[1];
}
};
int getNum(vector<vector<int>>& events)
{
sort(events.begin(), events.end(), cmp());
int ret = 1;
int curwork = 0;
int n = events.size();
for (int j = 1; j < n; ++j)
{
if (events[curwork][1] <= events[j][0])
{
curwork = j;
++ret;
}
}
return ret;
}
int main()
{
vector<vector<int>> events = {{1, 4}, {3, 5}, {0, 6}, {5, 7},
{3, 8}, {5,9}, {6, 10}, {8, 11}, {8, 12}, {2, 13}, {12, 14}};
cout << getNum(events) << endl;
}
七、最多可以参加的会议数目
链接:最多可以参加的会议数目
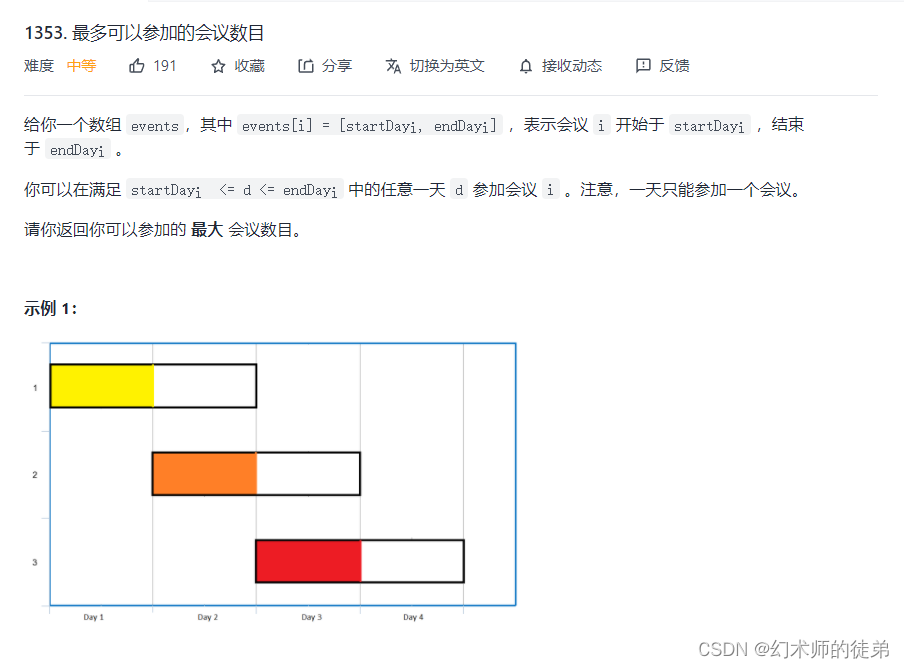
??贪心策略:选择当天已经开始了的会议中结束时间最早的会议参加,因为这样其他的会议可以在别的时间参加。
??那么怎么获得当前已经开始的会议中结束时间最早的会议呢,首先对会议按开始时间排序,然后维护一个小跟堆,堆中的元素是当天已经开始的会议的结束时间,每次先移除已经过期的会议,然后向堆中加入今天开始的会议的结束时间,然后从堆中找到结束时间最早的会议参加,然后进入下一天。
class Solution {
public:
int maxEvents(vector<vector<int>>& events)
{
sort(events.begin(), events.end(), cmp());
int n = events.size();
priority_queue<int, vector<int>, greater<int>> pq;
int curday = 1;
int ret = 0;
int i = 0;
while (i < n || !pq.empty())
{
/*移除过期时间*/
while (!pq.empty() && pq.top() < curday) pq.pop();
/*把今天开始的会议加入堆*/
while (i < n && events[i][0] == curday)
{
pq.push(events[i][1]);
++i;
}
/*选开始最早的会议参加*/
if (!pq.empty())
{
pq.pop();
++ret;
}
++curday;
}
return ret;
}
struct cmp
{
bool operator()(const vector<int>& a, const vector<int>& b)
{
return a[0] < b[0];
}
};
};
八、无重叠区间
链接:无重叠区间
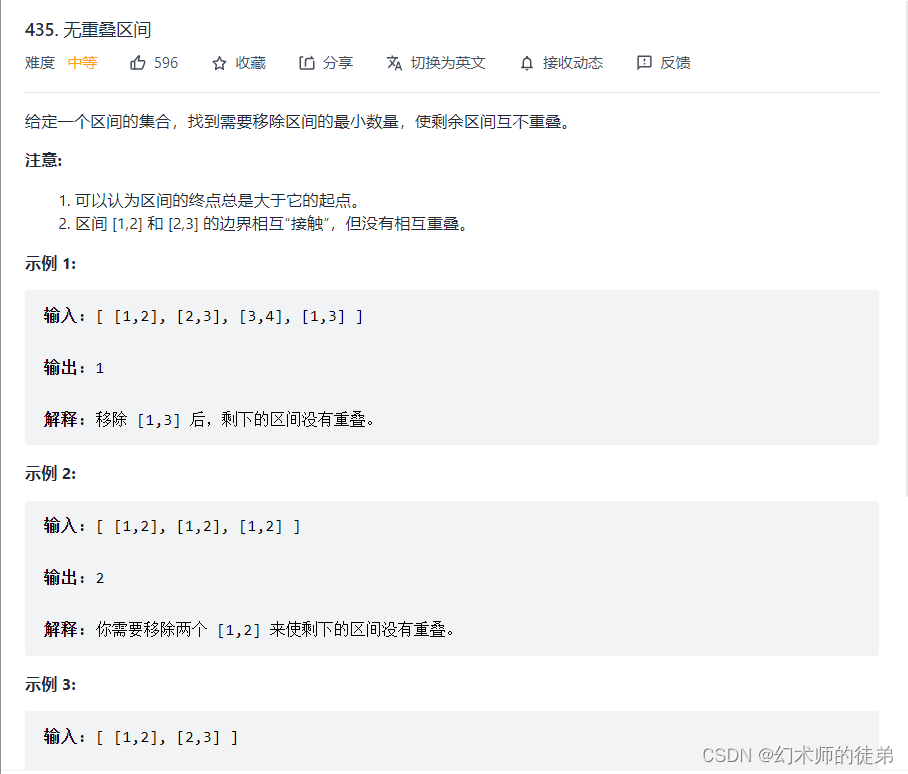
??提供两种贪心算法思路:
??思路1:将本题转化为总区间数减去不重叠区间的最大数量,如果把左区间看做会议的开始时间,右区间看做会议的结束时间,这不就等价于参加会议的最多数量吗,可以用前面的模板解决。
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals)
{
/*先按照结束时间排序*/
sort(intervals.begin(), intervals.end(),
[&](const vector<int>& a, const vector<int>& b){
return a[1] < b[1];
});
/*每次都选结束时间最早的参加*/
int cnt = 1;
int n = intervals.size();
int curmeet = 0;
for (int j = 1; j < n; ++j)
{
if (intervals[curmeet][1] <= intervals[j][0])
{
curmeet = j;
++cnt;
}
}
return n - cnt;
}
};
??思路2:同样转化为最多的不重叠区间数,首先按照左区间排序,然后贪心策略如下:
??记当前组成的不重叠区间序列的最右边一个区间的右端点为prev,如果当前区间的左端点left大于等于prev,则这个区间和前面的区间没有重合,让它入序列,更新prev = right;
??否则如果当前区间的右端点right大于prev,则说明当前区间相对于前一个区间会占用未来要进入的区间的“更多空间”,因此按贪心策略舍弃当前区间,移除区间数+1;
??否则如果当前区间的右端点right小于等于prev,则说明当前区间相对于前一个区间占用未来要将进入的区间的空间更少,按贪心策略舍弃前一区间,让它入序列,prev = right,移除区间数+1;
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals)
{
int n = intervals.size();
int ret = 0;
/*按左区间排序*/
sort(intervals.begin(), intervals.end(),
[&](const vector<int>& a, const vector<int>& b){
return a[0] < b[0];
});
int prev = intervals[0][1];
for (int i = 1; i < n; ++i)
{
/*无重合 不需要移除区间*/
if (prev <= intervals[i][0])
{
prev = intervals[i][1];
}
else if (prev < intervals[i][1])
{
/*有重合且移除i区间*/
++ret;
}
/*为了规避[1,2] [1,2]这种情况 右区间相等的也要移除*/
else if (prev >= intervals[i][1])
{
/*有重合且移除前一区间*/
++ret;
prev = intervals[i][1];
}
}
return ret;
}
};