文章目录
初等数论基础(二)
建议先看
初等数论基础(一)~
一、数论只会gcd
1.1 gcd
(a,b) = (a,a+b) 的证明
(a,a) = (a,0) = a
(a,b) = (a,a+b) = (a,ka+b)

(a,b) = (b,a%b)
(a,b) = (b,a%b)的证明
也叫辗转相除法

注意:gcd(a,b) = 1说明a和b互质。
另外:gcd(1,1) = 1,gcd(a,0) = a,gcd(a,1) = 1
辗转相除法代码:
ll gcd(ll a,ll b)
{
return b?gcd(b,a%b):a;
}
//或者写成
ll gcd(ll a,ll b)
{
if(b==0)
{
return a;
}
return gcd(b,a%b);
}
辗转相除法时间复杂度
只知道是小于log2(b)的呜呜呜
小于log2(b) 很好证:
只需要证a%b<b/2就可以了

1.2 exgcd
啥?除了gcd还有exgcd????
在欧几里得求得gcd(a,b)以后,大家并不满足,于是好奇一个方程的解:
a
x
+
b
y
=
g
c
d
(
a
,
b
)
已
知
a
,
b
,
求
一
组
x
,
y
使
得
方
程
成
立
ax+by = gcd(a,b) \\已知a,b,求一组x,y使得方程成立
ax+by=gcd(a,b)已知a,b,求一组x,y使得方程成立
在将这个方程的解之前需要介绍裴蜀定理:
1.2.1 裴蜀定理
?
a
,
b
,
?
x
,
y
s
.
t
.
a
x
+
b
y
=
g
c
d
(
a
,
b
)
\forall a,b ,\exists x,y \quad s.t. \quad ax+by = gcd(a,b)
?a,b,?x,ys.t.ax+by=gcd(a,b)
哈,其实就是说1.2的方程一定是有解的
1.2.2 ax+by = gcd(a,b)的求解
先构造:
显然当b = 0时,有x = 1,y = 任意值(一般写成0)
对于b!=0的情况:

只要每次先把(2)式求出,那么(1)式的解也能出来了:)
1.2.3 拓展
二、欧拉相关
2.1 欧拉函数

详细定义见:初等数论基础一
2.2 欧拉定理相关
2.2.1 欧拉定理
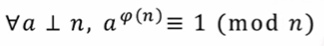
说人话就是:对于任意a与n互质,即有a的φ(n)次方与1在模n意义下同余。
例:
φ
(
7
)
=
6
,
3
φ
(
7
)
=
3
6
%
7
≡
1
(
m
o
d
??
7
)
\varphi(7) = 6,\quad 3^{\varphi(7)} = 3^6\%7 \equiv1(\mod 7)
φ(7)=6,3φ(7)=36%7≡1(mod7)
2.2.1 扩展欧拉定理
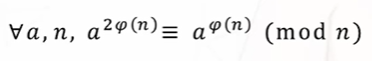
引申:
若
b
>
φ
(
n
)
,
则
a
b
≡
a
b
%
φ
(
n
)
+
φ
(
n
)
(
m
o
d
n
)
若b>\varphi(n),则a^b \equiv a^{b\%\varphi(n)+\varphi(n)}( mod \quad n)
若b>φ(n),则ab≡ab%φ(n)+φ(n)(modn)