1、快速排序
快速排序是基于分治思想的常用于算法竞赛的排序算法
步骤:
1、确定分界点 :q[L]? ? ?q[(L+R)/2]? ? ?q[R]
2、💖调整区间范围:使得小于等于x的在一边,大于等于x的在另一边
3、递归处理左右两边

?重点在于,如何调整区间范围,先说一种很简单的、笨拙的方式(一般不采用):
- 先定义两个数组a[ ]、b[ ],分别装小于等于x、大于等于x的数据
- 遍历q数组,将符合条件的数据分别放在a数组和b数组中
- a数组和b数组,拼接即又组成新的q数组
- 继续递归...

那么最常用的方式是如下双指针的用法,需要背记模板
调整区间范围的经典步骤:
- 选定一个分界点的数x,即:小于x的数要等会放在左边,大于x的数要放在右边? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(一般我们选分界点是数组中点,当然也可以有其他选法)
- 定义两个指针i、j分别指向起始位置得前一位(惯用技巧)和末尾位置后一个位置
- ?i++,然后判断 i 指向得数是否小于 x。如果 i 指向的数小于x,那么 i 继续往后走,即:i++。否则,此时i停住? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?j--,然后判断 j 指向的数是都大于?x。如果 j 指向的数大于x,那么 j 继续往前走,即:j--。否则,j? 停住? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(由于此时i,j都停住,因为他们指向的数都不符合条件【左边放较小的数,右边放较大的数】,所以此时i、j指向的数交换)
- swap(),交换i、j分别指向得数
- 继续i++,j--执行上述判断..................
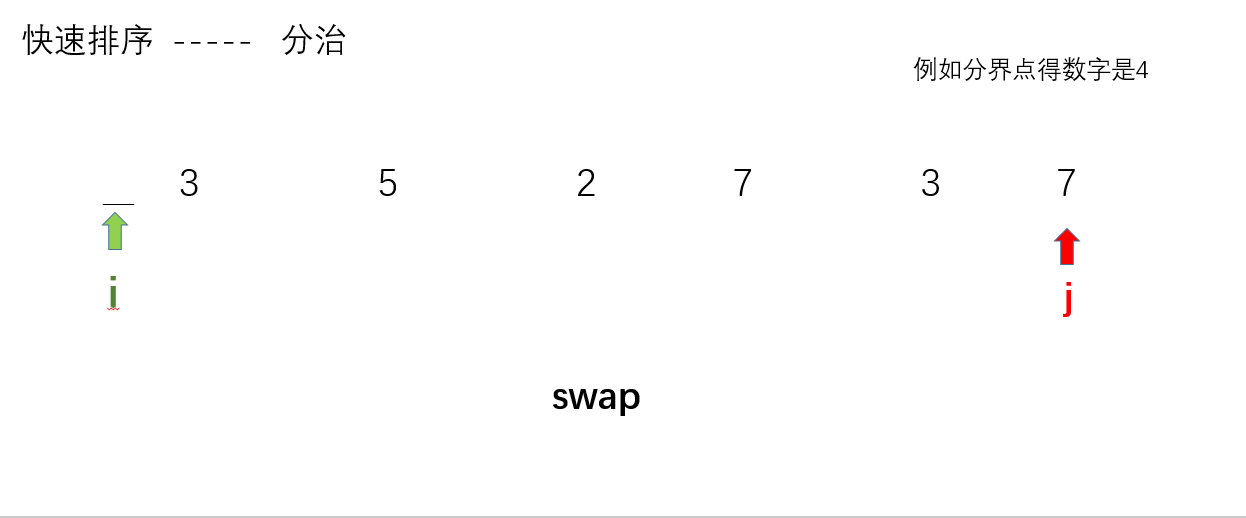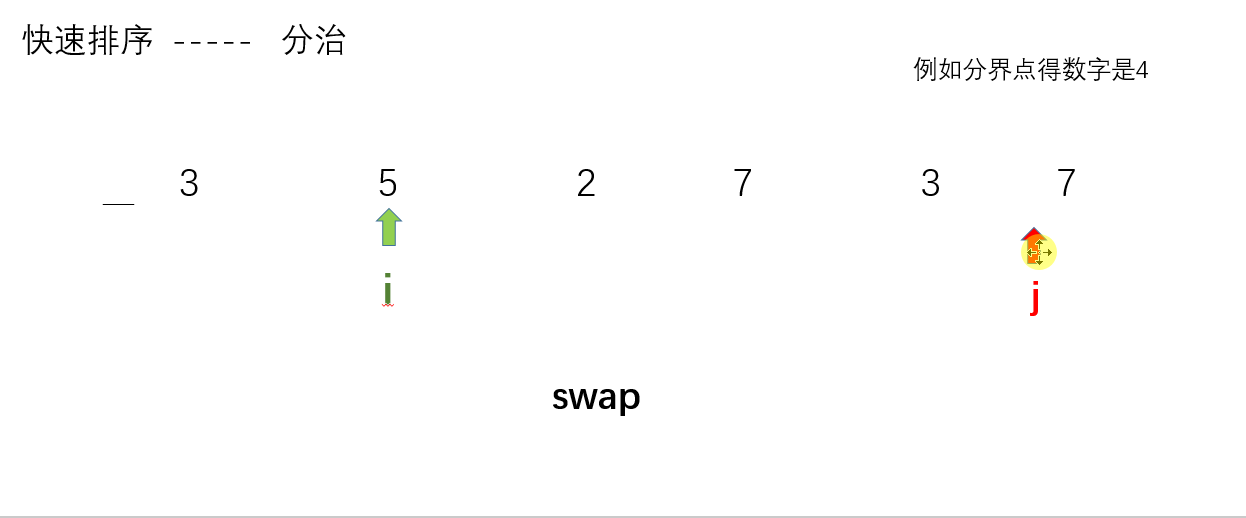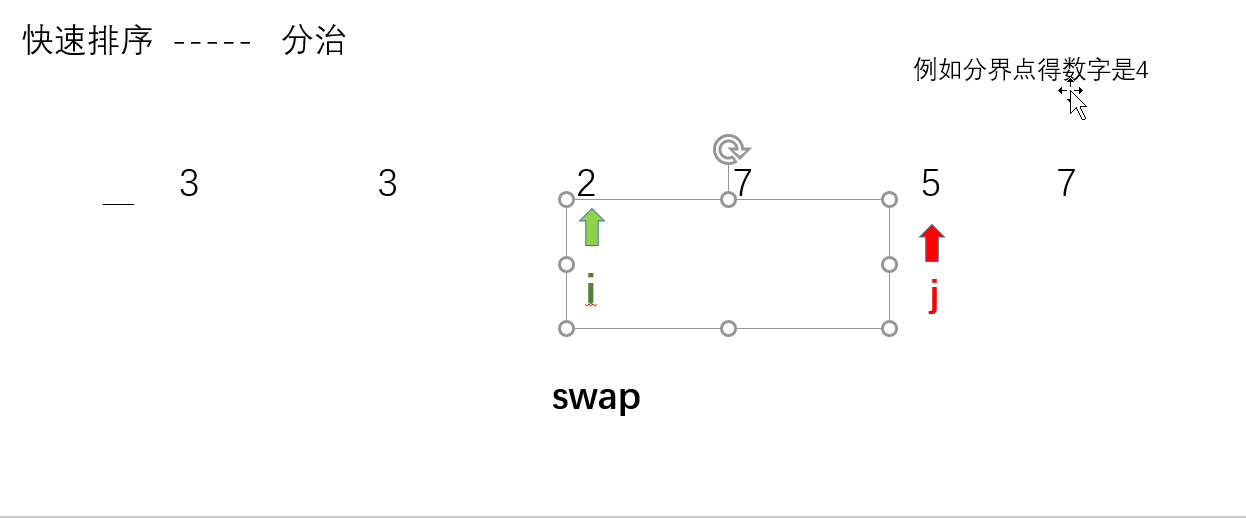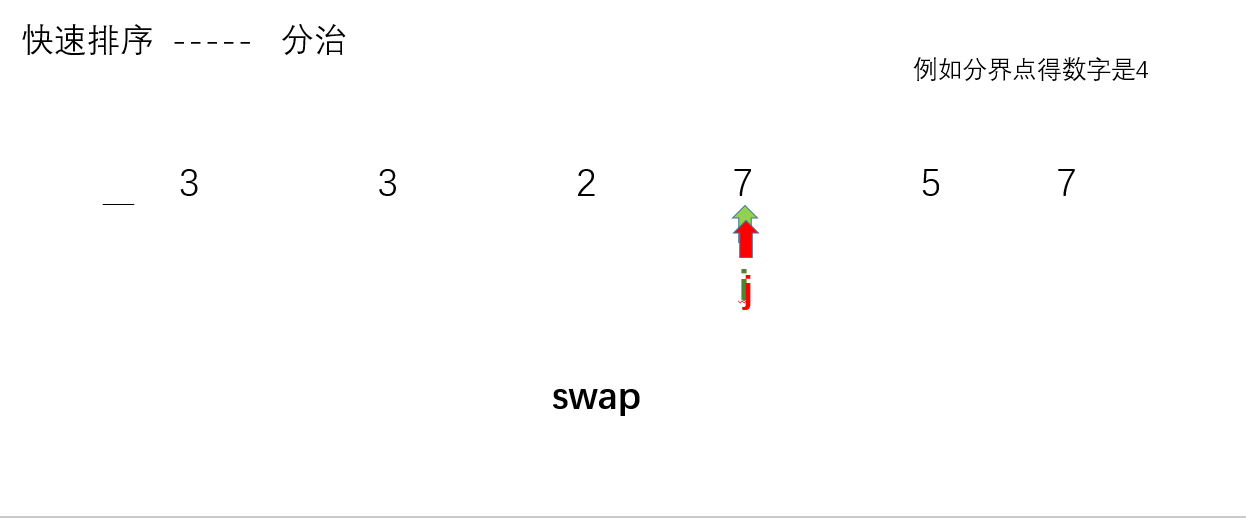
模板
void quick_sort(int q[], int l, int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do ++ i ; while (q[i] < x);
do -- j ; while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}整体应用:
#include<iostream> using namespace std; const int N = 1e6 + 10; int n; int q[N]; void quick_sort(int q[], int l, int r) { if (l >= r) return; int i = l - 1, j = r + 1, x = q[l + r >> 1]; while (i < j) { do ++i; while (q[i] < x); do --j; while (q[j] > x); if (i < j) swap(q[i], q[j]); } quick_sort(q, l, j); quick_sort(q, j + 1, r); } int main() { scanf("%d", &n); for (int i = 0; i < n; i++) scanf("%d", &q[i]); quick_sort(q, 0, n - 1); for (int i = 0; i < n; i++) printf("%d ", q[i]); return 0; }
归并排序
归并排序也是基于分治思想的常用于算法竞赛的排序算法
步骤:
1、确定分界点 :确定分界点:mid = (L + R)/2
2、递归排序left、right
3、归并----合二为一? ?(重点)

?“?? 合二为一?? ”的过程步骤:
由于递归后的左半边的数组和右半边的数组都是有序的。
- 分别定义两个指针,指向两个数组起始位置的数据
- i? 与??j??比较大小,较小的放在res数组中。然后较小的继续往后移动,继续与刚刚的另一个指针所指的数据比较? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (注意:一个数组已经结束,另一个数组还有剩余元素,则直接将剩余元素放在res数组中即可

模板
void merge_sort(int q[], int l, int r)
{
if (l >= r) return;
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
int k = 0, i = l, j = mid + 1;
while (i <= mid && j <= r)
if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
else tmp[k ++ ] = q[j ++ ];
while (i <= mid) tmp[k ++ ] = q[i ++ ];
while (j <= r) tmp[k ++ ] = q[j ++ ];
for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}整体应用:
#include<iostream> using namespace std; const int N = 1e6 + 10; int n; int q[N], tmp[N]; void merge_sort(int q[], int l, int r) { if (l >= r) return; int mid = l + r >> 1; merge_sort(q, l, mid); merge_sort(q, mid + 1, r); int k = 0, i = l, j = mid + 1; while (i <= mid && j <= r) if (q[i] <= q[j]) tmp[k++] = q[i++]; else tmp[k++] = q[j++]; while (i <= mid) tmp[k++] = q[i++]; while (j <= r) tmp[k++] = q[j++]; for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j]; } int main() { scanf("%d", &n); for (int i = 0; i < n; i++) scanf("%d", &q[i]); merge_sort(q, 0, n - 1); for (int i = 0; i < n; i++) printf("%d ", q[i]); return 0; }
对比如下几种排序,我们发现差别不大
- 快速排序
- sort函数(注意:在头文件#include<algorithm>中)
- 归并排序

?当然,更方便的是sort,C++中在头文件#include<algorithm>中的库函数
下面是sort函数的用法
#include<algorithm>中的Sort函数使用用法
1、sort函数包含在头文件为#include<algorithm>的c++标准库中,调用标准库里的排序方法可以实现对数据的排序,但是sort函数是如何实现的,我们不用考虑!
2、sort函数的模板有三个参数:
void sort (RandomAccessIterator first, RandomAccessIterator last, Compare comp);(1)第一个参数first:是要排序的数组的起始地址。
(2)第二个参数last:是结束的地址(最后一个数据的后一个数据的地址)
(3)第三个参数comp是排序的方法:可以是从升序也可是降序。如果第三个参数不写,则默认的排序方法是从小到大排序。
#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
//sort函数第三个参数不写,则采用默认从小到大
int a[] = {45,12,34,77,90,11,2,4,5,55};
sort(a, a+10);
for(int i = 0;i < 10;i++)
cout << a[i] << " ";
}运行结果:

#include<iostream>
#include<algorithm>
using namespace std;
bool cmp(int a,int b);
main(){
//sort函数第三个参数自己定义,实现从大到小//需要特别注意!
int a[]={45,12,34,77,90,11,2,4,5,55};
sort(a,a+10,cmp);
for(int i=0;i<10;i++)
cout<<a[i]<<" ";
}
//自定义函数
bool cmp(int a,int b){
return a > b;
}运行结果:

整数二分
搭配B站资源,才听懂的,嘤嘤嘤~

总结:
整数二分中,有两个模板,一个是找符合条件的出现的第一个数字;一个是找符合条件的出现的最后一个数字
对于符合条件的出现的第一个数字,我们需要注意的是:
mid = (l + r) >> 1;对于符合条件的出现的最后一个数字,我们需要注意的是:
mid = (l + r + 1) >> 1;他俩的mid是有区别的。
那么为什么,符合条件的出现的最后一个数这种情况中的mid需要分子上 + 1呢?
假设我们不补上+1,那么如果不巧,是l = r - 1,即:相差一个数的时候
那么mid = (l + r) / 2,向下取整mid = (2l - 1) / 2 = l。那么if(check(mid)) 如果是true,那么l = mid即:l = l,那么继续往下循环就会是死循环
而如果我们补上+ 1,那么当处于这种边界l = r - 1时,那么mid = (l + r + 1) / 2,向下取整mid = (2r) / 2 = r。那么if(check(mid)) 如果是true,那么l = mid即:l = r,那么继续往下循环最终就会[r,r]结束循环
模板
注意:最后返回的是 l 下标
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
// 符合条件的第一个
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
// 符合条件的最后一个
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}整体应用1:(拿 符合条件的出现的第一个数字? ?举例)(洛谷P2249)
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int n, m, a[N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);//注意,该处写法与下面l和r的初始值有关
while (m--)
{
int x;
scanf("%d", &x);
int l = 1, r = n;//注意l从1开始,r是n
while (l < r)
{
int mid = (l + r) >> 1;
if (a[mid] >= x)r = mid;
else l = mid + 1;
}
if (a[l] != x) cout << -1 << " ";
else cout << l << " ";
}
return 0;
}整体应用2:acwing数的范围
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int n, q, a[N];
int main()
{
scanf("%d%d",&n,&q);
for(int i = 0;i < n;i++) scanf("%d",&a[i]);
while(q--)
{
int x;
scanf("%d",&x);
int l = 0,r = n - 1;
//符合条件的第一个出现的数
while(l < r)
{
int mid = (l + r) >> 1;
if(a[mid] >= x) r = mid;
else l = mid + 1;
}
if(a[l] != x) cout << -1 << " ";
else cout << l << " ";
l = 0,r = n - 1;
//符合条件的最后一个出现的数
while(l < r)
{
int mid = (l + r + 1) >> 1;
if(a[mid] <= x) l = mid;
else r = mid - 1;
}
if(a[l] != x) cout << -1 ;
else cout << l ;
cout << endl;
}
return 0;
}浮点数二分
看图自己理解,不仔细画了.........?

模板
bool check(double x) {/* ... */} // 检查x是否满足某种性质
double bsearch_3(double l, double r)
{
const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求
while (r - l > eps)
//for(int i =0;i < 100;i++)//不管三七二十一,循环迭代100次,精度肯定满足要求
{
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}整体应用:acwing数的三次方根
#include<iostream>
using namespace std;
int main()
{
double n;
cin >> n;
double l = -10000, r = 10000;//注意,三次方不要求根号下是正数;【注意题目所给的范围!】
//for(int i = 0;i < 100;i++)//循环迭代100次
while(r - l > 1e-8)
{
double mid = (l + r) / 2;
if(mid * mid * mid >= n) r = mid;
else l = mid;
}
printf("%.6lf\n",l);
return 0;
}技巧:
如果题目说要保留几位小数,那么我在while()循环判断的时候,最好是要比该保留小数点位数多两个。这样一定不会精度损失
比如说:保留6位小数,那么我循环判断的时候就可以写while(r - l > 1e-8)