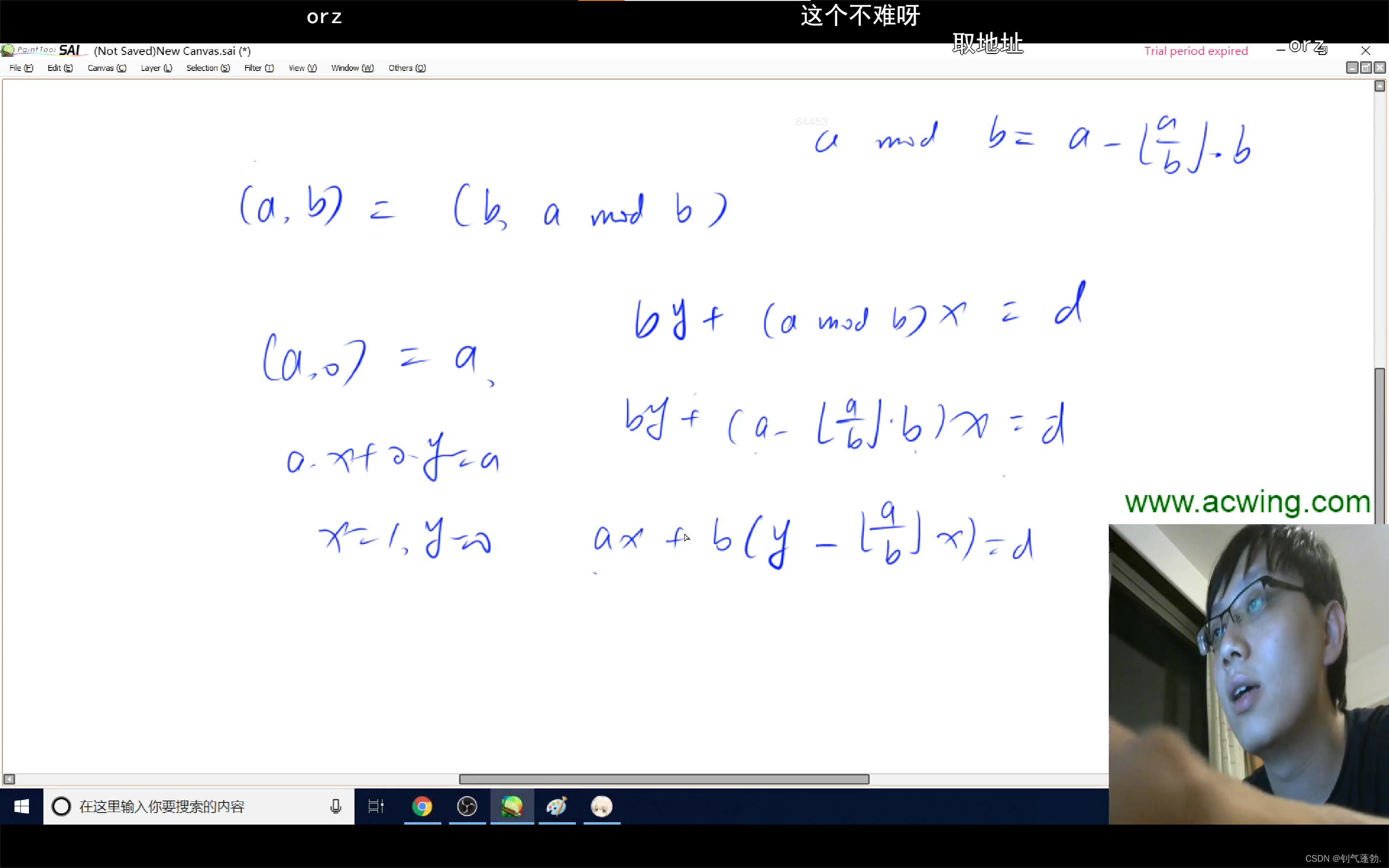
1 扩展欧几里得算法
?
/*
学acwing的算法基础课学来的,喜欢的话多多支持呀。
*/
//扩展欧几里得算法求 a*x+b*y=gcd(a,b)求x,y
#include<bits/stdc++.h>
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{
if(!b)//假如b为0 ,则x为1,y为0
{
x=1,y=0;
return a;//返回最小公倍数为a
}
int d=exgcd(b,a%b,y,x);//d为最小公倍数
y-=a/b*x;//根据推理得来的,y更新为这个
return d;//返回最小公倍数
}
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
int a,b,x,y;
scanf("%d%d",&a,&b);
exgcd(a,b,x,y);
printf("%d %d\n",x,y);//输出符合条件的x,y
}
return 0;
}
/*到达胜利之前无法回头*/
/*
学acwing的算法基础课学来的,喜欢的话多多支持呀。
*/
//扩展欧几里得算法求 a*x+b*y=gcd(a,b)求x,y变形为线性同余方程 a*x(mod m)≡b -> a*x-y*m=b(y为整数)
#include<bits/stdc++.h>
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{
if(!b)//假如b为0 ,则x为1,y为0
{
x=1,y=0;
return a;//返回最小公倍数为a
}
int d=exgcd(b,a%b,y,x);//d为最小公倍数
y-=a/b*x;//根据推理得来的,y更新为这个
return d;//返回最小公倍数
}
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
//a*x(mod m)≡b -> a*x-y*m=b(y为整数)
int a,b,x,y,m;
scanf("%d%d%d",&a,&b,&m);
int d=exgcd(a,m,x,y);//根据推理变形得a*x-y*m=b(y为整数)
if(b%d) puts("impossible");//假如b不是a和m的最小公倍数的倍数
else printf("%d\n",(long long)x*(b/d)%m);//否则有答案,为把d变成b则两边都乘以b/d,因为算出来的是d,而我们的另一边是b
}
return 0;
}
/*到达胜利之前无法回头*/
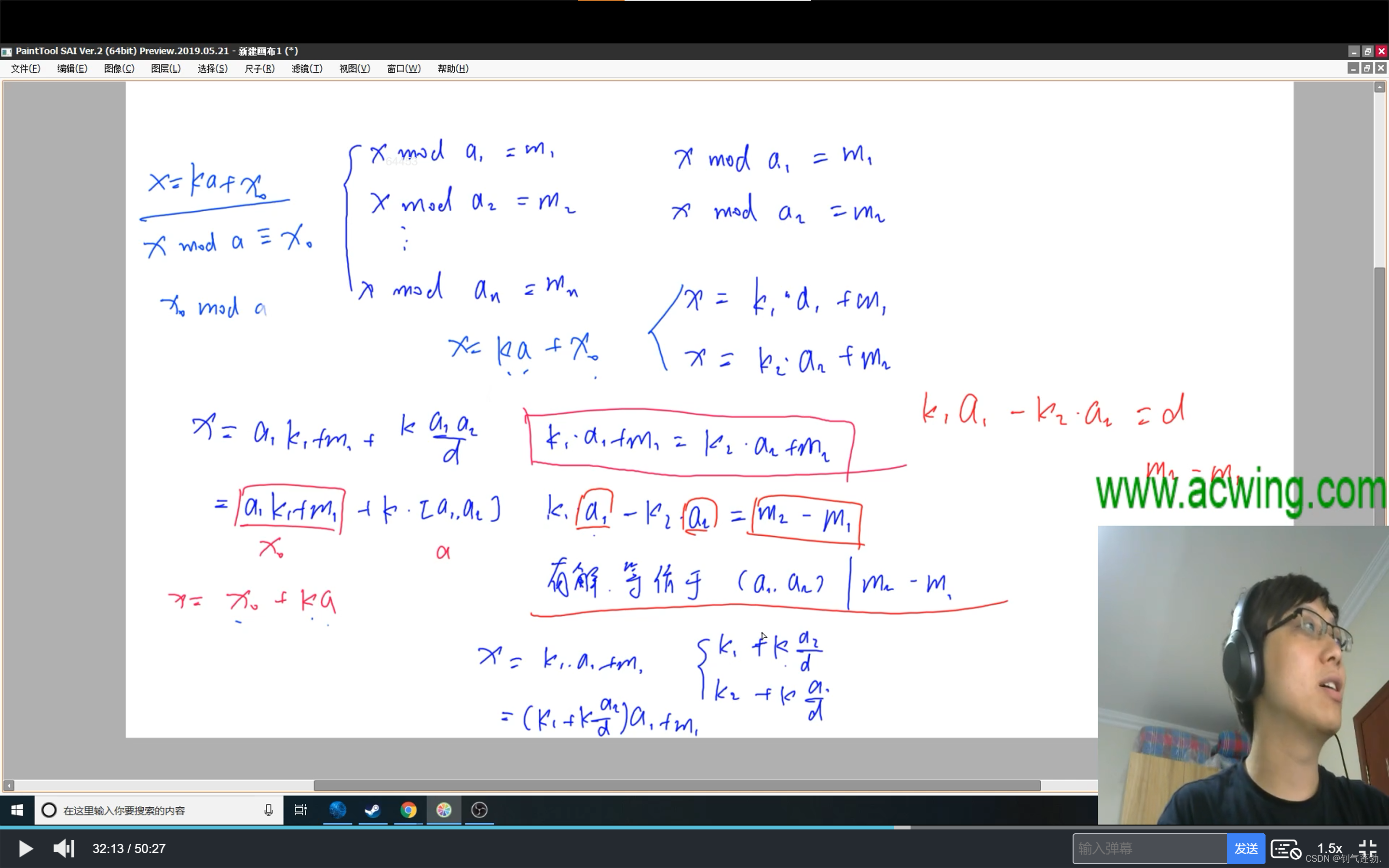
?2 中国剩余定理
?
/*
学acwing的算法基础课学来的,喜欢的话多多支持呀。
*/
//中国剩余定理 x(mod a)≡m;求x,用扩展欧几里得算法
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll exgcd(ll a,ll b,ll &x,ll &y)//扩展欧几里得算法模板
{
if(!b)
{
x=1,y=0;
return a;
}
ll d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int main()
{
int n;
cin >> n;
bool has_answer=true;//用来判断有没有答案
ll m1,a1;
scanf("%lld%lld",&a1,&m1);
for (int i=0;i<n-1;i++)
{
ll m2,a2;
scanf("%lld%lld",&a2,&m2);
ll k1,k2;
ll d=exgcd(a1,a2,k1,k2);//求a1与a2的扩展欧几里得算法
if ((m2-m1)%d)//假如等式右边的数不能整除最小公倍数,则没答案
{
has_answer=false;
break;
}
k1*=(m2-m1)/d;//因为用扩展欧几里得得到的等式右边是d,为了变成m1-m2,则等式左右两边都乘以(m2-m1)/d
ll t=a2/d;//图片的通式
k1=(k1%t+t)%t;//因为c++膜出来的结果有负数,这样就能把摸出来的保证为正数
m1=a1*k1+m1;//新的m1,对比原式得来
a1=abs(a1/d*a2);//新的a1,对比原式得来
}
if (has_answer) printf("%lld\n",(m1%a1+a1)%a1);//输出答案
else puts("-1");
return 0;
}
/*到达胜利之前无法回头*/