一、全息干涉图的生成
在最简单的情况下,干涉图(全息图)是由畸变光束(物光)与平面波(参考光)混合产生的。
首先,模拟一束畸变光束(物光),其相位如下图所示:
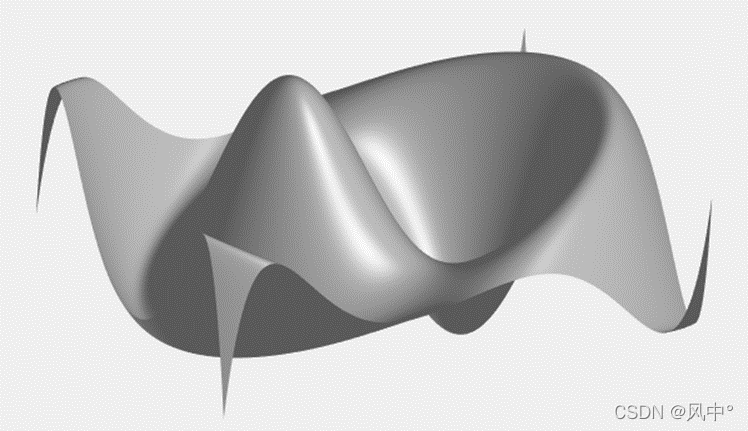
模拟生成平面参考光,其相位如下图所示:

参考光与物光叠加之后获取的全息图如下所示:

二、相位重构
为了全息干涉图中获得重构相位,本文使用傅里叶域中的平移与滤波处理来重构波前相位。
上述全息干涉图可表述为:
g ( x , y ) = c ( x , y ) exp ? ( 2 π i f 0 x ) + c ? ( x , y ) exp ? ( ? 2 π i f 0 x ) g\left( x,y \right)=c\left( x,y \right)\exp (2\pi i{{f}_{0}}x)+{{c}^{*}}\left( x,y \right)\exp (-2\pi i{{f}_{0}}x) g(x,y)=c(x,y)exp(2πif0?x)+c?(x,y)exp(?2πif0?x) (1)
其中,
c ( x , y ) = 1 2 exp ? ( i ψ ( x , y ) ) c\left( x,y \right)=\frac{1}{2}\exp \left( i\psi (x,y) \right) c(x,y)=21?exp(iψ(x,y)) (2)
ψ ( x , y ) \psi (x,y) ψ(x,y)包含了物体信息, f 0 x {{f}_{0}}x f0?x描述了波前倾斜。上式进行傅里叶变换后,可得:
G ( f , y ) = A ( f , y ) + C ( f + f 0 , y ) + C ? ( f ? f 0 , y ) G\left( f,y \right)=A\left( f,y \right)+C(f+{{f}_{0}},y)+{{C}^{*}}(f-{{f}_{0}},y) G(f,y)=A(f,y)+C(f+f0?,y)+C?(f?f0?,y) (3)
其中大写字母A和C表示傅里叶谱,f表示空间频率。我们可以从两个旁瓣谱 C ( f + f 0 , y ) C(f+{{f}_{0}},y) C(f+f0?,y)或 C ? ( f ? f 0 , y ) {{C}^{*}}(f-{{f}_{0}},y) C?(f?f0?,y)中选取一个,并将其转换为零空间频率的原点。接着,我们可以对转换后的光谱进行傅里叶逆变换,得到表达式(1)中定义的c(x,y)。计算表达式(2)的复对数,可得到相位 ψ ( x , y ) \psi (x,y) ψ(x,y):
i ψ ( x , y ) = log ? [ c ( x , y ) ] i\psi (x,y)=\log \left[ c\left( x,y \right) \right] iψ(x,y)=log[c(x,y)] (4)
相位 ψ ( x , y ) \psi (x,y) ψ(x,y)不确定为因子2π,其主值位于-π-π范围内。为了获得连续相位图,对重建的相位图采用了一种特殊的解包裹算法,去除振幅接近2π的不连续性。算法实现包括以下步骤:
1) 对仅含物光场的全息图进行傅里叶变换,此时频谱由一个中央瓣和两个包含相位信息的副瓣组成。
2)取出其中一个旁边并放入原点。(滤波处理)
3)逆傅里叶变换
4)求出重构相位
重构相位如下图所示

三、资源获取
上述仿真程序可从以下链接处获取: