一、定义

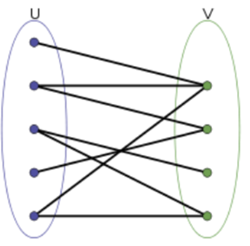
??图的节点由两个集合 u、v 组成，且两个集合内部没有边的图，图中不存在奇数环（配合下图来看）
在这里插入图片描述

二、应用

算法种的应用：
??①判断二分图：染色法
??②求二分图最大匹配树：匈牙利法
??
实际中的应用：
??大体来说是具有匹配性质的用途都可以用二分图来解决。如：分配工作使尽可能多的人做自己擅长的事 (擅长度间的匹配)、超市里装最少摄像头来覆盖整个超市 (范围大小间的匹配)、分配监狱罪犯时减少确保同个监狱里最少仇恨度 (仇恨度大小间的匹配) 、两台机器中多模式的任务调度问题 (模式之间的匹配) 等等……

三、算法模板

在这里插入图片描述
👉染色法的应用：点这里
👉匈牙利法模板练习：点这里
Attention：使用模板前，请先判断是稀疏图、稠密图
?

① 染色法模板

在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5+10, M = 2e5+10;

int n, m;
int h[N], e[M], ne[M], idx;
int color[N];

void add(int a, int b){
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool dfs(int u, int c){
	color[u] = c;
	
	for(int i = h[u]; i != -1; i = ne[i]){
		int j = e[i];							//j为 i 指向的点
		if(!color[j])
			//没有染过色的话就去染下色
			if(!dfs(j, 3 - c)) return false;	//3-c，把1的染成2，2的染成1
		else if(color[j] == c) return false;	//如果颜色相同，则不符合染色法的概念
	}
	return true;
}

int main(){
	scanf("%d %d\n", &n, &m);
	memset(h, -1, sizeof h);
	while(m--){
		int a, b;
		scanf("%d %d", &a, &b);
		add(a, b), add(b, a);				//无向图
	}
	
	bool flag = true;
	for(int i = 1; i <= n; i++)
		if(!color[i])
			if(!dfs(i, 1)){
				flag = false;
				break;
			}
	if(flag) puts("Yes");
	else puts("No");
	
	return 0;
}

② 匈牙利模板 - 邻接表

#include <bits/stdc++.h>
using namespace std;

const int N = 510, M = 5e4+10;

int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];

void add(int a, int b){
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool find(int x){
	for(int i = h[x]; ~i; i=ne[i]){
		int j = e[i];
		if(!st[j]){
			st[j] = true;
			//如果这个妹子没有匹配过男生的话，或者说能为匹配过的男生找到下家妹子(把当前这个妹子让出来)
			if(match[j] == 0 || find(match[j])){
				match[j] = x;
				return true;
			}
		}
	}
	return false;
}

int main(){
	scanf("%d%d%d", &n1, &n2, &m);
	while(m--){
		int a, b;
		scanf("%d%d", &a, &b);
		add(a, b);
	}
	
	int res = 0;						//匹配的数量
	for(int i = 1; i <= n2; i++){
		memset(st, false, sizeof st);	//保证右半部(妹子集合)只考虑一遍
		if(find(i)) res++;
	}
	printf("%d\n", res);
	
	return 0;
}

③ 匈牙利模板 - 邻接矩阵

#include <bits/stdc++.h>
using namespace std;

const int N = 510;

int n1, n2, m;
int g[N][N], match[N];
bool st[N];

bool dfs(int x){
	for(int i = 1; i <= n2; i++){
		if(!st[i] && g[x][i]){		//如果没有访问过，并且存在 x 到 i 的边
			st[i] = true;
			if(match[i] == 0 || dfs(match[i])){
				match[i] = x;
				return true;
			}
		}
	}
	return false;
}

int main(){
	scanf("%d%d%d", &n1, &n2, &m);
	while(m--){
		int a, b;
		scanf("%d%d", &a, &b);
		g[a][b] = 1;					//存在 a 到 b 的边
	}
	
	int res = 0;						//匹配的数量
	for(int i = 1; i <= n1; i++){
		memset(st, false, sizeof st);
		if(dfs(i)) res++;
	}
	printf("%d\n", res);
	
	return 0;
}