开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【从零开始的嵌入式生活】数据结构2——线性表及顺序表 -> 正文阅读

[数据结构与算法]【从零开始的嵌入式生活】数据结构2——线性表及顺序表

请添加图片描述

前言

今天开了个新正式进入数据结构的学习，这两天颈椎病需要治一治所以有些拖更，治好我就满血复活0.0大家注意身体呀！
另外今天竟然接到了第一个实习的面试邀请，惊喜，这两天也会加油更新的同时看看面经，相关的过程记录我也想更新，如果大家想看的话（疯狂暗示）。
主要内容为：
请添加图片描述

三连即可提高学习效率0.0

🧑🏻作者简介：一个学嵌入式的年轻人
?联系方式：2201891280(QQ)
📔源码地址：https://gitee.com/xingleigao/study_qianrushi
?全文大约阅读时间： 60min

线性表

线性表是包含若干数据元素的一个线性序列
记为：L=(a₀,…a_i-1,a_i,a_i+1,…a_n-1)

L为表名，a_i(0 $\leqslant$ i $\leqslant$ n-1)为数据元素；
n为表长,n>0是，线性表L为非空表，否则为空表。

线性表L可用二元组形式描述：L=(D,R)
即线性表L包含数据元素集合D和关系集合R

举个例子：
设L={1,2,3,4,5,6}关系如图：

使用二元组描述为L=(D,R)其中D={1,2,3,4,5,6}(n=6),R={<1,2>,<2,3>,<3,4>,<4,5>,<5,6>}

线性表的特征

对非空表，a₀是表头，无前驱；
a_n-1是表尾，无后继；
其它的每个元素a_i有且仅有一个直接前驱a_i-1和一个直接后继a_i+1。

其实就是上图的表示方式

线性表的顺序存储

将线性表L=(a~0~,....a~i-1~,a~i~,a~i+1~,...a~n-1~)中各元素依次存储在计算机一片连续的存储空间。
请添加图片描述
则假设Loc(a~i~)为a~i~的地址，Loc(a₀)=b,则有：Loc(a~i~) = b + i * d

顺序存储的特点：

优点
- 逻辑上相邻的元素a_i，a_i+1，其存储位置也相邻
- 对数据元素a_i的存取为随机存取或按地址存取
- 存储密度高
  - 存储密度D = (数据结构中元素所占存储空间)/(整个数据结构所占空间)
缺点
- 对表的插入和删除等运算时间复杂度高

看问题应用场景，其实任何方式都有优缺点都有其应用场景，只有相对较好的解决方案，没有正确的解决方案！

顺序存储的定义方式

在C语言中，可借助于一维数组类型来描述。
线性表的顺序存储结构

#define N 100
typedef int data_t; //可以改变数据类型定义其他的类型数据
typedef struct{
	data_t data[n]; //表的存储空间
	int last;
}sqlist,*sqlink;

代码的写作规范

一般的写作包含三部分内容sqlist.h、sqlist.c、test.c

sqlist.h包含定义、运算
sqlist.c包含函数的接口实现

代码分层的原因：请添加图片描述
其中外包公司用的时候为了保护公司核心资产所以只会给.h和编译好的.s.o。所以.h文件一般暴露接口定义和基本的数据结构定义。

所以可以使用两种方式编译：

#一个个编译
gcc -c test.c sqlist.c	#编译生成test.o和sqlist.o
gcc *.o -o a.out	#编译生成a.out
#一起编译
gcc *.c -o a.out

所以给外包公司汇编好的.o即可，头文件也需要给到就完事了。

线性表的基本运算

建立一个空表：list_create(L)

请添加图片描述

sqlink list_create(){
       //malloc
       sqlink L;

       L = (sqlink)malloc(sizeof(sqlist));
       if ( L == NULL){
               printf("list malloc failed\n");
               return L;
       }

       //initialize
       memset(L, 0, sizeof(sqlist));
       L->last = -1;

       //return
       return L;
}

置空表：list_clear(L)

/*
* @ret 0-success -1-failed
* */
int list_clear(sqlink L){
       if(L == NULL)
               return -1;

       memset(L, 0, sizeof(sqlist));
       L->last = -1;

       return 0;
}

判空：list_empty(L) 空返回`1`，非空为`0`

/*
* list_empty : Is list empty?
* para L : list
* @ret 1--empty 0--not empty  -1--failed
* */
int list_empty(sqlink L){
       if (L == NULL)
               return -1;
       if (L->last == -1)
               return 1;
       else
               return 0;
}

求表长：length(L)

/*
* list_length : return the length of list
* para L : list
* @ret -1--failed
* */
int list_length(sqlink L){
       if (L == NULL)
               return -1;
       return (L->last + 1);
}

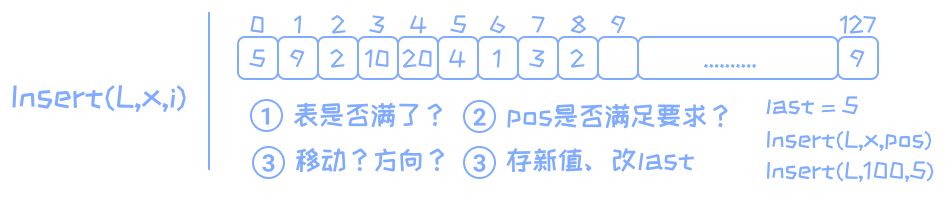
插入：Insert(L,x,i)将元素x插入到表L中第i个元素`a~i~`之前，且表长`+1`

请添加图片描述
其中的三个问题：

last < (N - 1)
$\leqslant pos \leqslant last+1$
如果在last+1插入不需要移动，否则从后往前依次移动。

int list_insert(sqlink L, data_t value, int pos){
       int i;

       if (L == NULL)
               printf("list is invalid\n");

       //full
       if (L->last == N-1){
               printf("list is full\n");
               return -1;
       }

       //check para pos [0, last+1]
       if ( pos < 0 || pos > L->last+1){
               printf("Pos is invalid\n");
               return -1;
       }

       //move
       for (i = L->last; i >= pos; i--){
               L->data[i+1] = L->data[i];
       }

       //update last
       L->data[pos] = value;
       L->last ++;
       return 0;
}

释放空间：list_free(sqlink L);

int list_free(sqlink L){
       if (L == NULL)
               return -1;
       free(L);
       L = NULL;
       return 0;
}

显示所有元素：list_show(sqlink L);

int list_show(sqlink L){
       int i;
       if(L == NULL)
               return -1;
       if(L->last == -1)
               printf("list is empty\n");
       for (i = 0; i <= L->last; ++i){
               printf("%d ", L->data[i]);
       }
       puts("");

       return 0;
}

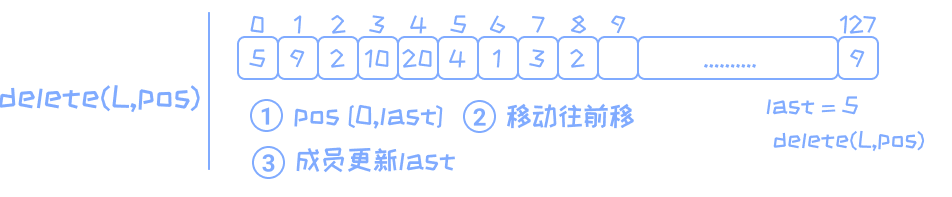
显示所有元素：list_delete(sqlink L, int pos);

请添加图片描述

int list_delete(sqlink L, int pos){
       if (L == NULL){
               printf("list is invalid\n");
               return -1;
       }
       if (L->last == -1){
               printf("list is empty\n");
               return -1;
       }
       //pos [0,last]
       if (pos < 0 || pos > L->last){
               printf("delete pos is invalid\n");
               return -1;
       }
       //move
       for (int i = pos + 1; i <= L->last; i++){
               L->data[i-1] = L->data[i];
      }
       //update
       L->last --;
       return 0;
}

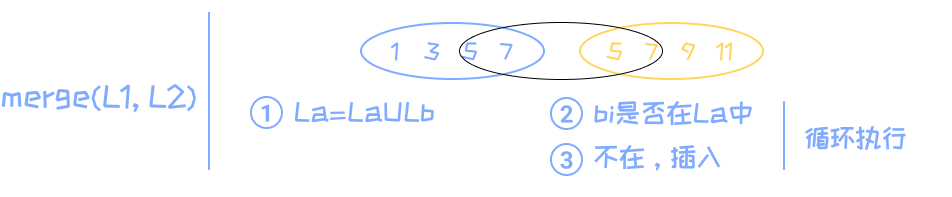
合并链表：list_merge(sqlink L1, sqlink L2)

请添加图片描述

int list_merge(sqlink L1, sqlink L2){
       int i = 0;
       while (i <= L2->last){
               int ret = list_locate(L1, L2->data[i]);
               if (ret == -1){
                       if(list_insert(L1, L2->data[i], L1->last + 1) == -1)
                               return -1;
               }
               ++i;
       }
       return 0;
}

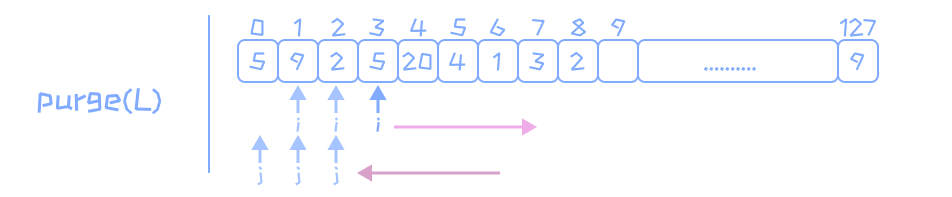
删除线性表中重复的元素：list_purge(sqlink L)

请添加图片描述

int list_purge(sqlink L){
       int i = 1, j;

       if (L->last == 0)
               return 0;
       while ( i <= L->last){
               j = i - 1;
               while ( j >= 0){
                       if (L->data[i] == L->data[j]){
                               list_delete(L, i);
                               break;
                       }
                       else{
                               j--;
                       }
               }
               if (j < 0)
                       i++;
       }

       return 0;
}

线性表的顺序存储优缺点

线性表的顺序存储结构有存储密度高和随机存取的优点
缺点：

要求系统提供一片较大的连续存储空间
插入、删除等运算耗时，且存在元素在存储器中成片移动的现象

写在最后

数据结构开篇之作，今天很多内容需要去gitee仓库里找我练习的代码跟着写来理解，大家加油，接下来的几天时间会继续了解各种数据结构，因为这部分之前我没写完所以更新有点慢，大家和我一起变强呀！最后三连即可提高学习效率！！！

另外我在更新的就是算法笔记的一些例题笔记，这个系列是用于提高我的算法能力，如果有兴趣对算法领域感兴趣找不到合适的入门文章也可以追更，如果我更新的太慢了请大家点赞收藏，一键三连才能更有更新的动力呀0.0