●🧑个人主页:你帅你先说.
●📃欢迎点赞👍关注💡收藏💖
●📖既选择了远方,便只顾风雨兼程。
●🤟欢迎大家有问题随时私信我!
●🧐版权:本文由[你帅你先说.]原创,CSDN首发,侵权必究。
🏂快速排序基本思想及其代码实现
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
快排每一趟都会有一个元素回到它真正的位置。
每次排序选定的轴值就是它最终的位置,所以i次排序后,至少有i个元素确定最终位置。
🥽1. hoare版本
图解
一般选最左边做key,单趟排序以后的目标:左边的值比key小,右边的值比key要大
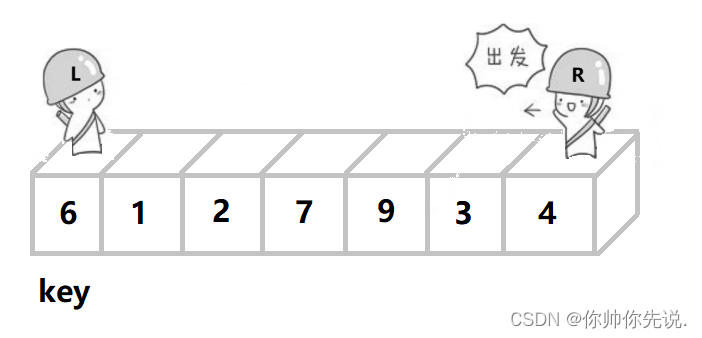
R先出发,找比key小的值,找到后,L后出发,找比key要大的值,找到后两个值交换。
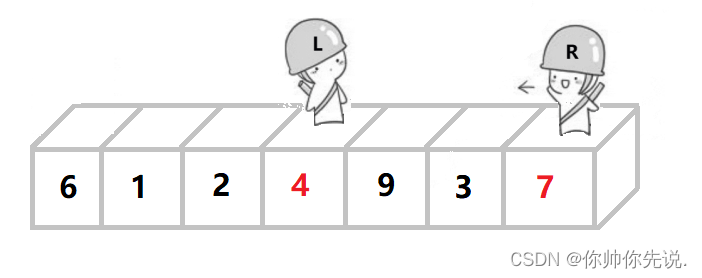
R继续出发,重复上述步骤。
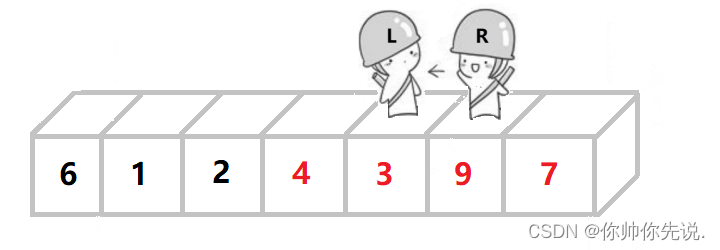
R继续出发直至相遇,相遇点的值和key值交换,一趟排序后,比key小的值在左边,比key大的值在右边。
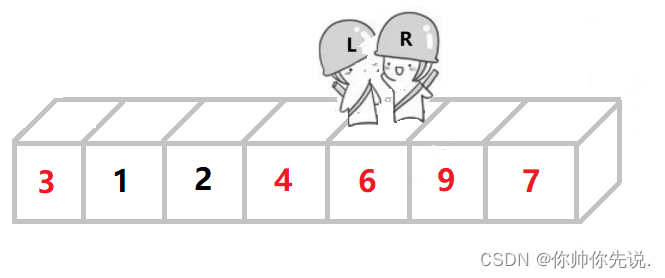
快速排序要记住一个原则。
选最左边做key,右边先走。相遇时的值比key小。
选最右边做key,左边先走。相遇时的值比key大。
过程我们知道了,我们来用代码实现一下
void Partion(int* a,int left,int right)
{
int keyi = left;
while(left < right)
{
//右边先走,找小
while(a[right] > a[keyi])
{
right--;
}
//左边再走,找大
while(a[left] < a[keyi])
{
left++;
}
Swap(&a[left],&a[right]);
}
Swap(&a[left],&a[keyi]);
}
这段代码看似写完了,实际上我们已经写出bug了。
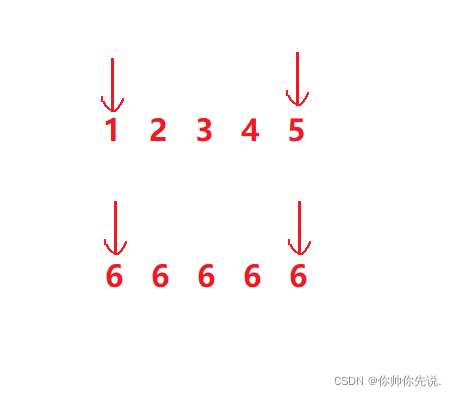
你会发现当遇到这两种情况时,这个排序就出问题了。
写出这个bug的原因是因为没有考虑到相等的情况。
void Partion(int* a,int left,int right)
{
int keyi = left;
while(left <= right)
{
//右边先走,找小
while(a[right] >= a[keyi])
{
right--;
}
//左边再走,找大
while(a[left] <= a[keyi])
{
left++;
}
Swap(&a[left],&a[right]);
}
Swap(&a[left],&a[keyi]);
}
补上这种情况,对着刚刚的图走一遍,发现代码还是有问题,右边的值一直大于key,right的值一直递减,最终会导致数组越界。所以还要限制一下right的范围。
int Partion(int* a,int left,int right)
{
int keyi = left;
while(left <= right)
{
//右边先走,找小
while(left < right && a[right] >= a[keyi])
{
right--;
}
//左边再走,找大
while(left < right && a[left] <= a[keyi])
{
left++;
}
Swap(&a[left],&a[right]);
}
Swap(&a[left],&a[keyi]);
return left;
}
这样这个单趟的快速排序就完美了。
单趟排完后,这些数被分为了两个区间,一个是[left,keyi-1],另一个是[keyi+1,right],然后分别对这两个区间再进行一次单趟的排序,很明显这里要用递归。
void QuickSort(int* a,int left,int right)
{
if(left >= right)
return;
int keyi = Partion(a,left,right);//接收key的下标值
QuickSort(a,left,keyi-1);
QuickSort(a,keyi+1,right);
}
时间复杂度:O(
N
?
l
o
g
2
N
N*log_2N
N?log2?N)
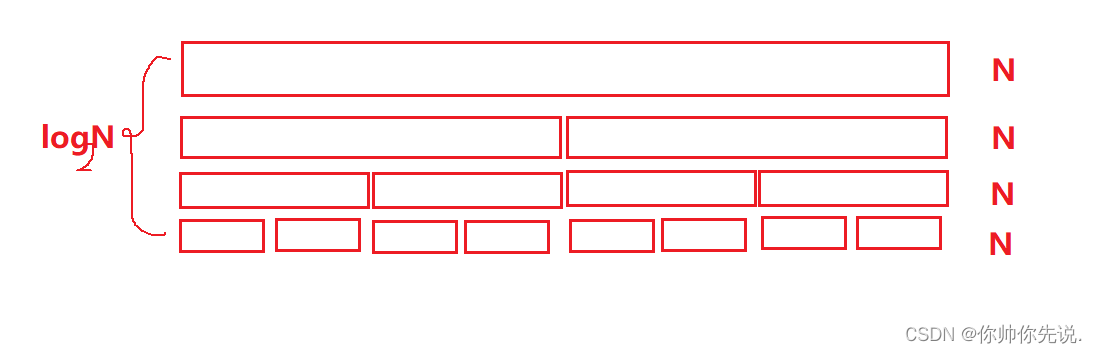
🥌快排的缺陷:
1.如果遇到有序的情况,快排的时间复杂度为O(
N
2
N^{2}
N2)

这种情况递归深度太深,会导致栈溢出,造成这种情况的原因是key值的选取不好,针对这种情况我们可以采用三数取中的方法来取key的值。
int GetMidIndex(int* a,int left,int right)
{
int mid = left + (right-left)/2;
if(a[left] < a[mid])
{
if(a[mid] < a[right])
{
return mid;
}
else if(a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
else
{
if(a[mid] > a[right])
{
return mid;
}
else if(a[left] < a[right])
{
return left;
}
else
{
return right;
}
}
}
写完这个我们就可以把原来的代码给完善了。
int Partion(int* a,int left,int right)
{
int mini = GetMidIndex(a,left,right);
Swap(&a[mini],&a[left]);
int keyi = left;
while(left <= right)
{
//右边先走,找小
while(a[right] >= a[keyi])
{
right--;
}
//左边再走,找大
while(a[left] <= a[keyi])
{
left++;
}
Swap(&a[left],&a[right]);
}
Swap(&a[left],&a[keyi]);
}
void QuickSort(int* a,int left,int right)
{
if(left >= right)
return;
int keyi = Partion(a,left,right);//接收key的下标值
QuickSort(a,left,keyi-1);
QuickSort(a,keyi+1,right);
}
有了三数取中的快排,它面对有序的情况也被优化了。
🧊2. 挖坑法
图解
同样地,还是R出发
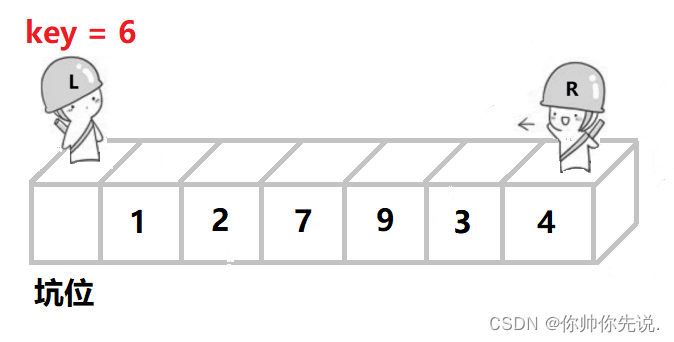
R找到比key小的值停下,把这个值扔到左边的坑位,R自己形成一个坑。
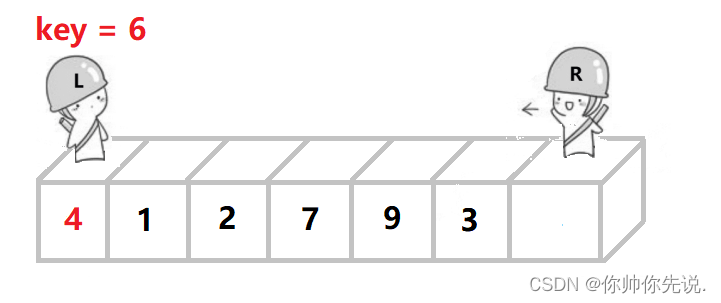
然后L开始找比key大的值,然后把这个值扔进坑位,自己形成坑
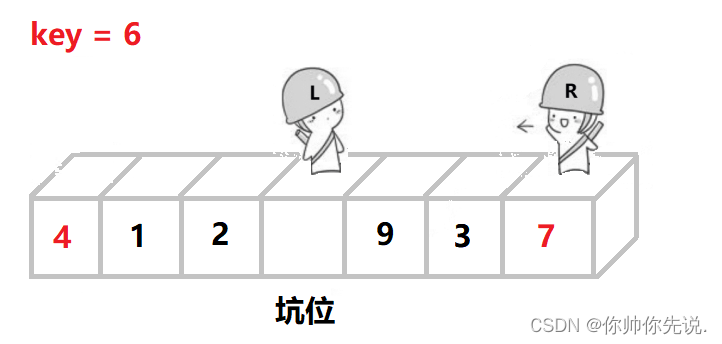
R找比key小的,然后把这个值扔进坑位,自己形成坑
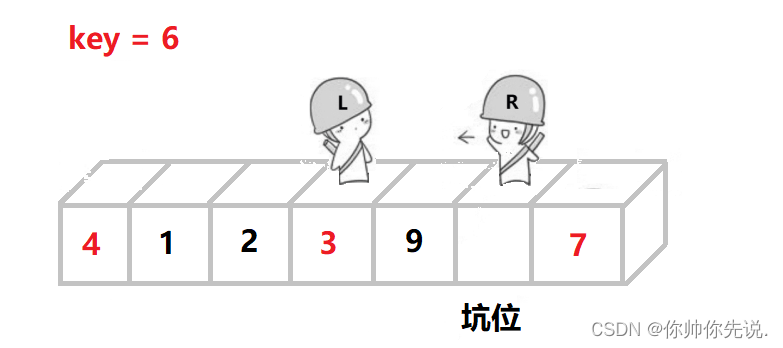
L找比key大的,然后把这个值扔进坑位,自己形成坑
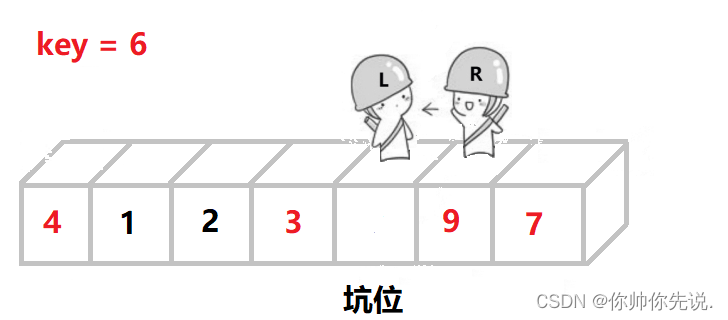
R找比key小的,与L相遇。用key把相遇时的坑给填上
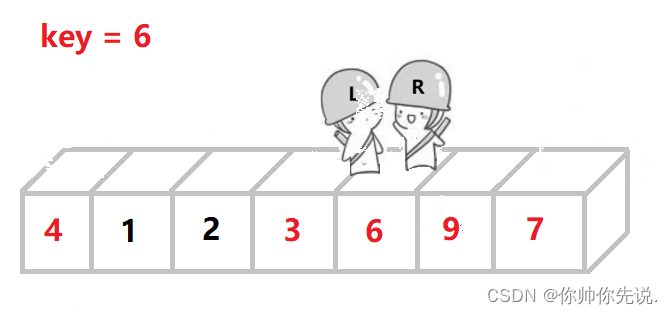
int Partion2(int* a,int left,int right)
{
int mini = GetMidIndex(a,left,right);
Swap(&a[mini],&a[left]);
int key = a[left];
int pivot = left;
while(left < right)
{
//右边找小,放到左边的坑里面
while(left < right && a[right] >= key)
{
right--;
}
a[pivot] = a[right];
pivot = right;
//左边找大,放到右边的坑里面
while(left < right && a[left] <= key)
{
left++;
}
a[pivot] = a[left];
}
a[pivot] = key;
return pivot;
}
🏒3. 前后指针法
图解
初始prev和key的位置一样,cur在key后面,cur开始找比key值小的数
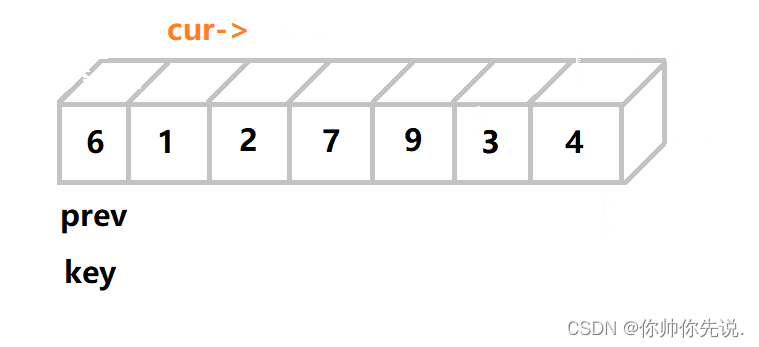
找到以后,prev++,prve和cur的值进行交换
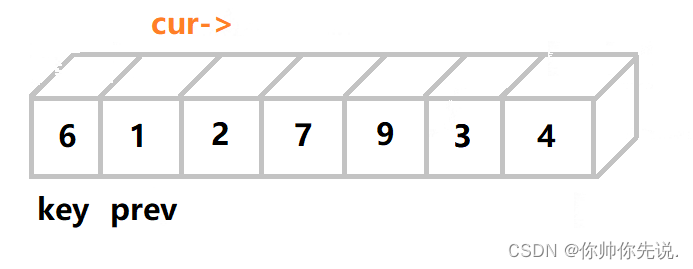
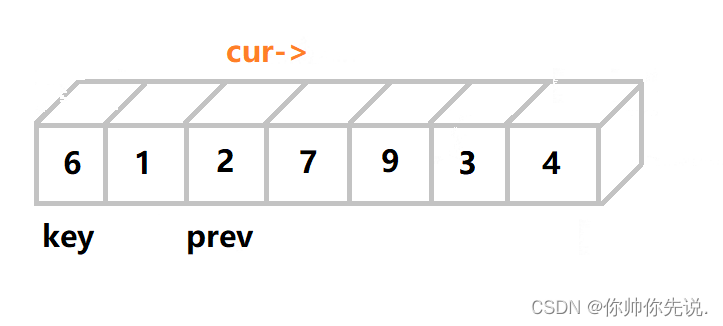
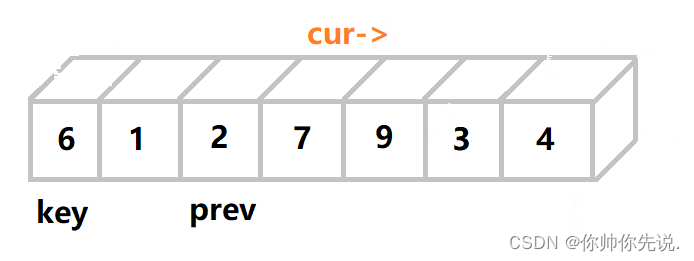
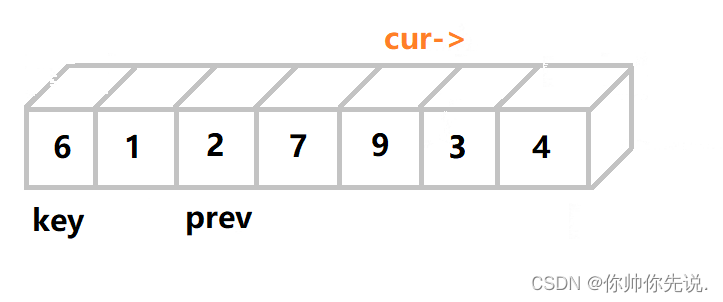
直到他们不同步时交换才真正开始
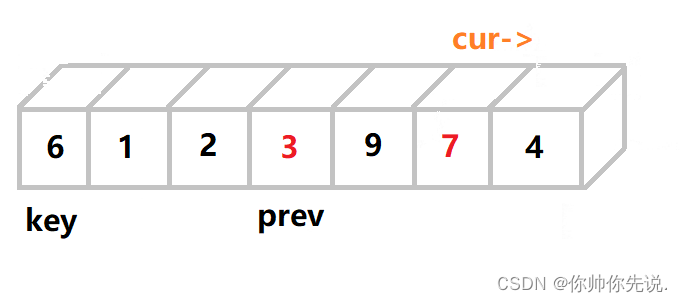
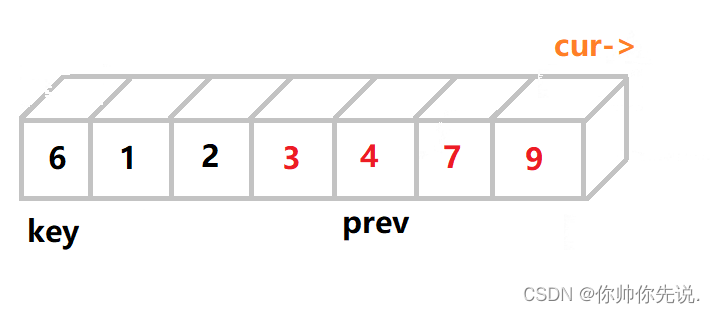
此时cur已经走到尽头了,将key的值和prev的值进行交换
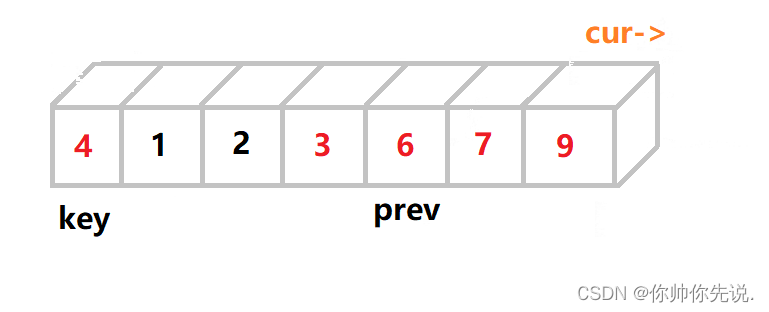
此时key的左边都比key小,key的右边都比key大。
int Partion3(int* a, int left, int right)
{
int mini = GetMidIndex(a,left,right);
Swap(&a[mini],&a[left]);
int keyi = left;
int prev = left;
int cur = prev + 1;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev!=cur)
{
Swap(&a[cur],&a[prev]);
}
cur++;
}
Swap(&a[prev], &a[keyi]);
return prev;
}
快速排序到这里还没完,我们还可以再进行优化。
我们可以对快速排序进行一个小区间优化,当分割到小区间时,不再用递归分割思路让这段子区间有序
void QuickSort(int* a,int left,int right)
{
if(left >= right)
return;
if(right-left+1<10)
{
InsertSort(a+left,right-left+1);
}
else
{
int keyi = Partion(a,left,right);//接收key的下标值
QuickSort(a,left,keyi-1);
QuickSort(a,keyi+1,right);
}
}
快排到这里实际上已经优化的非常好了,但是面对非常庞大的数据时,可能会导致栈溢出。所以我们得把快排改成非递归的模式才能更好处理庞大的数据。
我们可以考虑用栈来模拟实现递归这个过程。
void QuickSortNonR(int* a, int left, int right)
{
ST st;
StackInit(&st);
StackPush(&st, left);
StackPush(&st, right);
while (!StackEmpty(&st))
{
int end = StackTop(&st);
StackPop(&st);
int begin = StackTop(&st);
StackPop(&st);
int keyi = Partion3(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
if (keyi + 1 < end)
{
StackPush(&st, keyi+1);
StackPush(&st, end);
}
if (begin < keyi-1)
{
StackPush(&st, begin);
StackPush(&st, keyi-1);
}
}
StackDestroy(&st);
}
??????????????????
觉得写的不错可以给个一键三连 点赞👍关注💡收藏💖
??????????????????