[数据结构与算法]Floyd复盘

Floyd本身基于动态规划思想，省去一维状态形成的,算法本身只有三行，但是题目难度都比较高，需要深刻的理解

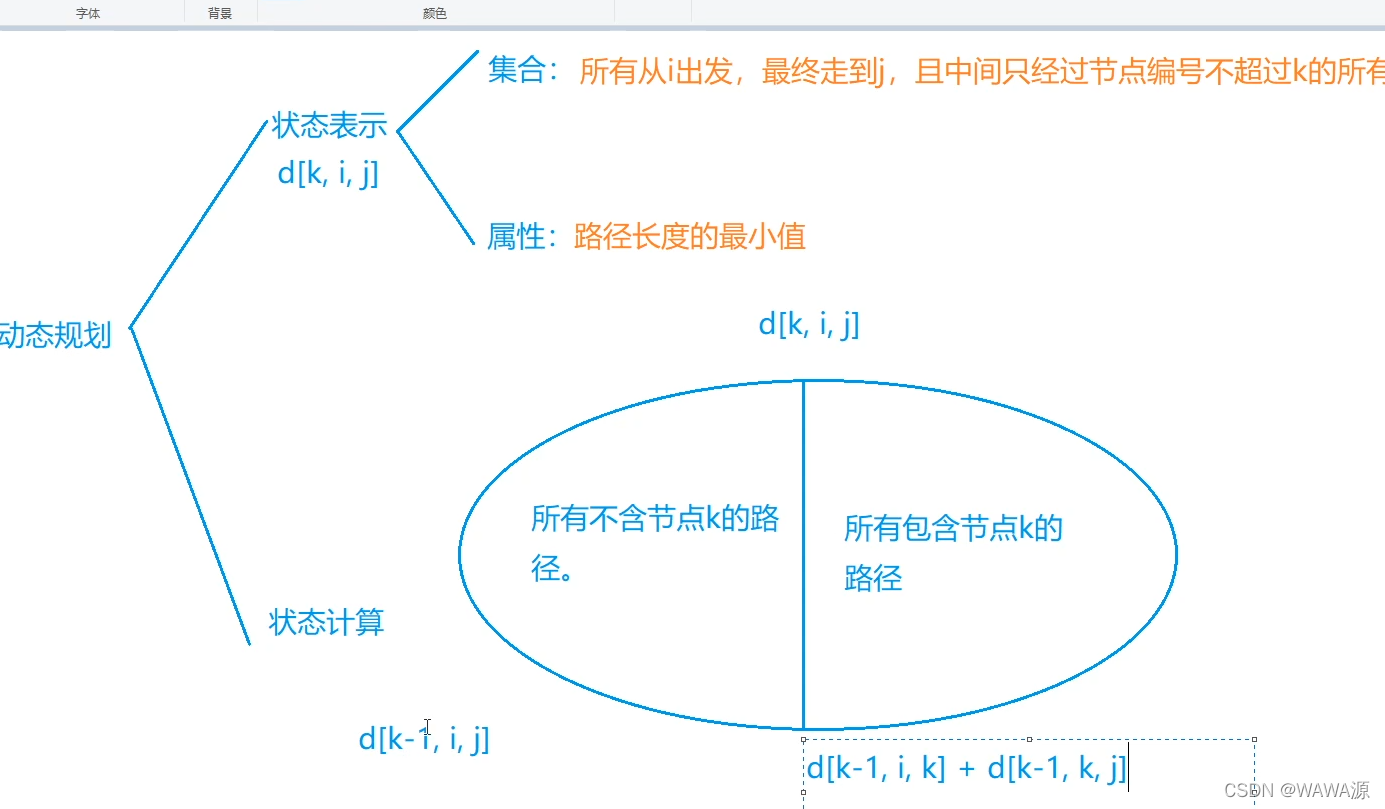
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);

1.最短路

牛的旅行

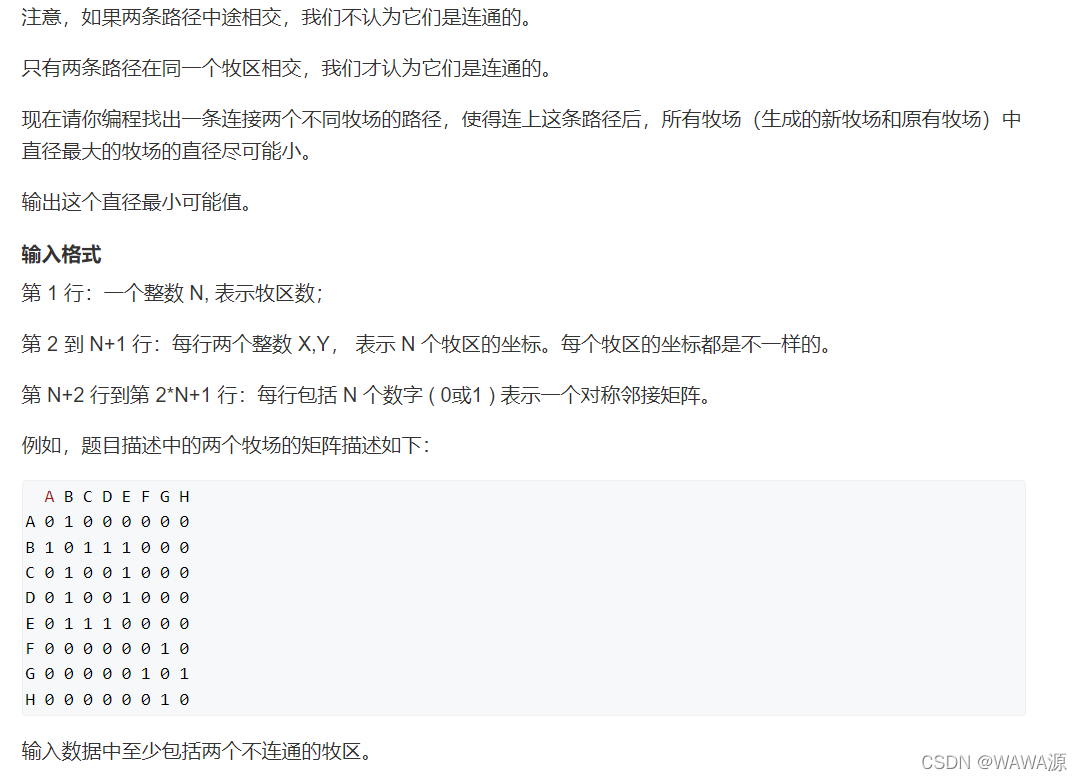
这题是Floyd的经典应用，需要注意的是分类讨论的情况

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>

using namespace std;
#define x first
#define y second
typedef pair<double, double> PDD;
const int N = 155;
const double INF = 1e18;
PDD  q[N*N];
double d[N][N];
int n;
char g[N][N];
double maxd[N];
double get_dist(PDD a,PDD b)
{
    double x=a.x-b.x;
    double y=a.y-b.y;
    return sqrt(x*x+y*y);
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)cin>>q[i].x>>q[i].y;
    for(int i=1;i<=n;i++)cin>>g[i]+1 ;
    
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(i==j)d[i][j]=0;
            else if(g[i][j]=='1')d[i][j]=get_dist(q[i],q[j]);
            else d[i][j]=INF;
        }
    }
    
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
    
    double res1=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(d[i][j]<INF/2)maxd[i]=max(maxd[i],d[i][j]);
        }
        res1=max(res1,maxd[i]);
    }
    double res2=INF;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(d[i][j]>INF/2)
            res2=min(res2,maxd[i]+maxd[j]+get_dist(q[i],q[j]));
        }
    }
    printf("%.6lf\n",max(res2,res1));
}

2.传递闭包

排序

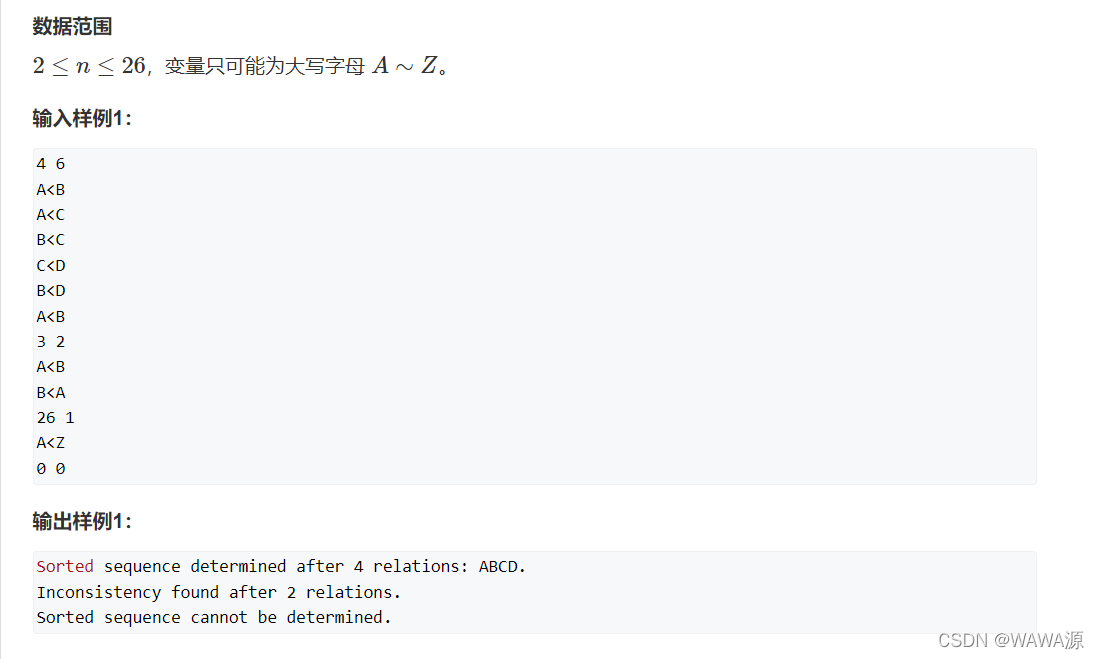
类似于差分约束，每次进入一个边的时候就跑一遍Floyd，更新状态，看是否满足要求

#include <iostream>
#include <cstring>
#include <algorithm>
#include<cstdio>
using namespace std;
const int N = 26;
int n,m;
bool g[N][N],d[N][N];
bool st[N];
void floyd(){
    memcpy(d,g,sizeof d);
    for(int k=0;k<n;k++)
       for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
           d[i][j]|=d[i][k]&&d[k][j];
}
int check(){
    for(int i=0;i<n;i++)
       if(d[i][i])
         return 2;
    for(int i=0;i<n;i++)
       for(int j=0;j<i;j++)
          if(!d[i][j]&&!d[j][i])
             return 0;
    return 1;
}
char get_min(){
    for(int i=0;i<n;i++)
        if(!st[i]){
            bool flag=true;
            for(int j=0;j<n;j++)
               if(!st[j]&&d[j][i]){
                   flag=false;
                   break;
               }
            if(flag){
                st[i]=true;
                return 'A'+i;
            }
        }
}
int main()
{
    while(cin>>n>>m,n||m){
        memset(g,0,sizeof g);
        int type=0,t;
        for(int i=1;i<=m;i++){
            char str[5];
            cin>>str;
            int a=str[0]-'A',b=str[2]-'A';
            if(!type){
                g[a][b]=1;
                floyd();
                type=check();
                if(type)t=i;
            }
        }
        if(!type)puts("Sorted sequence cannot be determined.");
        else if(type==2)printf("Inconsistency found after %d relations.\n", t);
        else {
            memset(st, 0, sizeof st);
            printf("Sorted sequence determined after %d relations: ", t);
            for(int i=0;i<n;i++)printf("%c",get_min());
            printf(".\n");
        }
    }
}

3.找最小环

观光之旅

这题就比较有难度了
摘自：Pr

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110,INF = 0x3f3f3f3f;
int g[N][N];
int n,m;
int d[N][N];
int path[N],cnt=0;
int pos[N][N];
void get_path(int i,int j){
    if(pos[i][j]==0)return ;
    int k=pos[i][j];
    get_path(i,k);
    path[cnt++]=k;
    get_path(k,j);
}
signed main()
{
    cin>>n>>m;
    memset(g,0x3f,sizeof g);
    for(int i=1;i<=n;i++)g[i][i]=0;
    for(int i=1;i<=m;i++)
    {
        int a,b,w;
        cin>>a>>b>>w;
        g[a][b]=g[b][a]=min(g[a][b],w);
    }
    memcpy(d,g,sizeof d);
    int res=INF;
    for(int k=1;k<=n;k++)
    {
        for(int i=1;i<k;i++)
            for(int j=i+1;j<k;j++)
                if((long long)d[i][j]+g[j][k]+g[k][i]<res)
                {
                    cnt=0;
                    res=d[i][j]+g[j][k]+g[k][i];
                    path[cnt++]=i;
                    get_path(i,j);
                    path[cnt++]=j;
                    path[cnt++]=k;
                }
        
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(d[i][j]>d[i][k]+d[k][j])
                {
                    d[i][j]=d[i][k]+d[k][j];
                    pos[i][j]=k;
                }
    }
    
    if(res==INF)puts("No solution.");
    else {
        for(int i=0;i<cnt;i++)cout<<path[i]<<" ";
        cout<<endl;
    }
}

4.恰好经过k条边的最短路（类floyd算法）

牛站

#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
const int N = 110;
int n,m,k,S,E;
int g[N][N];
map<int,int>ids;
int res[N][N];
void mul(int a[][N],int b[][N],int c[][N])
{
    static int tmp[N][N];
    memset(tmp,0x3f,sizeof tmp);
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                tmp[i][j]=min(tmp[i][j],b[i][k]+c[k][j]);
    memcpy(a,tmp,sizeof tmp);
}
void qmi()
{
    memset(res,0x3f,sizeof res);
    for(int i=1;i<=n;i++)res[i][i]=0;
    while(k)
    {
        if(k&1)mul(res,res,g);
        mul(g,g,g);
        k>>=1;
    }
}
signed main()
{
    cin>>k>>m>>S>>E;
    memset(g,0x3f,sizeof g);
    if(!ids.count(S))ids[S]=++n;
    if(!ids.count(E))ids[E]=++n;
    S=ids[S],E=ids[E];
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>c>>a>>b;
        if(!ids.count(a))ids[a]=++n;
        if(!ids.count(b))ids[b]=++n;
        a=ids[a],b=ids[b];
        g[a][b]=g[b][a]=min(g[a][b],c);
    }
    qmi();
    cout<<res[S][E]<<endl;
    
}