1. 稳定性
两个相等的数据,如果经过排序后,排序算法能保证其相对位置不发生变化,则我们称该算法是具备稳定性的排序算法。
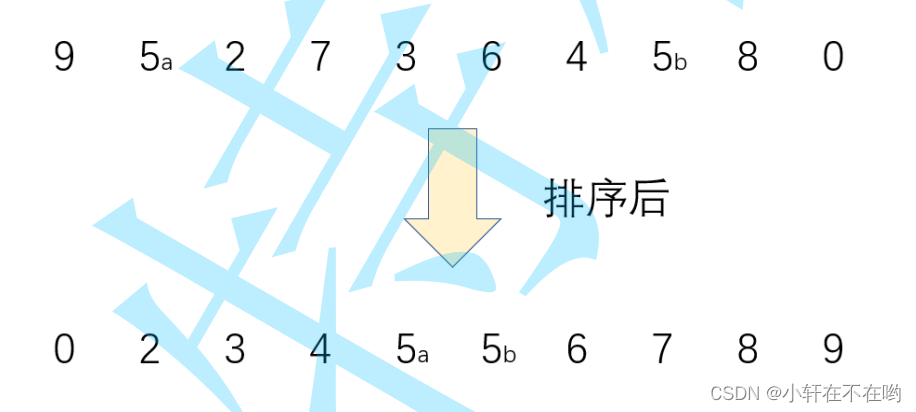
图中排序后a仍然在b前面,此时这个排序就是稳定的。
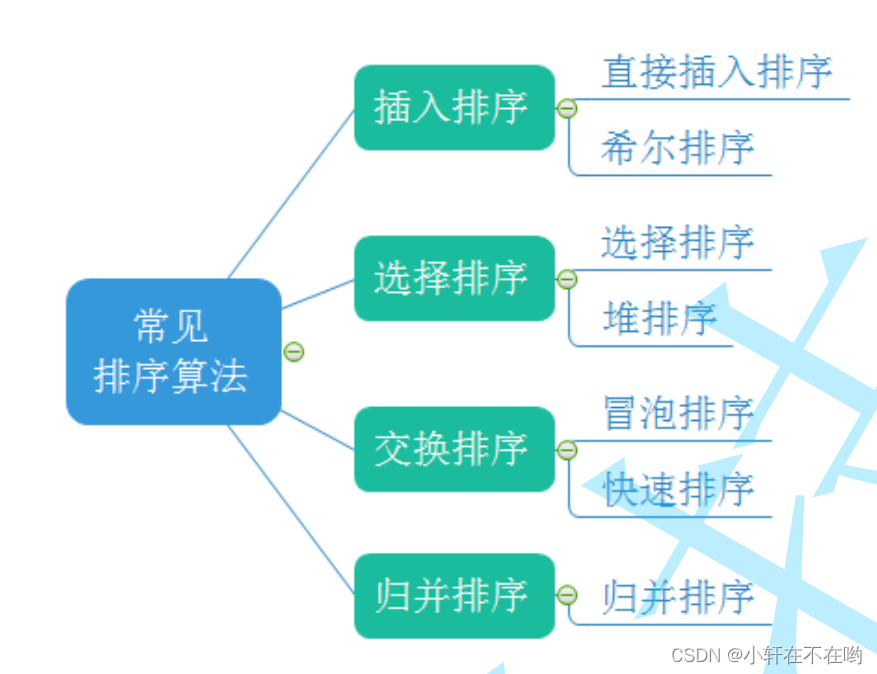
常见的排序算法有 :
2 . 插入排序
步骤:
- 从第一个元素开始,该元素可以认为已经被排序
- 取下一个元素下标定义为i,并且放到变量tmp中,从已排序的元素序列从后往前扫描
- 如果该元素大于tem,则将该元素移到下一位
- 重复步骤3,直到找到已排序元素中小于等于tem的元素,直接break
- tem插入到该元素的后面(array[j+1]=tmp;),如果已排序所有元素都大于tem,则将tem插入到下标为0的位置
- 重复步骤2~5
/**
* 直接插入排序
* 时间复杂度:O(N^2) 逆序的时候
* (最好的情况是O(N):对于直接插入排序来说,最好的情况就是数组有序的时候)
* 根据这个结论:推导出另一个结论:对于直接插入排序来说,数据越有序,越快
* 直接插入排序所以也用于其他排序的优化!
* 空间复杂度:O(1)
* 稳定性:稳定
* 一个稳定的排序,可以实现一个不稳定的排序
* 但是一个本身就不稳定的排序就不可以变成稳定的排序
* 经常使用在 数据量不多 且 整体数据趋于有序了
* @param array
*/
public void insertSort(int[] array){
for (int i =1 ; i <array.length ; i++) {
int tmp=array[i];
int j=i-1;
for (; j>=0 ; j--) {
if (array[j]>tmp){
array[j+1]=array[j];
}else {
// 只要j回退的时候,遇到了比tmp小的元素,就结束这次的比较
break;
}
}
//j回退到了 小于0 的地方
array[j+1]=tmp;
}
}
动图演示如下:
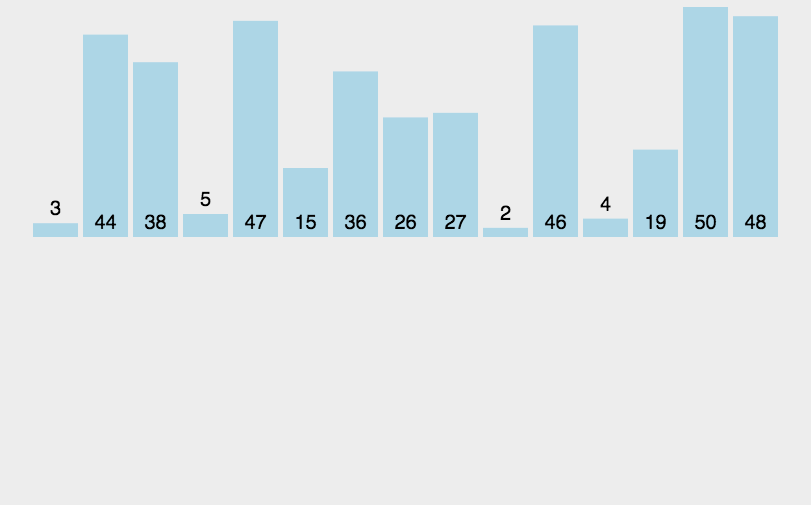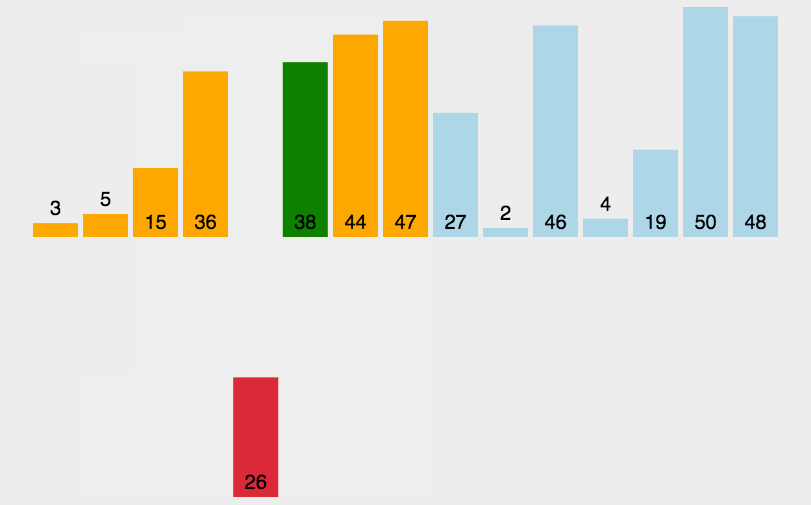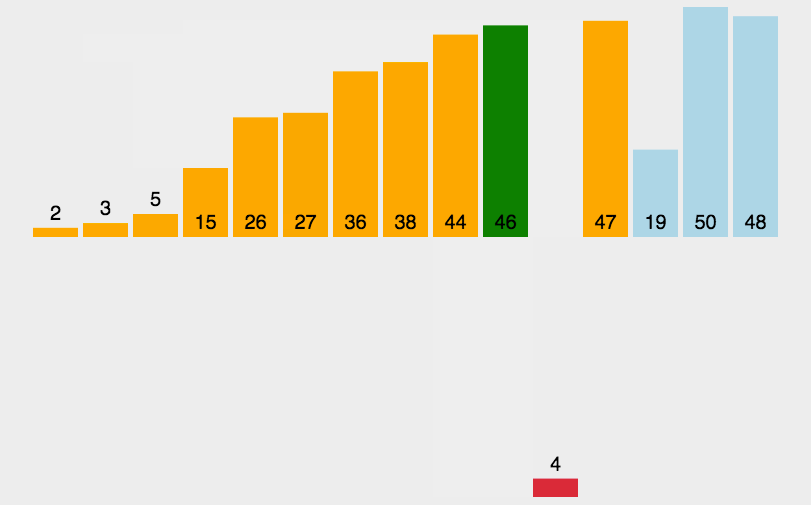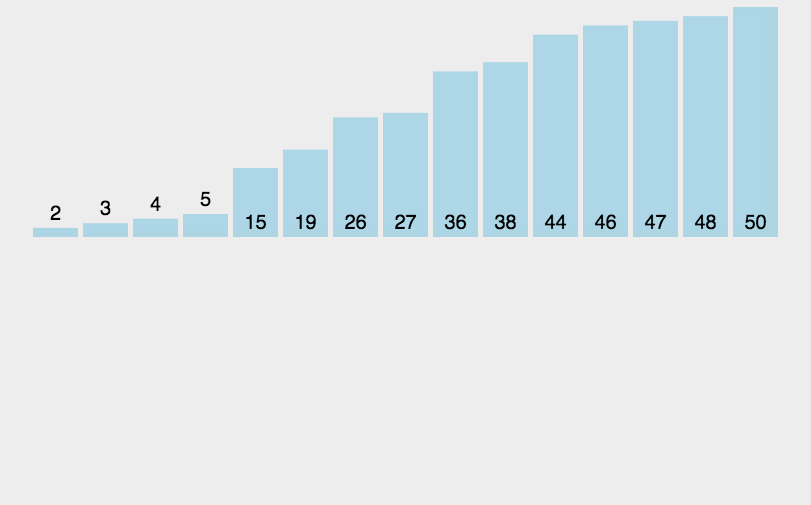
3. 希尔排序
步骤:
- 先选定一个小于N的整数gap作为第一增量,然后将所有距离为gap的元素分在同一组,并对每一组的元素进行直接插入排序。然后再取一个比第一增量小的整数作为第二增量,重复上述操作…
- 当增量的大小减到1时,就相当于整个序列被分到一组,进行一次直接插入排序,排序完成。
/**
* 希尔排序
* 时间复杂度:O(N^1.3-N^1.5)
* 空间复杂度:O(1)
* 稳定性 : 不稳定的
* 看在比较的过程当中,是否发生了跳跃式的交换,如果发生了跳跃式的交换 那么就是不稳定的排序
* (基本上没有考过)
*
* @param array
* @param gap 组数
*/
public static void shell(int[] array,int gap){
for (int i =gap ; i <array.length ; i++) {
int tmp=array[i];
int j=i-gap;
for (; j>=0 ; j-=gap) {
if (array[j]>tmp){
array[j+gap]=array[j];
}else {
// 只要j回退的时候,遇到了比tmp小的元素,就结束这次的比较
break;
}
}
//j回退到了 小于0 的地方
array[j+gap]=tmp;
}
}
public static void shellSort(int[] array){
int gap=array.length;
while (gap>1){
shell(array,gap);
gap/=2;
}
shell(array,1);
}
动图演示如下:
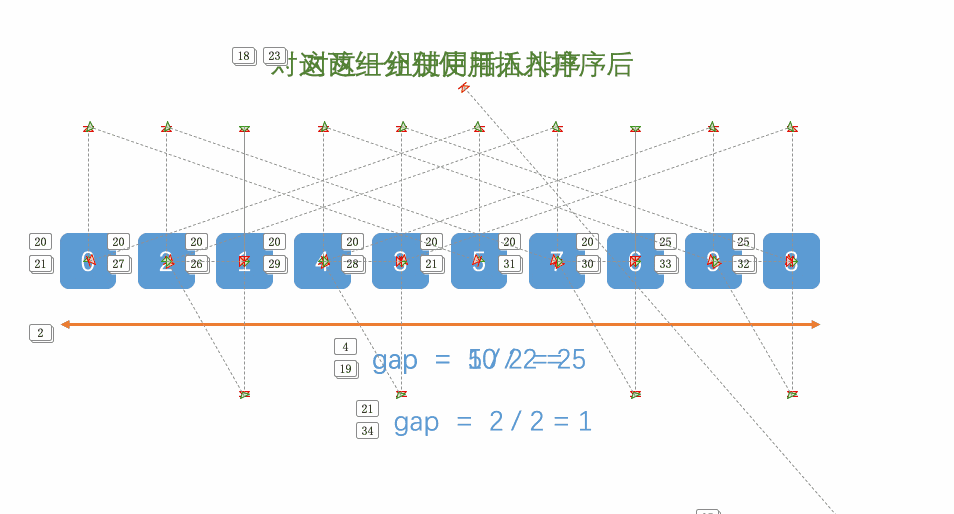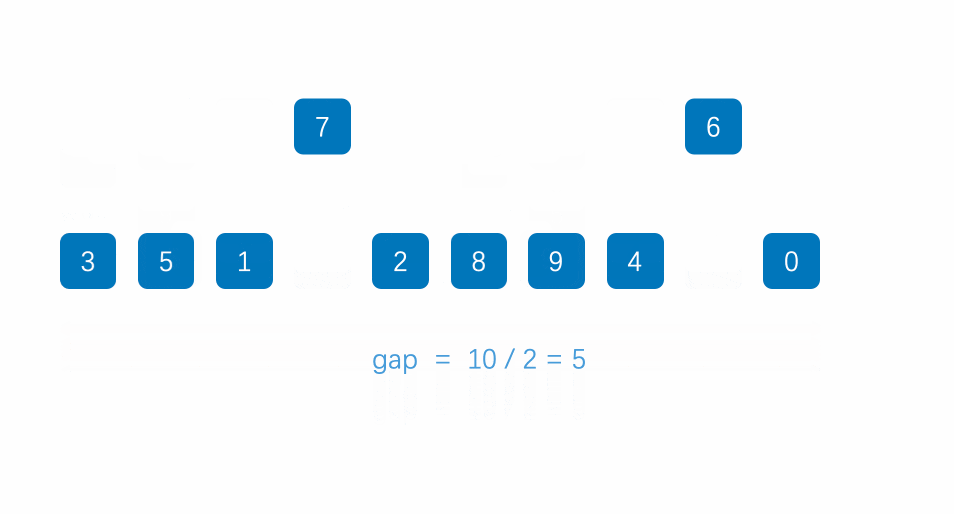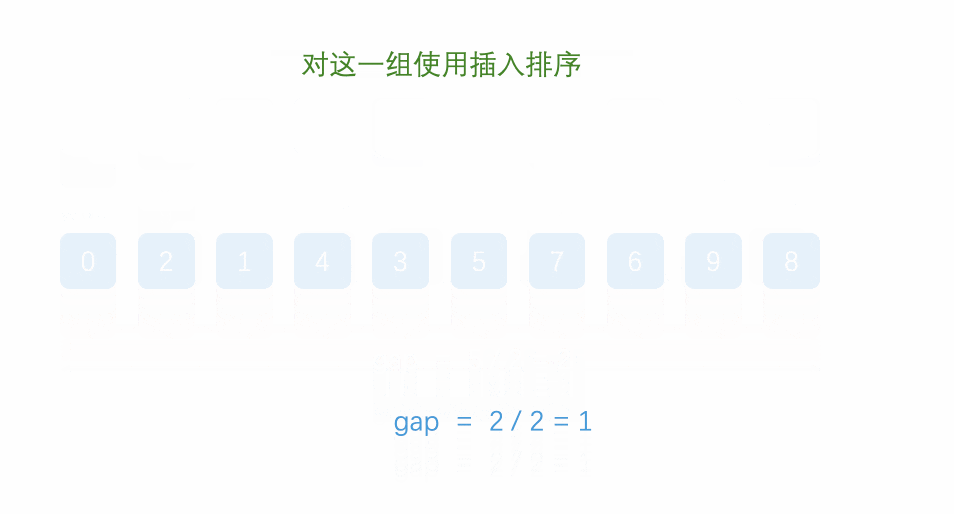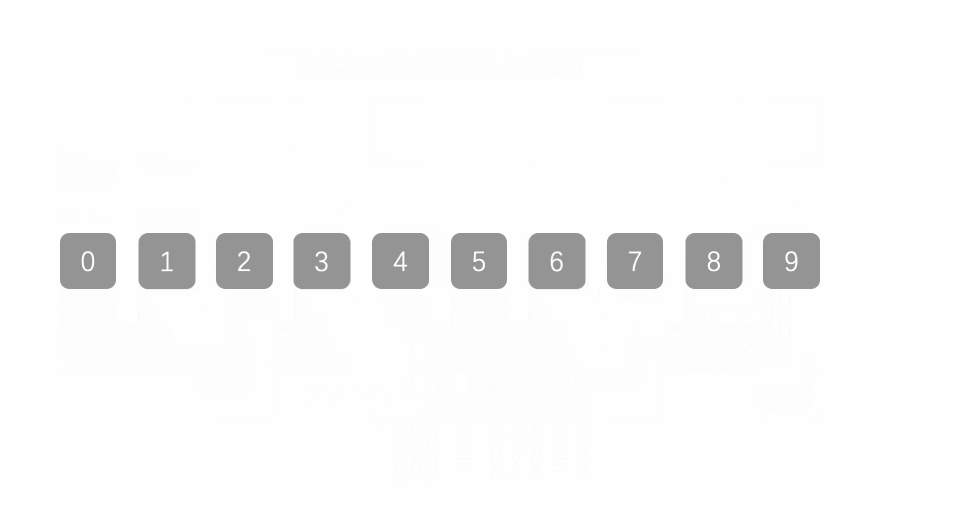
4. 选择排序
思路:
每次从待排序列中选出一个最小值,然后放在序列的起始位置,直到全部待排数据排完即可。
实际上,我们可以一趟选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。
/**
* 选择排序
* 时间复杂度:O(N^2)
* 空间复杂度:O(1)
* 稳定性:不稳定的排序
* @param array
*/
public static void swap(int[] array,int i,int j){
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}
//优化选择排序:每次交换都是当前遍历j时候的最小值
public static void selectSort1(int[] array){
for (int i = 0; i < array.length; i++) {
int minIndex=i;
for (int j = i+1; j < array.length ; j++) {
if (array[j]<array[minIndex]){
minIndex=j;
}
}
swap(array,i,minIndex);
}
}
public static void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
for (int j = i + 1; j < array.length; j++) {
if (array[i] > array[j]) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
}
}
}
动图演示如下 :
5. 堆排序
基本原理也是选择排序,只是不在使用遍历的方式查找无序区间的最大的数,而是通过堆来选择无序区间的最大的数。
注意: 排升序要建大堆;排降序要建小堆。
堆排序可以参考之前写的一篇博文:堆详解
也可以借鉴大佬的一篇关于堆排的文章,博主看了受益匪浅:堆排序
/**
* 堆排序 排升序要建大堆;排降序要建小堆。
* 时间复杂度 :O(N*logN)
* 空间复杂度 : O(1)
* 稳定性:不稳定的
*
* @param array
*/
public static void heapSort(int[] array){
//1.建堆 O(N)
creatHeap(array);
int end=array.length-1;
//2.交换然后向下调整为大根堆 O(N*logN)
while (end>0){
swap(array,0,end);
shiftDown(array,0,end);
end--;
}
}
public static void creatHeap(int[] array){
for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {
shiftDown(array,parent,array.length);
}
}
public static void shiftDown(int[] array,int parent,int len){
int child=2*parent+1; //左孩子
while (child<len){
if (child+1<len && array[child]<array[child+1]){
child++; //保证child下标,就是左右孩子最大值下标
}
if (array[child]>array[parent]){
swap(array,child,parent);
parent=child;
child=2*parent+1;
}else {
break;
}
}
}
算法图解 :

6 冒泡排序
原理:
在无序区间,通过相邻数的比较,将最大的数冒泡到无序区间的最后,持续这个过程,直到数组整体有序
思路:
排序一趟可以让最大的数字沉底
排序len-1趟,一趟排序len-1-i次
详细实现看代码
/**
* 冒泡排序(未优化)
* 时间复杂度:O(N^2)
* 空间复杂度:O(1)
* 稳定性:稳定的排序
* @param array
*/
public static void bubbleSort(int[] array){
for (int i = 0; i < array.length-1; i++) {
for (int j = 0; j < array.length-1; j++) {
if (array[j]>array[j+1]){
swap(array,j,j+1);
}
}
}
}
/**
* 冒泡排序(优化)
* 时间复杂度:O(N^2) (最坏的情况)
* (最好的情况 : 有序) O(N)
* 空间复杂度:O(1)
* 稳定性:稳定的排序
* @param array
*/
public static void bubbleSort2(int[] array){
for (int i = 0; i < array.length-1; i++) {
boolean flg=false;
for (int j = 0; j < array.length-1-i; j++) {
if (array[j]>array[j+1]){
swap(array,j,j+1);
flg=true;
}
}
if (flg==false){ //没交换的话说明flg没被制成TRUE,则说明已经有序,可以跳出循环了
break;
}
}
}
动图演示如下 :