基础概念
配置空间、工作空间
- 机器人配置(Robot Configuration):对机器人上所有点的位姿描述
- 机器人自由度(Robot Degree Of Freedom, DOF):描述机器人路径规划的最少坐标数量 n n n。
- 机器人配置空间(Robot Configuration Space, C-Space):包含机器人所有可能位姿的 n n n维空间
- 机器人位姿在配置空间中假定为一个点
- 机器人工作空间(Robot Workspace):机器人实际工作的复杂环境
障碍物、运动规划
机器人具有不同的形状、尺寸大小,障碍物(Obstacle)的碰撞检测需要了解机器人的形状、大小等属性,较为复杂:
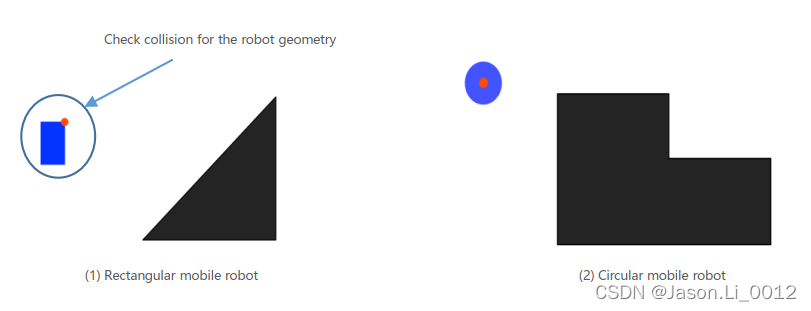
故而,一般在配置空间中做机器人的路径规划问题。已知机器人位姿在配置空间C-space中假定为一个点,例如欧氏空间下的机器人位姿可使用 ? 3 × 3 ∈ S O ( 3 ) \Re^{3\times3}\in SO(3) ?3×3∈SO(3)进行表示。则可将障碍物进行膨胀得到配置空间中的障碍物(C-Obstacle),若机器人所在点不落在C-Obstacle范围内,则判定机器人处于自由状态下,不会被碰撞:C-Free。
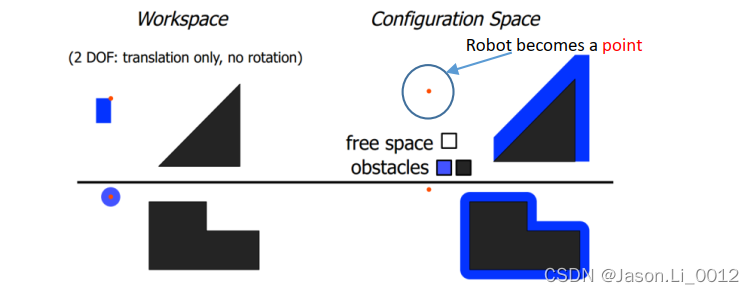
配置空间由障碍物及自由空间组成: ( C ? S p a c e ) = ( C ? O b s t a c l e ) ∪ ( C ? F r e e ) (C-Space)=(C-Obstacle)\cup(C-Free) (C?Space)=(C?Obstacle)∪(C?Free)
移动机器人的运动规划是在机器人的起点 q s t a r t q_{start} qstart?到机器人的目标点 q g o a l q_{goal} qgoal?之间,处于 C ? F r e e C-Free C?Free空间中的规划。
图搜索(Graph Search Basis)
图(Graphs)
图是一种由节点(Nodes)和边(Edges)构成的抽象网络,网络中各个节点由边进行连接,表明两节点存在关系。
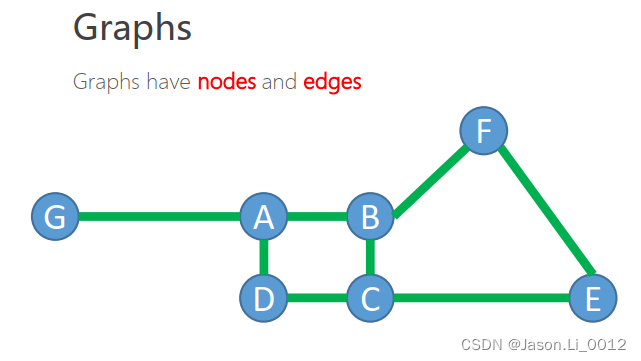
节点(Node)
节点表示某个事物或对象,如上图中各个带字母的点。
边(Edge)
边表示事物与事物间的逻辑关系,如上图中两节点间的绿线。
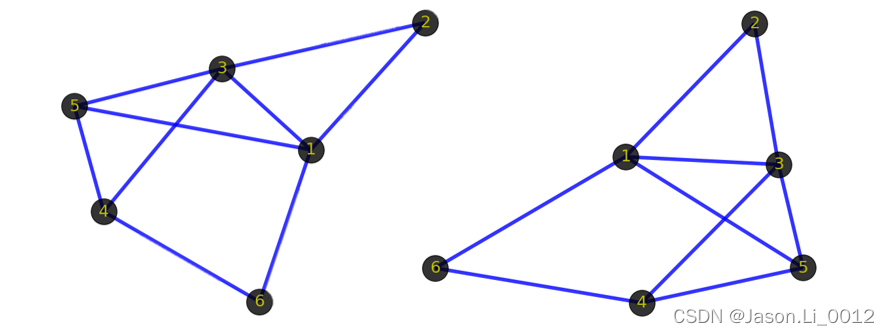
同构(Isomorphism)
同构的两张图具有相同的节点及节点间连接的边,同构图仅存在画法的不同,但包含的逻辑关系不变。
有向图(Directed Graph)、无向图(Undirected Graph)
无向图的边没有方向,而有向图的边具有方向性。
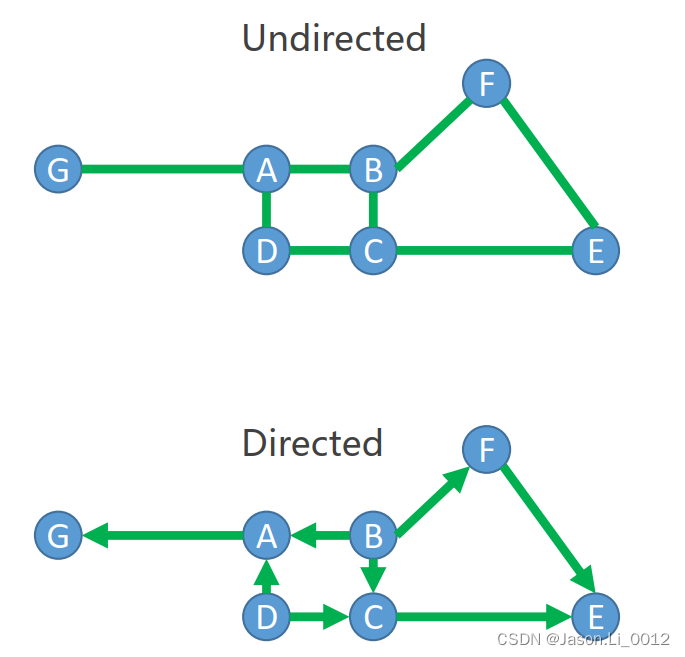
如上图,有向图的方向如下: D → A → G D\to A\to G D→A→G、 D → C → E D\to C\to E D→C→E、 B → A → G B\to A\to G B→A→G、 B → C → E B\to C\to E B→C→E、 B → F → E B\to F\to E B→F→E
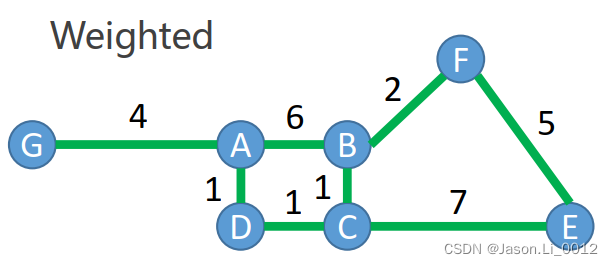
权重(Weight)
图上的边具有权重值,每条边的权重可以不同,表示由一个节点至另一个节点的代价值。如下图由节点 A A A到节点 G G G的权重值为4。
路径(Path)、最优路径(Shortest Path)
图上任取两点作为起点与目标点,由起点到目标点,不经过重复节点和边的路线称为路径。由起点到目标点最短的路径称为最优路径,在选择最优路径时往往需要考虑边的权值。
图搜索(Search-based Method )
对图结构进行搜索,从起始节点 S S S到目标节点 G G G,将生成一个搜索树:
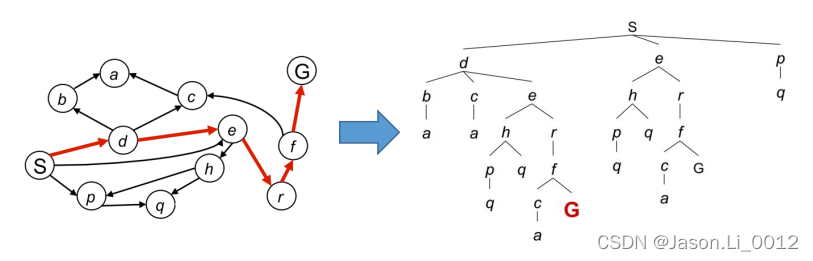
通常,构建一个完整的搜索树结构,所需要的代价很高。图搜索算法的基本逻辑如下:
1
:
维
护
一
个
用
于
存
储
所
有
被
访
问
节
点
的
容
器
2
:
容
器
内
初
始
值
为
起
点
X
s
3
:
开
始
循
环
L
o
o
p
4
:
访
问
节
点
:
根
据
预
先
定
义
的
评
分
函
数
(
S
c
o
r
e
?
F
u
n
c
t
i
o
n
)
从
容
器
中
取
出
一
个
节
点
5
:
扩
展
节
点
:
获
得
该
节
点
的
所
有
邻
居
节
点
6
:
置
入
节
点
:
将
获
得
的
邻
居
节
点
置
入
容
器
7
:
结
束
循
环
E
n
d
\begin{aligned} &1:维护一个用于存储所有被访问节点的容器\\ &2:容器内初始值为起点X_s\\ &3:开始循环Loop\\ &4:\qquad访问节点:根据预先定义的评分函数(Score\:Function)从容器中取出一个节点\\ &5:\qquad扩展节点:获得该节点的所有邻居节点\\ &6:\qquad置入节点:将获得的邻居节点置入容器\\ &7:结束循环End \end{aligned}
?1:维护一个用于存储所有被访问节点的容器2:容器内初始值为起点Xs?3:开始循环Loop4:访问节点:根据预先定义的评分函数(ScoreFunction)从容器中取出一个节点5:扩展节点:获得该节点的所有邻居节点6:置入节点:将获得的邻居节点置入容器7:结束循环End?
循环结束条件一般置为抵达目标节点,或容器中所有节点被弹出,容器为空。
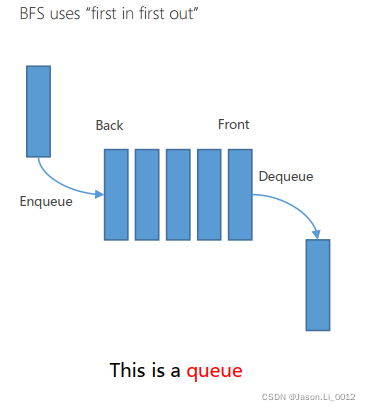
广度优先搜索(Breadth First Search, BFS)
广度优先算法基于队列(Queue)进行,遵从于先进先出的原则进行:
举例说明如下:
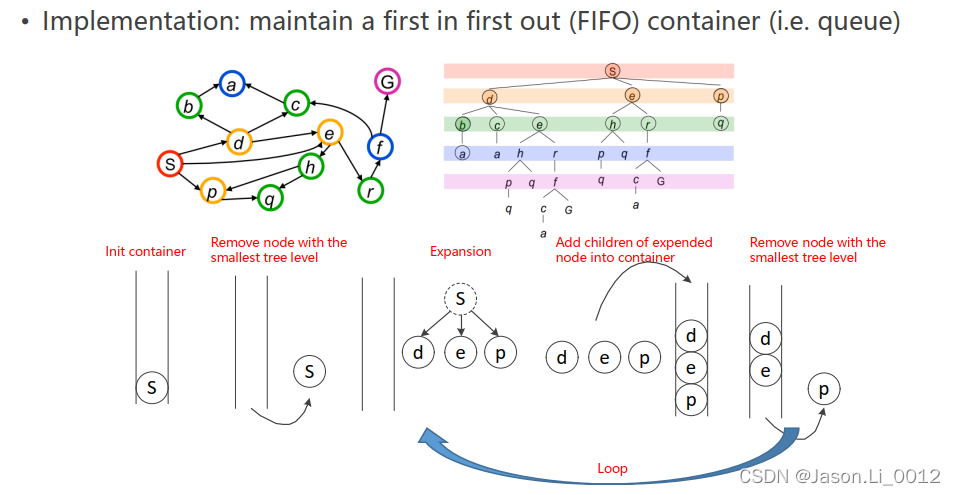
广度优先搜索搜先从起点节点 s s s开始,首先弹出节点 s s s,得到三个邻居节点 d 、 e 、 p d、e、p d、e、p并置入容器中;随后弹出其中一个节点 p p p,得到其邻居节点 q q q置入容器;其次,再弹出一个节点 e e e并将其邻居节点 h 、 r h、r h、r置入容器;周而复始,弹出 d d d并将其邻居节点 b 、 c 、 e b、c、e b、c、e置入容器……知道搜索到目标为止。
应注意,对于邻居节点置入容器的顺序需要被确立,如从左到右置入、顺时针置入等方式。
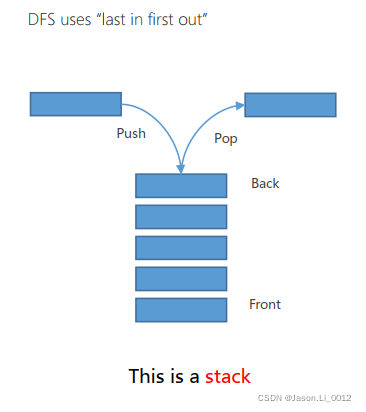
深度优先搜索(Depth First Search, DFS)
深度优先搜索基于堆栈(Stack)进行,遵从于后进先出原则进行:
举例说明如下:
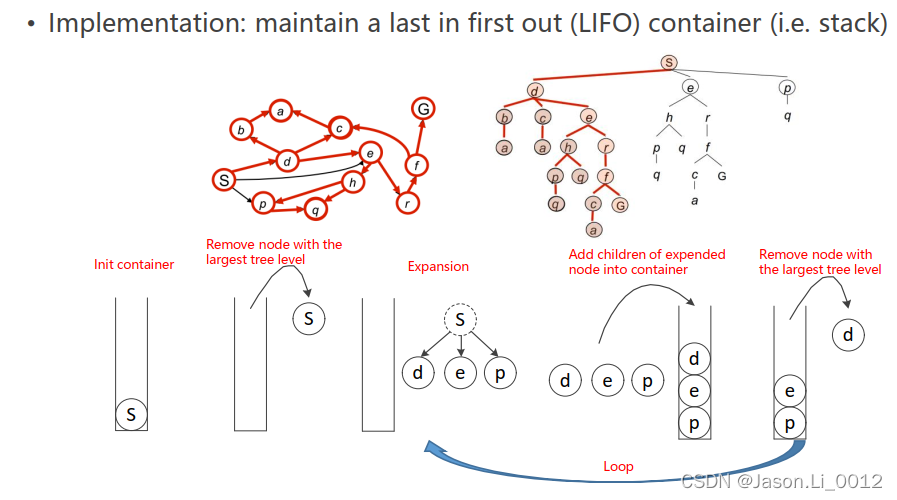
首先,从起点节点 s s s开始搜索,弹出节点 s s s后,得到邻居节点 d 、 e 、 p d、e、p d、e、p并将其置入容器;随后,弹出节点 d d d得到其邻居节点 b 、 c 、 e b、c、e b、c、e置入容器;周而复始,弹出 b b b得到邻居节点 a a a置入容器后,发现对 a a a进行搜索无邻居节点,故而再一次弹出节点 c c c得到其邻居节点 a a a,同样无邻居节点并再次弹出 e e e……直到抵达目标节点 G G G时离开循环。
同样应注意,对于邻居节点置入容器的顺序需要被确立。
效果对比
如下图所示,左侧为BFS右侧为DFS。一般深度优先搜索所得并非最短路径,故而实际在最优路径规划中,采用BFS进行:

贪心算法(Greedy Best First Search)
BFS和DFS算法弹出的下一个节点顺序按照先入先出、后入先出的规则进行,而贪心算法则通过人为指定的规则进行弹出对应节点,称为启发(heuristic)
启发(heuristic)
一个heuristic被定义为:当前点到目标点距离的猜测(Guess),此距离忽略地图中的障碍物,可采用欧氏距离(Euclidean Distance)或曼哈顿距离(Manhattan Distance)进行猜测。
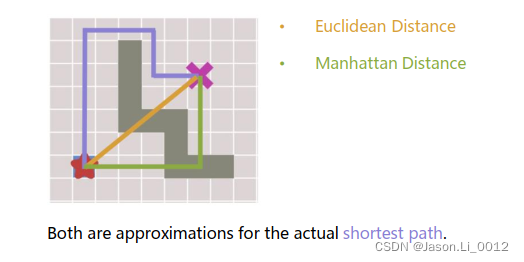
一个heuristic应该易于计算,同时它将给予我们搜索图的方向。
效果对比
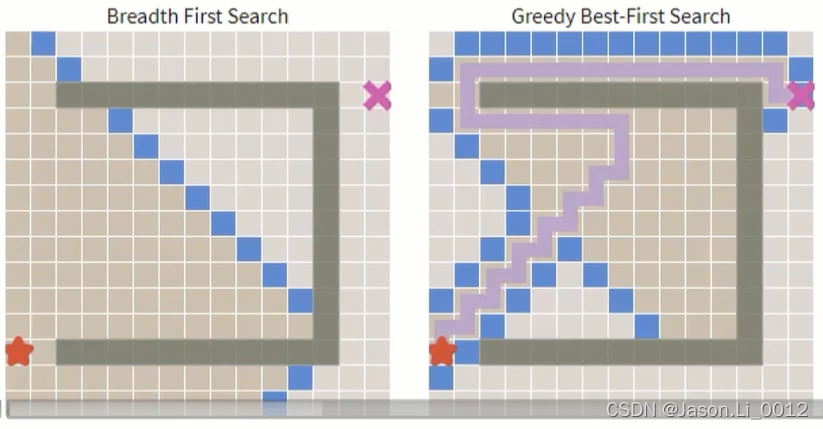
在理想环境中,不存在障碍物。与BFS算法相比,贪心算法能够在更短时间内找到最短路径(下图一)。而在效果上,两者规划得到的最优路径相同(下图二):
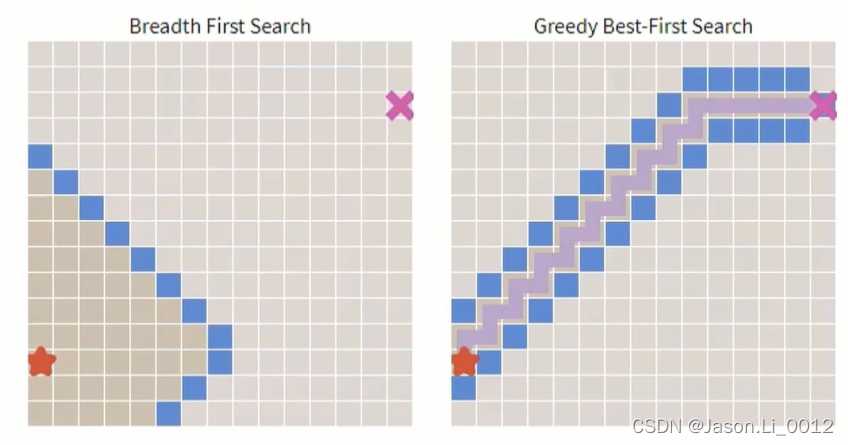

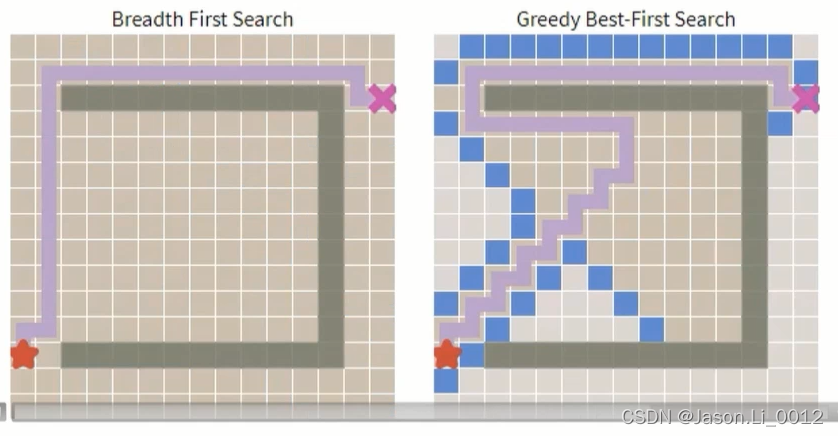
然而在实际地图环境下,存在大量的障碍物。此时,虽然贪心算法依旧能够较快得到规划路径(下图一),但是所得的路径并非实际上的最优路径(下图二):