[数据结构与算法]相位相关匹配

背景知识

复数模长计算

复数$G=A+B?i$，他的共轭即 $G^{?}=A?B?i$

我们可用复向量共轭求取模长平方：
$G?G^{?}=(A+B?i)?(A?B?i)$
. . . . . . . .$=A^2+B^2$
. . . . . . . .$={\rho }^2$

复数的共轭计算，除了用来求取模长，还用在内积、夹角求取上：$z_1?{\bar{z}}_2$

复数的另外一种写法：$Z=\rho ?e^{i\theta }$
则内积：$z_1?{\bar{z}}_2={\rho }_1{e}^{i{\theta }_1}?{\rho }_2{e}^{?i{\theta }_2}$
则夹角的度量可为为：
$\frac{z_1?{\bar{z}}_2}{|z_1||{\bar{z}}_2|}=e^{i({\theta }_1?{\theta }_2)}$

傅里叶平移不变性

首先介绍一下傅里叶变换，傅里叶变换的作用，便是将一个信号分解为正弦函数的组合。其逆变换就是将正弦函数组合，合成一个信号。对于一个确定频率为 $\omega$ 的正弦波，其有如下性质：
$sin(\omega t+\theta )=\alpha \times sin(\omega t)+\beta \times cos(\omega t)$

由中学三角函数分解公式可得： $\alpha =cos(\theta )$，$\beta =sin(\theta )$

这告诉我们一个道理，一个固定频谱的正弦函数发生平移，只会引起相位角发生变化，也就是cos和sin分量发生变化，并不会引起频谱移动。

将一个确定函数使用傅里叶变换分解为正弦函数后，由于每个正弦函数都有如上性质，所以对于一个确定函数而言，平移它并不会改变分解后的频谱幅度，只会改变其相位的角度。

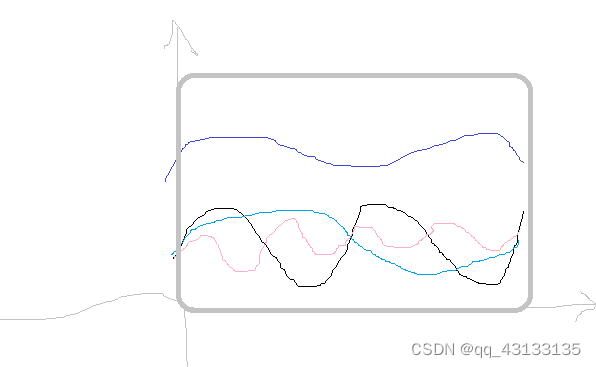
如果一个信号可以被分解为3个正弦波：

假设紫色波形由下面三个正弦信号合成，我们可以想象到，上面的信号要是向左移动了$x$，那么下面三个信号也必须同时向左移动$x$，才能合成上面那个的信号。

相位相关

如果我们要求解平移量怎么办呢，我们知道，平移后的信号，频率的幅度不会改变，只是相位改变了。假设两个频率相同的正弦信号，$f(\theta )=g(\theta +t)$，即$g(x)$是$f(x)$平移t后得到。如果我们要求偏移量t，那么只需要做信号相关计算：

t = { ? n ， . . . ， 0 ， 1 ， 2 ， . . . . ， n } t=\{-n，...，0，1，2，....，n\} t={?n，...，0，1，2，....，n}
对每个t计算内积
$f(x)?g(x?t)=f(0)?g(0?t)+f(1)?g(1?t)...$
我们知道两个向量只有方向一样时的内积才会最大，所以我们取内积$f(x)?g(x?t)$最大时，该t作为偏移量

这样一个个t试过去的办法，相对来说会慢一点，快一点的方法便是分别对两个函数求傅里叶变换，得到频域的复数表示：

$f(x):F(\omega )=A+B?i$
$f(g):G(\omega )=C+D?i$
由于他俩是同频，所以$\omega$自然是相同的了

由于这是一个复数，我们可以求得内积为：

$F(\omega )?\bar{G}(\omega )={\rho }_1{e}^{i{\theta }_1}?{\rho }_2{e}^{?i{\theta }_2}$

然后由于结果还是一个复向量，我们可以除以模长归一化一下可得：
$\frac{F(\omega )?\bar{G}(\omega )}{|F(\omega )?\bar{G}(\omega )|}=e^{i({\theta }_1?{\theta }_2)}$

现在我们已经求得偏移夹角了${\theta }_0={\theta }_1?{\theta }_2$。

$e^{i({\theta }_0)}=cos({\theta }_0)+i?sin({\theta }_0)$

此时我们只需要进行逆傅里叶变换，可得到以${\theta }_0$为起始的函数，并且对于该函数而言，取得最大值处的x便是偏移量:

$fg(x)=e^{i{\theta }_0}?e^{?i\omega x}=e^{i({\theta }_0?x)}$
根据欧拉公式知道
$e^{i({\theta }_0?x)}=cos({\theta }_0?x)+i?sin({\theta }_0?x)$

所以逆傅里叶变换可得实部：$cos({\theta }_0?x)$，在$x={\theta }_0$处取得最大值。所以取得最大值处便是偏移量${\theta }_0$

图像频谱图

对于傅里叶变换的平移不变性上面说过了，当然，你也可以使用公式严格推导下面结论：

设$f(x)$的傅里叶分解为$F(\omega )$，若$f(x)$平移了$t$
则$f(x?t)=e^{?2j\pi t}F(\omega )$

当然，图像平移不会改变频谱幅度（但是改变相位），不过图像旋转，频谱也会跟着旋转，图像旋转多少度，频谱也跟着旋转多少度：

设极坐标下，$f(r,\theta )$的傅里叶分解为$F(\omega ,?)$，若$f(r,\theta )$旋转了$t$角度
则$f(r,\theta +t)=e^{?2j\pi t}F(\omega ,?+t)$

证明太繁琐，一幅图说明如下:

对数极坐标变换

这个相对比较简单，就是从图像的中心，按极坐标展开，得到右边的方形图（横向与园半径同，纵向与与角度对应）

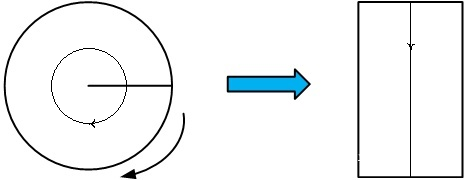
这种展开，对于频谱图的旋转分析，优势是很大的，不知道你发现没，如果原图像旋转了，那么频谱图就绕其中心旋转，我们如果转换到对数极坐标下，这种旋转就变成上下平移了。于是我们便将原图的旋转，由频谱图的旋转分析变成了 频谱图极坐标变换后的平移分析了。

功率谱

频谱是一个信号从时域表示转变为频域表示,归根结底只是同一种信号的不同的表示方式而已。 而功率谱是从能量的观点对信号进行的研究。频谱和功率谱和关系归根揭底还是信号和能量、功率等之间的关系。

对信号进行傅里叶变换后，是一个复数（A+Bi)，我们通常将其转为幅度和相位进行分析。所以频谱包含幅度谱和相位谱两个部分，而其中幅度谱的平方（二次量纲）又叫能量谱（密度），它描述了信号能量的频域分布。不过能量谱和功率谱本质上还是有些差异的。我们都知道$W=P?t$，只有当t为1时，能量和功率才会在数值上相等。

功率谱指的是信号在每个频率分量上的功率，频谱的幅度谱，只信号在各个分量上的幅度值。因为通信中一般对于信号的分析都是把信号看作电压值。所以功率就是电压的平方再除以电阻值，即$P=\frac{V^2}{R}$。在做定性分析时，为了方便起见，一般假设R为1Ω的电阻，从而得到归一化的功率谱值，这时候功率谱就是频谱模的平方了。模也就是实部分量和虚部分量平方和的开方。

互功率谱

互功率谱是在频域内描述两个不同信号之间统计相关程度的一种方法。也就是之前用到的归一化内积公式：
$\frac{F(\omega )?\bar{G}(\omega )}{|F(\omega )?\bar{G}(\omega )|}$
原理很简单，之前说过了，只要对该值进行逆傅里叶变换，就能在偏移量处取得最大值。

相位相关匹配

相位匹配

两幅图像之间有位移，可以计算其频域互功率谱，然后对其最后在对互功率谱进行ifft变换可得到一个冲击函数，此函数在其他位置几乎为零，只有在（x0,y0）处有最大值，由此可计算出平移参数。具体原理上面讲过了。

旋转匹配

在上面对数极坐标中介绍过，将一副图像进行傅里叶变换后，进行对数极坐标变换，就可以将旋转匹配变成平移匹配，而对于平移匹配则采样上面提到的互功率谱的方法进行偏移量求解，然后求得旋转参数，将傅里叶变换的图旋正，再进行一次平移变换匹配即可。

傅里叶-梅林变换

在上面的旋转匹配过程中，将频谱幅度变换到极坐标下后，垂直方向的位移代表了旋转角度，水平方向的位移就代表缩放因子，由于采样了log对数变换，所以缩放因子可以通过e指数求得，这缩放因子个求解公式就是傅里叶梅林变换公式：
$\delta =e^K$