文章目录
一、正弦序列 ( 数字信号 )
正弦序列 :
x ( n ) = s i n ( ω n ) = s i n ( 2 π f n ) x(n) = sin(\omega n) = sin(2 \pi f n) x(n)=sin(ωn)=sin(2πfn)
ω n \omega n ωn 是要计算正弦的弧度 , n n n 是一个整数值 , ω \omega ω 是角频率 , f f f 是数字频率 ;
ω \omega ω 是角频率的单位是 弧度/秒 , f f f 数字频率单位是 Hz ;
ω = 2 π f \omega = 2 \pi f ω=2πf , 数字频率 乘以 2 π 2\pi 2π 就是角频率 ;
上述 正弦序列 , 是 从模拟信号转换过来的 , 下面介绍原始的模拟信号 ;
二、模拟角频率 与 数字角频率 关系
模拟角频率 与 数字角频率 关系 : ω \omega ω 是 数字角频率 , 注意与 模拟角频率 Ω \Omega Ω 进行区分 , 上述二者之间的关系是 ω = Ω T \omega = \Omega T ω=ΩT ;
T T T 是采样周期 , 也就是多长时间采集一个样本 , 采样频率 F s = 1 T F_s = \cfrac{1}{T} Fs?=T1? ;
如 : 音频采样频率是 F s = 44100 H z F_s = 44100 Hz Fs?=44100Hz , 对应的采样周期 T = 1 44100 T = \cfrac{1}{44100} T=441001? 秒 ;
三、模拟信号
模拟信号 :
x a ( t ) = s i n ( Ω 0 t ) = s i n ( 2 π f 0 t ) x_a(t) = sin(\Omega_0 t) = sin(2 \pi f_0 t) xa?(t)=sin(Ω0?t)=sin(2πf0?t)
上述模拟信号采样频率为 F s F_s Fs? ;
t t t 是时间 , 单位是秒 , Ω 0 \Omega_0 Ω0? 是角频率 , 单位是 弧度/秒 , Ω 0 t \Omega_0 t Ω0?t 是一个弧度值 , 也就是 t t t 秒对应的弧度值 , f 0 f_0 f0? 是模拟频率 , 没有单位 ;
正弦序列 与 模拟信号 之间的关系 : 模拟信号 转 数字信号 ;
x ( n ) = x a ( n T ) = s i n ( Ω 0 n T ) = s i n ( ω n ) x(n) = x_a(nT) = sin(\Omega_0 nT) = sin(\omega n) x(n)=xa?(nT)=sin(Ω0?nT)=sin(ωn)
四、数字角频率 ω 与 模拟角频率 Ω 与 模拟频率 f 的关系
数字角频率 ω \omega ω ( 单位 弧度 ) 与 模拟角频率 Ω 0 \Omega_0 Ω0? 与 模拟频率 f f f 的关系 : ω = Ω 0 T = Ω 0 / F s = 2 π f \omega = \Omega_0 T = \Omega_0 / F_s = 2 \pi f ω=Ω0?T=Ω0?/Fs?=2πf
Ω 0 T \Omega_0 T Ω0?T 分析 : Ω 0 \Omega_0 Ω0? 是 模拟角频率 , 单位是 弧度 / 秒 , T T T 是采样周期 , 单位是 秒 , Ω 0 T \Omega_0 T Ω0?T 计算出来是 弧度 ;
Ω 0 / F s \Omega_0 / F_s Ω0?/Fs? 分析 : F s F_s Fs? 是采样率 , 单位是 Hz , Ω 0 / F s \Omega_0 / F_s Ω0?/Fs? , 弧度/秒 除以 频率 Hz 计算结果是 数字角频率 ;
2 π f 2 \pi f 2πf 分析 : f f f 是数字频率 , 没有单位 , 2 π f 2 \pi f 2πf 是 数字角频率 , 单位是 弧度 ;
五、数字频率 f 与 模拟频率 f0 的关系
数字频率 ( 单位 Hz ) : f = f 0 / F s f = f_0 / F_s f=f0?/Fs?
F s F_s Fs? 是采样率 , 如音频的采样率是 44100 H z 44100Hz 44100Hz ;
模拟频率 f 0 f_0 f0? 除以 采样频率 F s F_s Fs? , 得到的是 数字频率 f f f ;
模拟频率 f 0 f_0 f0? 没有单位 , F s F_s Fs? 采样率单位是 H z Hz Hz , 数字频率 f f f 单位也是 Hz ;
模拟频率 f 0 f_0 f0? 的物理意义 : 频率越高 , 表明其时域波动越剧烈 , 变化越剧烈 ;
六、正弦序列示例
正弦序列 :
x ( n ) = s i n ( ω n ) = s i n ( 2 π f n ) x(n) = sin(\omega n) = sin(2 \pi f n) x(n)=sin(ωn)=sin(2πfn)
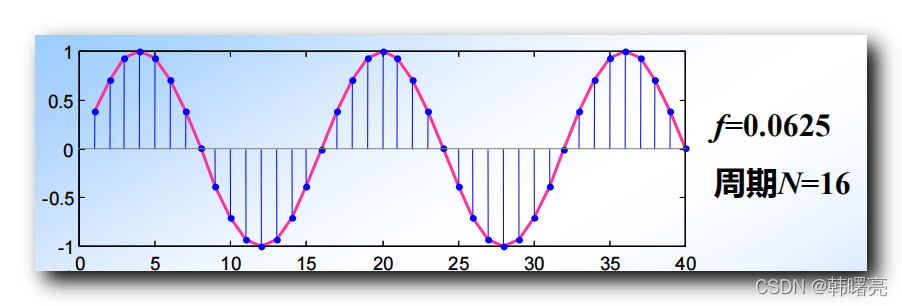
示例一 : 其数字频率 f = 0.0625 f = 0.0625 f=0.0625 , 周期 N = 16 N = 16 N=16 , 也就是每隔 16 16 16 个采样点 , 重复一次 ;
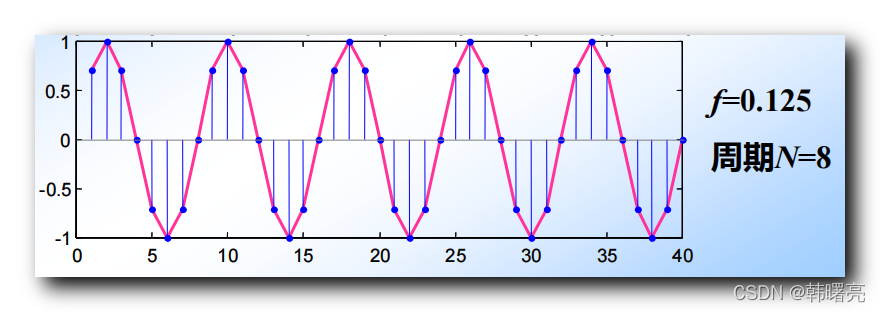
示例二 : 其数字频率 f = 0.125 f = 0.125 f=0.125 , 周期 N = 8 N = 8 N=8 , 也就是每隔 8 8 8 个采样点 , 重复一次 ;