[数据结构与算法]浅议kmp算法

需求提出
给定一个模式串 pattern = “ddywabcdababcdabd” 和一个子串 substr = “abcdabd”，需判断 pattern 中是否包含 substr，如果包含，返回 substr 第一次在 pattern 中出现的位置；如果不包含，返回 -1（常用手段）

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;
/*
* Author: 酒馆店小二
* Description: kmp算法学习
* Date: 2022-2-17 22:41:52 星期四
* FileName: kmp.cpp
* Location: D:\VSCODE_CPP\algorithm\kmp\kmp.cpp
*/

vector<int> kmpNext(string substr) {  //KMP next 数组
    int n = substr.size();
    vector<int> next(n);
    for (int i = 1, j = 0; i < n; ++i) {
        while (j > 0 && substr[i] != substr[j]) {
            j = next[j - 1];
        }
        if (substr[i] == substr[j]) {
            j++;
        }
        next[i] = j;
    }
    return next;
}

int kmpMatch(string pattern, string substr) {  // KMP匹配法
    int pLen = pattern.size();
    int sLen = substr.size();
    vector<int> next = kmpNext(substr);
    for (int i = 0, j = 0; i < pLen; i++) {
        while (j > 0 && pattern[i] != substr[j]) {
            j = next[j - 1];
        }
        if (pattern[i] == substr[j]) {
            j++;
        }
        if (j == sLen) {
            return i - j + 1;
        }
    }
    return -1;
}

int main(int argc, char *argv[]){
    string pattern = "ddywabcdababcdabd";
    string substr = "abcdabd";
    cout << "Match position is: " << kmpMatch(pattern, substr) << endl;

    return 0;
}

赶时间的小伙伴可以拿去应急了。

第一章 暴力匹配实现

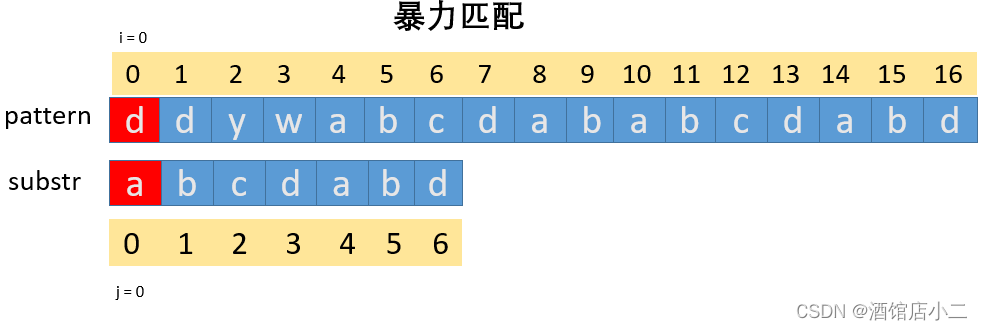
第一次匹配不符合后，子串向后移一位，从头再开始匹配

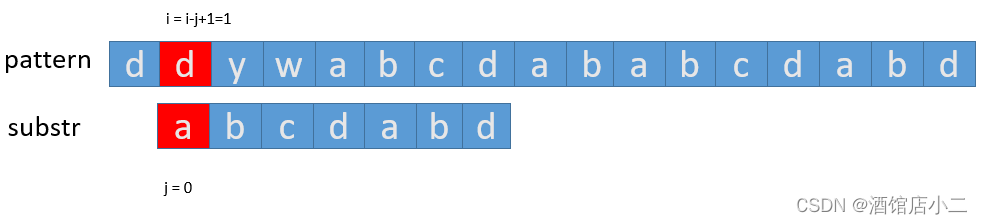
省略若干次移动。。。
就这样一位位的匹配、一位位的移动，最后当 j == substr.size() 时，匹配结束
ps: 当最后一位 d 匹配时，j 会再加一位，代码中的 ++j，所以 j == substr.szie()

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;
/*
* Author: 酒馆店小二
* Description: kmp算法学习
* Date: 2022-2-17 22:41:52 星期四
* FileName: kmp.cpp
* Location: D:\VSCODE_CPP\algorithm\kmp\kmp.cpp
*/

int violentMatch(const string &pattern, const string &substr) {
    int pLen = pattern.size();
    int sLen = substr.size();
    int i = 0, j = 0; // i、j 分别指向 pattern 和 substr 的下标
    while (i < pLen && j < sLen) {
        if (pattern[i] == substr[j]) { // 当前字符匹配成功
            i++;
            j++;
        } else { // 当前字符匹配失败
            i = i - j + 1;
            j = 0;
        }
    }
    if (j == sLen) { // 匹配成功，返回子串在模式串中的位置，否则返回 -1
        return i - j;
    } else {
        return -1;
    }
}

int main(int argc, char *argv[]){
    string pattern = "ddywabcdababcdabd";
    string substr = "abcdabd";
    cout << "Match position is: " << violentMatch(pattern, substr) << endl;

    return 0;
}

上面的程序是没有问题的，但不够好！（正如高中时候数学老师的一句话：我不能说你错，只能说你不对~~~）
上述程序的时间复杂度是O(mn)，m、n是两个字符串的长度。聪明的程序员们是无法接受这样的时间开销的，于是就有了KMP算法的产生。

第二章 KMP历史渊源

Knuth-Morris-Pratt 算法，由 Donald Knuth、James H. Morris 和 Vaughan Pratt 三人于 1977 年联合发表，因此人们称他为克努特—莫里斯—普拉特操作（简称KMP算法）（所谓名垂青史就是这么个情况）。KMP主要应用在字符串匹配的场景中，其主要思想是当出现字符串不匹配的情况时，记录之前部分已经匹配的文本内容，利用 next 数组避免从头匹配，从而提高匹配效率，next 数组是KMP算法的核心和难点。KMP算法的时间复杂度O(m+n)，而使用暴力匹配的时间复杂度则是O(mn)，匹配规模越大，KMP算法的优势越明显。

第三章 KMP算法原理

1、首先，用 pattern 的第一个字符和 substr 的第一个字符去比较，不符合，substr 向后移动一位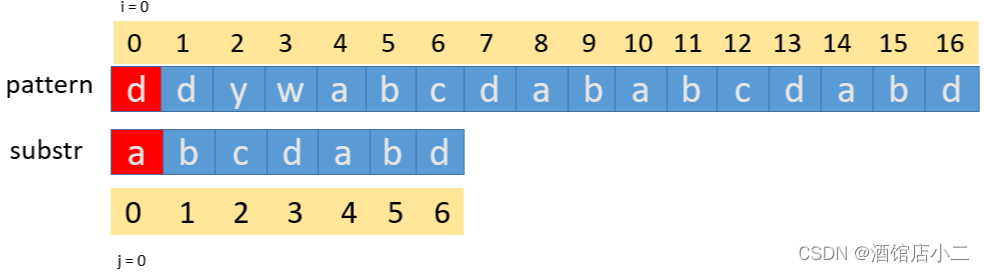
2、比较二者字符，不符合，后移。

3、比较二者字符，不符合，后移。

4、直到遇到匹配的元素，于是双方的下标向后移动，遇到 pattern 有一个字符与 substr 对应的字符不符合。
5、此时按照暴力的思想是将子串向后移一位，再从头比较（亏损做法）
6、其实这样很不划算，因为此时”abcdab”已经比较过了，我们知道了
pattern[5] = substr[1] = b，但是后移一位的效果是 pattern[5] 跟 substr[0] 比较，而
substr[0] != substr[1]，所以肯定匹配失败。KMP算法的想法是，设法利用这个已知信息，不要把”搜索位置“移回已经比较过的位置，而是继续把他（子串下标）向后移，这样就提高了效率。怎么做到把刚刚重复的步骤省略掉？可以对 substr 计算出一张《匹配表》，这张表的产生在后面介绍。

7、此时需要看子串已匹配字符的前一个字符对应的下标，此处是模式串的 a 和子串的 d 不匹配，于是需要看子串前一个字符在匹配表中对应的下标，也就是 b 的下标，根据查表可以得知，b 下标应该是2。这是什么意思呢？— 就是说，模式串不动，子串移动到下标为2的位置来与模式串匹配，暴力匹配是模式串的 a 与子串的 d 比较，KMP算法是模式串的 a 与子串的 c 比较，可以发现，模式串并没有回溯较多位置，子串也没有从头比较。

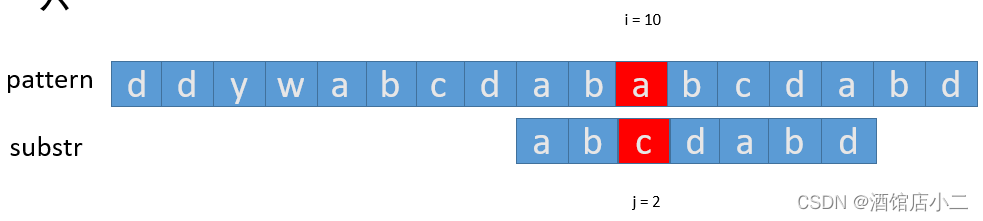
8、模式串的 a 与子串的 c 不匹配，于是我们查看此时子串的前一个字符在匹配表中对应的下标，即 b 对应的下标，为 0，意思就是模式串不动，将子串的下标移到 0 处，挨着挨着比较，最终匹配成功。返回结果是10（因为从模式串的下标10的位置处第一次出现了完整的子串）。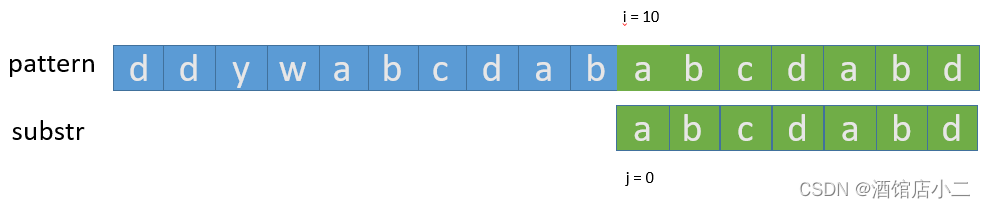
KMP 算法如此高效，匹配表功不可没，俗称：next 数组。next数组的介绍如下。

第四章 KMP的匹配表（next数组）

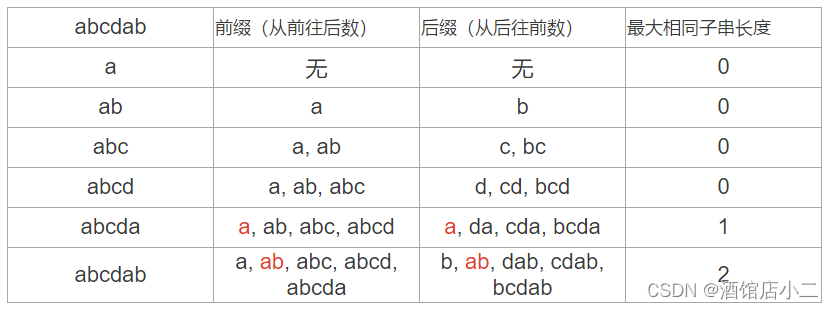
介绍匹配表如何产生之前，我们首先介绍什么是前缀什么是后缀？

• 什么是前缀：包含首字母但不包含尾字母的所有子串。
• 什么是后缀：包含尾字母但不包含首字母的所有子串。

这里以模式串“abcdab”为例，该模式串的前缀和后缀依次如下表：

于是匹配表就做好了，使用方法见前面。

第五章 KMP算法代码实现

代码随想录的作者 carl 大佬在b站有视频：
理论篇：https://www.bilibili.com/video/BV1PD4y1o7nd
代码篇：https://www.bilibili.com/video/BV1M5411j7Xx

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>

using namespace std;
/*
* Author: 酒馆店小二
* Description: kmp算法学习
* Date: 2022-2-17 22:41:52 星期四
* FileName: kmp.cpp
* Location: D:\VSCODE_CPP\algorithm\kmp\kmp.cpp
*/

vector<int> kmpNext(string substr) {  //KMP next 数组
    int n = substr.size();
    vector<int> next(n);
    for (int i = 1, j = 0; i < n; ++i) {
        while (j > 0 && substr[i] != substr[j]) {
            j = next[j - 1];
        }
        if (substr[i] == substr[j]) {
            j++;
        }
        next[i] = j;
    }
    return next;
}

int kmpMatch(string pattern, string substr) {  // KMP匹配法
    int pLen = pattern.size();
    int sLen = substr.size();
    vector<int> next = kmpNext(substr);
    for (int i = 0, j = 0; i < pLen; i++) {
        while (j > 0 && pattern[i] != substr[j]) {
            j = next[j - 1];
        }
        if (pattern[i] == substr[j]) {
            j++;
        }
        if (j == sLen) {
            return i - j + 1;
        }
    }
    return -1;
}

int main(int argc, char *argv[]){
    string pattern = "ddywabcdababcdabd";
    string substr = "abcdabd";
    cout << "Match position is: " << kmpMatch(pattern, substr) << endl;

    return 0;
}

笔者水平有限，有不妥的地方，请多指教。

最是人间留不住，朱颜辞镜花辞树。
2022.2.17