[数据结构与算法]Day34=====

开始学习中等题了！！

688、骑士在棋盘上的概率

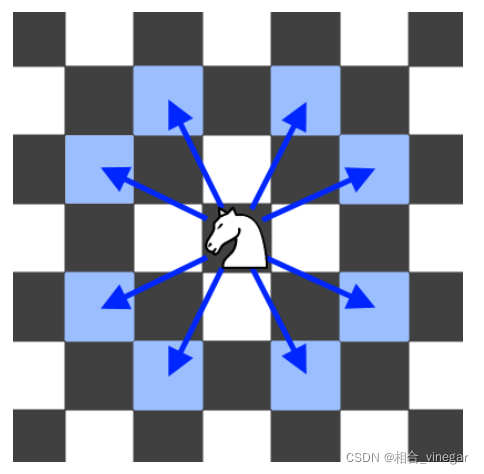
在一个 n x n 的国际象棋棋盘上，一个骑士从单元格 (row, column) 开始，并尝试进行 k 次移动。行和列是 从 0 开始 的，所以左上单元格是 (0,0) ，右下单元格是 (n - 1, n - 1) 。象棋骑士有8种可能的走法，如下图所示。每次移动在基本方向上是两个单元格，然后在正交方向上是一个单元格。每次骑士要移动时，它都会随机从8种可能的移动中选择一种(即使棋子会离开棋盘)，然后移动到那里。————故概率的分母是8^k（8的k次方）骑士继续移动，直到它走了 k 步或离开了棋盘，返回骑士在棋盘停止移动后仍留在棋盘上的概率。

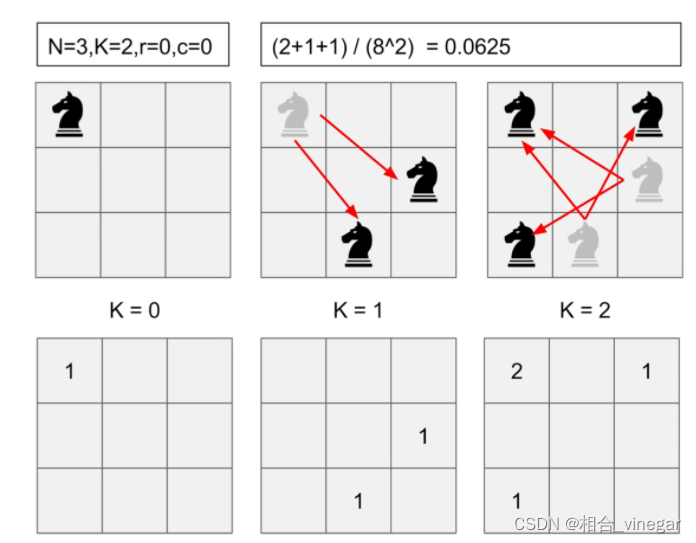
k=2是在k=1的位置上再走的，即k=1时位置是两个黑马的其中一个，

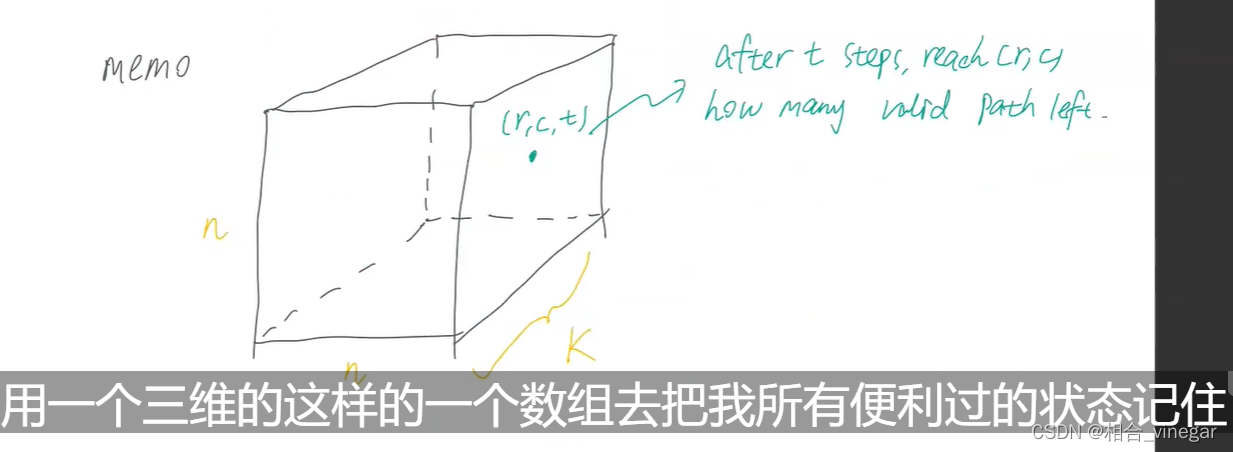
?用一个三维的数组去把我所便利过的状态记住，这样的话下次再遍历到这个状态的时候就可以直接取值，而不是重新算一遍

class Solution {
    //动态规划
    private static int[][] DIRS = {{1, 2}, {2, 1}, {-1, 2}, {-2, 1}, {1, -2}, {2, -1}, {-1, -2}, {-2, -1}};

    public double knightProbability(int n, int k, int row, int column) {
        //dp定义：dp[l][i][j]:走l步移动的时候，到达（i，j）的概率
        //每步的移动在基本方向上是两个单元格，然后在正交方向上是一个单元格。
        double[][][] dp = new double[k + 1][n][n];//定义dp 

//dp[s][i][j]=(dp[s-1][i+2][j+1]+dp[s-1][i+1][j+2]+....)/8 八种方向不同的概率相加再除以8
        for (int l = 0; l <= k; l++) {//遍历步数
            for (int i = 0; i < n; i++) {//遍历行
                for (int j = 0; j < n; j++) {//遍历列
                    if (l == 0) {
                        dp[l][i][j] = 1;//初始化
                    } else {
                        for (int[] dir : DIRS) {
                            int x = i + dir[0];//横坐标
                            int y = j + dir[1];//纵坐标
                            if (x >= 0 && x < n && y >= 0 && y < n) {
                                dp[l][i][j] += dp[l - 1][x][y] / 8; //算出概率的公式
                            }
                        }
                    }
                }
            }
        }

        return dp[k][row][column];
    }
}