[数据结构与算法]【并查集】union和find的几种实现

以上指的是单次操作的时间复杂度是，且union里调用find所用的时间不算。

quick-find

保证当且仅当id[p]等于id[q]时p和q是连通的，即同一连通分量中所有触点在数组中的值全部相同。
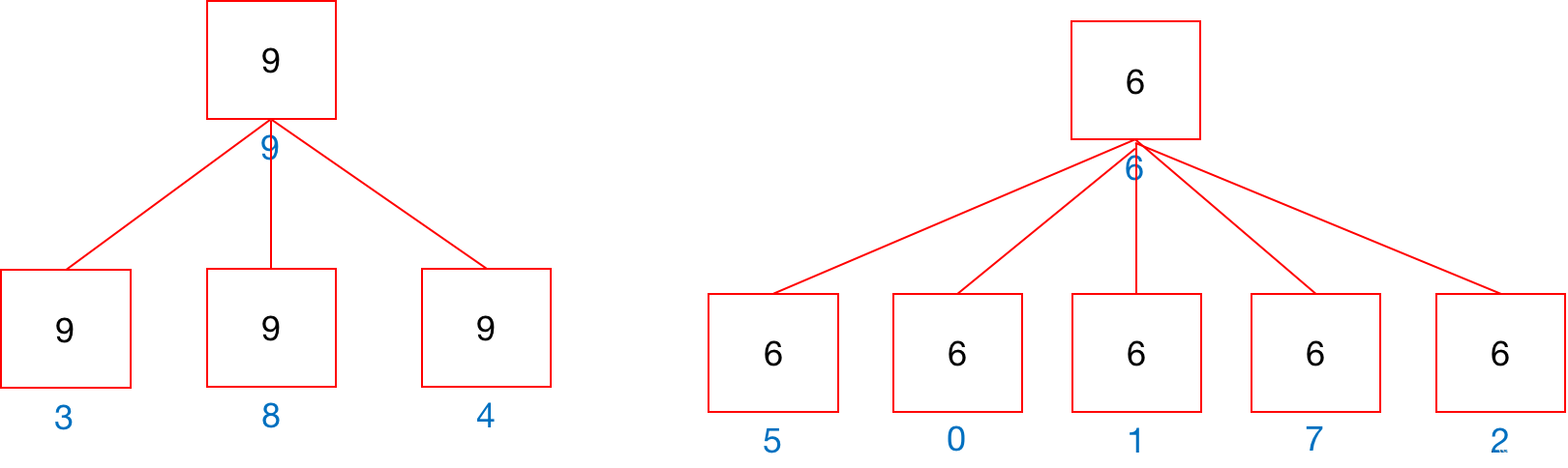
比如有以下两个连通分量，标识符分别为9和6。
触点3、8、4和9属于分量9；
触点5、0、1、7、2和6属于分量6。

实现

union_find.h

#ifndef UNION_FIND
#define UNION_FIND

#include <vector>

class UF {
public:
    UF(size_t N);
    ~UF();

    size_t Count() const;
    void Union1(size_t p, size_t q);
    size_t Find1(size_t p) const;

private:
    std::vector<size_t> id;
    size_t count_;
};

#endif

union_find.cpp

#include "union_find.h"

UF::UF(size_t N) : id(N)
{
    for (size_t i = 0; i < N; ++i) {
        id[i] = i;
    }
    count_ = N;
}

UF::~UF() {}

void UF::Union1(size_t p, size_t q)  // 连接p所在分量和q所在分量
{
    int fp = Find1(p);
    int fq = Find1(q);

    if (fp == fq) {
        return;
    }

    for (int i = 0; i < id.size(); ++i) {
        if (id[i] == fq) {
            id[i] = fp;  // 把q所在的分量上的所有触点连接到p所在的分量上
        }
    }

    --count_;
}

size_t UF::Find1(size_t p) const   // 返回p的分量标识符
{
    return id[p];
}

size_t UF::Count() const
{
    return count_;
}

分析

这种实现的find()操作的速度是很快的，只需访问一次数组，即O(1)的时间复杂度。但每次的union()操作都需要遍历一次数组，即O(n)的时间复杂度。因此无法处理存在大量触点的问题。

quick-union

每个触点所对应的id数组元素值都是同一个分量中的另一个触点的名称，我们将这种关系称为连接。从某个触点开始，可以找到它连接的另一个触点，再找到下一个连接的触点，直到根触点（连接指向自己）。
当且仅当分别由两个触点开始到达同一个根触点时，它们存在于同一个连通分量之中。
连通分量被表示为“树”型结构，可如下表示：9和6分别是它们所在分量的根触点。

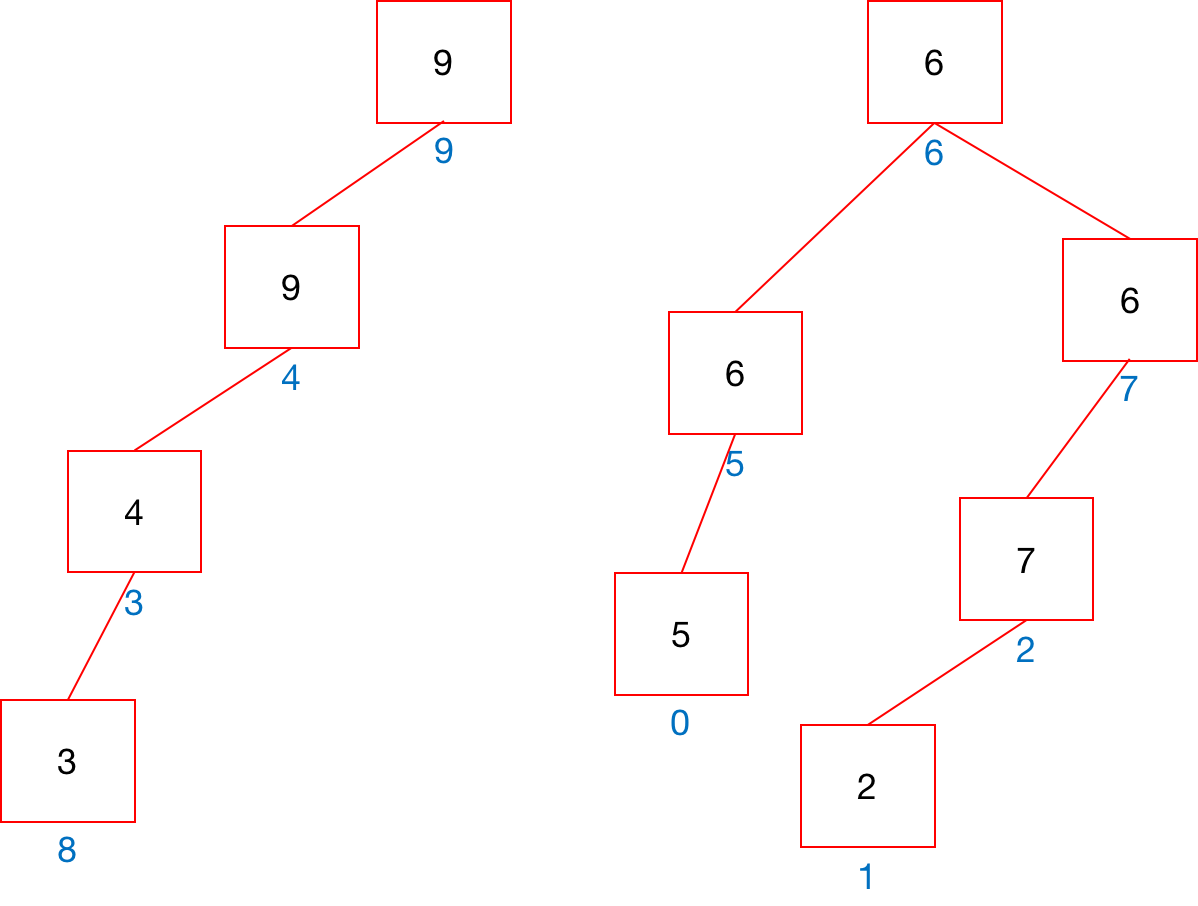
可以发现，quick-find是quick-union的扁平化版本，前者树的深度<=1，后者树的深度<=N

实现

void UF::Union2(size_t p, size_t q)
{
    int fp = Find2(p);
    int fq = Find2(q);
    if (fp == fq) {
        return;
    }

    id[fq] = fp; // 把q所在分量的根触点加在p所在分量的根触点上
    --count_;
}

size_t UF::Find2(size_t p) const
{
    while (p != id[p]) {
        p = id[p];
    }
    return p;
}

分析

find()：沿着起始触点一步步地找它对应的连接触点，直至找到根触点并返回它。最差情况下（树会变得很深，每新增一个触点，树的深度都加1），find的时间复杂度为O(n)。
union()：把一个分量的根触点连接到另一个分量的根触点上，完成两个分量的合并。时间复杂度为O(1)。综合性能比quick-find好一些了。
如union(9, 6);

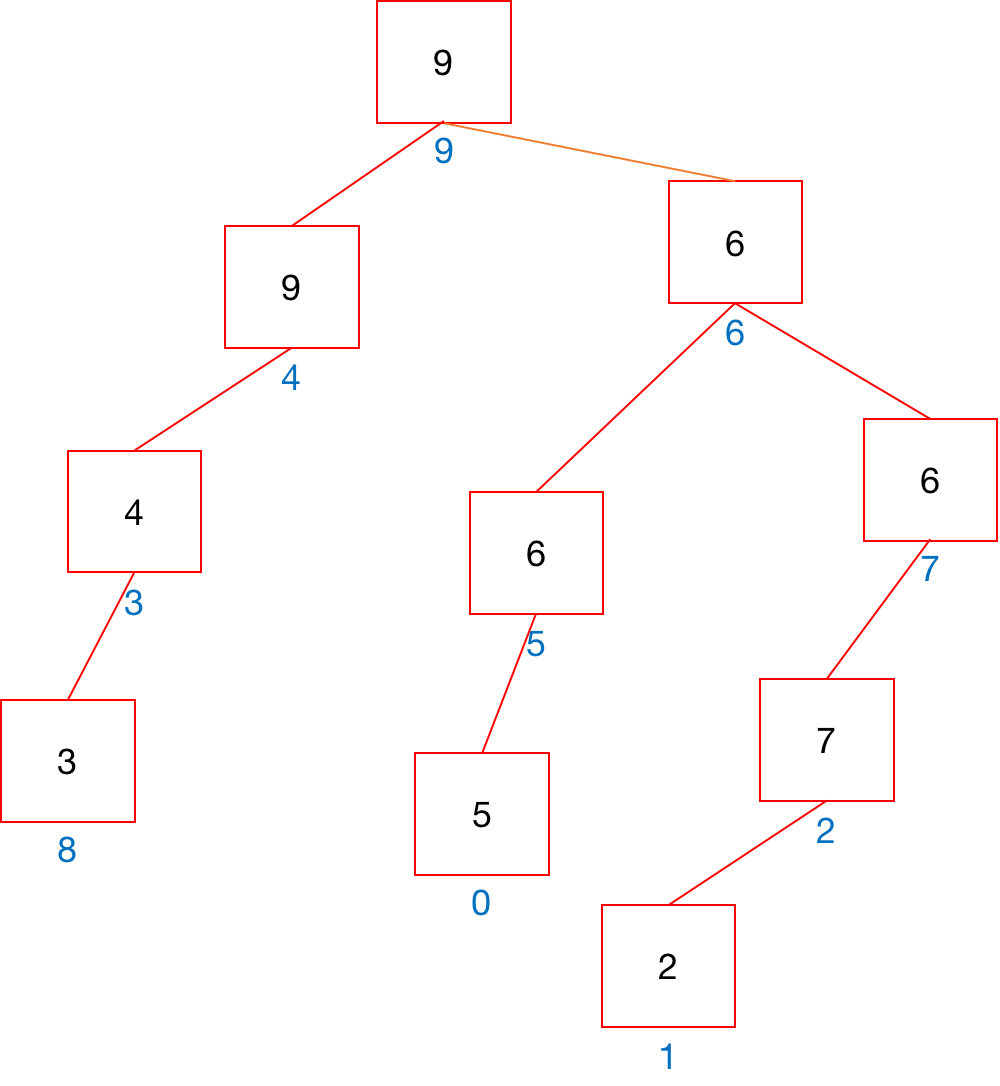
加权quick-union

find()：和quick-union一样；
union()：合并两个分量时，多一个判断，把小树加在大树上，防止树变得过深。

实现

sz[i]表示以触点i为根的“树”所包含的触点个数，即树的大小。

void UF::Union3(size_t p, size_t q)
{
    int fp = Find2(p);
    int fq = Find2(q);
    if (fp == fq) {
        return;
    }

    if (sz[fp] < sz[fq]) {
        id[fp] = fq;
        sz[fq] += sz[fp];
    } else {
        id[fq] = fp;
        sz[fp] += sz[fq];
    }
    --count_;
}

分析

虽然多了一次判断，但union的时间复杂度依然是O(1)。
通过防止树变得过深，优化了find，避免了最差情况的发生。

路径压缩的加权quick-union

路径压缩是指尽量让树的结构看起来像quick-find那样扁平，在不损失union()性能的前提下进一步优化find()的时间复杂度。

实现

union操作和加权quick-union的一样。
find操作要遍历两次从当前触点到根触点的路径。第一次找到根触点，第二次使沿途的触点直接指向根触点。

size_t UF::Find4(size_t p) const
{
    int fp = id[p];
    while (fp != id[fp]) { // 找到根触点
        fp = id[fp];
    }

    while (p != fp) {
        int nxt = id[p];
        id[p] = fp; // 将触点直接连接到根触点
        p = nxt;
    }

    return fp;
}

分析

通过在遍历触点的同时将它们直接连接到根触点，进一步降低了树的深度，在保证union性能不变的情况下，优化了find。