所谓区间问题,就是线段问题,让你合并所有线段、找出线段的交集等等。主要有两个技巧:
排序:常见的问题排序方法基本是按照区间起点排序,若起点相同,则按照中点排序,如果对一道区间类的题无从下手的话,可以先对区间排序再去寻找规律。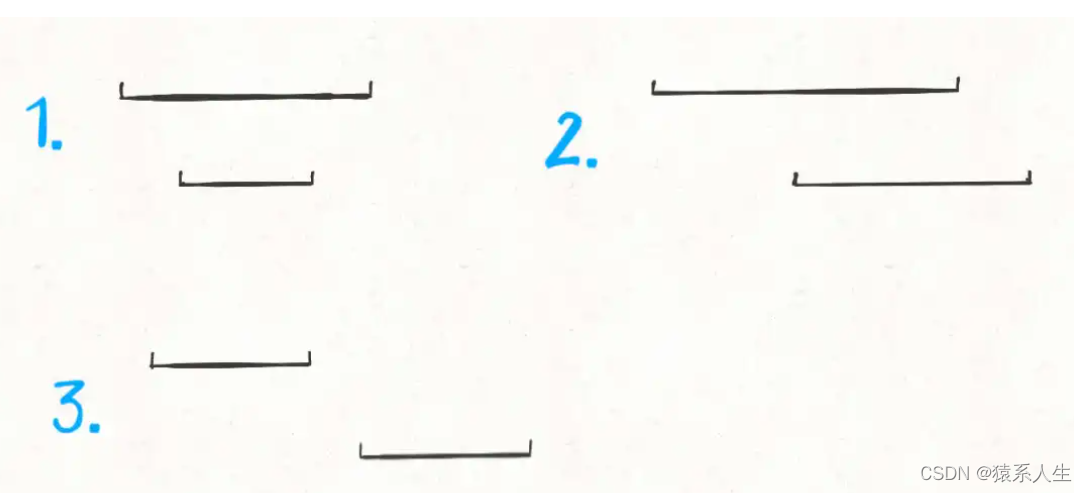
排完序之后会出现上述三种情况
1.上面的区间覆盖下面的区间;
2.上下两个区间相交
3.两个区间不相交。
明白了上述三种情况大多数区间问题都可以解决。
1.删除被覆盖区间
leetcode1288题
要求:给你一个区间列表,请你删除列表中被其他区间所覆盖的区间。只有当?c <= a?且?b <= d?时,我们才认为区间?[a,b) 被区间?[c,d) 覆盖。在完成所有删除操作后,请你返回列表中剩余区间的数目。
基本思路:满足上图中的第一种情况就是本题的解,当满足覆盖,覆盖区间+1,不满足覆盖条件时,顶层区间就变成了当前区间的左右边界。
具体代码如下
```Java
public static int removeCoveredIntervals(int[][] intervals) {
? ? ? ? //区间按照起点升序,终点降序排序
? ? ? ? Arrays.sort(intervals, new Comparator<int[]>() {
? ? ? ? ? ? @Override
? ? ? ? ? ? public int compare(int[] o1, int[] o2) {
? ? ? ? ? ? ? ? return o1[0]==o2[0]?o2[1]-o1[1]:o1[0]-o2[0];
? ? ? ? ? ? }
? ? ? ? });
? ? ? ? int left=intervals[0][0];int right=intervals[0][1];//定义顶层区间左右边界
? ? ? ? int res=0;//覆盖区间数量
? ? ? ? for(int i=1;i<intervals.length;i++){
? ? ? ? ? ? int[] intv=intervals[i];
? ? ? ? ? ? //覆盖条件,第一个条件恒成立的,可以删掉
? ? ? ? ? ? if(intv[0]>=left&&intv[1]<=right){
? ? ? ? ? ? ? ? res+=1;
? ? ? ? ? ? }else{
? ? ? ? ? ? left=intv[0];right=intv[1];
? ? ? ? }
? ? }
? ? ? ? return intervals.length-res;
? ? }
```2.区间合并问题
leetcode56题
要求:给出一个区间的集合,请合并所有重叠的区间。
基本思路:满足上图中1和2两种情况就会发生区间合并,合并之后的区间取顶层区间的左边界,右边界取两者之间的最大值。
具体代码如下:
```Java
public static int[][] merge(int[][] intervals) {
? ? ? ? //排序
? ? ? ? Arrays.sort(intervals, new Comparator<int[]>() {
? ? ? ? ? ? @Override
? ? ? ? ? ? public int compare(int[] o1, int[] o2) {
? ? ? ? ? ? ? ? return o1[0]==o2[0]?o2[1]-o1[1]:o1[0]-o2[0];
? ? ? ? ? ? }
? ? ? ? });
? ? ? ? int left=intervals[0][0];int right=intervals[0][1];
? ? ? ? int[][] res=new int[1][2];
? ? ? ? res[0]=intervals[0];
? ? ? ? for(int i=1;i<intervals.length;i++){
? ? ? ? ? ? int[] intv=intervals[i];
? ? ? ? ? ? //1.覆盖会发生合并,不发生任何操作,当前区间还是顶层区间
? ? ? ? ? ? //2.相交会发生合并,顶层区间发生改变
? ? ? ? ? ? if(intv[0]<=right&&intv[1]>=right){
? ? ? ? ? ? ? ? right=intv[1];
? ? ? ? ? ? ? ? res[res.length-1][1]=right;
? ? ? ? ? ? }
? ? ? ? ? ? //3.不相交,直接输出当前数组
? ? ? ? ? ? else if(intv[0]>=right){
? ? ? ? ? ? ? ? left=intv[0];right=intv[1];
? ? ? ? ? ? ? ? res=arrAdd(res, new int[]{left, right});
? ? ? ? ? ? }
? ? ? ? }
? ? ? ? return res;
? ? }
? ? public static int[][] arrAdd(int[][] arr,int[] target){
? ? ? ? arr=Arrays.copyOf(arr,arr.length+1);
? ? ? ? arr[arr.length-1]=target;
? ? ? ? return arr;
? ? }
```