一、二叉查找（排序）树

1.概念

（1）.定义

二叉查找树就是一颗二叉树，他的左节点比父节点要小，右节点比父节点要大，它的高度决定查找效率

（2）.特点

二叉排序树中，如果其根结点有左子树，那么左子树上所有结点的值都小于根结点的值；
二叉排序树中，如果其根结点有右子树，那么右子树上所有结点的值都大小根结点的值；
二叉排序树的左右子树也要求都是二叉排序树；

2.BST操作

（1）.查找

从根节点开始查找

查找值比当前值大，则搜索右子树
查找值比当前值小，则搜索左子树
查找值等于当前值，停止查找，返回当前节点

（2）.插入

要插入节点，则必须先找到插入节点的位置。 ???

从根节点开始查找：

要插入的值比当前节点的值大，则比较右子树 ???????
要插入的值比当前节点的值小，则比较左子树 ???????
要插入的值和当前节点的值相等，因为二叉查找树不存在两个相同值的节点，所以不执行插入操作。 ???

直到比较到左右子树为空时，则插入到对应位置。

（3）.遍历

前（根）序遍历：根左右 ???????
中（根）序遍历：左根右 ???????
后（根）序遍历：左右根

（4）.查找最小值节点

从根节点开始，不断查询当前节点的左子节点，直到最后一个不为空的节点，该节点就是整棵树的最小值节点。

（5）.查找最大值节点

从根节点开始，不断查询当前节点的右子节点，直到最后一个不为空的节点，该节点就是整棵树的最大值节点。

（6）.查找前驱节点

前驱节点：小于当前节点的最大值节点 ???

即： ???????

当前节点有左子树时，其前驱节点就是其左子树中的最大值节点???
当前节点没有左子树，则向上递归到第一次左拐时节点的父节点就是其前驱节点

（7）.查找后继节点

后继节点：大于当前节点的最小值节点 ???

即： ???????

当前节点有右子树时，其后继节点就是其右子树中的最小值节点
当前节点没有右子树时，则向上递归到第一次右拐时节点的父节点就是其后继节点

（8）.删除

删除操作前提：删除要保证删除后，BST树的节点还能保证有序 ???

删除操作本质：是用被删除节点的前驱节点或者后继节点来替代。 ???????

叶子节点直接删除（叶子节点即没有前驱和后继节点的节点） ???????
只有一个子节点的节点被删除，就用它的唯一的子节点来代替。（单子节点即只有前驱节点，或者只有后继节点的节点） ???????
有两个子节点的，需要找到替代节点（双子节点，既有前驱节点，也有后继节点的节点）

二、二叉平衡树

1.概念

（1）.定义

BST有一种极端情况，就是全左倾树，或者全右倾树。

（2）.特点

AVL树是一个高度自平衡的树，即AVL树的根节点的左右子树的高度差不超过绝对值1。且左右子树本身也是二叉平衡树。另外AVL树具备BST树的全部特性。 ???

AVL树查询的时间复杂度为O（logN）,即每次查询都是二分查找。

2.AVL树的旋转操作

当AVL树中插入新节点时，就可能出现左右子树高度差超过1的情况，此时AVL树就会进行旋转操作，来改变树的结构以保证平衡性，即将左右子树高度差降为1.

（1）.左旋

以某个节点作为旋转点，其右子节点变为旋转节点的父节点，右子节点的左子节点变为旋转节点的右子节点，左子节点保持不变。

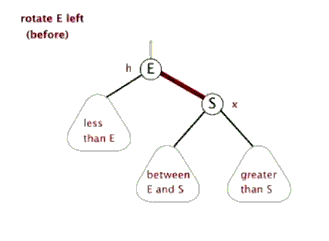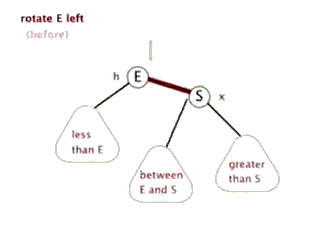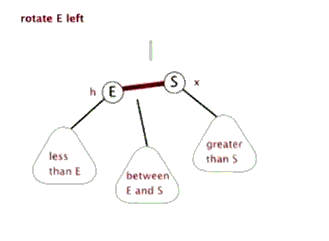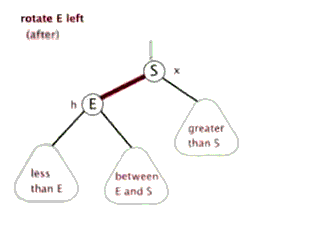
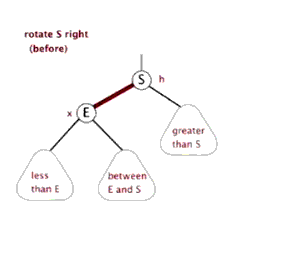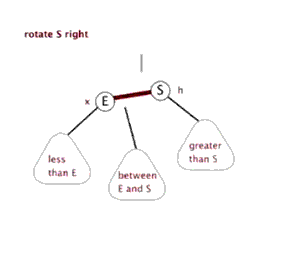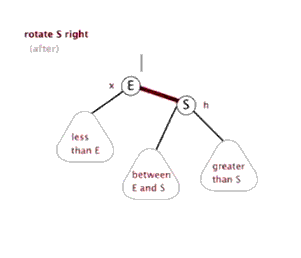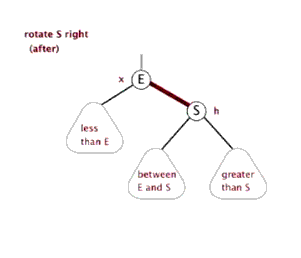
（2）.右旋

以某个节点作为旋转点，其左子节点变为旋转节点的父节点，左子节点的右子节点变为旋转节点的左子节点，右子节点保持不变。

三、2-3-4树

1.概念

234树是四阶的平衡树（Balance Tree）,它属于多路查找树

所有叶子节点都拥有相同的深度
节点只能是2-节点，3-节点，4-节点之一
2-节点：包含一个元素的节点，有两个子节点
3-节点：包含两个元素的节点，有三个子节点
4-节点：包含三个元素的节点，有四个子节点
所有节点至少包含一个元素
元素始终保持排序顺序，整体上保持二叉查找树的特性，节点的元素大于它的左子树所有节点的元素，小于它的右子树所有节点的元素。当节点有多个元素时，每个元素必须大于它左边和它左子树中的元素。