智能优化算法:人工大猩猩部队优化算法
摘要:人工大猩猩部队优化算法(Artificial gorilla troops optimizer,GTO),是于2021年提出的一种新型智能优化算法,该算法主要通过,模拟大猩猩全体的生活行为来进行寻优,具有寻优能力强,收敛速度快等特点。
1.算法原理
GTO通常遵循以下几个规则来搜索解决方案:
1.GTO算法的优化空间包含三种类型的解决方案,其中X被称为大猩猩的位置向量,GX被称为大猩猩候选位置向量,在每个阶段创建,如果其性能优于当前解决方案,则更新。最后,银背猩猩silverback是每次迭代中找到的最佳解决方案。
2.考虑到为优化操作选择的搜索种群的数量,整个群体中只有一只银背猩猩。
3.三种类型的X、GX和silverback解决方案精确模拟了大猩猩在自然界中的社交生活。
4.大猩猩可以通过寻找更好的食物来源或在一个公平而强壮的群体中定位来增加它们的力量。在GTO中,在GTO算法中称为GX的每次迭代中都会创建解决方案。如果找到的解决方案是新的(GX),它将替换当前的解决方案(X)。否则,它将保留在内存中(GX)。
5.大猩猩倾向于集体生活,因此无法单独生活。因此,他们作为一个群体寻找食物,并继续生活在一个银背猩猩的领导下,领导着所有的群体决策。在我们的公式化阶段,假设种群中最差的解是大猩猩群中最弱的成员,大猩猩试图避开最差的解,接近最佳解(银背),从而改善大猩猩的所有位置。
1.1勘探阶段
该阶段主要是对空间进行全局搜索,的数学模型如下:
G
X
(
t
+
1
)
=
{
(
U
B
?
L
B
)
×
r
1
+
L
B
,
?rand?
<
p
(
r
2
?
C
)
×
X
r
(
t
)
+
L
×
H
,
?rand?
≥
0.5
X
(
i
)
?
L
×
(
L
×
(
X
(
t
)
?
G
X
r
(
t
)
)
)
+
r
3
×
(
X
(
t
)
?
G
X
r
(
t
)
)
,
?rand?
<
0.5
(1)
G X(t+1)= \begin{cases}(U B-L B) \times r_{1}+L B, & \text { rand }<p \\ \left(r_{2}-C\right) \times X_{r}(t)+L \times H, & \text { rand } \geq 0.5 \\ X(i)-L \times\left(L \times\left(X(t)-G X_{r}(t)\right)\right)+r_{3} \times\left(X(t)-G X_{r}(t)\right), & \text { rand }<0.5\end{cases}\tag{1}
GX(t+1)=??????(UB?LB)×r1?+LB,(r2??C)×Xr?(t)+L×H,X(i)?L×(L×(X(t)?GXr?(t)))+r3?×(X(t)?GXr?(t)),??rand?<p?rand?≥0.5?rand?<0.5?(1)
其中,
p
p
p 是一个给定的介于 0 到 1 之间的参数,该参数确定选择迁移机制到末知位置的概率;
G
X
(
t
+
1
)
G X(t+1)
GX(t+1) 是下次迭代时大猩猩个体的候选位置向量;
X
(
t
)
X(t)
X(t) 是大猩猩个体的当前位置向;
r
1
,
r
2
,
r
3
r_{1}, r_{2}, r_{3}
r1?,r2?,r3? 和
r
a
n
d
r a n d
rand 是在每次迭代中更新 的范围为 0 到 1 的随机值;
U
B
U B
UB 和
L
B
L B
LB 分别表示变量的 上限和下限;
X
r
X_{r}
Xr? 和
G
X
r
G X_{r}
GXr? 分别是从整个种群中随机选择的大猩猩中的一员,随机选择的大猩猩候选位置向量,包括每个阶段更新的位置;
C
,
L
C,L
C,L 和
H
H
H 的计算如下:
C
=
F
×
(
1
?
I
t
M
a
x
I
t
)
(2)
C=F \times\left(1-\frac{I t}{M a x I t}\right)\tag{2}
C=F×(1?MaxItIt?)(2)
F = cos ? ( 2 × r 4 ) + 1 (3) F=\cos \left(2 \times r_{4}\right)+1 \tag{3} F=cos(2×r4?)+1(3)
L = C × l (4) L=C \times l \tag{4} L=C×l(4)
H = Z × X ( t ) (5) H=Z \times X(t)\tag{5} H=Z×X(t)(5)
Z = [ ? C , C ] (6) Z=[-C, C]\tag{6} Z=[?C,C](6)
其中, I t I t It 是当前迭代次数, M a x I t MaxIt MaxIt为最大迭代次数, cos ? \cos cos 表示余弦函数, r 4 r_{4} r4? 是0到1的随机值; l l l 为-1到1之间随机值。, Z Z Z是问题维度中范围为 [ ? C , C ] [-C, C] [?C,C] 的随机值。在探索阶段结束时,计算所有 G X G X GX 个体的适应度值,如果适应度值满足 G X ( t ) < X ( t ) G X(t)<X(t) GX(t)<X(t) ,则使用 G X ( t ) G X(t) GX(t) 个体作为 X ( t ) X(t) X(t) 新个体。并且该阶段产生的最优个体被视为银背大猩猩即最优解。
1.2 开发阶段
在GTO算法的开发阶段,采用了跟随银背大猩猩和竞争成年雌性的两种行为。银背大猩猩领导一个群体,做出所有决定,决定群体的行 动,并引导大猩猩走向食物来源。它还负责团队的安全和福祉,团队中的所有大猩猩都遵守银背大猩猩的所有决策。另一方面,银背大猩 猩可能会变弱、变老并最终死亡,群体中的黑背大猩猩可能会成为群体的领导者,或者其他雄性大猩猩可能会与银背大猩猩交战并主宰群 体。开发阶段使用的两种机制所述,可以使用式(2)中的数值选择跟随银背或竞争成年此惟。如果 C ≥ W C \geq W C≥W ,则选择跟随银背机制,但如 果 C < W C<W C<W ,则选择竞争成年雌性机制。 W W W 是优化操作之前要设置的参数。
1.2.1 跟随银背大猩猩
如果
C
≥
W
C \geq W
C≥W ,则选择跟随银背大猩猩机制,其行为如式(7)所示:
G
X
(
t
+
1
)
=
L
×
M
×
(
X
(
t
)
?
X
silverback?
)
+
X
(
t
)
(7)
G X(t+1)=L \times M \times\left(X(t)-X_{\text {silverback }}\right)+X(t)\tag{7}
GX(t+1)=L×M×(X(t)?Xsilverback??)+X(t)(7)
M = ( ∣ 1 N ∑ i = 1 N G X i ( t ) ∣ g ) 1 g (8) M=\left(\left|\frac{1}{N} \sum_{i=1}^{N} G X_{i}(t)\right|^{g}\right)^{\frac{1}{g}}\tag{8} M=(∣∣∣∣∣?N1?i=1∑N?GXi?(t)∣∣∣∣∣?g)g1?(8)
g = 2 L (9) g=2^{L}\tag{9} g=2L(9)
其中, X ( t ) X(t) X(t) 是大猩猩的位置向量, X silverback? X_{\text {silverback }} Xsilverback?? 是银背大猩猩的位置向量(最佳位置),此外, L L L 由式(4)计算, M M M 由式(8)计算; G X i ( t ) G X_{i}(t) GXi?(t) 表示每个候选大猩猩在第 t t t 次迭代时的位置向量, N N N 表示大猩猩个体的总数(种群规模), g g g 由式(9)计算所得;在式(9) 中, L L L 由式(4)计算所得。
1.2.2 竞争成年雌性
如果
C
<
W
C<W
C<W ,则选择开发阶段的第二个机制。一段时间后,当年轻的大猩猩进入青春期时,它们会与其他雄性大猩猩在选择成年?性的 问题上展开竞争,这种竞争通常是激烈的。式(10)模拟了这种行为。
G
X
(
i
)
=
X
silverback?
?
(
X
silverback?
×
Q
?
X
(
t
)
×
Q
)
×
A
(10)
G X(i)=X_{\text {silverback }}-\left(X_{\text {silverback }} \times Q-X(t) \times Q\right) \times A\tag{10}
GX(i)=Xsilverback???(Xsilverback??×Q?X(t)×Q)×A(10)
Q = 2 × r 5 ? 1 (11) Q=2 \times r_{5}-1 \tag{11} Q=2×r5??1(11)
A = β × E (12) A=\beta \times E \tag{12} A=β×E(12)
E = { N 1 , ?rand? ≥ 0.5 N 2 , ?rand? < 0.5 (13) E= \begin{cases}N_{1}, & \text { rand } \geq 0.5 \\ N_{2}, & \text { rand }<0.5\end{cases} \tag{13} E={N1?,N2?,??rand?≥0.5?rand?<0.5?(13)
其中, X silverback? X_{\text {silverback }} Xsilverback?? 为银背大猩猩的位置向量(最佳位置), X ( t ) X(t) X(t) 为当前大猩猩个体的位置向量, Q Q Q 用于模拟冲击力, r 5 r_{5} r5? 是0到1间的随机值, A A A为冲突中暴力程度的系数向量 ; β \beta β 是在优化操作之前给定的参数值, E E E 使用式(13)进行评估,同时用于模拟暴力对解决方案维度的影响。如果 r a n d ≥ 0.5 , r a n d \geq 0.5 , rand≥0.5, 则 E E E 的值将等于正态分布和问题维度 中的随机值;但如果 r a n d < 0.5 rand <0.5 rand<0.5 , E E E 将等于正态分布中的随机值。rand是介于 0 和1之间的随机值。在开发阶段结束时,进行一次群体操作,在该操作中,估计所有 G X G X GX 个体的适应度值,如果适应度值满足 G X ( t ) < X ( t ) G X(t)<X(t) GX(t)<X(t) ,则使用 G X ( t ) G X(t) GX(t) 作为 X ( t ) X(t) X(t) 个体,并将在整个种群中获得的最佳解视为银背大猩猩。
算法伪代码如下:
% GTO setting
Inputs: The population sizeNand maximum number of iterationsTand parameters β and p
Outputs: The location of Gorilla and its fitness value
% initialization
Initialize the random populationX i N( = 1 , 2 , , )…i
Calculate the fitness values of Gorilla
% Main Loop
while (stopping condition is not met) do
Update theCusing Equation (2)
Update theLusing Equation (4)
% Exploration phase
for (each Gorilla (Xi)) do
Update the location Gorilla using Equation (1)
end for
% Create group
Calculate the fitness values of Gorilla
if GX is better than X, replace them
Set Xsilverback as the location of silverback(best location)
% Exploitation phase
for (each Gorilla (Xi)) do
if (|C|>=1) then
Update the location Gorilla using Equation (7)
Else
Update the location Gorilla using Equation (10)
End if
end for
% Create group
Calculate the fitness values of Gorilla
if New Solutions are better than previous solutions, replace them
Set Xsilverback as the location of silverback(best location)
end while
Return XBestGorilla, bestFitness
2.实验结果
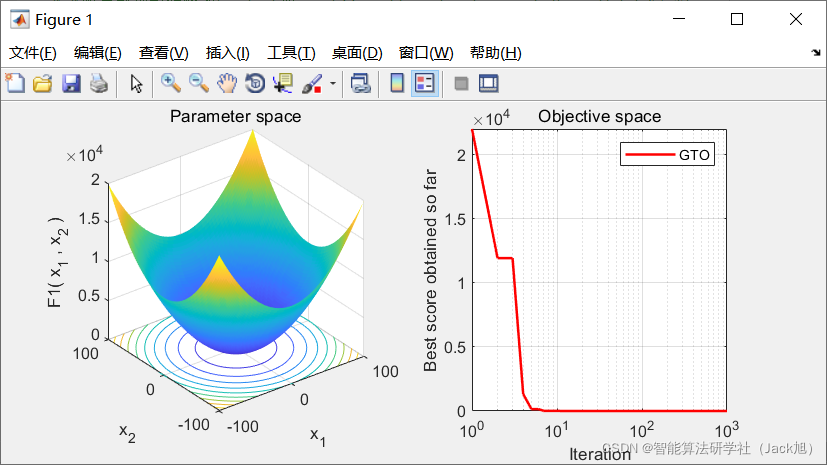
3.参考文献
[1] Abdollahzadeh B , Gharehchopogh F S , Mirjalili S . Artificial gorilla troops optimizer: A new nature-inspired metaheuristic algorithm for global optimization problems[J]. International Journal of Intelligent Systems.
4.Matlab
ure-inspired metaheuristic algorithm for global optimization problems[J]. International Journal of Intelligent Systems.