给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。

思路:二分、双指针
中位数:我们分别找第 (m+n+1) / 2 个,和 (m+n+2) / 2 个,然后求其平均值即可,这对奇偶数均适用
这里我们需要定义一个函数来在两个有序数组中找到第K个元素,
- 首先,使用两个变量 i 和 j 分别来标记数组nums1和nums2的起始位置。
- 边界条件:
①当某一个数组的起始位置 i 大于等于其数组长度时,说明其所有数字均已经被淘汰了,相当于一个空数组了,那么实际上就变成了在另一个数组中找数字。
②如果K=1的话,那么我们只要比较nums1和nums2的起始位置 i 和 j 上的数字就可以了。 - 使用二分法,对 K 二分,分别在nums1和nums2中查找第
K/2个元素(需要先检查数组中到底存不存在第 K/2 个数字)
①如果存在就取出来,否则就赋值上一个整型最大值。
②如果某个数组不存在第K/2个数字,那么我们就淘汰另一个数组的前K/2个数字即可。 - 二分法的核心啦,比较这两个数组的第
K/2小的数字midVal1和midVal2的大小,如果midVal1小的话,则说明数组1中的前 k/2 个元素不可能成为第 k 个元素的候选,所以我们可以将其淘汰,①将nums1的起始位置向后移动K/2个,②并且此时的K也自减去K/2,调用递归。反之,我们淘汰nums2中的前K/2个数字,并将nums2的起始位置向后移动K/2个,并且此时的K也自减去K/2,调用递归即可。

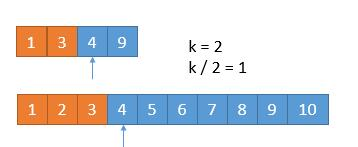
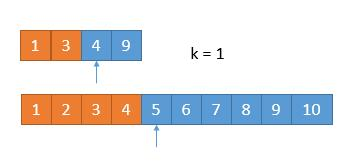
哪个小,就表明该数组的前 k/2 个数字都不是第 k 小数字,所以可以排除。也就是 1,2,3 这三个数字不可能是第 7 小的数字。将 1349 和 45678910 两个数组作为新的数组进行比较。
数组2起始位置向后移 k/2,k 也减去 k/2

class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int m = nums1.length;
int n = nums2.length;
int left = (m + n + 1) / 2;
int right = (m + n + 2) / 2;
return (findKth(nums1, 0, nums2, 0, left) + findKth(nums1, 0, nums2, 0, right)) / 2.0;
}
//i: nums1的起始位置;j: nums2的起始位置;k:找第k个值
public int findKth(int[] nums1, int i, int[] nums2, int j, int k){
if( i >= nums1.length) return nums2[j + k - 1];//nums1为空数组
if( j >= nums2.length) return nums1[i + k - 1];//nums2为空数组
if(k==1) return Math.min(nums1[i], nums2[j]);
int midVal1 = (i + k / 2 - 1 < nums1.length) ? nums1[i + k / 2 - 1] : Integer.MAX_VALUE;
int midVal2 = (j + k / 2 - 1 < nums2.length) ? nums2[j + k / 2 - 1] : Integer.MAX_VALUE;
if(midVal1 < midVal2){
return findKth(nums1, i + k / 2, nums2, j , k - k / 2);
}else{
return findKth(nums1, i, nums2, j + k / 2 , k - k / 2);
}
}
}