[数据结构与算法]字符串匹配 (KMP)

字符串匹配

在常见的字符串相关的算法问题中有一种较为常见的是匹配问题,分为单模匹配与多模匹配,
多是要求我们在时限内计算单个或多个模式串在很长的一串原文串中的出现情况
单模匹配最好想到的就是时间复杂度O(n*m)的暴风(bf)算法,而当n和m是1e5量级的时候bf算法容易超时,
故而Knuth , Morris 和 Pratt 三人研究出了一种更加优秀的时间复杂度O(n+m)的算法去三人名称首字母
命名为KMP算法,自此单模匹配问题得到解决.
更难的多模匹配问题是通过AC自动机解决的,AC自动机简单的说就是利用字典树存储所有模式串,并使用KMP思
路在字典树上构造失败跳转指针,在匹配时将原文串与字典树进行模式匹配

字符串匹配暴力

void bf(const char*a,const char*b){
    int i=0,j,ans=0;
    while(a[i]){
        j = 0;
        while(b[j]&&a[i+j]==b[j])
            j++;
        if(!b[j])
            printf("原串%d下标位置匹配成功\n", i);
        i++;
    }
}

kmp算法

概念:
KMP是一种时间复杂度O(n+m)的字符串单模匹配算法，核心是通过预处理模式串的所有前缀串的最长相同前后缀，构造next数组，在原串与模式串匹配失败时参考next数组做跳转避免原串指针的回退并减少模式串指针的回退长度。
作用:
KMP算法的作用是在一个已知字符串中查找子串的位置,也叫做串的模式匹配。比如主串s=“goodgoogle”,子串t=“google”。
感谢博主 : https://blog.csdn.net/weixin_46007276/article/details/104372119
预备知识:
字符串 abcdab
前缀的集合：{a,ab,abc,abcd,abcda}
后缀的集合：{b,ab,dab,cdab,bcdab}
那么最长相等前后缀不就是ab嘛.

next[i]数组作用:
1.next[i]的值表示下标为i的字符前的字符串最长相等前后缀的长度。
2.表示该处字符不匹配时应该回溯到的字符的下标
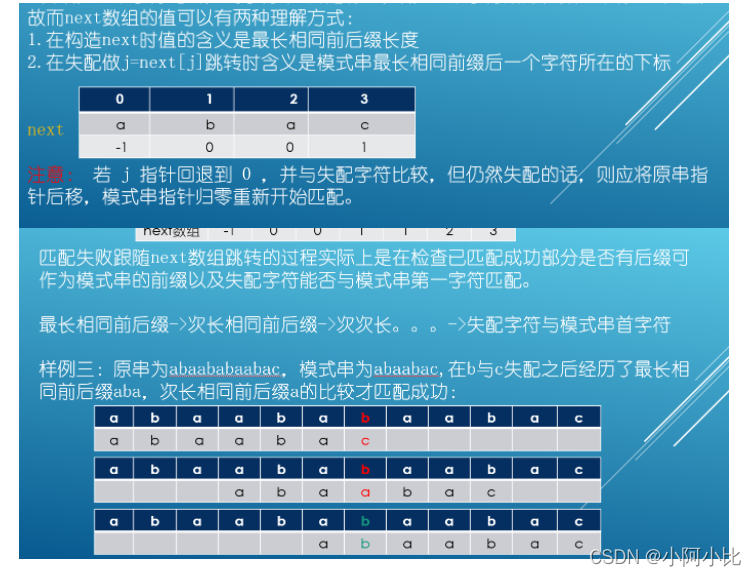
匹配方式以及next[i]数组的作用含义:
在红色位置失配了，j 要重新匹配，那和模式串中哪个字符重新匹配呢？应该是已匹配部分的最长相同前后缀中前缀后一个字符，比如模式串abac当c失配时aba已匹配成功，最长相同前后缀是a，最长相同前缀后一个字符是b，所以原串失配字符下一次应该和b比较，因为我们的已匹配成功部分若想成为新的匹配成功情况的一部分必然是某后缀作为了模式串的前缀。
比如已匹配部分的最长相同前后缀长度若为x，则原串失配字符下一次就该与模式串第x+1个字符比对，而字符串0开始存的，第x+1个字符刚好在数组下标x的位置

next[i]数组的实现

实现逻辑:
next数组实现逻辑：
0下标对应的next值设置为某负数，因为next数组含义为最长相同前后缀长度，长度不可能为负数，故而实际上这是一个特殊值，因为若是连模式串的第一个字符都与失配位置没匹配上，则需要一个特殊值提醒原串指针后移模式串重新开始匹配。
然后从左到右推算每个位置的next值，用一个j记录当前[0,i)部分的最长相同前后缀长度，比较最长相同前缀后一个字符s[j]与新字符s[i]是否相同，相同则前后缀得到增长，否则j=next[j]比较次长相同前缀后一个字符是否与s[i]相同,直到j退为负数特殊值。将next值赋为0。

next[]数组的优化
这种情况出现的原因是当你的next数组回退之后，回退的字符与当前失配的模式串字符一样，那么这次匹配依旧会发生适配现象，所以在每次填入新的Next数组时，将其回退的字符与当前字符匹配一下，当字符一样的时候，再次跳转至上一个Next,
优化的作用是重新赋值next数组,.使匹配的速度更快

kmp算法实现

void getnext(char* s){
    int i=0,j=-1;
    next[i]=j;
    while(s[i]){//该条件为判断数组是否为空,可以根据题意改变
        if(j==-1||s[i]==s[j]){
            next[++i]=++j;
            if(s[i]==s[next[i]]){//优化这种情况出现的原因是当你的next数组回退之后，回退的
                next[i]==next[next[i]];//字符与当前失配的模式串字符一样，那么这次匹配依旧会发生适配现
            }//象，所以在每次填入新的Next数组时，将其回退的字符与当前
        }//字符匹配一下，当字符一样的时候，再次跳转至上一个Next
        else j=next[j];
    }
}
void kmp(char* a,char *b){
    getnext(b);
    int i=0,j=0,ans=0;
    while(a[i]){
        if(j==-1||a[i]==b[j]){
            i++,j++;
            if(!b[j]){//判断j加一后如果b数组到头了
                printf("原串%d位置匹配成功\n",i-strlen(b));
                ans++;//匹配成功的次数
                j=next[j];//跳回到上一个最长相同前后缀
            }
        }
        else j=next[j];
    }
}

kmp模板

next[i]数组作用:
1.next[i]的值表示下标为i的字符前的字符串最长相等前后缀的长度。
2.表示该处字符不匹配时应该回溯到的字符的下标
KMP字符串
给定一个模式串 S，以及一个模板串P，所有字符串中只包含大小写英文字母以及阿拉伯数字。
模板串 P 在模式串 S 中多次作为子串出现。
求出模板串 P 在模式串 S 中所有出现的位置的起始下标。
输入格式
第一行输入整数 N，表示字符串 P 的长度。
第二行输入字符串 P。
第三行输入整数 MM，表示字符串 S 的长度。
第四行输入字符串 S。
输出格式
共一行，输出所有出现位置的起始下标（下标从 0 开始计数），整数之间用空格隔开。
数据范围
1≤N≤105
1≤M≤106
输入样例：

3
aba
5
ababa

输出样例：

0 2

AC代码
** 数组从1开始存储 ,然后ne数组匹配答案串,ne[1]=0,然后ne数组中的i表示前i位可以匹配的相同前后缀,j的坐标每次都比i小1 **

#include <iostream>

using namespace std;
const int N = 100010, M = 1000010;

int n, m;
int ne[N];
char s[M], p[N];

int main(){
    cin >> n >> p + 1 >> m >> s + 1;//下标均从1开始

    for (int i = 2, j = 0; i <= n; i ++ ){ //j表示匹配成功的长度,i表示p数组中的下标,因为p数组的下标是从1开始的,只有1个时,一定为0,所以i从2开始
        while (j && p[i] != p[j + 1]) j = ne[j];
        //如果不行可以换到next数组
        if (p[i] == p[j + 1]) j ++ ;
        //成功了就加1
        ne[i] = j;//得到ne数组的值
        //对应其下标
    }

    for (int i = 1, j = 0; i <= m; i ++ ){
        while (j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j ++ ;
        if (j == n){
            printf("%d ", i - n);//第一次匹配成功的位置 
            j = ne[j];//然后回跳,接着找 
        }
    }

    return 0;
}