[数据结构与算法]队列和链表（二）

一、队列

1. 队列是一个有序列表，可以用数组或是链表来实现。
2. 遵循先入先出的原则。即：先存入队列的数据，要先取出。后存入的要后取出

1.1数组模拟队列

• 队列本身是有序列表，若使用数组的结构来存储队列的数据，则队列数组的声明如下图, 其中 maxSize 是该队 列的最大容量。
• 因为队列的输出、输入是分别从前后端来处理，因此需要两个变量 front 及 rear 分别记录队列前后端的下标， front
  会随着数据输出而改变，而 rear 则是随着数据输入而改变，如图所示:
  
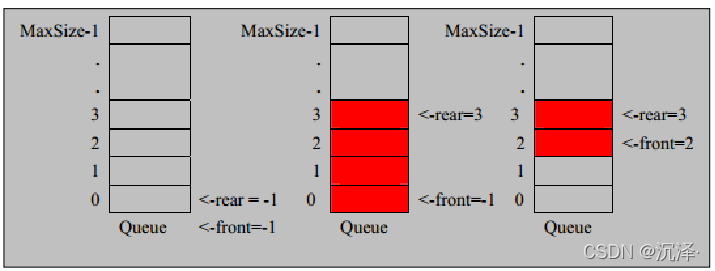
  当我们将数据存入队列时称为”addQueue”，addQueue 的处理需要有两个步骤：思路分析

1. 将尾指针往后移：rear+1 , 当 front == rear 时队列为空
2. 若尾指针 rear 小于队列的最大下标 maxSize-1，则将数据存入 rear 所指的数组元素中；否则无法存入数据。即 rear == maxSize - 1队列满

代码实现：

// 使用数组模拟队列-编写一个ArrayQueue类
class ArrayQueue {
	private int maxSize; // 表示数组的最大容量
	private int front; // 队列头
	private int rear; // 队列尾
	private int[] arr; // 该数据用于存放数据, 模拟队列

	// 创建队列的构造器
	public ArrayQueue(int arrMaxSize) {
		maxSize = arrMaxSize;
		arr = new int[maxSize];
		front = -1; // 指向队列头部，分析出front是指向队列头的前一个位置.
		rear = -1; // 指向队列尾，指向队列尾的数据(即就是队列最后一个数据)
	}

	// 判断队列是否满
	public boolean isFull() {
		return rear == maxSize - 1;
	}

	// 判断队列是否为空
	public boolean isEmpty() {
		return rear == front;
	}

	// 添加数据到队列
	public void addQueue(int n) {
		// 判断队列是否满
		if (isFull()) {
			System.out.println("队列满，不能加入数据~");
			return;
		}
		rear++; // 让rear 后移
		arr[rear] = n;
	}

	// 获取队列的数据, 出队列
	public int getQueue() {
		// 判断队列是否空
		if (isEmpty()) {
			// 通过抛出异常
			throw new RuntimeException("队列空，不能取数据");
		}
		front++; // front后移
		return arr[front];

	}

	// 显示队列的所有数据
	public void showQueue() {
		// 遍历
		if (isEmpty()) {
			System.out.println("队列空的，没有数据~~");
			return;
		}
		for (int i = 0; i < arr.length; i++) {
			System.out.printf("arr[%d]=%d\n", i, arr[i]);
		}
	}

	// 显示队列的头数据， 注意不是取出数据
	public int headQueue() {
		// 判断
		if (isEmpty()) {
			throw new RuntimeException("队列空的，没有数据~~");
		}
		return arr[front + 1];
	}
}

问题分析并优化

1. 目前数组使用一次就不能用， 没有达到复用的效果
2. 将这个数组使用算法，改进成一个环形的队列 取模：%

1.2数组模拟环形队列

对前面的数组模拟队列的优化，充分利用数组. 因此将数组看做是一个环形的。(通过取模的方式来实现即可)

分析说明：

1. 尾索引的下一个为头索引时表示队列满，即将队列容量空出一个作为约定,这个在做判断队列满的 时候需要注意 (rear + 1) % maxSize == front [满]
2. rear == front [空]
3. 分析示意图:
   

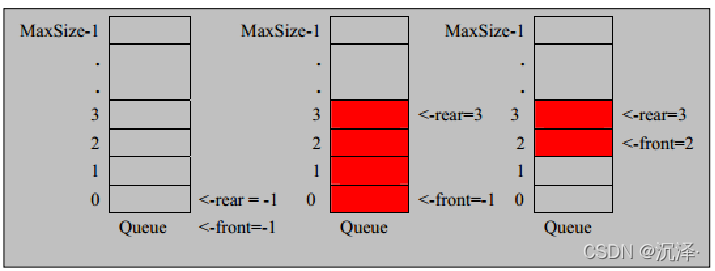
思路如下:
1.front变量的含义做一个调整: front就指向队列的第一个元素,也就是说arr[front]就是队列的第一个元素front的初始值=0
2. rear变量的含义做一个调整;rear指向队列的最后一个元素的后一个位置.因为希望空出一个空间做为约定.rear的初始值=0
3.当队列满时,条件是(rear+1) %maxsize = front【满】
4.对队列为空的条件,rear == front空
5.当我们这样分析，队列中有效的数据的个数(rear+ maxSize - front) % maxSize // rear=1 front =0
6.我们就可以在原来的队列上修改得到,一个环形队列

代码实现：

class CircleArray {
	private int maxSize; // 表示数组的最大容量
	//front 变量的含义做一个调整： front 就指向队列的第一个元素, 也就是说 arr[front] 就是队列的第一个元素 
	//front 的初始值 = 0
	private int front; 
	//rear 变量的含义做一个调整：rear 指向队列的最后一个元素的后一个位置. 因为希望空出一个空间做为约定.
	//rear 的初始值 = 0
	private int rear; // 队列尾
	private int[] arr; // 该数据用于存放数据, 模拟队列
	
	public CircleArray(int arrMaxSize) {
		maxSize = arrMaxSize;
		arr = new int[maxSize];
	}
	
	// 判断队列是否满
	public boolean isFull() {
		return (rear  + 1) % maxSize == front;
	}
	
	// 判断队列是否为空
	public boolean isEmpty() {
		return rear == front;
	}
	
	// 添加数据到队列
	public void addQueue(int n) {
		// 判断队列是否满
		if (isFull()) {
			System.out.println("队列满，不能加入数据~");
			return;
		}
		//直接将数据加入
		arr[rear] = n;
		//将 rear 后移, 这里必须考虑取模
		rear = (rear + 1) % maxSize;
	}
	
	// 获取队列的数据, 出队列
	public int getQueue() {
		// 判断队列是否空
		if (isEmpty()) {
			// 通过抛出异常
			throw new RuntimeException("队列空，不能取数据");
		}
		// 这里需要分析出 front是指向队列的第一个元素
		// 1. 先把 front 对应的值保留到一个临时变量
		// 2. 将 front 后移, 考虑取模
		// 3. 将临时保存的变量返回
		int value = arr[front];
		front = (front + 1) % maxSize;
		return value;

	}
	
	// 显示队列的所有数据
	public void showQueue() {
		// 遍历
		if (isEmpty()) {
			System.out.println("队列空的，没有数据~~");
			return;
		}
		// 思路：从front开始遍历，遍历多少个元素
		// 动脑筋
		for (int i = front; i < front + size() ; i++) {
			System.out.printf("arr[%d]=%d\n", i % maxSize, arr[i % maxSize]);
		}
	}
	
	// 求出当前队列有效数据的个数
	public int size() {
		// rear = 2
		// front = 1
		// maxSize = 3 
		return (rear + maxSize - front) % maxSize;   
	}
	
	// 显示队列的头数据， 注意不是取出数据
	public int headQueue() {
		// 判断
		if (isEmpty()) {
			throw new RuntimeException("队列空的，没有数据~~");
		}
		return arr[front];
	}
}

二、链表

链表是有序的列表，但是它在内存中是存储如下：

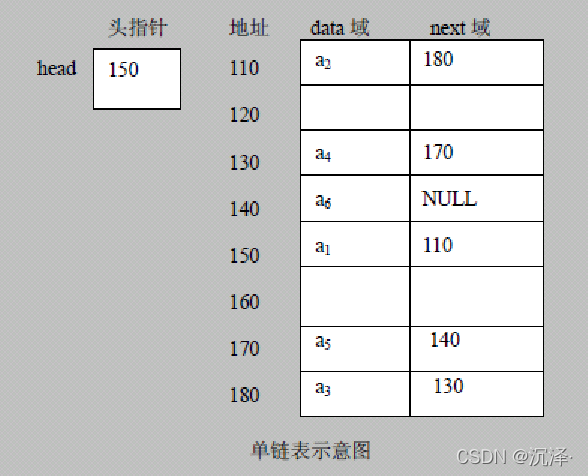
小结上图:

1. 链表是以节点的方式来存储,是链式存储
2. 每个节点包含 data 域， next 域：指向下一个节点.
3. 如图：发现链表的各个节点不一定是连续存储.
4. 链表分带头节点的链表和没有头节点的链表，根据实际的需求来确定

2.1 单链表

单链表(带头结点) 逻辑结构示意图如下

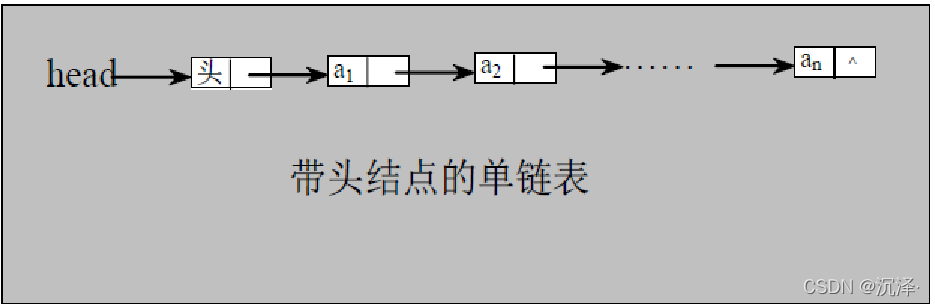
示例：使用带 head 头的单向链表实现 –水浒英雄排行榜管理完成对英雄人物的增删改查操作， 注:新增、 删除和修改,查找

1、第一种方法在添加英雄时，直接添加到链表的尾部：

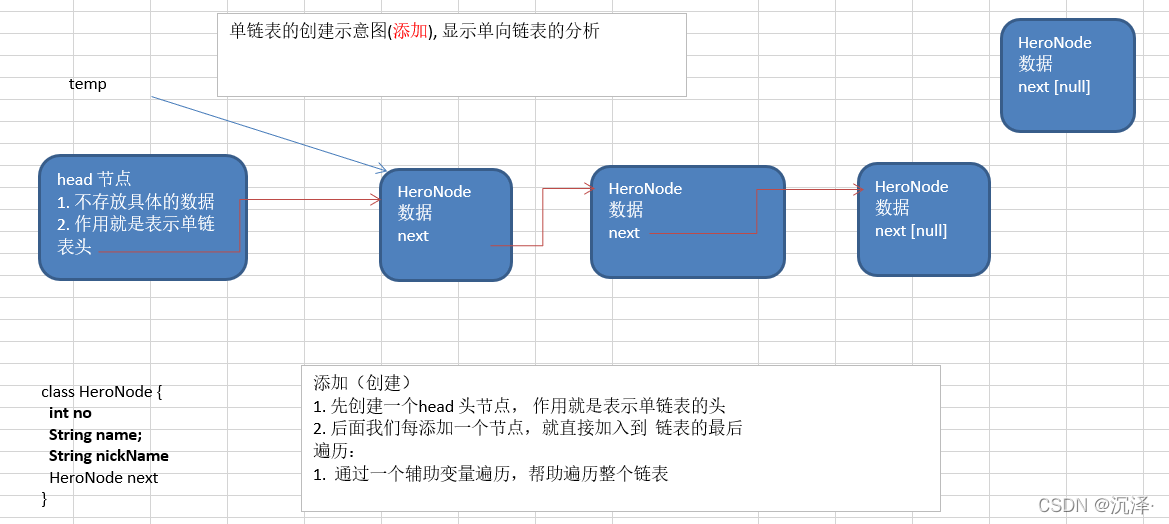
2、第二种方式在添加英雄时，根据排名将英雄插入到指定位置(如果有这个排名，则添加失败，并给出提示) 思路的分析示意图:

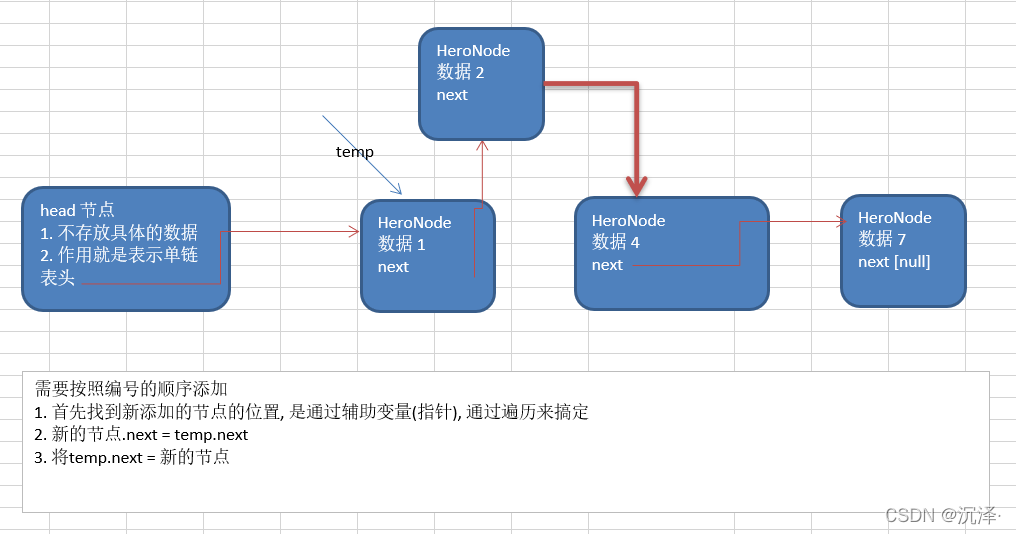
3、 修改节点功能 思路
先找到该节点，通过遍历
temp.name = newHeroNode.name ;
temp.nickname= newHeroNode.nickname

4、删除节点 思路分析的示意图

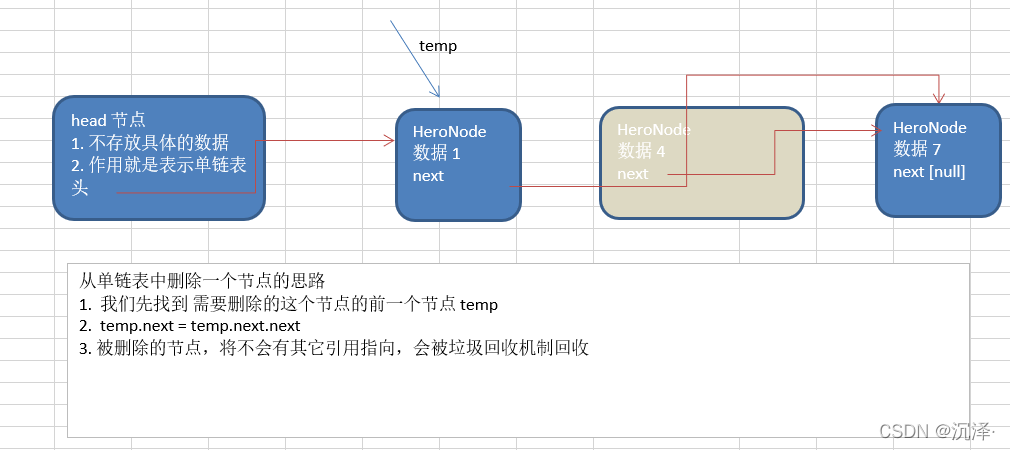
//定义SingleLinkedList 管理我们的英雄
class SingleLinkedList {
	//先初始化一个头节点, 头节点不要动, 不存放具体的数据
	private HeroNode head = new HeroNode(0, "", "");
	
	
	//返回头节点
	public HeroNode getHead() {
		return head;
	}

	//添加节点到单向链表
	//思路，当不考虑编号顺序时
	//1. 找到当前链表的最后节点
	//2. 将最后这个节点的next 指向 新的节点
	public void add(HeroNode heroNode) {
		
		//因为head节点不能动，因此我们需要一个辅助遍历 temp
		HeroNode temp = head;
		//遍历链表，找到最后
		while(true) {
			//找到链表的最后
			if(temp.next == null) {//
				break;
			}
			//如果没有找到最后, 将将temp后移
			temp = temp.next;
		}
		//当退出while循环时，temp就指向了链表的最后
		//将最后这个节点的next 指向 新的节点
		temp.next = heroNode;
	}
	
	//第二种方式在添加英雄时，根据排名将英雄插入到指定位置
	//(如果有这个排名，则添加失败，并给出提示)
	public void addByOrder(HeroNode heroNode) {
		//因为头节点不能动，因此我们仍然通过一个辅助指针(变量)来帮助找到添加的位置
		//因为单链表，因为我们找的temp 是位于 添加位置的前一个节点，否则插入不了
		HeroNode temp = head;
		boolean flag = false; // flag标志添加的编号是否存在，默认为false
		while(true) {
			if(temp.next == null) {//说明temp已经在链表的最后
				break; //
			} 
			if(temp.next.no > heroNode.no) { //位置找到，就在temp的后面插入
				break;
			} else if (temp.next.no == heroNode.no) {//说明希望添加的heroNode的编号已然存在
				
				flag = true; //说明编号存在
				break;
			}
			temp = temp.next; //后移，遍历当前链表
		}
		//判断flag 的值
		if(flag) { //不能添加，说明编号存在
			System.out.printf("准备插入的英雄的编号 %d 已经存在了, 不能加入\n", heroNode.no);
		} else {
			//插入到链表中, temp的后面
			heroNode.next = temp.next;
			temp.next = heroNode;
		}
	}

	//修改节点的信息, 根据no编号来修改，即no编号不能改.
	//说明
	//1. 根据 newHeroNode 的 no 来修改即可
	public void update(HeroNode newHeroNode) {
		//判断是否空
		if(head.next == null) {
			System.out.println("链表为空~");
			return;
		}
		//找到需要修改的节点, 根据no编号
		//定义一个辅助变量
		HeroNode temp = head.next;
		boolean flag = false; //表示是否找到该节点
		while(true) {
			if (temp == null) {
				break; //已经遍历完链表
			}
			if(temp.no == newHeroNode.no) {
				//找到
				flag = true;
				break;
			}
			temp = temp.next;
		}
		//根据flag 判断是否找到要修改的节点
		if(flag) {
			temp.name = newHeroNode.name;
			temp.nickname = newHeroNode.nickname;
		} else { //没有找到
			System.out.printf("没有找到 编号 %d 的节点，不能修改\n", newHeroNode.no);
		}
	}
	
	//删除节点
	//思路
	//1. head 不能动，因此我们需要一个temp辅助节点找到待删除节点的前一个节点
	//2. 说明我们在比较时，是temp.next.no 和  需要删除的节点的no比较
	public void del(int no) {
		HeroNode temp = head;
		boolean flag = false; // 标志是否找到待删除节点的
		while(true) {
			if(temp.next == null) { //已经到链表的最后
				break;
			}
			if(temp.next.no == no) {
				//找到的待删除节点的前一个节点temp
				flag = true;
				break;
			}
			temp = temp.next; //temp后移，遍历
		}
		//判断flag
		if(flag) { //找到
			//可以删除
			temp.next = temp.next.next;
		}else {
			System.out.printf("要删除的 %d 节点不存在\n", no);
		}
	}
	
	//显示链表[遍历]
	public void list() {
		//判断链表是否为空
		if(head.next == null) {
			System.out.println("链表为空");
			return;
		}
		//因为头节点，不能动，因此我们需要一个辅助变量来遍历
		HeroNode temp = head.next;
		while(true) {
			//判断是否到链表最后
			if(temp == null) {
				break;
			}
			//输出节点的信息
			System.out.println(temp);
			//将temp后移， 一定小心
			temp = temp.next;
		}
	}
}

//定义HeroNode ， 每个HeroNode 对象就是一个节点
class HeroNode {
	public int no;
	public String name;
	public String nickname;
	public HeroNode next; //指向下一个节点
	//构造器
	public HeroNode(int no, String name, String nickname) {
		this.no = no;
		this.name = name;
		this.nickname = nickname;
	}
	//为了显示方法，我们重新toString
	@Override
	public String toString() {
		return "HeroNode [no=" + no + ", name=" + name + ", nickname=" + nickname + "]";
	}
	
}

2.1.1 求单链表中有效节点的个数

方法：获取到单链表的节点的个数(如果是带头结点的链表，需求不统计头节点)

/**
	 * 
	 * @param head 链表的头节点
	 * @return 返回的就是有效节点的个数
	 */
	public static int getLength(HeroNode head) {
		if(head.next == null) { //空链表
			return 0;
		}
		int length = 0;
		//定义一个辅助的变量, 这里我们没有统计头节点
		HeroNode cur = head.next;
		while(cur != null) {
			length++;
			cur = cur.next; //遍历
		}
		return length;
	}

2.1.2 查找单链表中的倒数第 k 个结点

思路：
//1. 编写一个方法，接收head节点，同时接收一个index
//2. index 表示是倒数第index个节点
//3. 先把链表从头到尾遍历，得到链表的总的长度 getLength
//4. 得到size 后，我们从链表的第一个开始遍历 (size-index)个，就可以得到
//5. 如果找到了，则返回该节点，否则返回nulll

	public static HeroNode findLastIndexNode(HeroNode head, int index) {
		//判断如果链表为空，返回null
		if(head.next == null) {
			return null;//没有找到
		}
		//第一个遍历得到链表的长度(节点个数)
		int size = getLength(head);
		//第二次遍历  size-index 位置，就是我们倒数的第K个节点
		//先做一个index的校验
		if(index <=0 || index > size) {
			return null; 
		}
		//定义给辅助变量， for 循环定位到倒数的index
		HeroNode cur = head.next; //3 // 3 - 1 = 2
		for(int i =0; i< size - index; i++) {
			cur = cur.next;
		}
		return cur;
		
	}

2.1.3 单链表的反转

思路分析图解

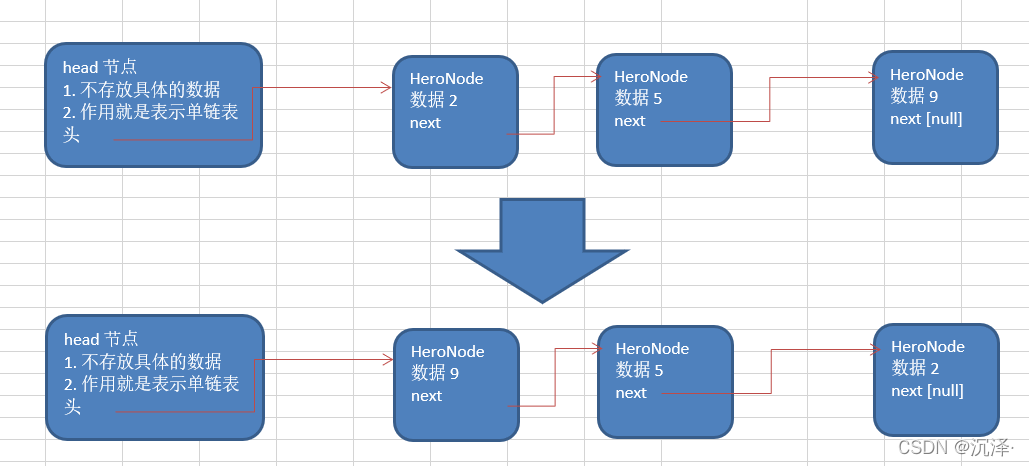
public static void reversetList(HeroNode head) {
		//如果当前链表为空，或者只有一个节点，无需反转，直接返回
		if(head.next == null || head.next.next == null) {
			return ;
		}
		
		//定义一个辅助的指针(变量)，帮助我们遍历原来的链表
		HeroNode cur = head.next;
		HeroNode next = null;// 指向当前节点[cur]的下一个节点
		HeroNode reverseHead = new HeroNode(0, "", "");
		//遍历原来的链表，每遍历一个节点，就将其取出，并放在新的链表reverseHead 的最前端
		//动脑筋
		while(cur != null) { 
			next = cur.next;//先暂时保存当前节点的下一个节点，因为后面需要使用
			
			cur.next = reverseHead.next;//将cur的下一个节点指向新的链表的最前端
			reverseHead.next = cur; //将cur 连接到新的链表上
			
			cur = next;//让cur后移
		}
		//将head.next 指向 reverseHead.next , 实现单链表的反转
		head.next = reverseHead.next;
	}

2.1.4 从尾到头打印单链表

思路

• 方式1:先将单链表进行反转操作，然后再逾预今这样的做的问题是会破坏原来的单链表的结构，不建议
• 方式2:可以利用找这个数据结构，将各个节点压火到栈中，然后利用栈的先进后出的特点,就实现了逆序打印的效果.

举例演示柱的使用stack：

//演示栈Stack的基本使用
public class TestStack {

	public static void main(String[] args) {
		Stack<String> stack = new Stack();
		// 入栈
		stack.add("jack");
		stack.add("tom");
		stack.add("smith");

		// 出栈
		// smith, tom , jack
		while (stack.size() > 0) {
			System.out.println(stack.pop());//pop就是将栈顶的数据取出
		}
	}

}

单链表的逆序打印代码：

	//可以利用栈这个数据结构，将各个节点压入到栈中，然后利用栈的先进后出的特点，就实现了逆序打印的效果
	public static void reversePrint(HeroNode head) {
		if(head.next == null) {
			return;//空链表，不能打印
		}
		//创建要给一个栈，将各个节点压入栈
		Stack<HeroNode> stack = new Stack<HeroNode>();
		HeroNode cur = head.next;
		//将链表的所有节点压入栈
		while(cur != null) {
			stack.push(cur);
			cur = cur.next; //cur后移，这样就可以压入下一个节点
		}
		//将栈中的节点进行打印,pop 出栈
		while (stack.size() > 0) {
			System.out.println(stack.pop()); //stack的特点是先进后出
		}
	}

2.1.5 合并两个有序的单链表，合并之后的链表依然有序

package com.atguigu.test;

public class Test {
    public static void main(String[] args) {
        System.out.println("************");
        Node link1 = new Node(null, "");
        Node a1 = new Node(1, "a1");
        Node a3 = new Node(3, "a3");
        Node a5 = new Node(5, "a5");
        link1.next = a1;
        a1.next = a3;
        a3.next = a5;
        Node link2 = new Node(null, "");
        Node a2 = new Node(2, "a2");
        Node a4 = new Node(4, "a4");
        Node a6 = new Node(6, "a6");
        Node a8 = new Node(8, "a8");
        link2.next = a2;
        a2.next = a4;
        a4.next = a6;
        a6.next = a8;
        Node node = mergeLink(link1, link2);
    }

    public static Node mergeLink(Node link1, Node link2) {
        if (link1 == null || link1.next == null) {
            return link2;
        }
        if (link2 == null || link2.next == null) {
            return link1;
        }
        Node newLink = new Node(null, "");
        Node cur1 = link1.next;
        Node cur2 = link2.next;
        while (cur1 != null && cur2 != null) {
            if (cur1.no <= cur2.no) {
                Node temp = new Node(cur1.no, cur1.name);
                temp.next = newLink.next;
                newLink.next = temp;
                cur1 = cur1.next;
            } else {
                Node temp = new Node(cur2.no, cur2.name);
                temp.next = newLink.next;
                newLink.next = temp;
                cur2 = cur2.next;
            }
        }
        while (cur2 != null){
            Node temp = new Node(cur2.no, cur2.name);
            temp.next = newLink.next;
            newLink.next = temp;
            cur2 = cur2.next;
        }
        while (cur1 != null){
            Node temp = new Node(cur1.no, cur1.name);
            temp.next = newLink.next;
            newLink.next = temp;
            cur1 = cur1.next;
        }
        return newLink;
    }

}
class Node {
    Integer no;
    String name;
    Node next;
    public Node(Integer no, String name) {
        this.no = no;
        this.name = name;
    }
}

合并成新的有序链表，一般要创建新的节点，想通过改变原有链表节点指向实现，相对较复杂。

2.2 双向链表

管理单向链表的缺点分析:

1. 单向链表，查找的方向只能是一个方向，而双向链表可以向前或者向后查找。
2. 单向链表不能自我删除，需要靠辅助节点 ，而双向链表，则可以自我删除，所以前面我们单链表删除 时节点，总是找到 temp,temp 是待删除节点的前一个节点(认真体会).

使用带 head 头的双向链表实现 –水浒英雄排行榜，分析双向链表如何完成遍历，添加，修改和删除的思路

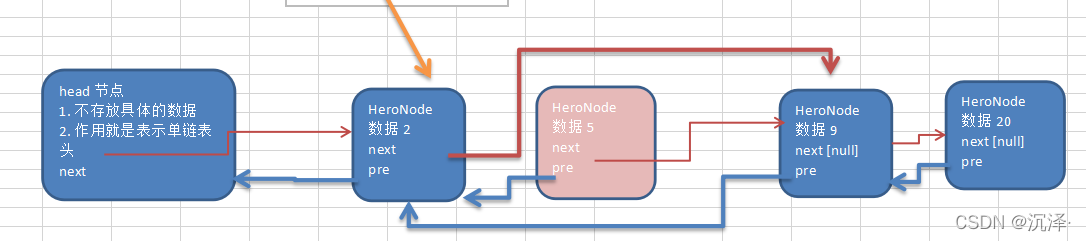
对上图的说明:
分析 双向链表的遍历，添加，修改，删除的操作思路===》代码实现
1、 遍历 方和 单链表一样，只是可以向前，也可以向后查找
2、 添加 (默认添加到双向链表的最后)

(1) 先找到双向链表的最后这个节点
(2) temp.next = newHeroNode
(3) newHeroNode.pre = temp;

3、 修改 思路和 原来的单向链表一样.
4、 删除

(1) 因为是双向链表，因此，我们可以实现自我删除某个节点
(2) 直接找到要删除的这个节点，比如 temp
(3) temp.pre.next = temp.next
(4) temp.next.pre = temp.pre;

代码实现：

// 创建一个双向链表的类
class DoubleLinkedList {

	// 先初始化一个头节点, 头节点不要动, 不存放具体的数据
	private HeroNode2 head = new HeroNode2(0, "", "");

	// 返回头节点
	public HeroNode2 getHead() {
		return head;
	}

	// 遍历双向链表的方法
	// 显示链表[遍历]
	public void list() {
		// 判断链表是否为空
		if (head.next == null) {
			System.out.println("链表为空");
			return;
		}
		// 因为头节点，不能动，因此我们需要一个辅助变量来遍历
		HeroNode2 temp = head.next;
		while (true) {
			// 判断是否到链表最后
			if (temp == null) {
				break;
			}
			// 输出节点的信息
			System.out.println(temp);
			// 将temp后移， 一定小心
			temp = temp.next;
		}
	}

	// 添加一个节点到双向链表的最后.
	public void add(HeroNode2 heroNode) {

		// 因为head节点不能动，因此我们需要一个辅助遍历 temp
		HeroNode2 temp = head;
		// 遍历链表，找到最后
		while (true) {
			// 找到链表的最后
			if (temp.next == null) {//
				break;
			}
			// 如果没有找到最后, 将将temp后移
			temp = temp.next;
		}
		// 当退出while循环时，temp就指向了链表的最后
		// 形成一个双向链表
		temp.next = heroNode;
		heroNode.pre = temp;
	}

	//第二种方式在添加英雄时，根据排名将英雄插入到指定位置
	public void addByOrder(int no,HeroNode2 heroNode) {
		// 因为head节点不能动，因此我们需要一个辅助遍历 temp
		HeroNode2 temp = head;
		boolean flag = false;// flag标志添加的编号是否存在，默认为false
		// 遍历链表，找到最后
		while (true) {
			if(temp.next == null) {//说明temp已经在链表的最后
				break; //
			}
			if(temp.next.no > heroNode.no) { //位置找到，就在temp的后面插入
				break;
			} else if (temp.next.no == heroNode.no) {//说明希望添加的heroNode的编号已然存在

				flag = true; //说明编号存在
				break;
			}
			temp = temp.next; //后移，遍历当前链表
		}
		
		if (flag){
			System.out.printf("没有找到 编号 %d 的节点，不能修改\n", no);
		}else {
			heroNode.next = temp.next;
			temp.next.pre = heroNode;
			
			temp.next = heroNode;
			heroNode.pre = temp;
			
		}
	}

	// 修改一个节点的内容, 可以看到双向链表的节点内容修改和单向链表一样
	// 只是 节点类型改成 HeroNode2
	public void update(HeroNode2 newHeroNode) {
		// 判断是否空
		if (head.next == null) {
			System.out.println("链表为空~");
			return;
		}
		// 找到需要修改的节点, 根据no编号
		// 定义一个辅助变量
		HeroNode2 temp = head.next;
		boolean flag = false; // 表示是否找到该节点
		while (true) {
			if (temp == null) {
				break; // 已经遍历完链表
			}
			if (temp.no == newHeroNode.no) {
				// 找到
				flag = true;
				break;
			}
			temp = temp.next;
		}
		// 根据flag 判断是否找到要修改的节点
		if (flag) {
			temp.name = newHeroNode.name;
			temp.nickname = newHeroNode.nickname;
		} else { // 没有找到
			System.out.printf("没有找到 编号 %d 的节点，不能修改\n", newHeroNode.no);
		}
	}

	// 从双向链表中删除一个节点,
	// 说明
	// 1 对于双向链表，我们可以直接找到要删除的这个节点
	// 2 找到后，自我删除即可
	public void del(int no) {

		// 判断当前链表是否为空
		if (head.next == null) {// 空链表
			System.out.println("链表为空，无法删除");
			return;
		}

		HeroNode2 temp = head.next; // 辅助变量(指针)
		boolean flag = false; // 标志是否找到待删除节点的
		while (true) {
			if (temp == null) { // 已经到链表的最后
				break;
			}
			if (temp.no == no) {
				// 找到的待删除节点的前一个节点temp
				flag = true;
				break;
			}
			temp = temp.next; // temp后移，遍历
		}
		// 判断flag
		if (flag) { // 找到
			// 可以删除
			// temp.next = temp.next.next;[单向链表]
			temp.pre.next = temp.next;
			// 这里我们的代码有问题?
			// 如果是最后一个节点，就不需要执行下面这句话，否则出现空指针
			if (temp.next != null) {
				temp.next.pre = temp.pre;
			}
		} else {
			System.out.printf("要删除的 %d 节点不存在\n", no);
		}
	}

}

// 定义HeroNode2 ， 每个HeroNode 对象就是一个节点
class HeroNode2 {
	public int no;
	public String name;
	public String nickname;
	public HeroNode2 next; // 指向下一个节点, 默认为null
	public HeroNode2 pre; // 指向前一个节点, 默认为null
	// 构造器

	public HeroNode2(int no, String name, String nickname) {
		this.no = no;
		this.name = name;
		this.nickname = nickname;
	}

	// 为了显示方法，我们重新toString
	@Override
	public String toString() {
		return "HeroNode [no=" + no + ", name=" + name + ", nickname=" + nickname + "]";
	}

}

2.3 单向环形链表

2.3.1 约瑟夫环

Josephu(约瑟夫、约瑟夫环) 问题 Josephu 问题为：设编号为 1，2，… n 的 n 个人围坐一圈，约定编号为 k（1<=k<=n）的人从 1 开始报数，数 到 m 的那个人出列，它的下一位又从 1 开始报数，数到 m 的那个人又出列，依次类推，直到所有人出列为止，由 此产生一个出队编号的序列。

提示：用一个不带头结点的循环链表来处理 Josephu 问题：先构成一个有 n 个结点的单循环链表，然后由 k 结 点起从 1 开始计数，计到 m 时，对应结点从链表中删除，然后再从被删除结点的下一个结点又从 1 开始计数，直 到最后一个结点从链表中删除算法结束。

2.3.2 单向环形链表介绍

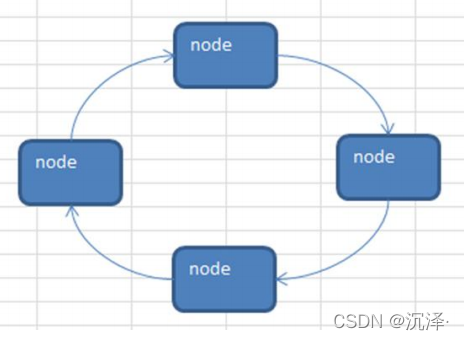
2.3.3 Josephu 问题解决

Josephu 问题为：设编号为1，2，… n的n个人围坐一圈，约定编号为k（1<=k<=n）的人从1开始报数，数到m 的那个人出列，它的下一位又从1开始报数，数到m的那个人又出列，依次类推，直到所有人出列为止，由此产生一个出队编号的序列。

假设：有五人围坐在一起，从第一个人报数，每数两下就有一人出列。
n = 5 , 即有5个人
k = 1, 从第一个人开始报数
m = 2, 数2下

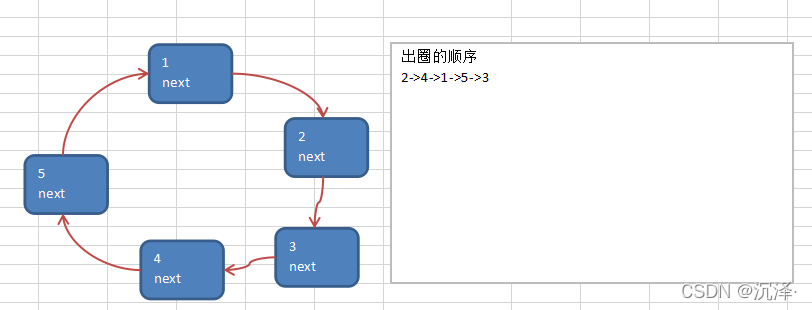
约瑟夫问题-创建环形链表的思路图解：

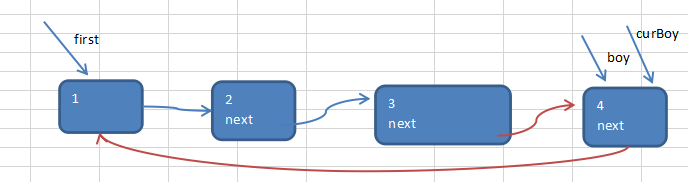
构建一个单向的环形链表思路

1. 先创建第一个节点, 让 first 指向该节点，并形成环形，即first.next=first
2. 后面当我们每创建一个新的节点，就把该节点，加入到已有的环形链表中即可.

遍历环形链表

1. 先让一个辅助指针(变量) curBoy，指向first节点
2. 然后通过一个while循环遍历 该环形链表即可 curBoy.next == first 结束

约瑟夫问题-小孩出圈的思路分析图：

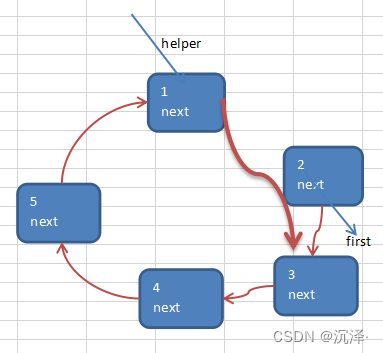
根据用户的输入，生成一个小孩出圈的顺序 n = 5 , 即有5个人 k = 1, 从第一个人开始报数 m = 2, 数2下

1. 需求创建一个辅助指针(变量) helper , 事先应该指向环形链表的最后这个节点. 补充： 小孩报数前，先让 first 和 helper 移动 k - 1次
2. 当小孩报数时，让first 和 helper 指针同时 的移动 m - 1 次
3. 这时就可以将first 指向的小孩节点 出圈 first = first .next helper.next = first;原来first 指向的节点就没有任何引用，就会被回收

出圈的顺序 2->4->1->5->3

// 创建一个环形的单向链表
class CircleSingleLinkedList {
	// 创建一个first节点,当前没有编号
	private Boy first = null;

	// 添加小孩节点，构建成一个环形的链表
	public void addBoy(int nums) {
		// nums 做一个数据校验
		if (nums < 1) {
			System.out.println("nums的值不正确");
			return;
		}
		Boy curBoy = null; // 辅助指针，帮助构建环形链表(为的是不改变first指向第一个小孩)
		// 使用for来创建我们的环形链表
		for (int i = 1; i <= nums; i++) {
			// 根据编号，创建小孩节点
			Boy boy = new Boy(i);
			// 如果是第一个小孩
			if (i == 1) {
				first = boy;
				first.setNext(first); // 构成环
				curBoy = first; // 让curBoy指向第一个小孩
			} else {
				curBoy.setNext(boy);//
				boy.setNext(first);//
				curBoy = boy;
			}
		}
	}

	// 遍历当前的环形链表
	public void showBoy() {
		// 判断链表是否为空
		if (first == null) {
			System.out.println("没有任何小孩~~");
			return;
		}
		// 因为first不能动，因此我们仍然使用一个辅助指针完成遍历
		Boy curBoy = first;
		while (true) {
			System.out.printf("小孩的编号 %d \n", curBoy.getNo());
			if (curBoy.getNext() == first) {// 说明已经遍历完毕
				break;
			}
			curBoy = curBoy.getNext(); // curBoy后移
		}
	}

	// 根据用户的输入，计算出小孩出圈的顺序
	/**
	 * 
	 * @param startNo
	 *            表示从第几个小孩开始数数
	 * @param countNum
	 *            表示数几下
	 * @param nums
	 *            表示最初有多少小孩在圈中
	 */
	public void countBoy(int startNo, int countNum, int nums) {
		// 先对数据进行校验
		if (first == null || startNo < 1 || startNo > nums) {
			System.out.println("参数输入有误， 请重新输入");
			return;
		}
		// 创建要给辅助指针,帮助完成小孩出圈
		Boy helper = first;
		// 需求创建一个辅助指针(变量) helper , 事先应该指向环形链表的最后这个节点
		while (true) {
			if (helper.getNext() == first) { // 说明helper指向最后小孩节点
				break;
			}
			helper = helper.getNext();
		}
		//小孩报数前，先让 first 和  helper 移动 k - 1次
		for(int j = 0; j < startNo - 1; j++) {
			first = first.getNext();
			helper = helper.getNext();
		}
		//当小孩报数时，让first 和 helper 指针同时 的移动  m  - 1 次, 然后出圈
		//这里是一个循环操作，知道圈中只有一个节点
		while(true) {
			if(helper == first) { //说明圈中只有一个节点
				break;
			}
			//让 first 和 helper 指针同时 的移动 countNum - 1
			for(int j = 0; j < countNum - 1; j++) {
				first = first.getNext();
				helper = helper.getNext();
			}
			//这时first指向的节点，就是要出圈的小孩节点
			System.out.printf("小孩%d出圈\n", first.getNo());
			//这时将first指向的小孩节点出圈
			first = first.getNext();
			helper.setNext(first); //
			
		}
		System.out.printf("最后留在圈中的小孩编号%d \n", first.getNo());
		
	}
}

// 创建一个Boy类，表示一个节点
class Boy {
	private int no;// 编号
	private Boy next; // 指向下一个节点,默认null

	public Boy(int no) {
		this.no = no;
	}

	public int getNo() {
		return no;
	}

	public void setNo(int no) {
		this.no = no;
	}

	public Boy getNext() {
		return next;
	}

	public void setNext(Boy next) {
		this.next = next;
	}

}