IT数码 购物 网址 头条 软件 日历 阅读 图书馆
TxT小说阅读器
↓语音阅读,小说下载,古典文学↓ 		图片批量下载器
↓批量下载图片,美女图库↓ 		图片自动播放器
↓图片自动播放器↓ 		一键清除垃圾
↓轻轻一点,清除系统垃圾↓
开发: C++知识库 Java知识库 JavaScript Python PHP知识库 人工智能 区块链 大数据 移动开发 嵌入式 开发工具 数据结构与算法 开发测试 游戏开发 网络协议 系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑 笔记本 显卡 显示器 固态硬盘 硬盘 耳机 手机 iphone vivo oppo 小米 华为 单反 装机 图拉丁
 
   -> 数据结构与算法 -> 【数据结构】学习笔记 -> 正文阅读

[数据结构与算法]【数据结构】学习笔记

数据结构_学习笔记

美好的春节假期结束啦，跟着笔者一起学习数据结构🤪，不要开小china🤘

第 1 章 - 引论

1.1 基本术语

  • 数据

    • 数据是指能够输入到计算机中，并能被计算机处理的一切对象。对计算机科学而言，数据的含义极为广泛,如整数、实数、字符、文字、图形、图像和声音等都是数据。

  • 数据元素(Data Element)

    • 数据元素是数据的基本单位，在计算机程序中通常作为一个整体进行考虑和处理。但它还可以分割成若干个具有不同属性的项(字段)。数据元素一般由一个或多个数据项组成。

  • 数据项(Data ltem )

    • 数据项是具有独立意义的最小数据单位，是对数据元素属性的描述。

  • 数据类型(Data Type)

    • 数据类型是一-组性质相同的值的集合以及定义于这个值的集合，上的一组操作的总称。
    • 每个数据项属于某一确定的基本数据类型

  • 数据结构(Data Structure )

    • 指数据元素之间的关系，按照某种关系组织起来，以一定的方式存储，并在这些数据上定义了一个运算的集合。
    • 数据元素都不是孤立存在的，它们之间存在着某种关系，这种相互关系就称为结构，带有结构的数据对象称为数据结构。

1.2 数据的逻辑结构

1. 基本概述

image-20220219134303518

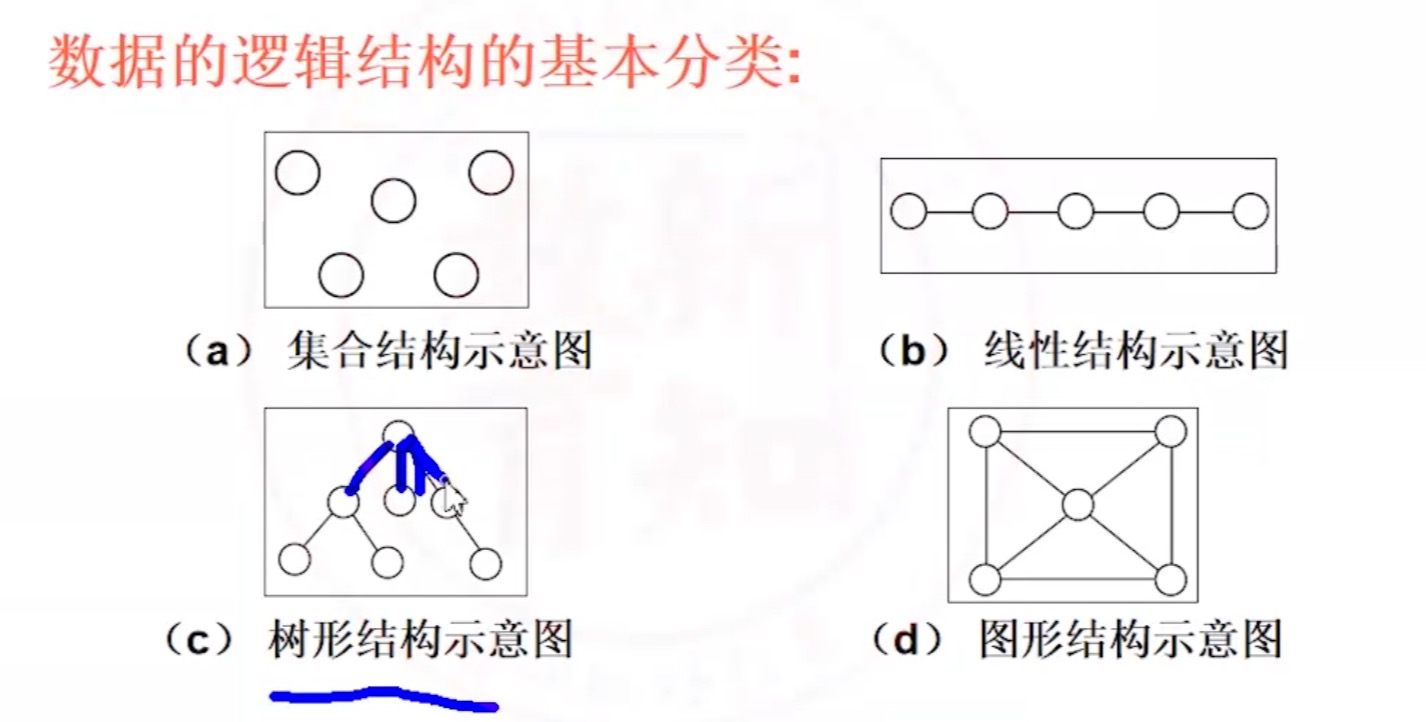
image-20220219134316924

2. 逻辑结构的数学定义方法

image-20220219134550944

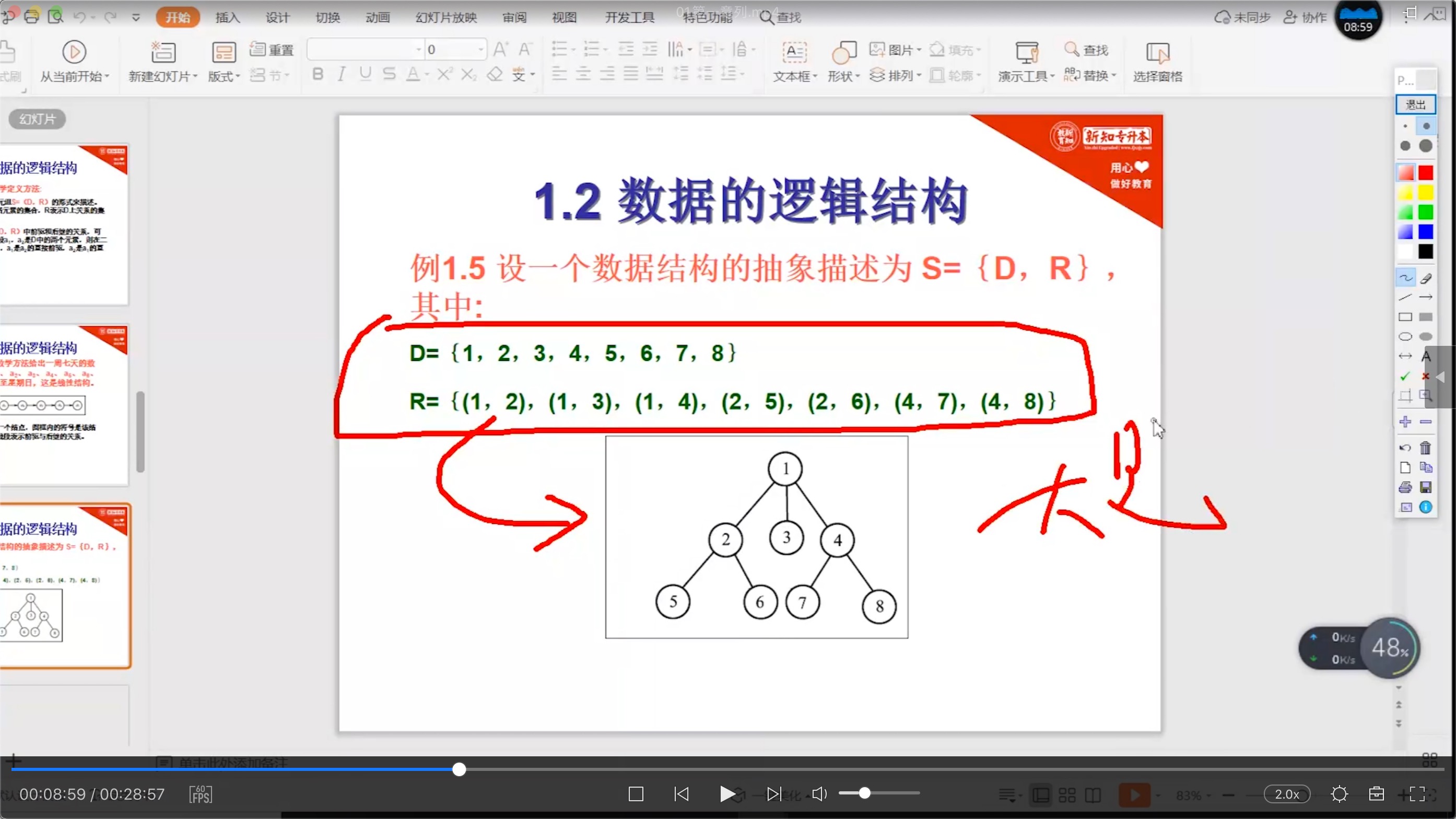
image-20220219134608928

1.3 算法的描述

1. 算法的简介

image-20220219134709663

2. 算法的性质

image-20220219134901018

3. 算法的设计要求

image-20220219134929615

4. 算法的评价

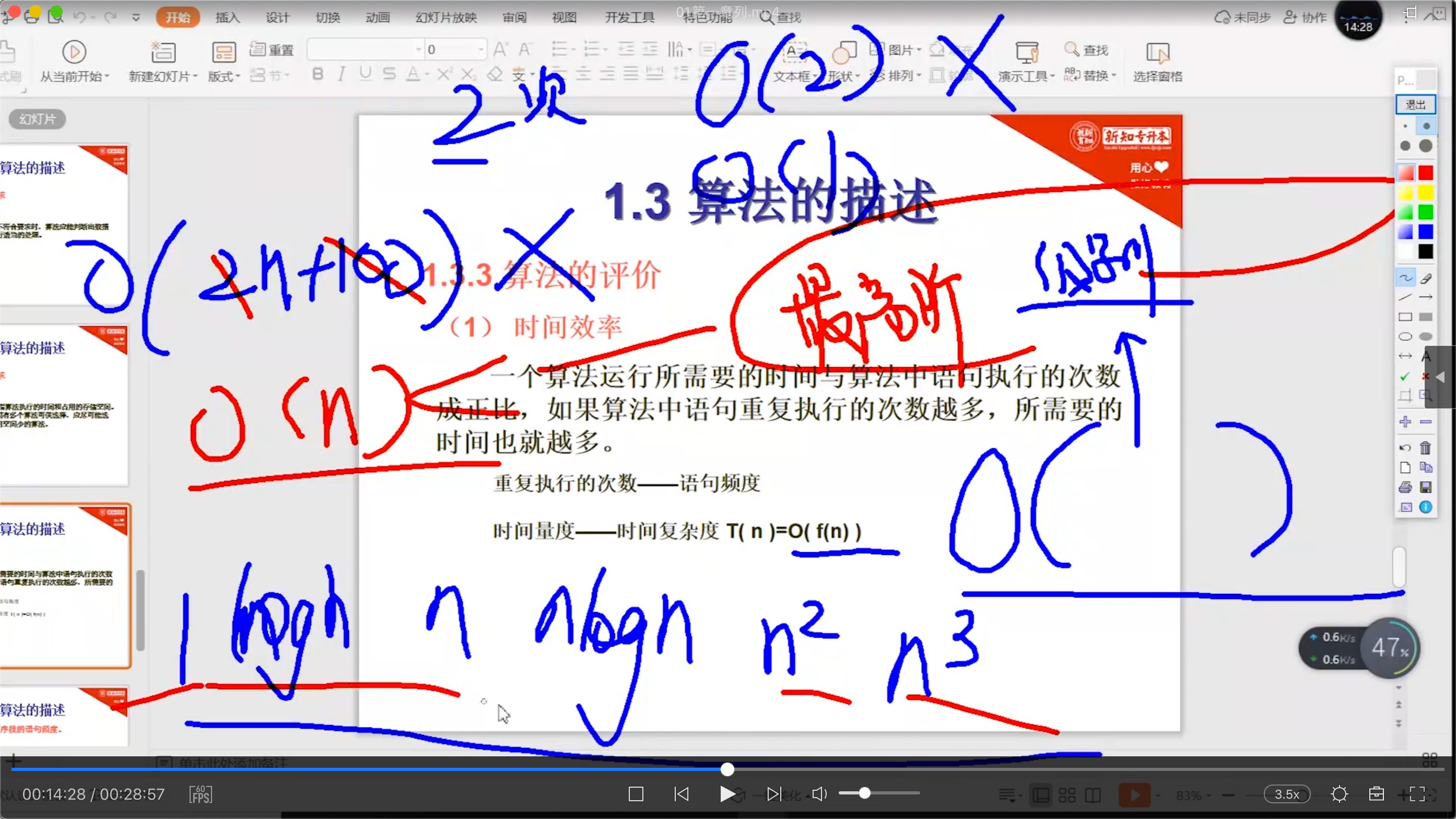
image-20220219135047741

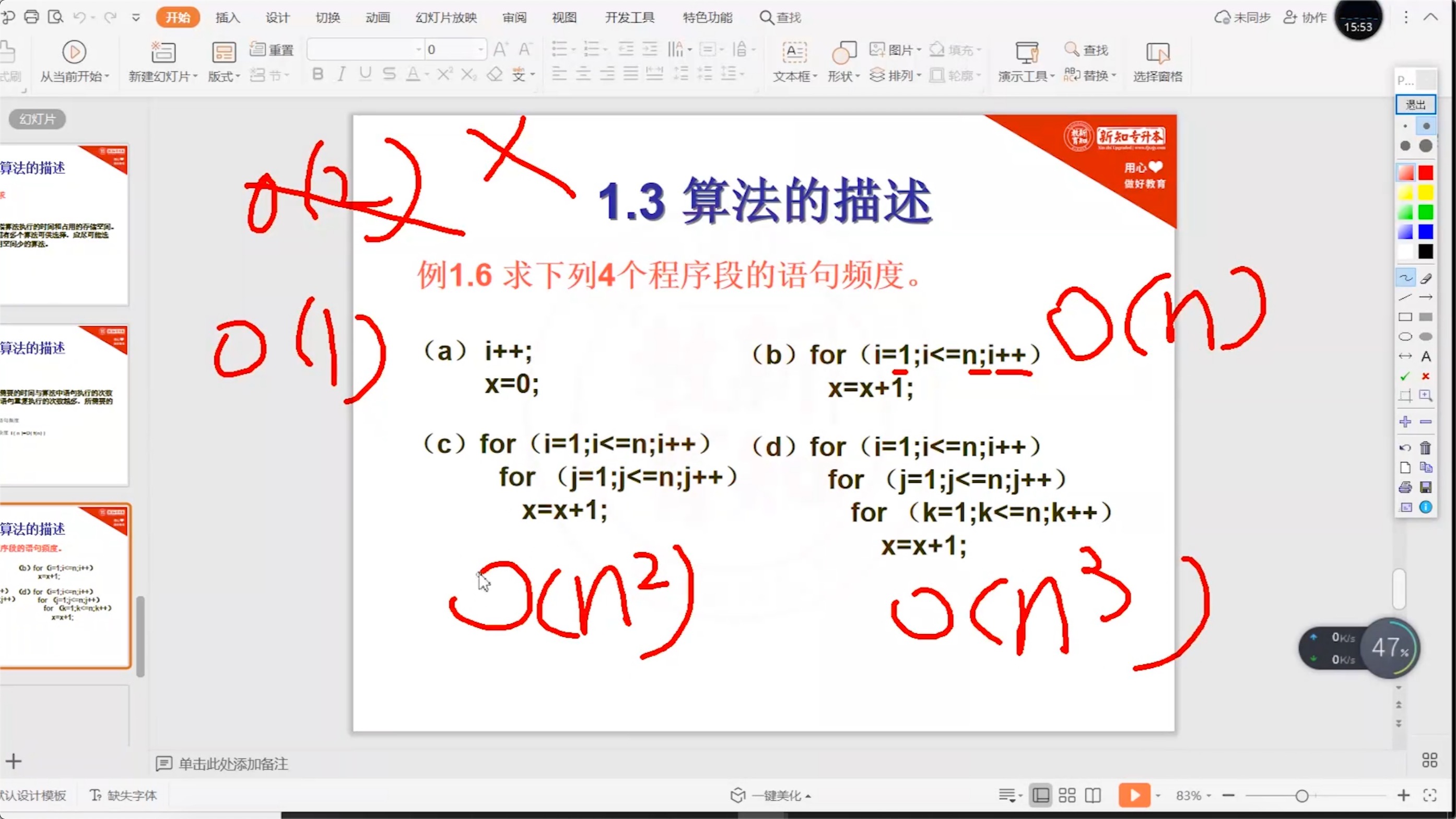
image-20220219135155185

image-20220219135359245

1.4 本章小结

image-20220219135438845

第 2 章 - 线性表

2.1 线性表_基本概述

2.1.1 线性表_定义

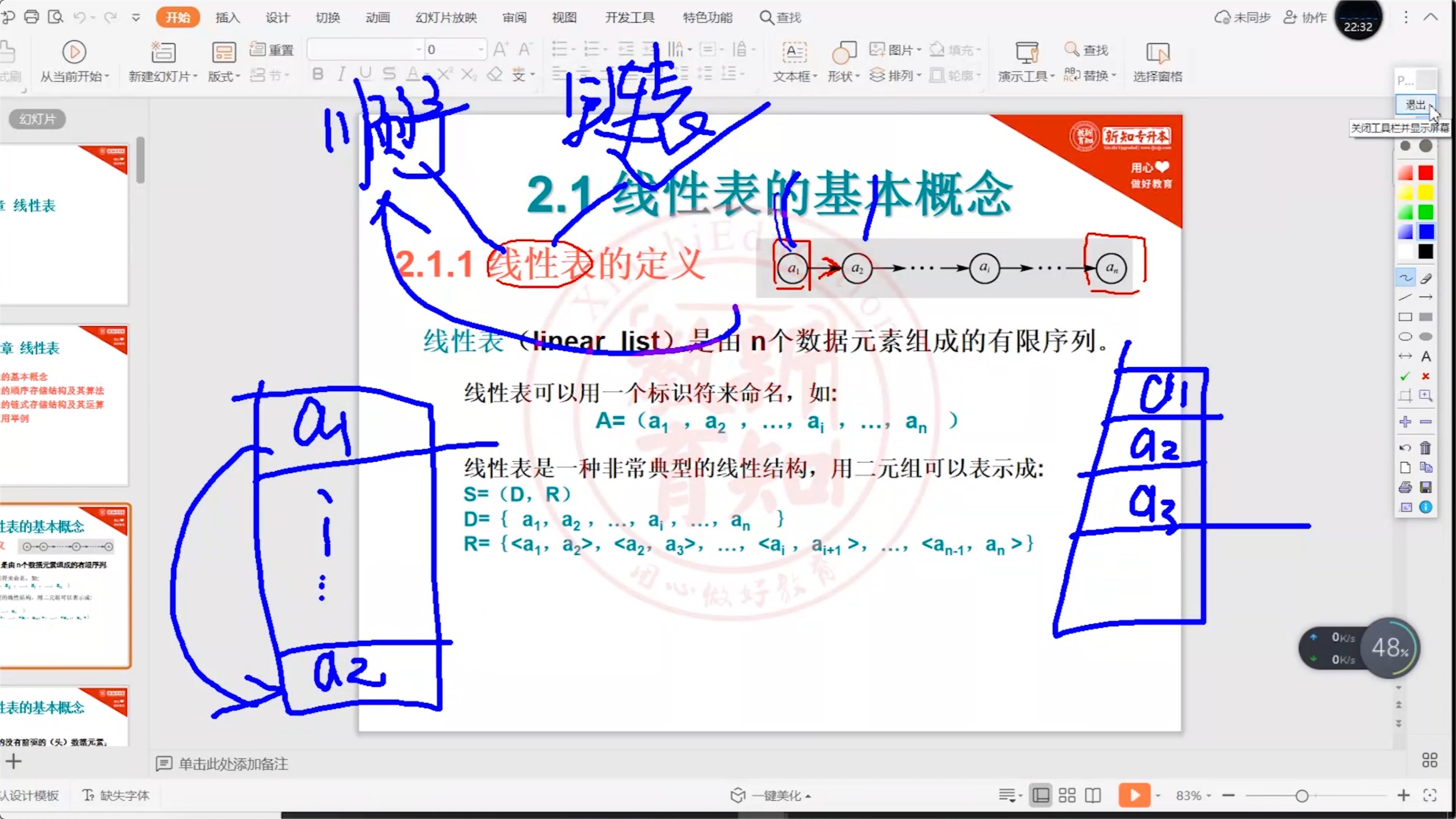
image-20220219135740568

2.1.2 线性表_特点

image-20220219135834183

2.2 线性表的顺序存储结构及其算法

2.2.1 顺序存储结构_概述

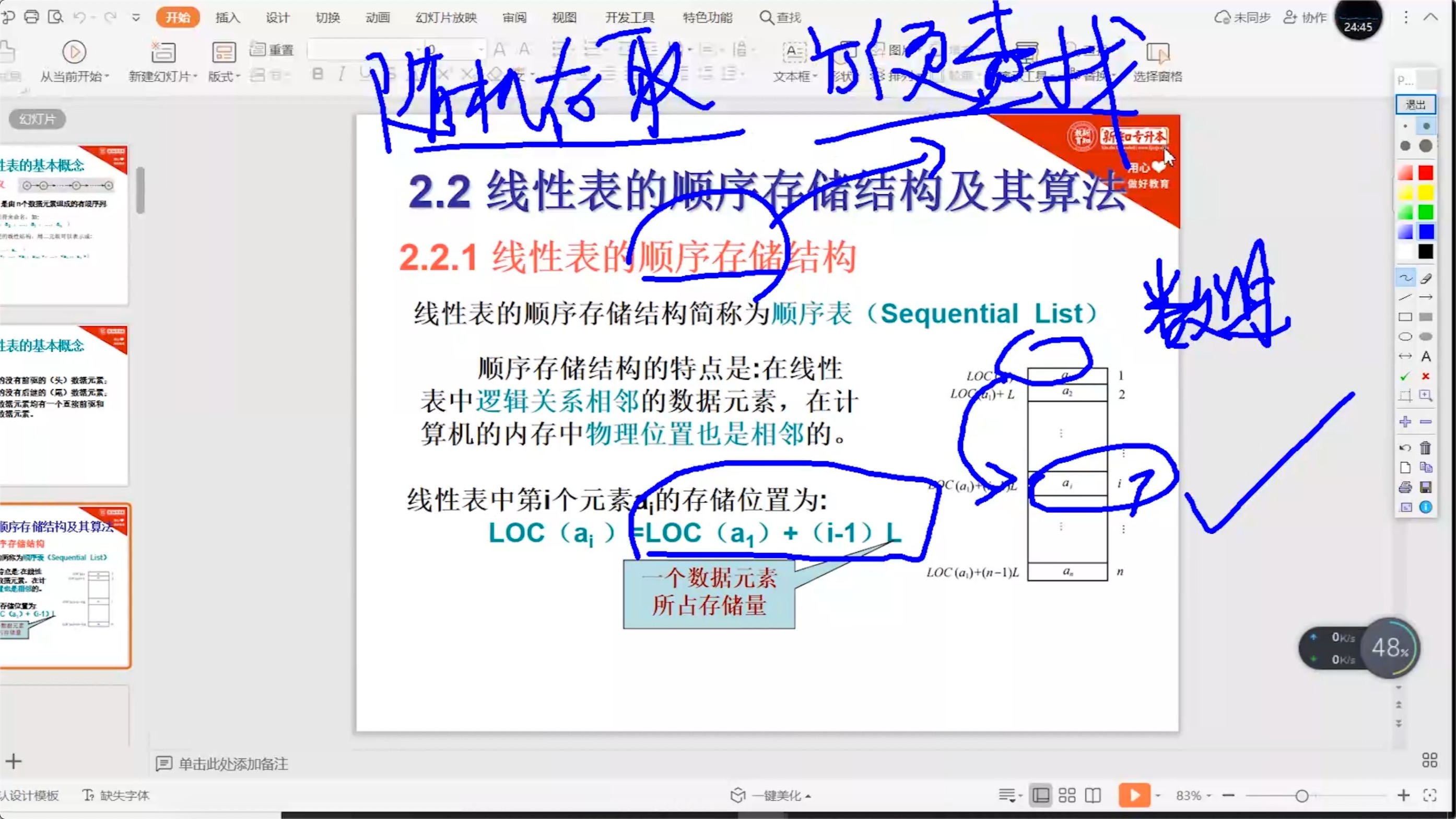
image-20220219140005445

2.2.2 顺序存储结构_定义

C语言版本

  • #include <stdio.h>

#define MAXLEN 100    // 顺序表最大元素个数
typedef int Elemtype; // 为int类型取别名 , Elemtype为元素数据类型的变量

typedef struct
{
    Elemtype List[MAXLEN]; // 定义线性表(数组)
    int length;            // 定义表长度
} SqList;                  // 定义新结构体类型

2.2.3 顺序表_插入运算

  • 定义顺序表结构

    #include <stdio.h>

#define MAXLEN 100    // 顺序表最大元素个数
typedef int Elemtype; // 为int类型取别名 , Elemtype为元素数据类型的变量

typedef struct
{
    Elemtype List[MAXLEN]; // 定义线性表(数组)
    int length;            // 定义表长度
} SqList;                  // 定义新结构体类型

  • 插入操作代码

    // 顺序表_插入操作
int insertsqlist(int i, Elemtype x, SqList *sql)
{
    // 在顺序表(*sql)的第i个元素之前插入一个新元素x
    int j;
    if ((i < 1) || (i > sql->length)) // i值非法，返回值为0
    {
        return 0;
    }
    else
    {
        for (j = sql->length; j >= i; j--)
            sql->List[j + 1] = sql->List[j]; // 向后移动数据，腾出要插入的空位
        sql->List[j + 1] = x;                // 修正插入位置为j+1
        (sql->length)++;                     // 表长+1
        return 1;                            // 插入成功返回值为1
    }
}

  • 图文并茂讲解

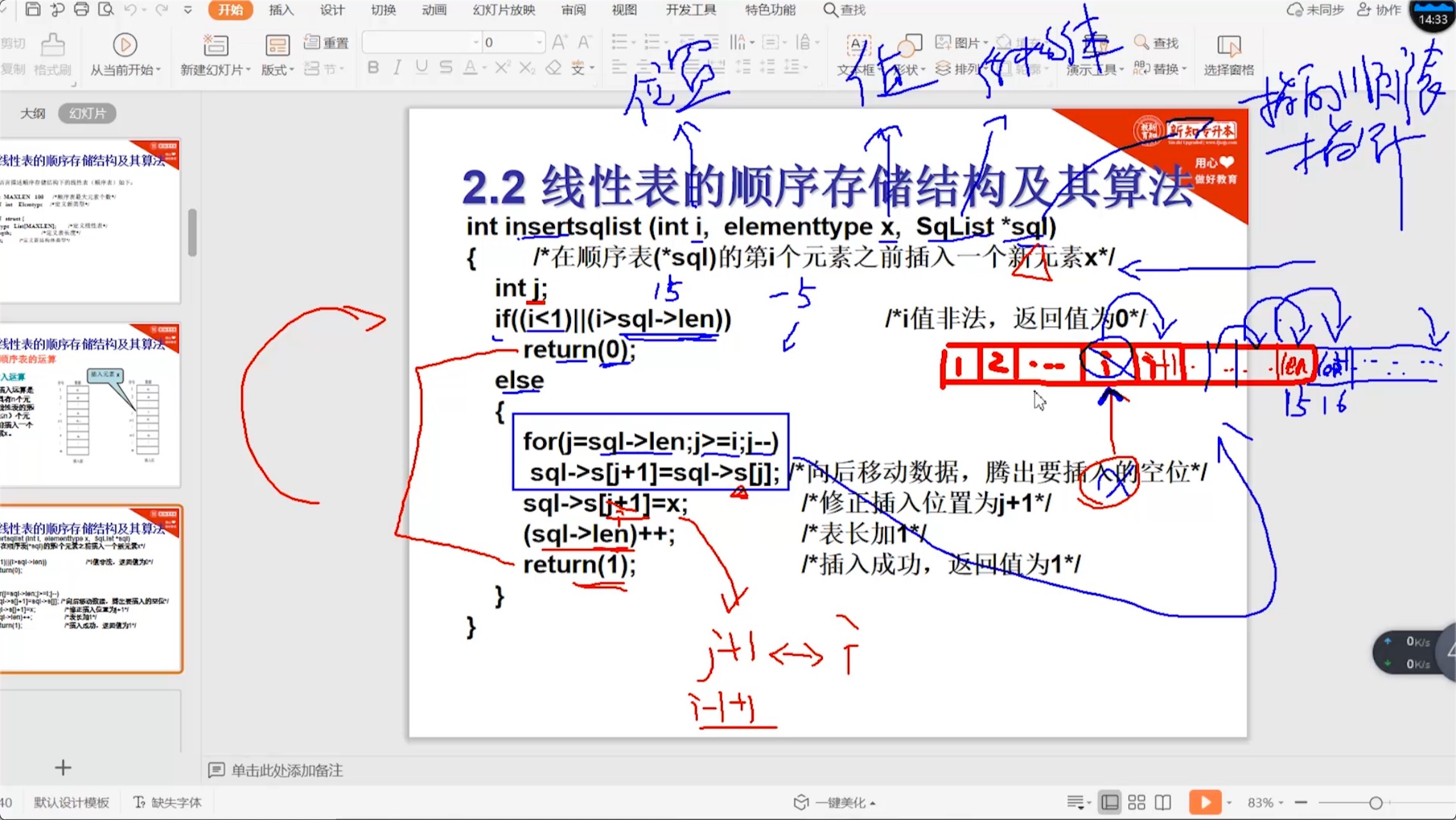
    image-20220219142219852

  • 顺序表的插入效率贼低

    image-20220219142303578

2.2.4 顺序表_删除运算

  • 定义顺序表结构

    #include <stdio.h>

#define MAXLEN 100    // 顺序表最大元素个数
typedef int Elemtype; // 为int类型取别名 , Elemtype为元素数据类型的变量

typedef struct
{
    Elemtype List[MAXLEN]; // 定义线性表(数组)
    int length;            // 定义表长度
} SqList;                  // 定义新结构体类型

  • 顺序表_删除操作

    // 顺序表_删除操作
int delsqlist(int i, SqList *sql)
{ // 删除顺序表(*sql)的第i个元素
    int j;
    if ((i < 1) || (i > sql->length)) // i值非法，返回值为0
    {
        return 0;
    }

    else
    {
        for (j = i + 1; j <= sql->length; j++)
            sql->List[j - 1] = sql->List[j]; // 向前移动数据，覆盖前一个数据
        (sql->length)--;                     // 表长度减1
        return 1;                            // 删除成功，返回值为1
    }
}

  • 图文并茂

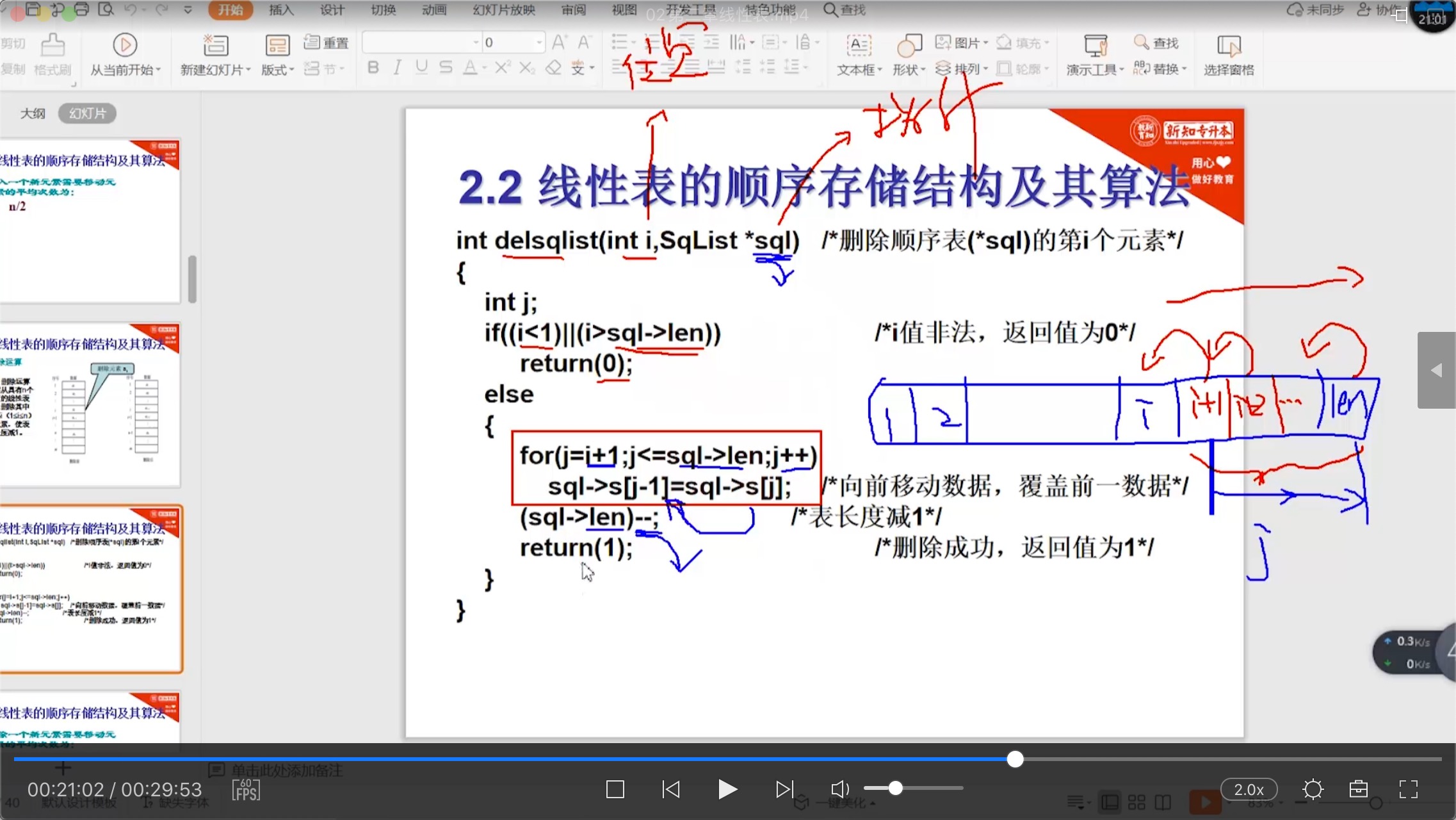
    image-20220219143404329

  • 顺序表的删除元素效率也是蛮低的

    image-20220219143449995

2.3 线性表的链式存储结构及其运算

2.3.1 链式存储结构_概述

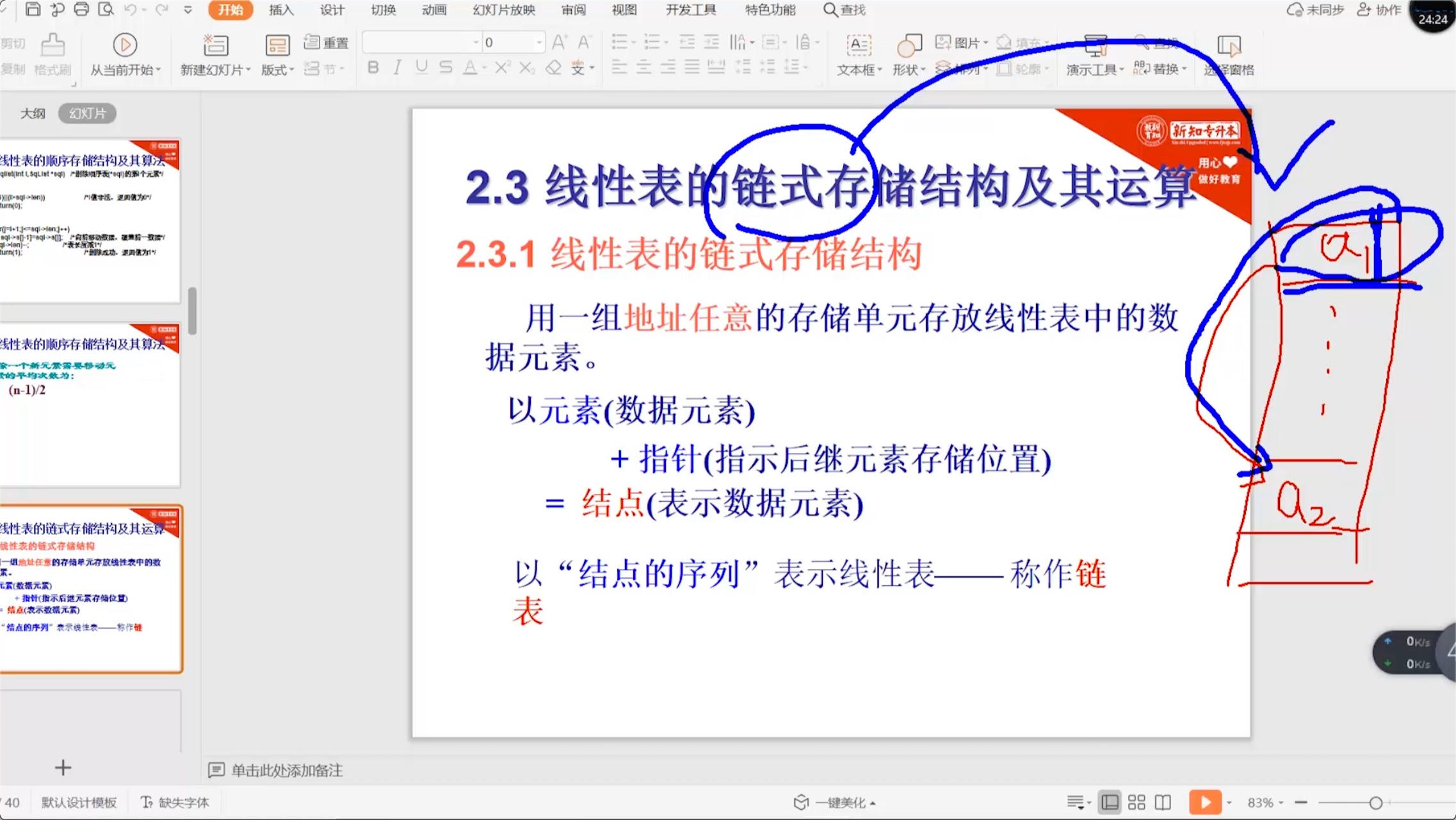
image-20220219143659787

2.3.2 链式存储结构_定义

C语言版本

  • #include <stdio.h>

// 该结构体用于保存一个节点的信息
typedef struct node
{
    int data;  // 当前地址值
    struct node *next;  // 下个元素的地址值
} NODE;

2.3.3 链式存储结构_图介绍

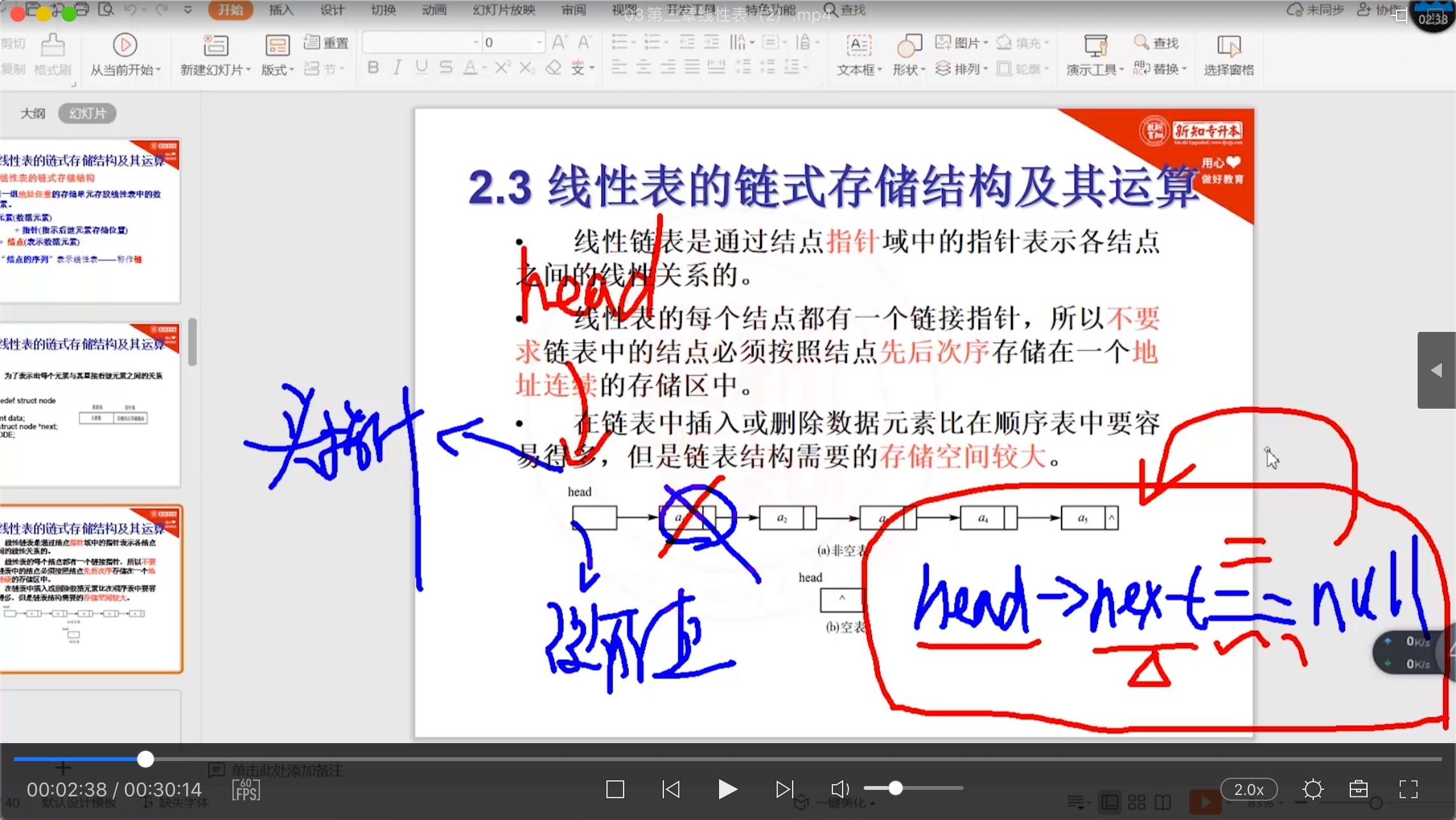
image-20220219144650484

2.3.4 单链表的创建(了解)

C语言版本

#include <stdio.h>
#include <stdlib.h>

// 该结构体用于保存一个节点的信息
typedef struct node
{
    int data;          // 当前地址值
    struct node *next; // 下个元素的地址值
} NODE;

// 创建单链表
NODE *create() // 此函数采用后插入方式建立单链表
{
    NODE *head, *q, *p; // 定义指针变量
    char ch;
    int a;
    head = (NODE *)malloc(sizeof(NODE)); // 申请新的存储控件，建立表头节点

    q = head;
    ch = '*';
    printf("\nInput the list:");

    while (ch != '?') // ch为是否建立新结点的标识，若 ch为 ？则输入结束
    {
        scanf("%d", &a); // 输入新元素
        p = malloc(sizeof(NODE));
        p->data = a;
        q->next = p;
        q = p;
        ch = getchar(); // 读入输入与否的标志
    }
    q->next = NULL;
    return head; // 返回表头指针head
}

2.3.5 单链表_查找

1. 按序号查找
#include <stdio.h>
#include <stdlib.h>

// 该结构体用于保存一个节点的信息
typedef struct node
{
    int data;          // 当前地址值
    struct node *next; // 下个元素的地址值
} NODE;

// 单链表查找（按序号查找）
NODE *find(NODE *head, int i)   // 在已知链表中查找给定的序号：i
{
    int j = 1;
    NODE *p;
    p = head->next;
    while ((p != NULL) && (j < i)) // 核心判断条件，给👴🏻记住
    {
        p = p->next; // 指向下一个元素
        j++;
    }
    return p;
}

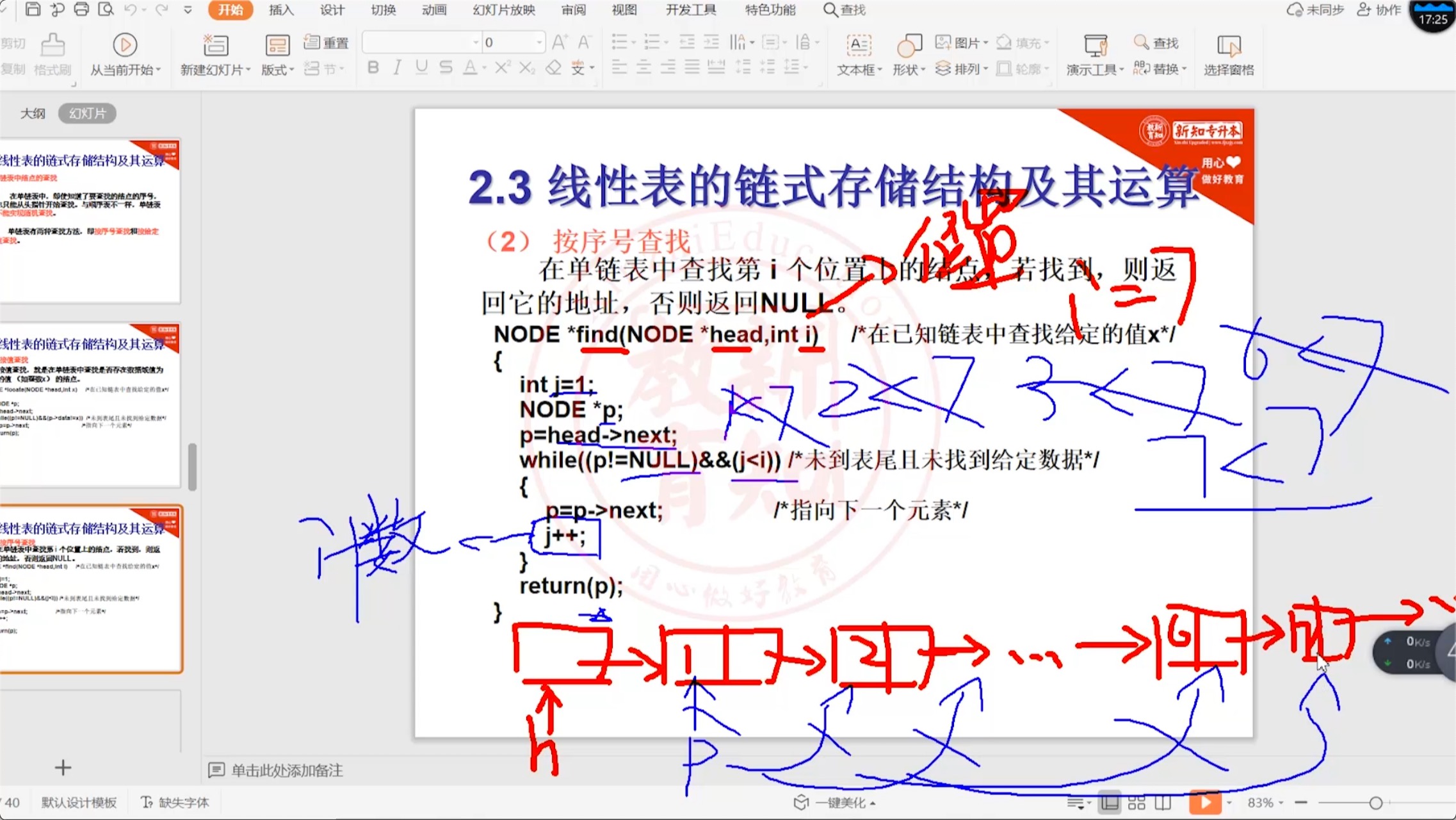
image-20220219151443106

2. 按给定值查找
#include <stdio.h>
#include <stdlib.h>

// 该结构体用于保存一个节点的信息
typedef struct node
{
    int data;          // 当前地址值
    struct node *next; // 下个元素的地址值
} NODE;

// 单链表查找（按值查找）
NODE *locate(NODE *head, int x)   // 在已知链表中查找给定的值：x
{
    NODE *p;
    p = head->next;
    while ((p != NULL) && (p->data != x)) // 未到表尾且未找到给定数据
    {
        p = p->next; // 指向下一个元素
    }
    return p;
}

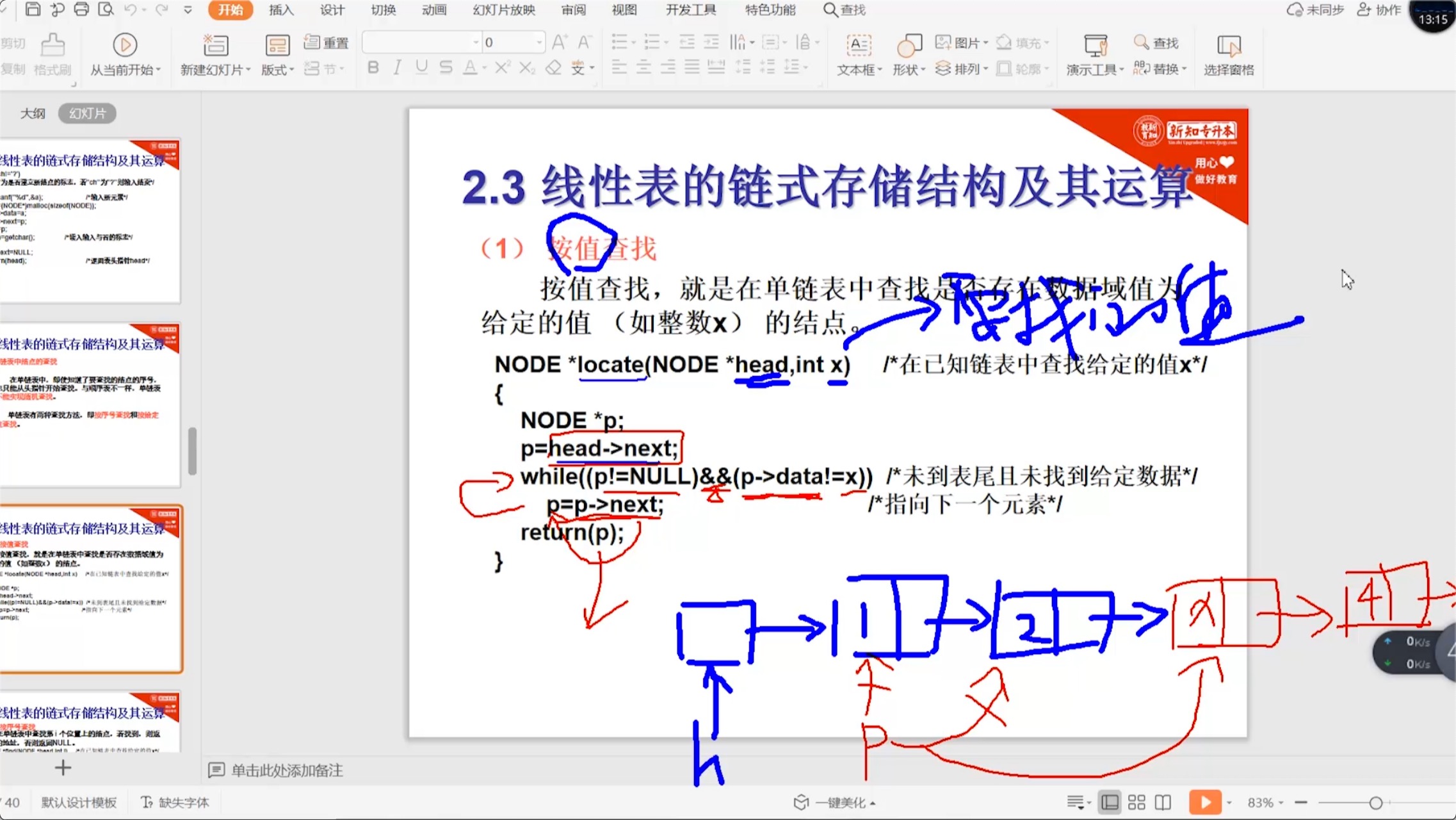
image-20220219150826534

2.3.6 单链表_插入

image-20220219151647709

#include <stdio.h>
#include <stdlib.h>

// 该结构体用于保存一个节点的信息
typedef struct node
{
    int data;          // 当前地址值
    struct node *next; // 下个元素的地址值
} NODE;

// 单链表_插入
void insert(NODE *p, int x) // 在链表的p节点后插入给定元素x
{
    NODE *q;
    q = malloc(sizeof(NODE)); // 申请新的存储空间
    q->data = x;
    q->next = p->next; // 实现图的①
    p->next = q;       // 实现图的②
}

2.3.7 单链表_删除

image-20220219152432348

#include <stdio.h>
#include <stdlib.h>

// 该结构体用于保存一个节点的信息
typedef struct node
{
    int data;          // 当前地址值
    struct node *next; // 下个元素的地址值
} NODE;

// 单链表_删除
void delete (NODE *head, int x) // 删除链表中的给定元素x
{
    NODE *p, *q;
    q = head;
    p = q->next;

    while ((p != NULL) && (p->data != x)) // 查找要删除的元素
    {
        q = p;
        p = p->next;
    }
    if (p == NULL)
    {
        printf("%d not found.\n", x); // x结点未找到
    }
    else
    {
        q->next = p->next; // 链接x直接后继节点
        free(p);           // 删除x结点，释放x结点空间
    }
}

2.4 循环链表结构(了解)

2.4.1 循环链表结构_概述

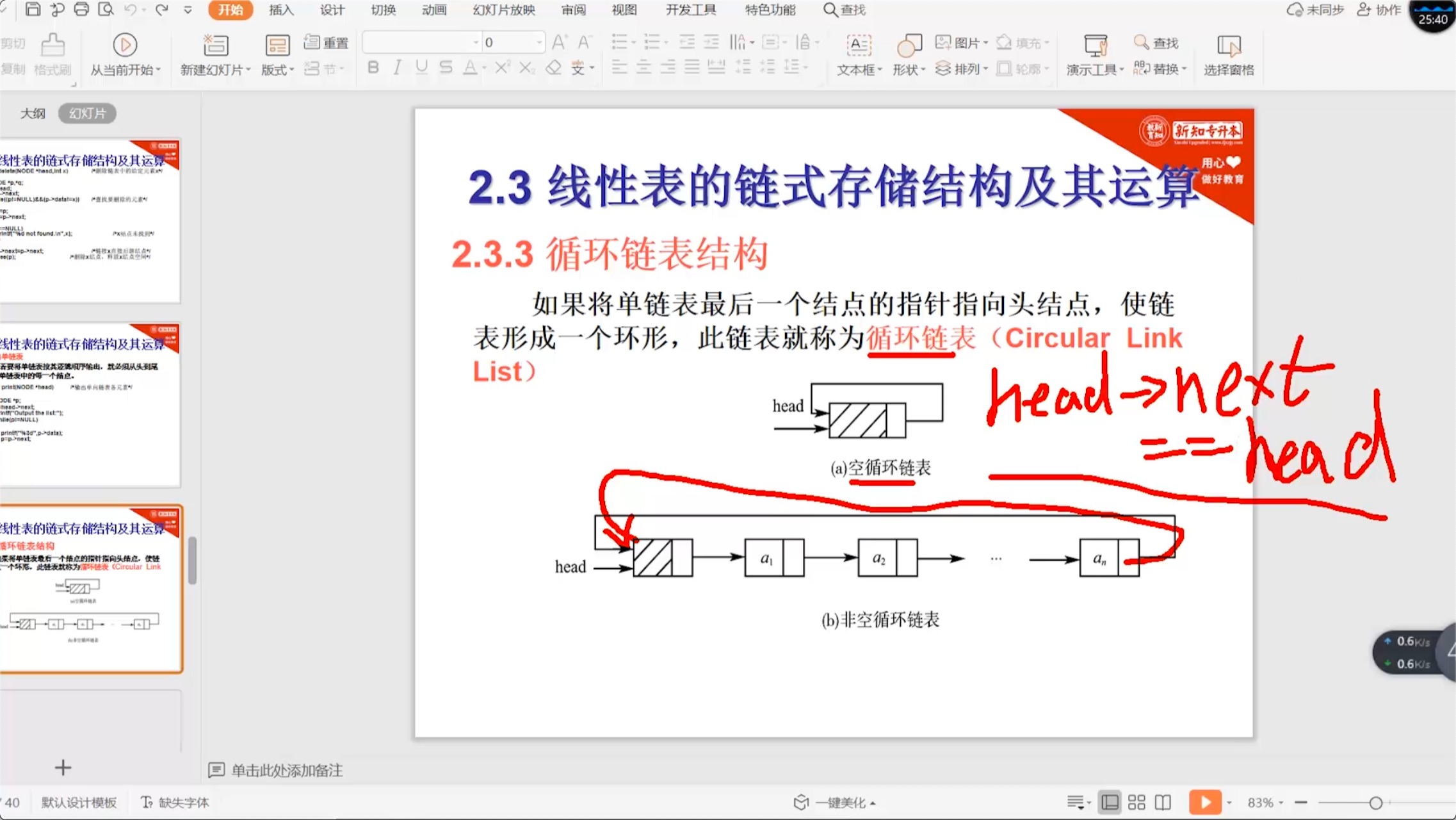
image-20220219153629262

2.5 双向链表结构

2.5.1 双向链表_概述

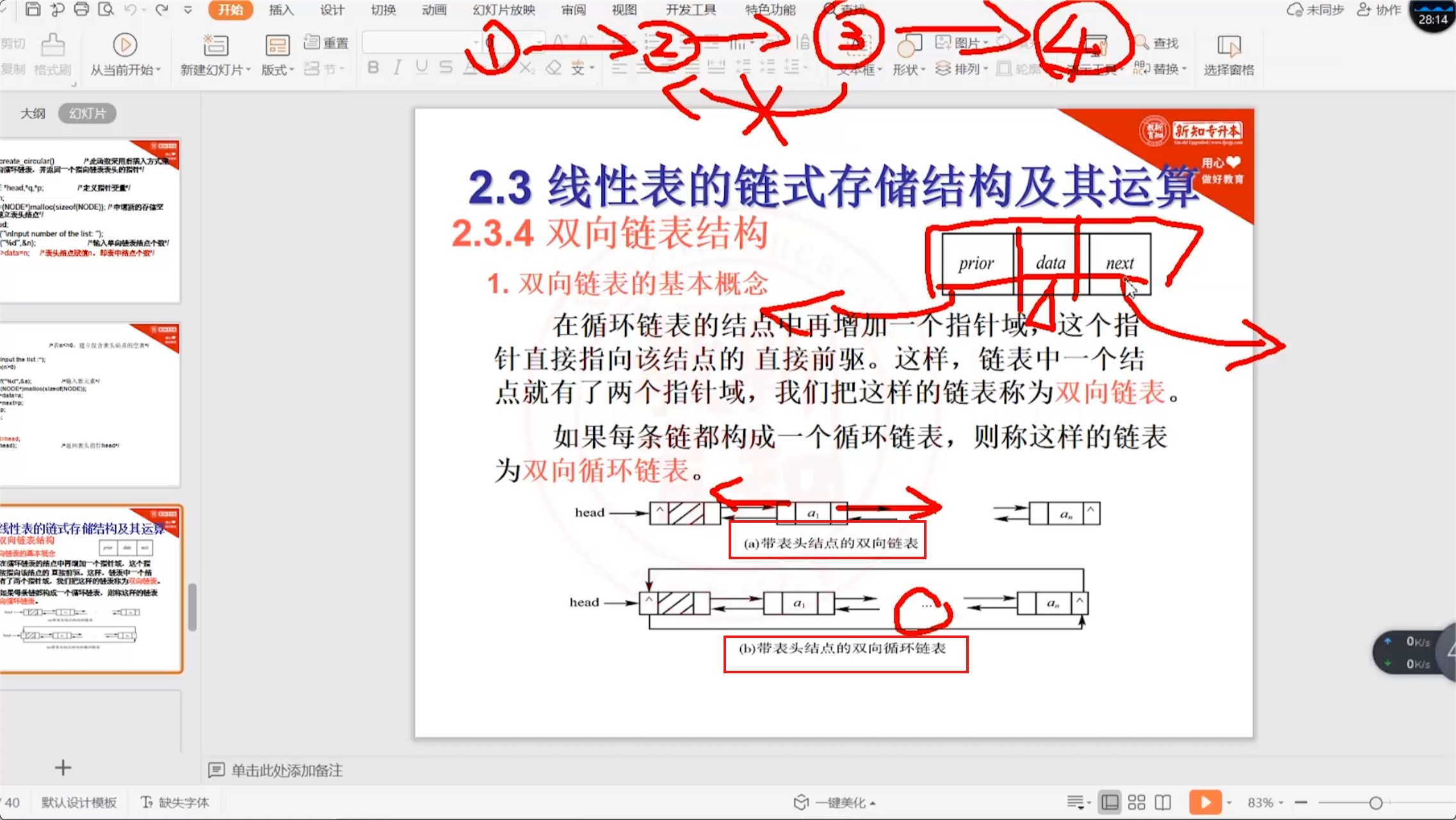
image-20220219153933021

2.5.2 双向链表_插入

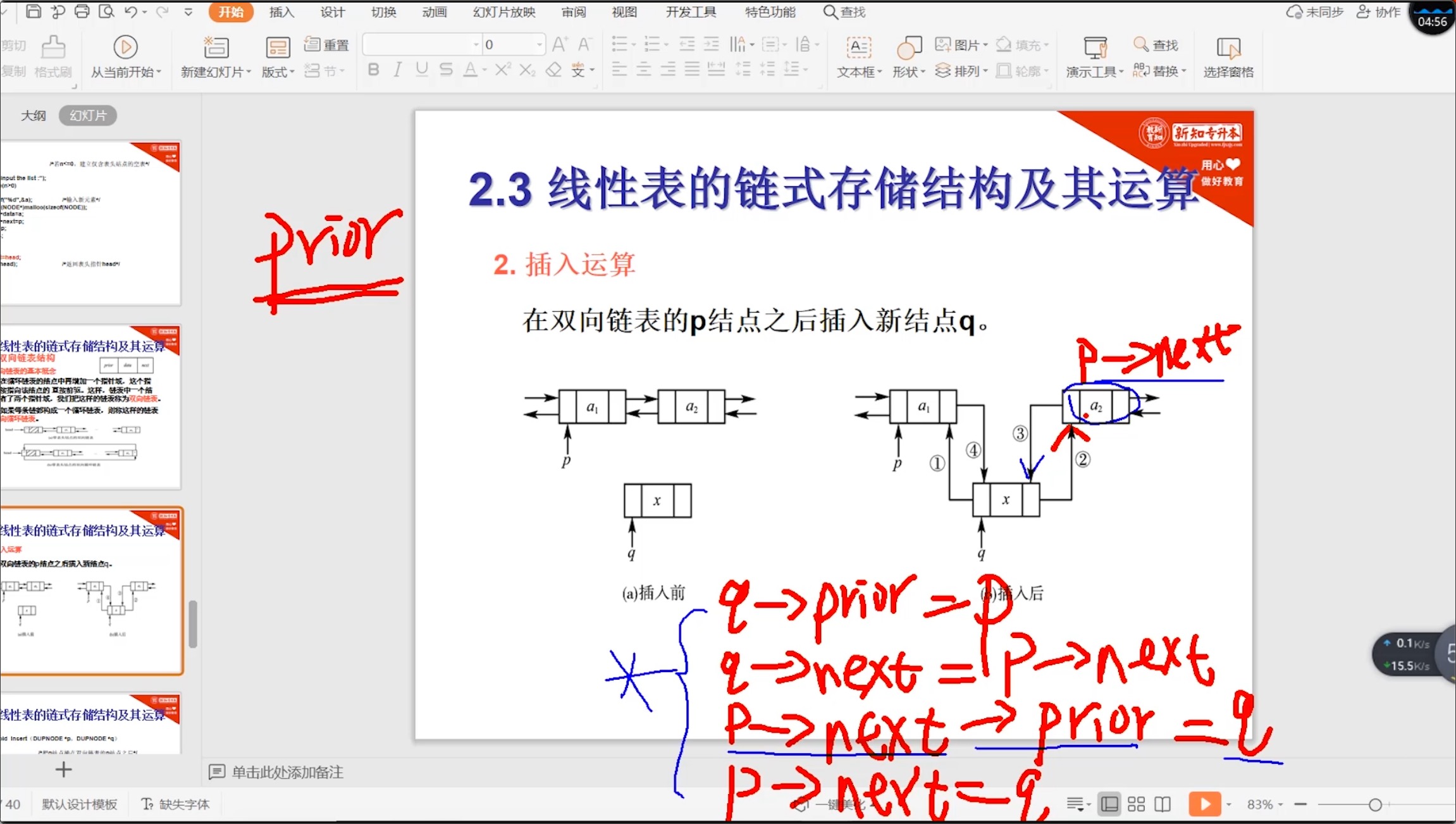
!image-20220219193843252

void insert(DUPNODE *p, DUPNODE *q) {
    // 把q结点插在双向链表的p结点之后
    q->prior = p;
    q->next = p->next;
    p->next->proir = q;
    p->next = q;
}

2.5.3 双向链表_删除

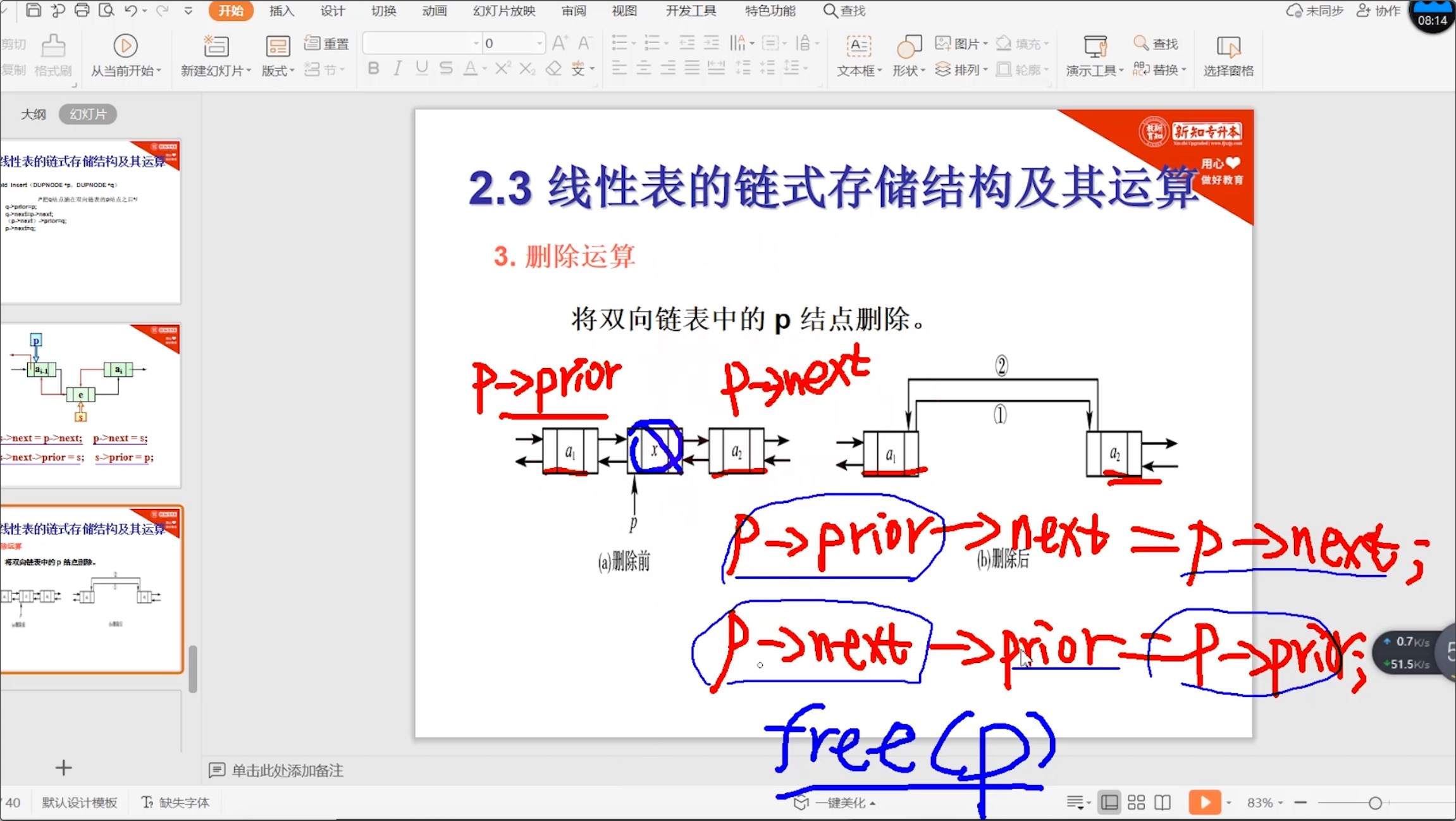
image-20220219194347161

void delete(DUPNODE *p) {
    // 在双向链表中删除结点p
    p->prior->next = p->next;
    p->next->prior = p->proir;
    free(p);
}

第 3 章 - 栈与队列

3.1 栈_顺序存储

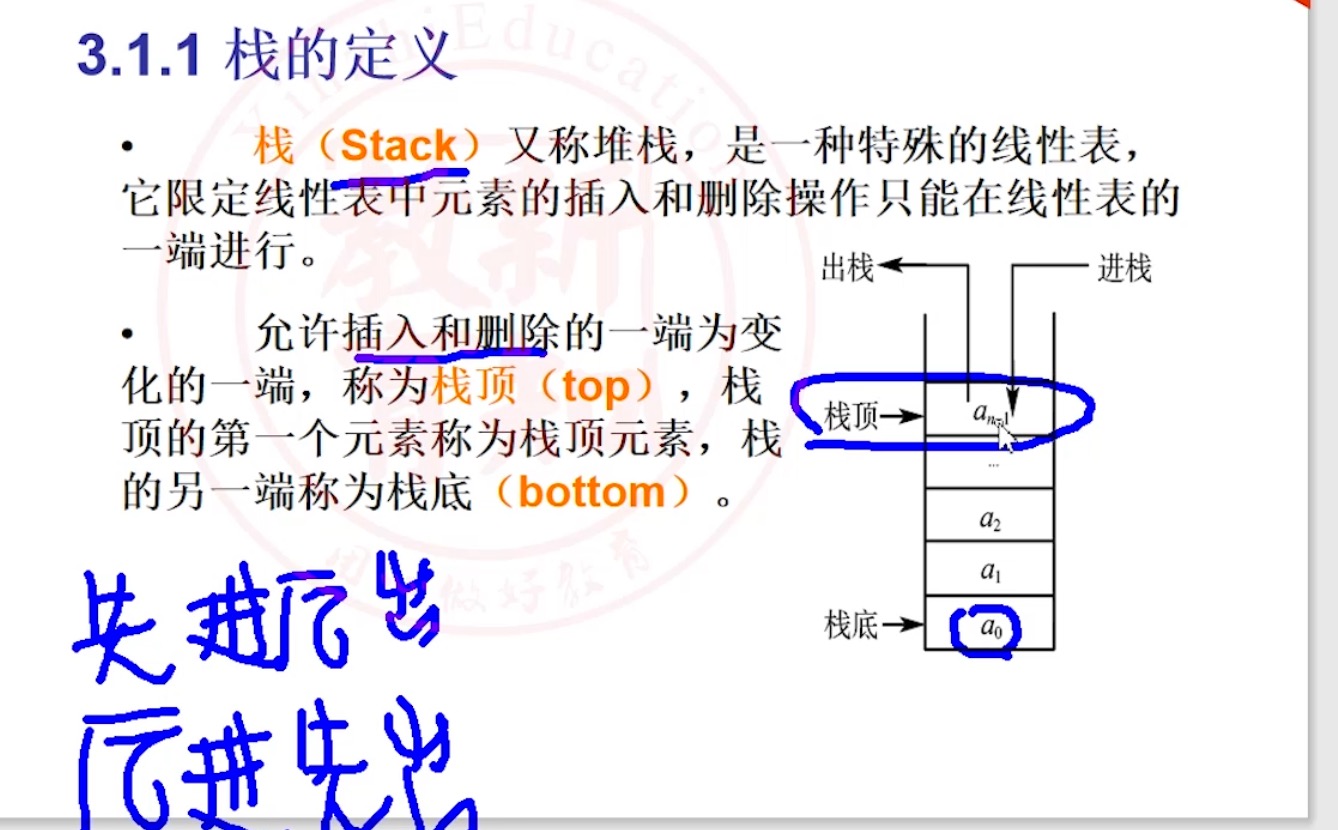
3.1.1 栈_相关概念

image-20220219195213429

image-20220219195227498

3.1.2 顺序存储栈_定义(代码)

  • 栈的定义

    #include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 定义栈结构体类型
typedef struct
{
    elementType data[MAXLEN]; // 存放栈元素的数组
    int top;                  // 栈顶指针
} SqStack;

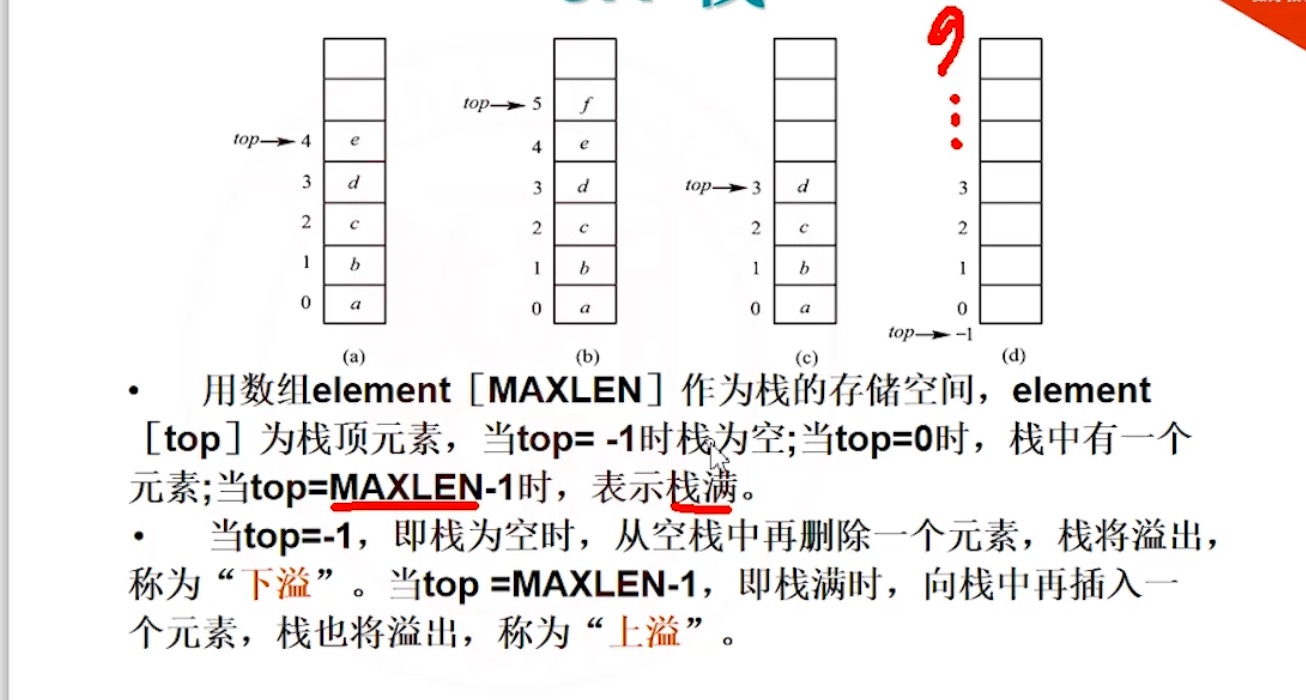
image-20220219195755724

3.1.3 初始化顺序栈

#include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 定义栈结构体类型
typedef struct
{
    elementType data[MAXLEN]; // 存放栈元素的数组
    int top;                  // 栈顶指针
} SqStack;

// 建立一个空栈
SqStack initStack_sq()
{
    SqStack s;
    s.top = -1;
    return s;
}

3.1.4 取栈顶元素

#include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 定义栈结构体类型
typedef struct
{
    elementType data[MAXLEN]; // 存放栈元素的数组
    int top;                  // 栈顶指针
} SqStack;

// 取栈顶元素，若栈s非空，用 *x 返回栈顶元素
int getTop_sq(SqStack *s, elementType *x)
{
    if (s->top == -1)
    {
        return 0; // 空栈返回0
    }
    else
    {
        *x = s->data[s->top];
        return 1;
    }
}

3.1.5 进栈操作

#include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 定义栈结构体类型
typedef struct
{
    elementType data[MAXLEN]; // 存放栈元素的数组
    int top;                  // 栈顶指针
} SqStack;

// 进栈操作，若栈s未满，则将元素x进栈
int Push_sq(SqStack *s, elementType x)
{
    if (s->top == MAXLEN - 1) {
        return 0;    // 栈满返回0   
    }
    s->top++;
    s->data[s->top] = x;
    return 1;
}

3.1.6 出栈操作

#include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 定义栈结构体类型
typedef struct
{
    elementType data[MAXLEN]; // 存放栈元素的数组
    int top;                  // 栈顶指针
} SqStack;

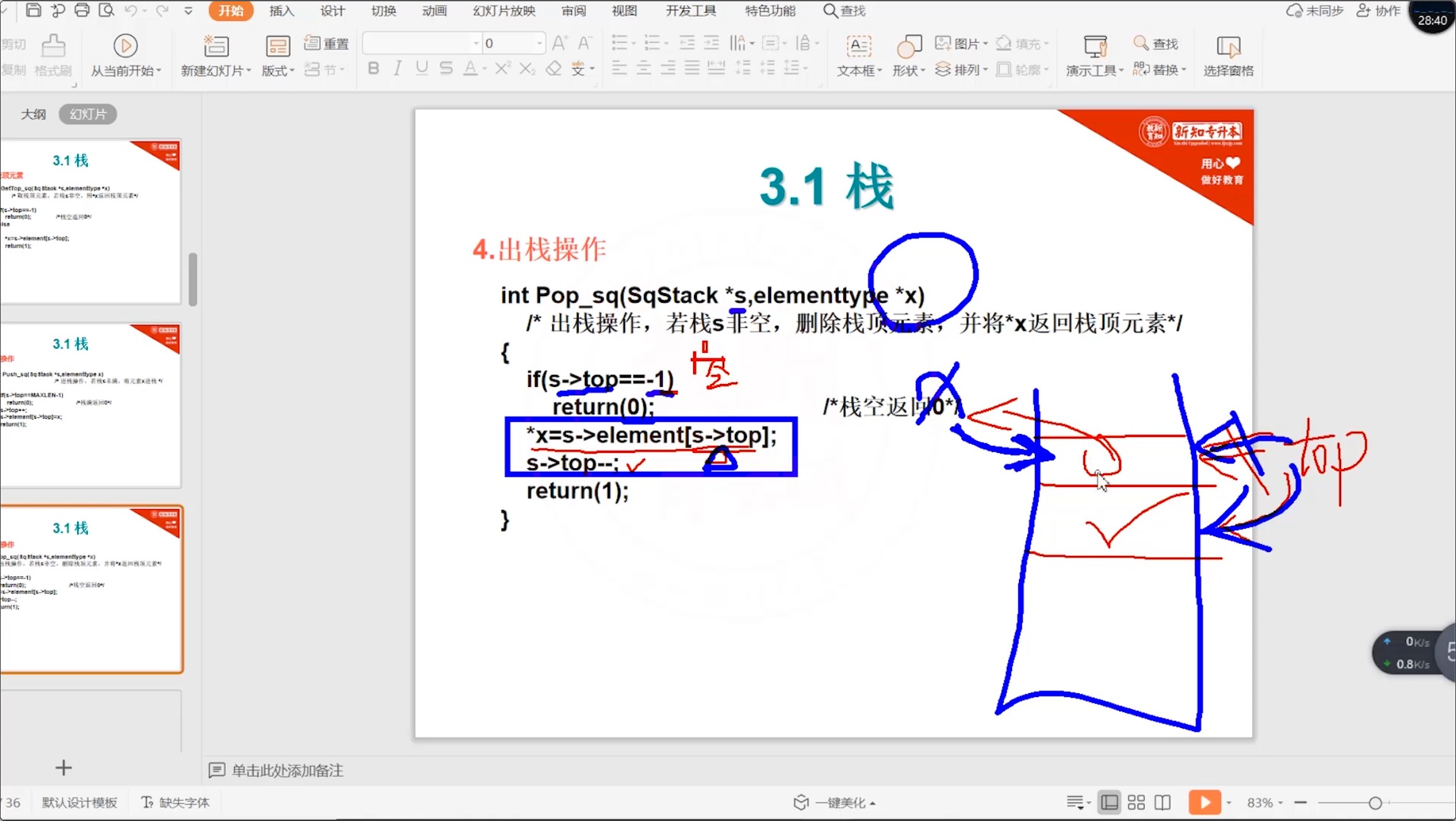
// 出栈操作，若栈s非空，删除栈顶元素，并将 *x 返回栈顶元素
int Pop_sq(SqStack *s, elementType *x)
{
    if (s->top == -1) {
        return 0;    // 栈空返回0   
    }
    *x = s->data[s->top];
    s->top--;
    return 1;
}

image-20220219201321603

3.1.7 判断空栈操作

#include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 定义栈结构体类型
typedef struct
{
    elementType data[MAXLEN]; // 存放栈元素的数组
    int top;                  // 栈顶指针
} SqStack;

// 判断空栈操作
int Empty_sq(SqStack *s) {
    return s->top == -1;
}

3.2 栈_链式存储

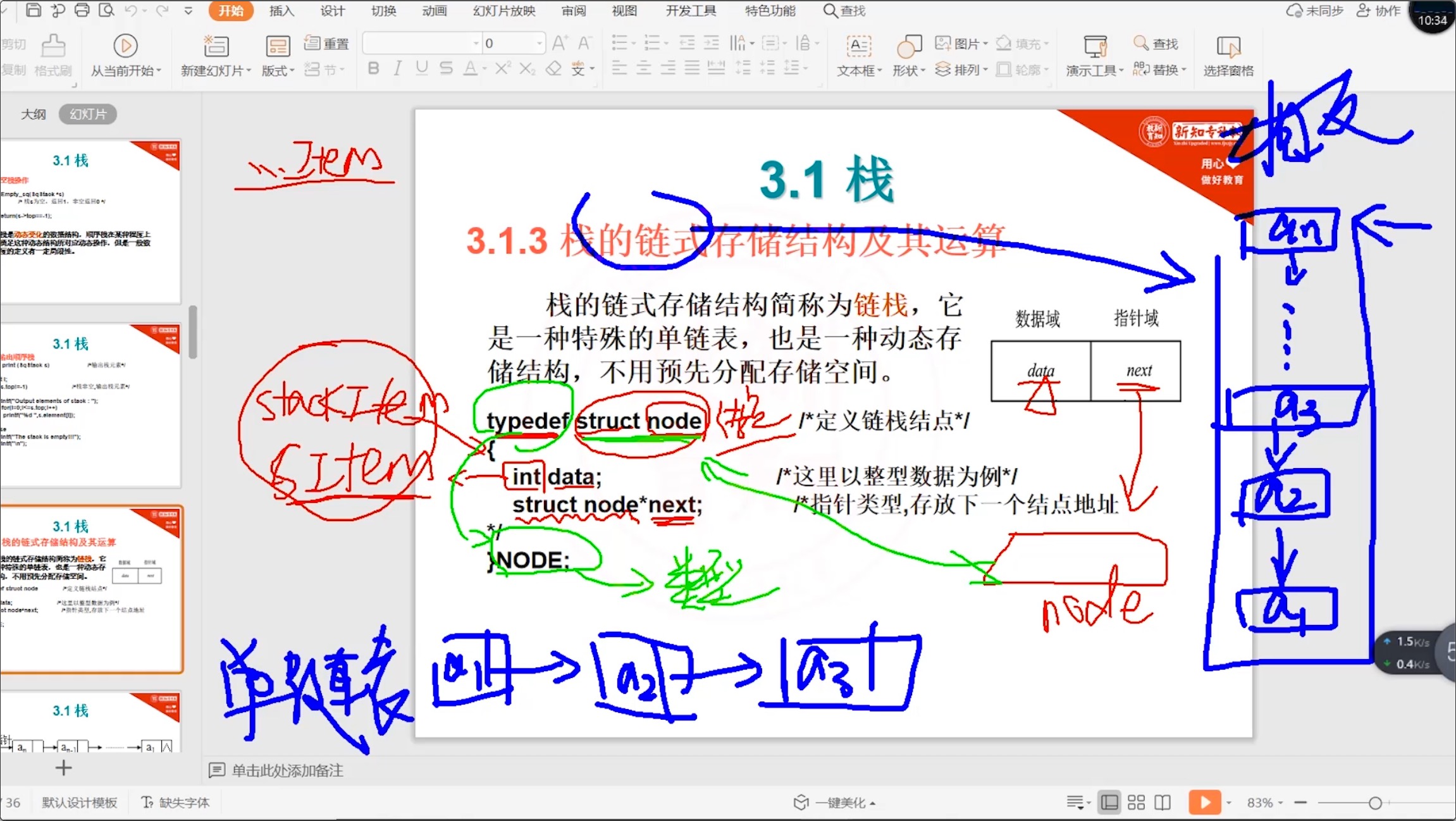
3.2.1 基本概述和链式存储栈_定义

image-20220219202342091

  • 链式存储栈的基本定义

    #include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 定义链栈结点
typedef struct node
{
    int data;         // 当前结点的地址值
    struct node *next // 下一个结点地址值
} NODE;

3.2.2 链式存储栈_进栈

  • C语言版代码实现

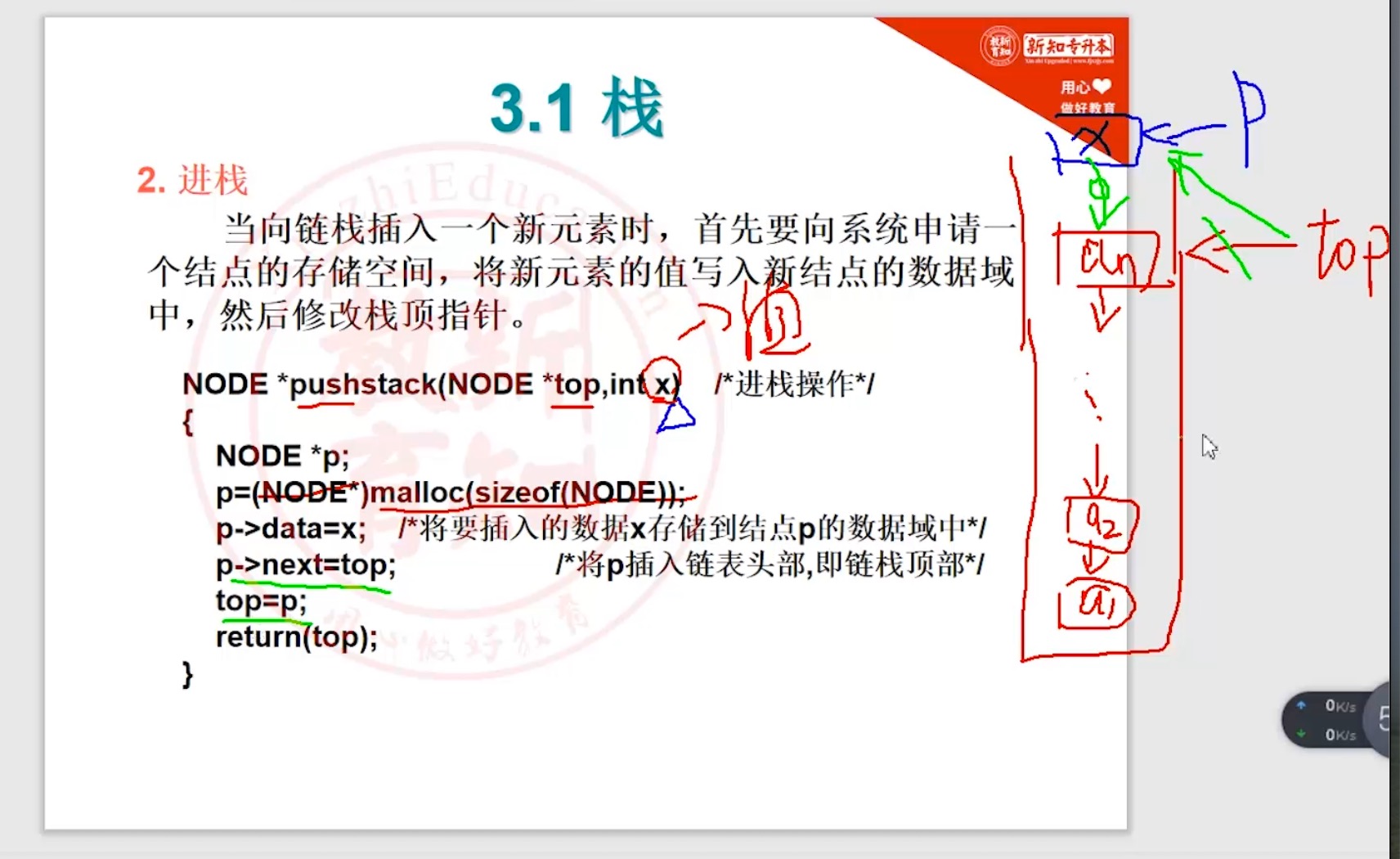
    #include <stdio.h>
#include <stdlib.h>
#define MAXLEN 10
typedef int elementType;

// 定义链栈结点
typedef struct node
{
    int data;         // 当前结点的地址值
    struct node *next // 下一个结点地址值
} NODE;

// 进栈操作
NODE *pushstack(NODE *top, int x)
{
    NODE *p;
    p = malloc(sizeof(NODE));
    p->data = x;   // 将要插入的数据x存储到结点p的数据域中
    p->next = top; // 将p插入链表头部，即链栈顶部
    top = p;
    return top;
}

  • 图文并茂

    image-20220219203920496

3.2.3 链式存储栈_出栈

  • C语言版代码

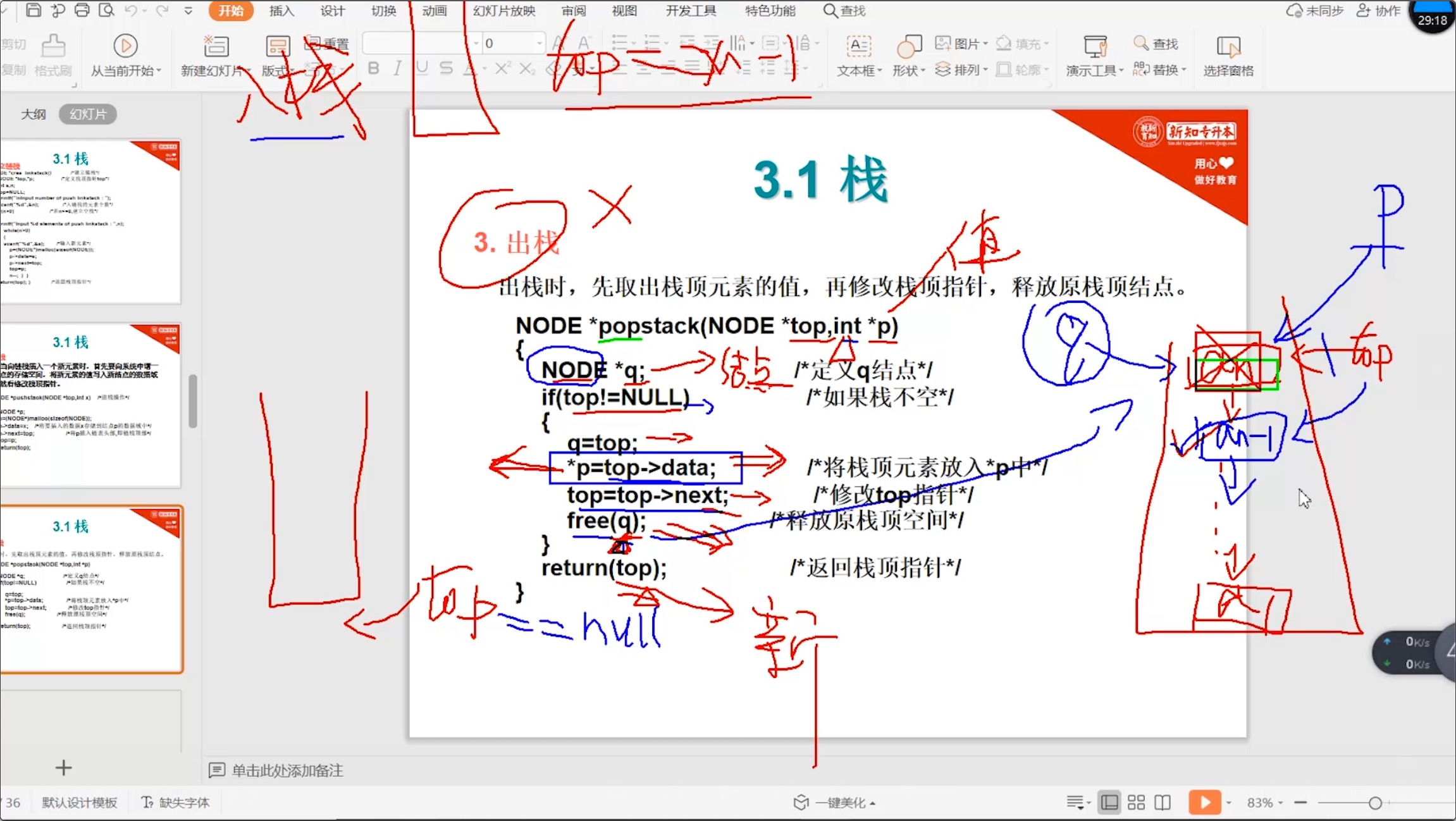
    #include <stdio.h>
#include <stdlib.h>

#define MAXLEN 10
typedef int elementType;

// 定义链栈结点
typedef struct node
{
    int data;         // 当前结点的地址值
    struct node *next // 下一个结点地址值
} NODE;

// 出栈操作,出栈时先取出栈顶元素的值，在修改栈顶指针，释放原栈顶结点
NODE *popstack(NODE *top, int *p)
{
    NODE *q;         // 定义q结点
    if (top != NULL) // 如果栈不为空
    {
        q = top;
        *p = top->data;  // 将栈顶元素放入*p中
        top = top->next; // 修改top指针
        free(q);         // 释放原栈顶空间
    }
    return q; // 返回栈顶指针
}

  • 老规矩：图文并茂

    image-20220219205046478

3.3 队列_顺序存储

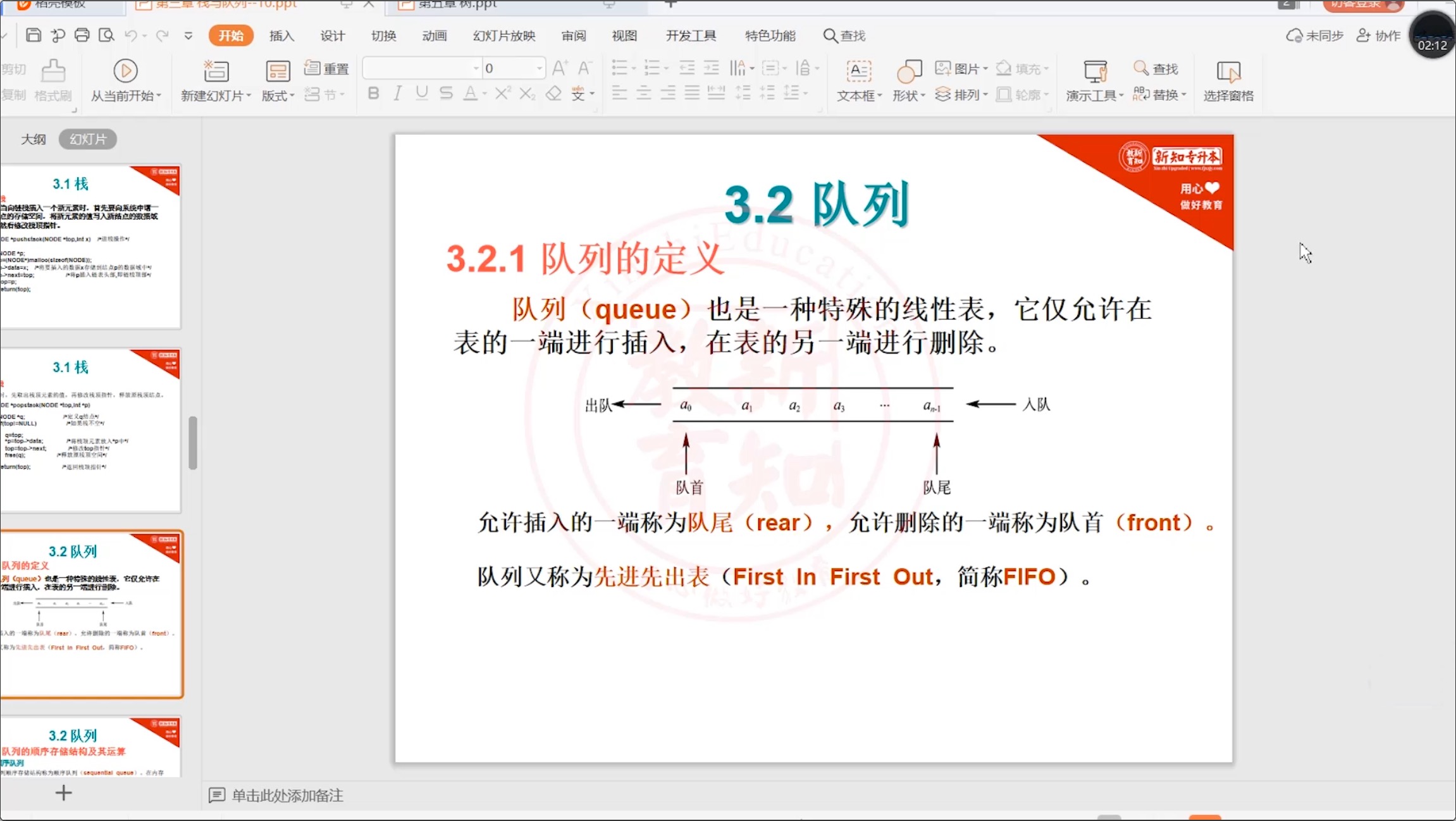
3.3.1 队列_相关概述

image-20220219205430321

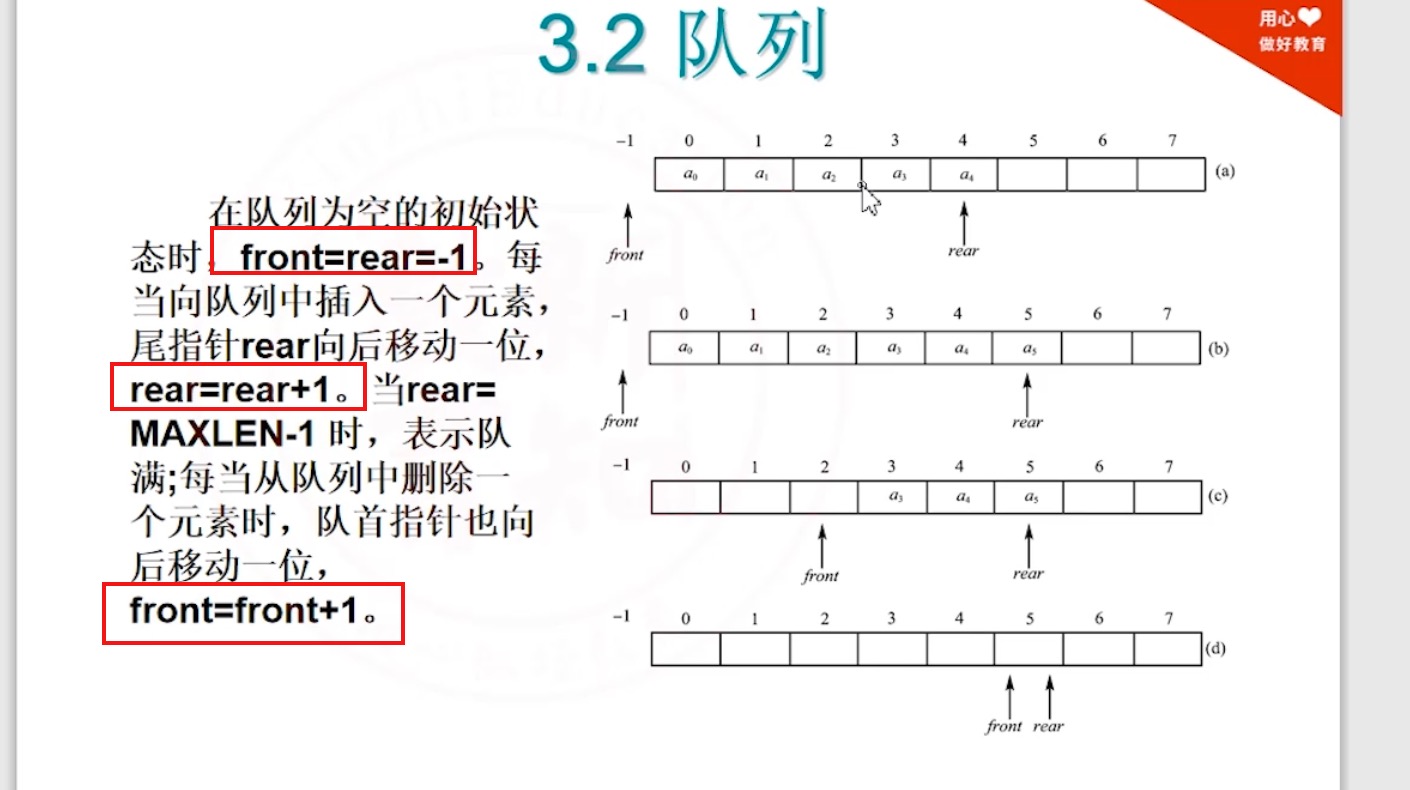
3.3.2 顺序队列_定义

image-20220219205831600

#include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 顺序队列的结构定义
typedef struct
{
    elementType data[MAXLEN]; // 存放队列元素的数组
    int front, rear;          // 队列头、尾指针
} SeQueue;

image-20220219212025379

3.3.3 顺序队列_取头元素

  • C语言版代码

    #include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 顺序队列的结构定义
typedef struct
{
    elementType data[MAXLEN]; // 存放队列元素的数组
    int front, rear;          // 队列头、尾指针
} SeQueue;

// 取队列头元素，若队列0非空，用 *x 返回其元素
int getFront_sq(SeQueue *q, elementType *x)
{
    if (q->front == q->rear)  // 判断队列是否为空
    {
        return 0;   // 队列空返回0
    }
    else
    {
        *x = q->data[(q->front) + 1];
        return 1;
    }
}

    ?

3.3.4 顺序队列_入队

  • C语言版代码

    #include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 顺序队列的结构定义
typedef struct
{
    elementType data[MAXLEN]; // 存放队列元素的数组
    int front, rear;          // 队列头、尾指针
} SeQueue;

// 入队
int Enqueue_sq(SeQueue *q, elementType x) {
    if (q ->rear == MAXLEN - 1) {
        return 0;   // 队列满返回0
    }
    q->rear++;
    q->data[q->rear] = x;
    return 1;
}

3.3.5 顺序队列_出队

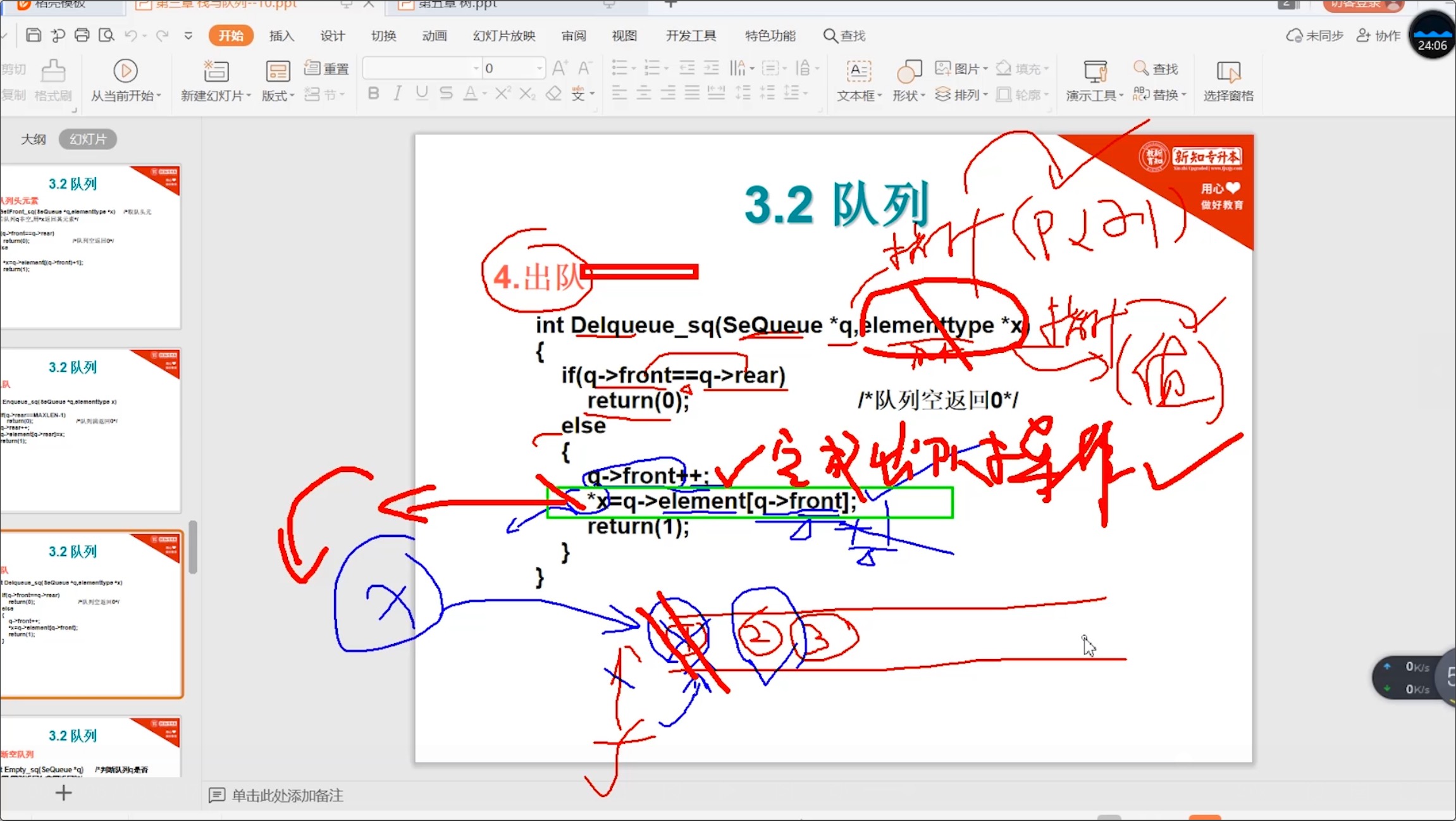
  • C语言版代码

    #include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 顺序队列的结构定义
typedef struct
{
    elementType data[MAXLEN]; // 存放队列元素的数组
    int front, rear;          // 队列头、尾指针
} SeQueue;

// 出队
int Delqueue_sq(SeQueue *q, elementType *x)
{
    if (q->rear == q->front)
    {
        return 0; // 队列空返回0
    }
    q->front++;
    *x = q->data[q->front];
    return 1;
}

image-20220219211637801

3.4 循环队列【重点】

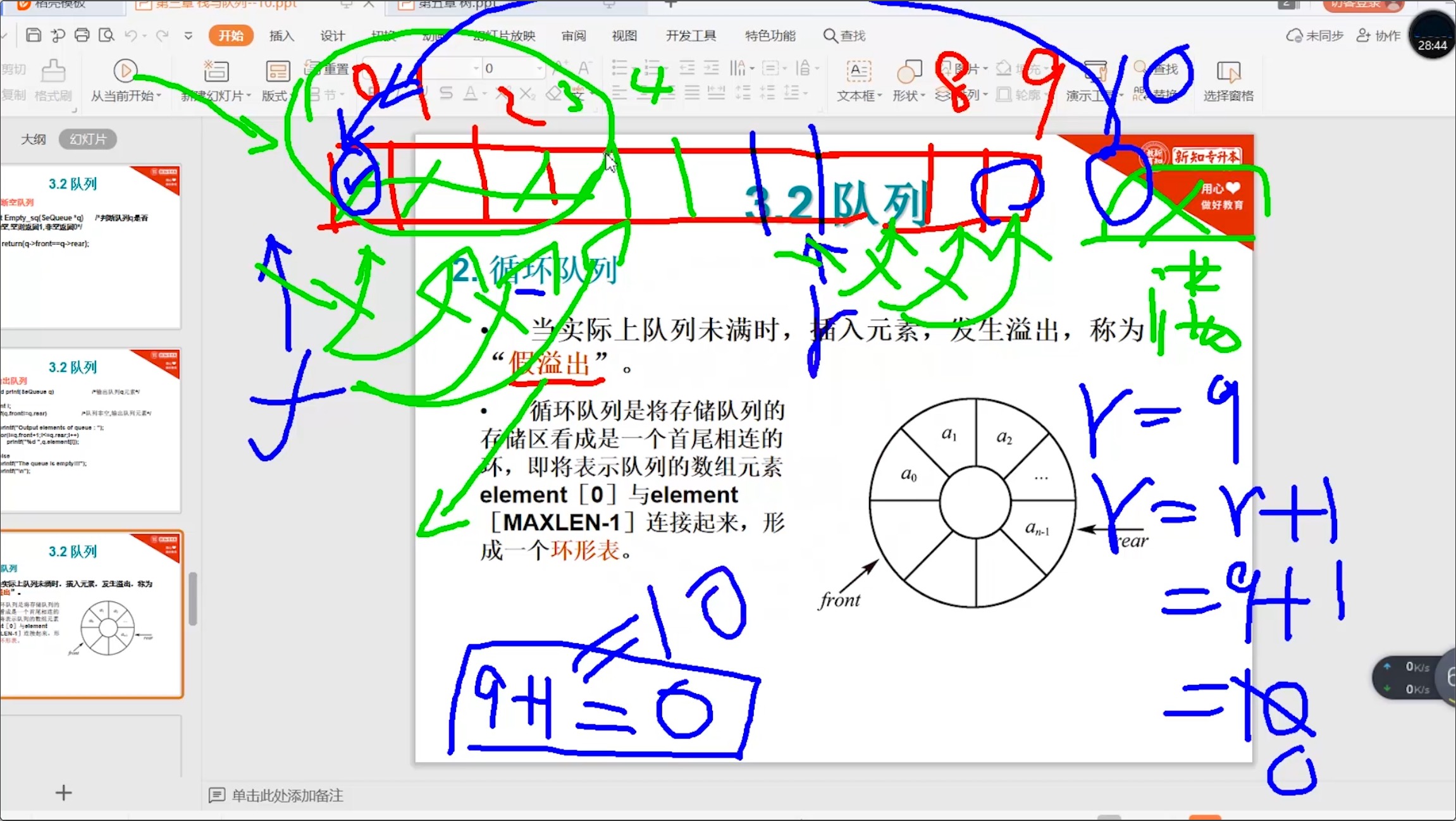
3.4.1 循环队列_概念

image-20220219212119995

image-20220220133549222

3.4.2 循环队列_入队

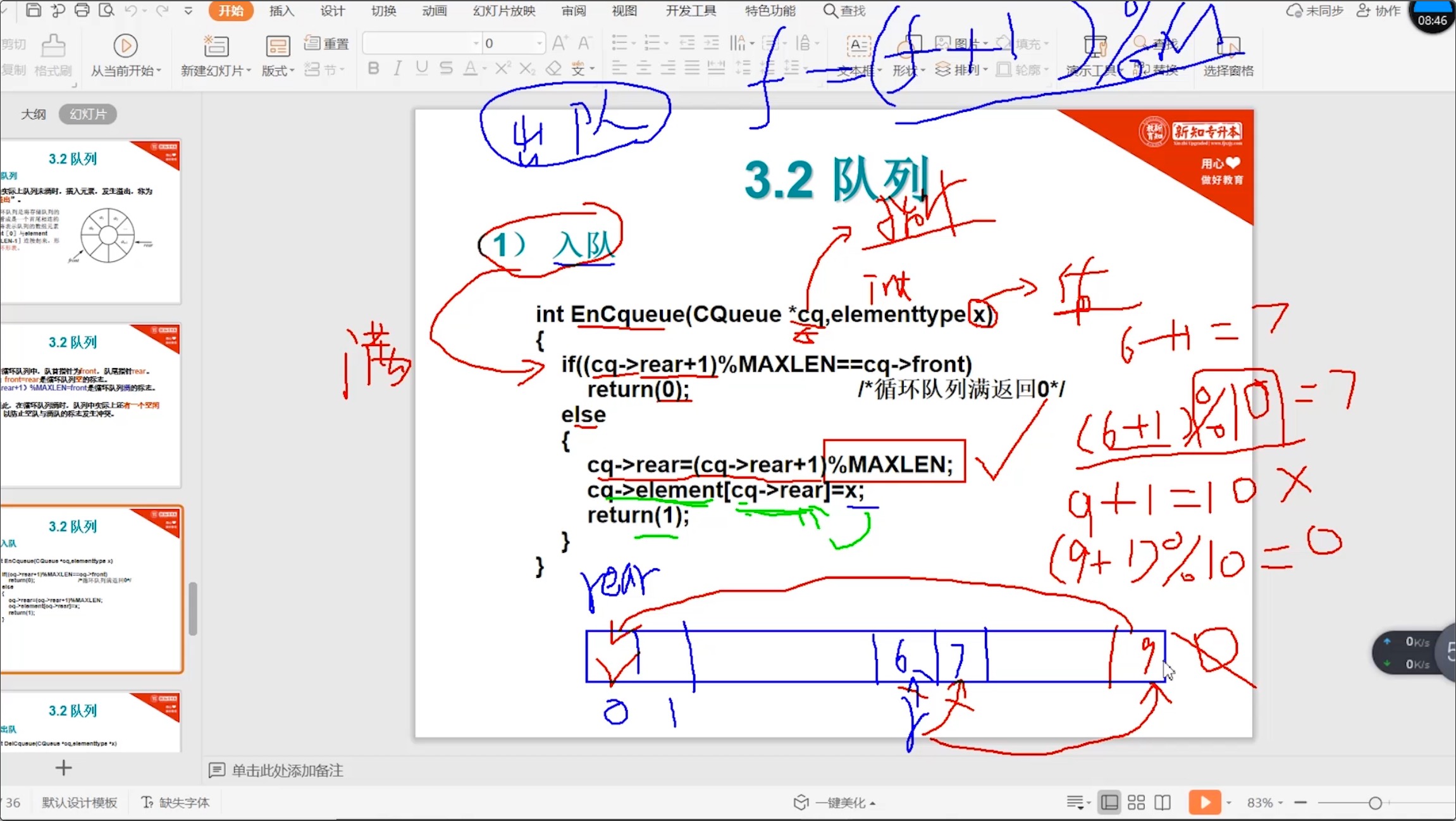
  • 代码

    #include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 循环队列的结构定义
typedef struct
{
    elementType data[MAXLEN]; // 存放队列元素的数组
    int front, rear;          // 队列头、尾指针
} CQueue;

// 循环队列_入队
int EnCqueue(CQueue *cq, elementType x)
{
    if ((cq->rear + 1) % MAXLEN == cq->front)  // 判断循环队列是否为满
    {
        return 0;   
    }
    else
    {
        cq->rear = (cq->rear + 1) % MAXLEN;
        cq->data[cq->rear] = x;
        return 1;
    }
}

  • 图文讲解

    image-20220220134427789

3.4.3 循环队列_出队

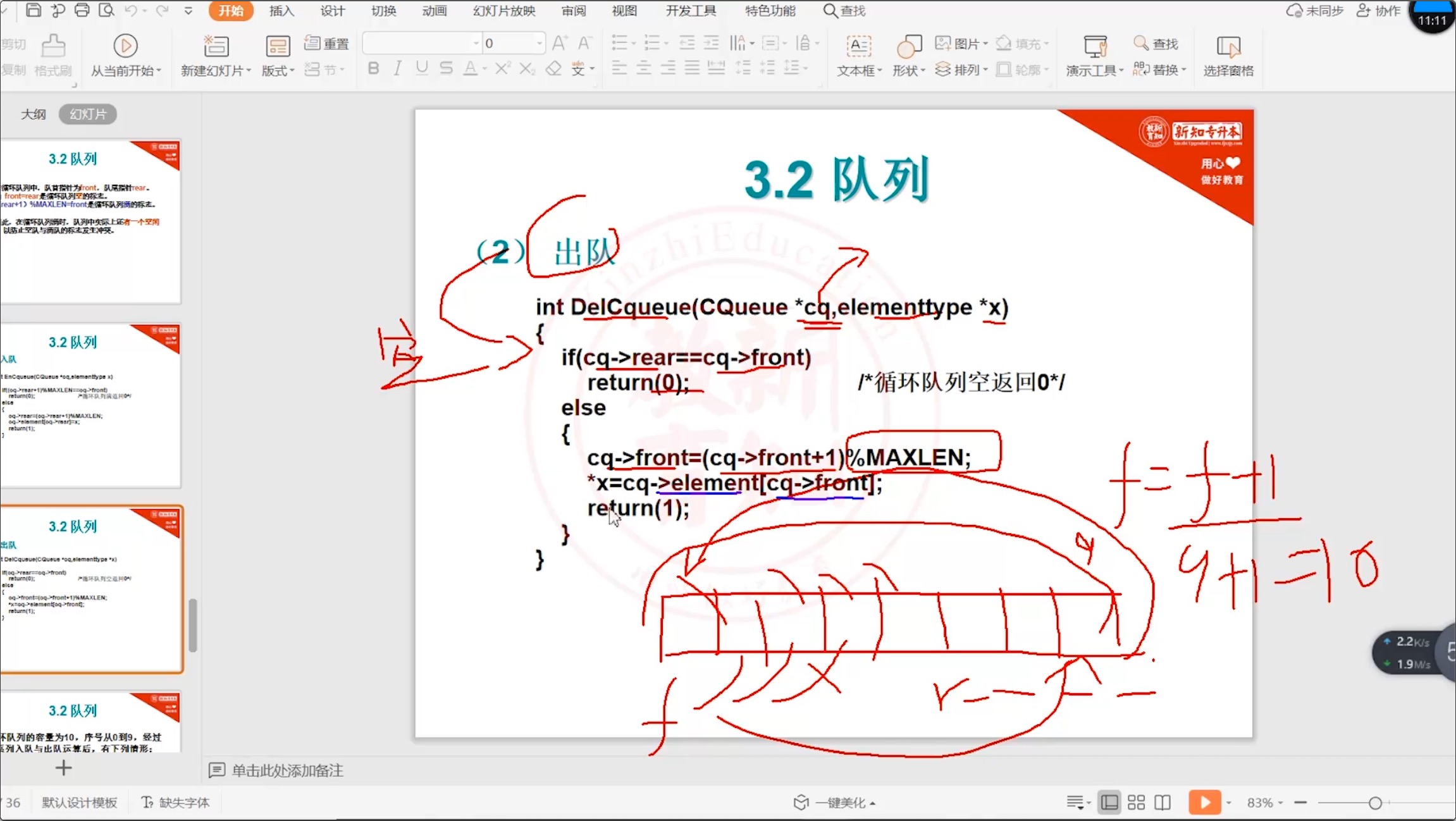
  • 代码

    #include <stdio.h>
#define MAXLEN 10
typedef int elementType;

// 循环队列的结构定义
typedef struct
{
    elementType data[MAXLEN]; // 存放队列元素的数组
    int front, rear;          // 队列头、尾指针
} CQueue;

// 循环队列_出队
int DelCqueue(CQueue *cq, elementType *x)
{
    if (cq->rear == cq->front) // 判断循环队列是否为空
        return 0;
    else
    {
        cq->front = (cq->front + 1) % MAXLEN;
        *x = cq->data[cq->front];
        return 1;
    }
}

  • 图文讲解

    image-20220220135446821

3.4.4 循环队列_求元素个数

  • 循环队列_求元素个数的公式：(rear - front + maxLen) % maxLen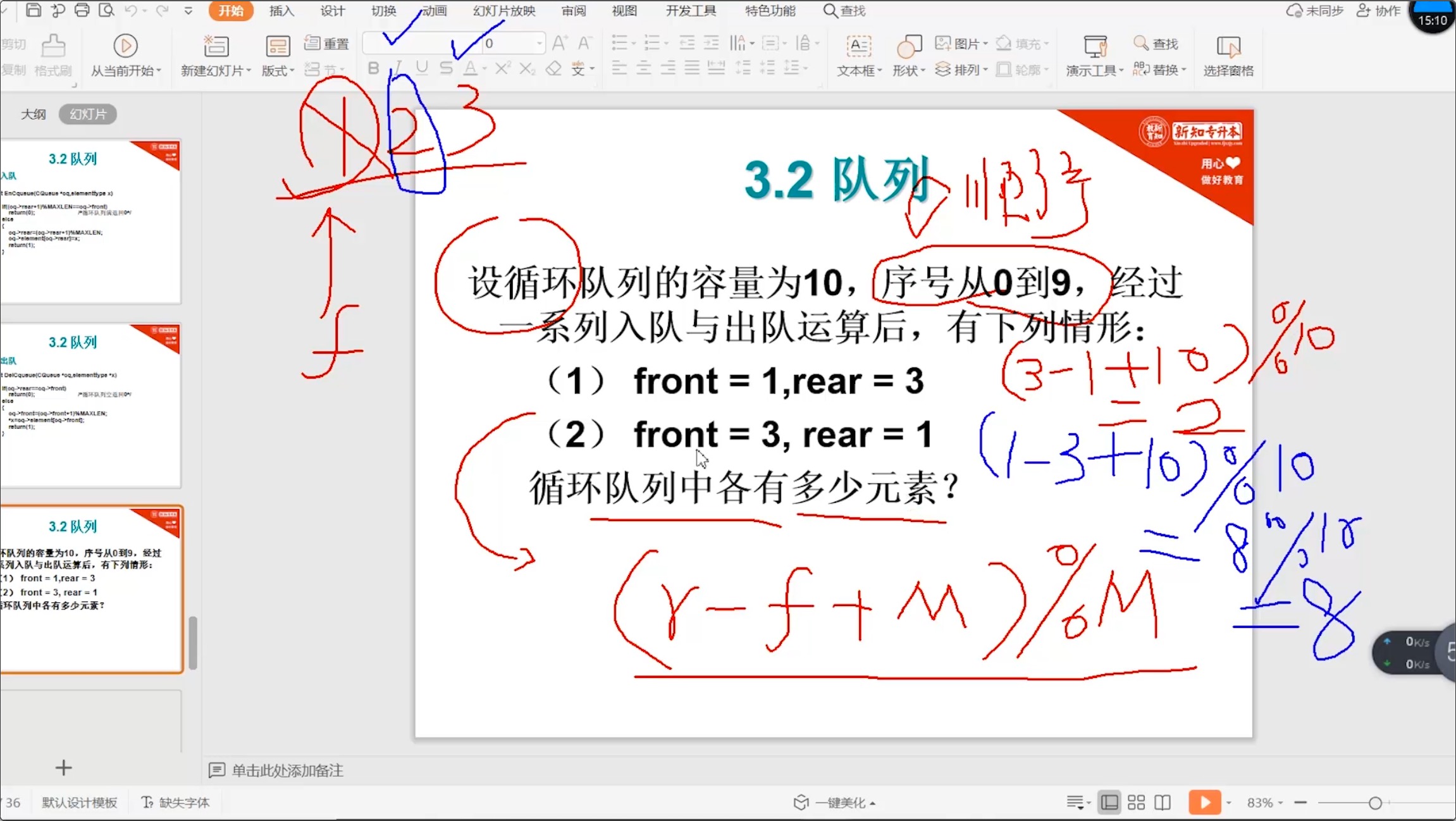

    image-20220220135852064

3.5 队列_链式存储

3.5.1 链队列_入队

  • 代码

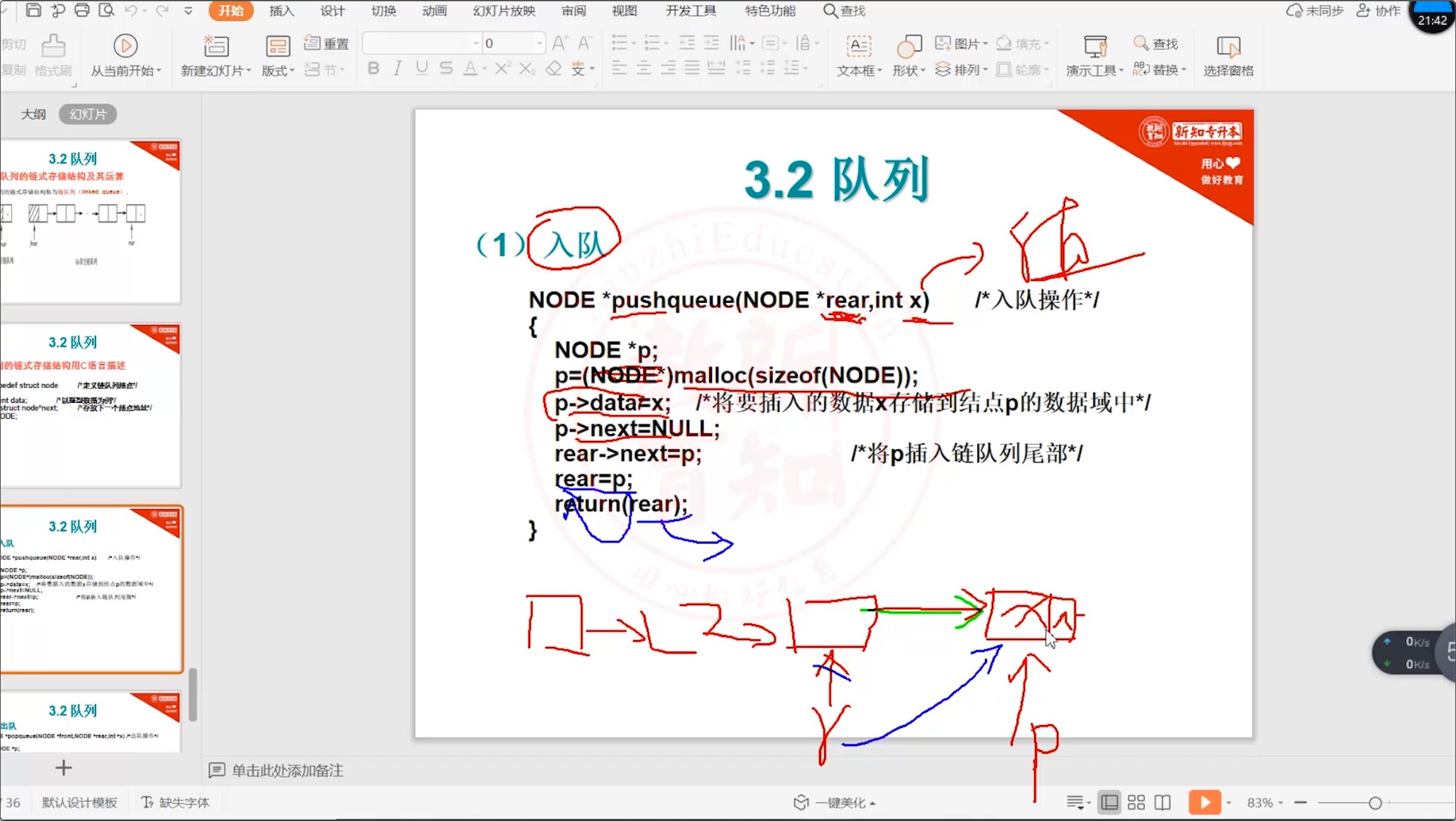
    #include <stdio.h>
#include <stdlib.h>

// 定义链队列结点
typedef struct node
{
    int data;         // 当前结点的地址值
    struct node *next // 下一个结点地址值
} NODE;

// 入队
NODE *pushqueue(NODE *rear, int x)
{
    NODE *p;
    p = malloc(sizeof(NODE));
    p->data = x; // 将要插入的数据x存储到结点p的数据域中
    p->next = NULL;
    rear->next = p; // 将p插入链队列尾部
    rear = p;
    return rear;
}

  • 讲解

    image-20220220140556837

3.5.2 链队列_出队

  • 代码

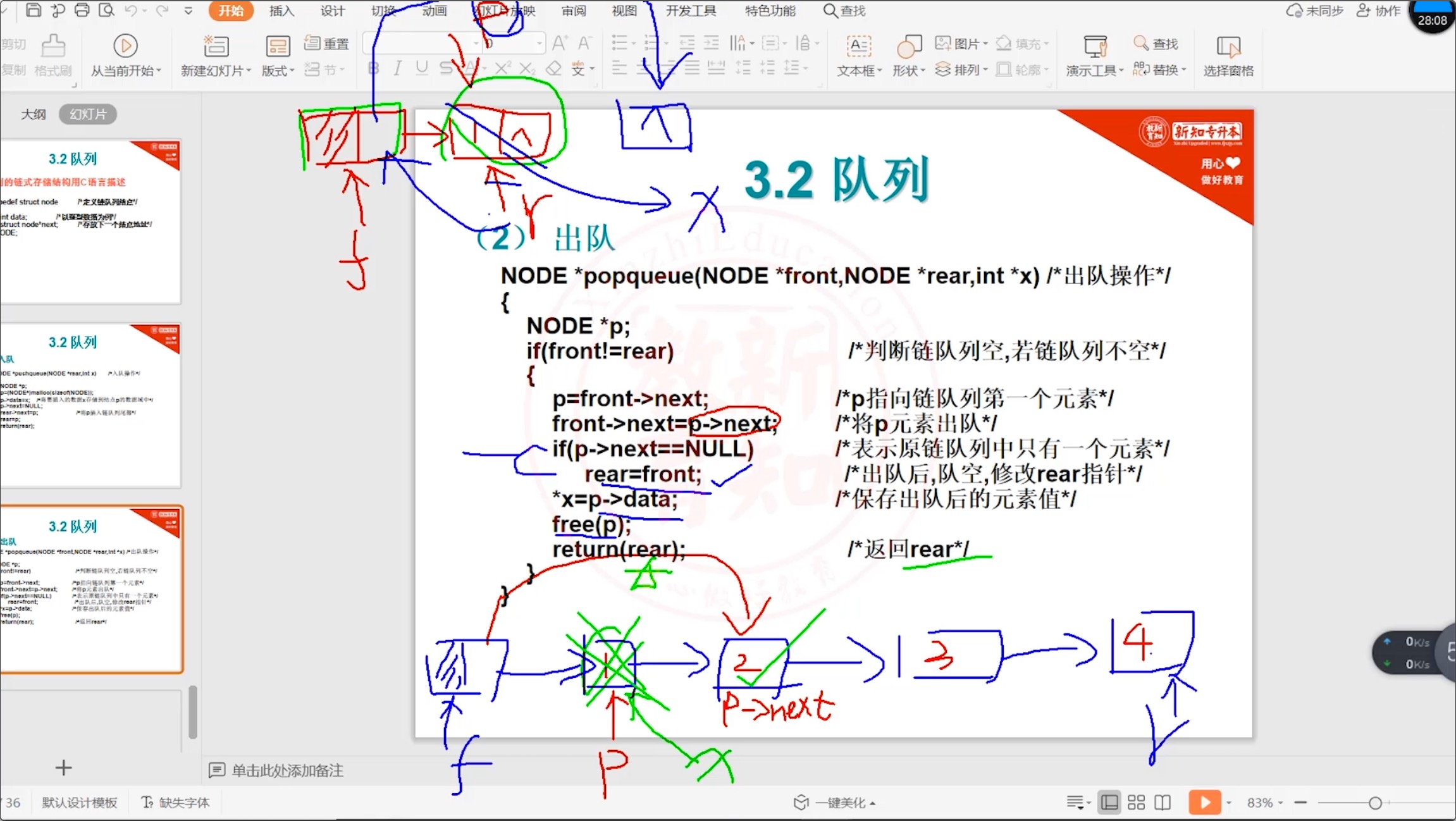
    #include <stdio.h>
#include <stdlib.h>

// 定义链队列结点
typedef struct node
{
    int data;         // 当前结点的地址值
    struct node *next // 下一个结点地址值
} NODE;

// 出队
NODE *popqueue(NODE *front, NODE *rear, int *x)
{
    NODE *p;
    if (front != rear) // 判断链队列是否为空
    {
        p = front->next;       // p指向链队列第一个元素
        front->next = p->next; // 将p元素出队
        if (p->next == NULL)   // 表示原链队列中只有一个元素
            rear = front;      // 出队后，队空，修改rear指针
        *x = p->data;          // 保存出队后的元素值
        free(p);               // 释放空间
        return rear;
    }
}

  • 讲解

    image-20220220141422878

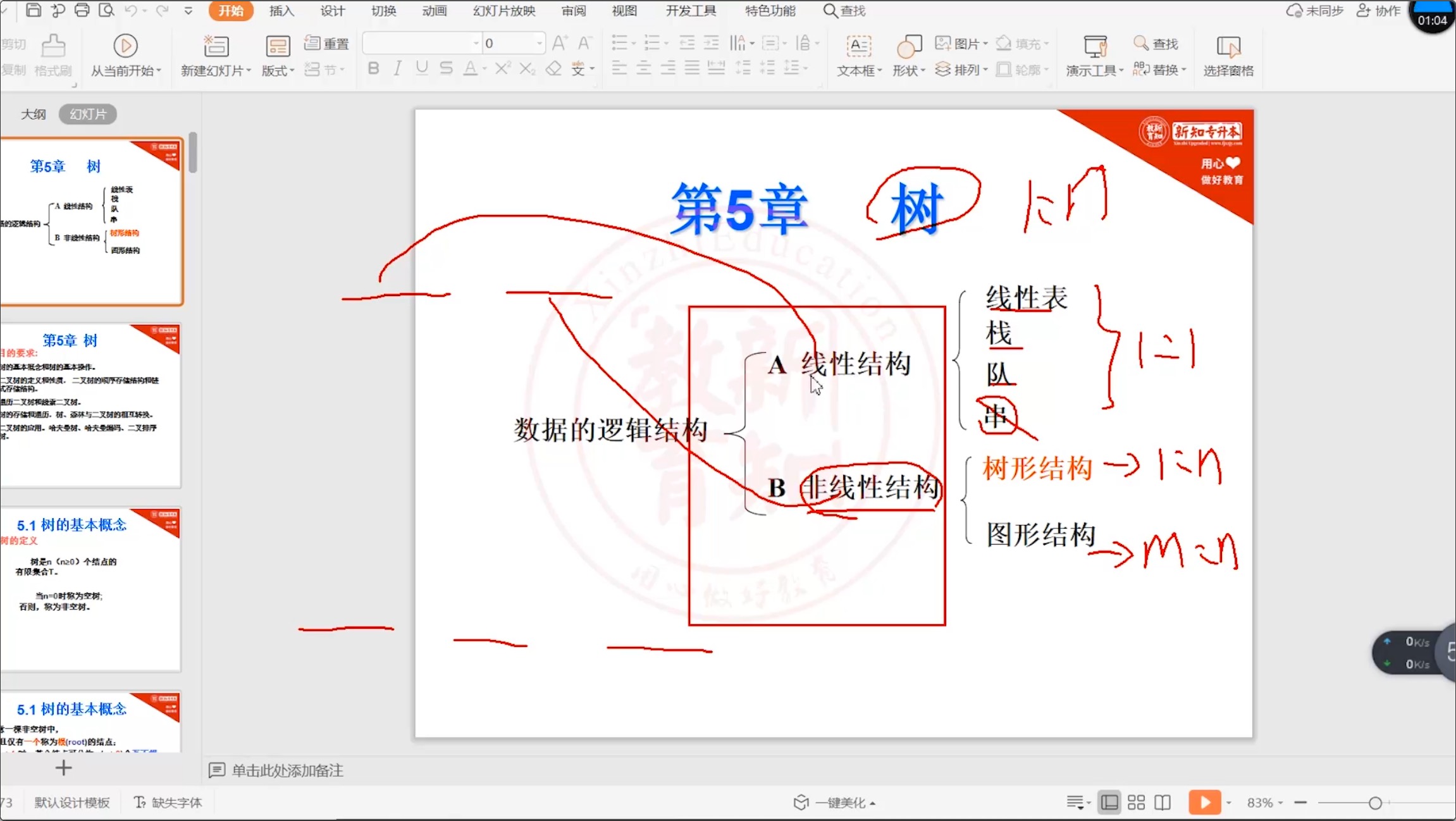
第 5 章 - 树

image-20220220155638096

5.1 树的基本概念

5.1.1 树的定义

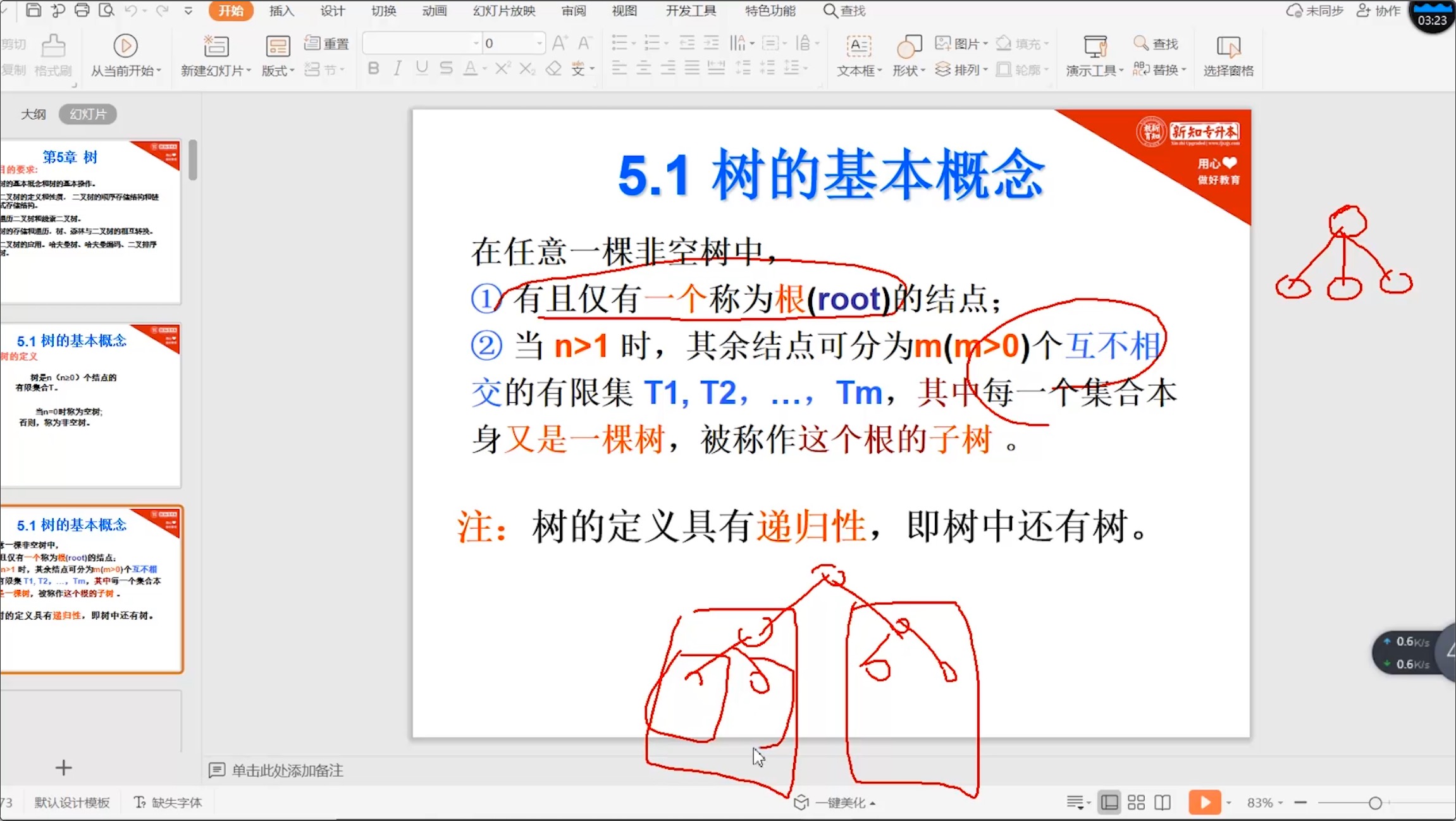
image-20220220155852196

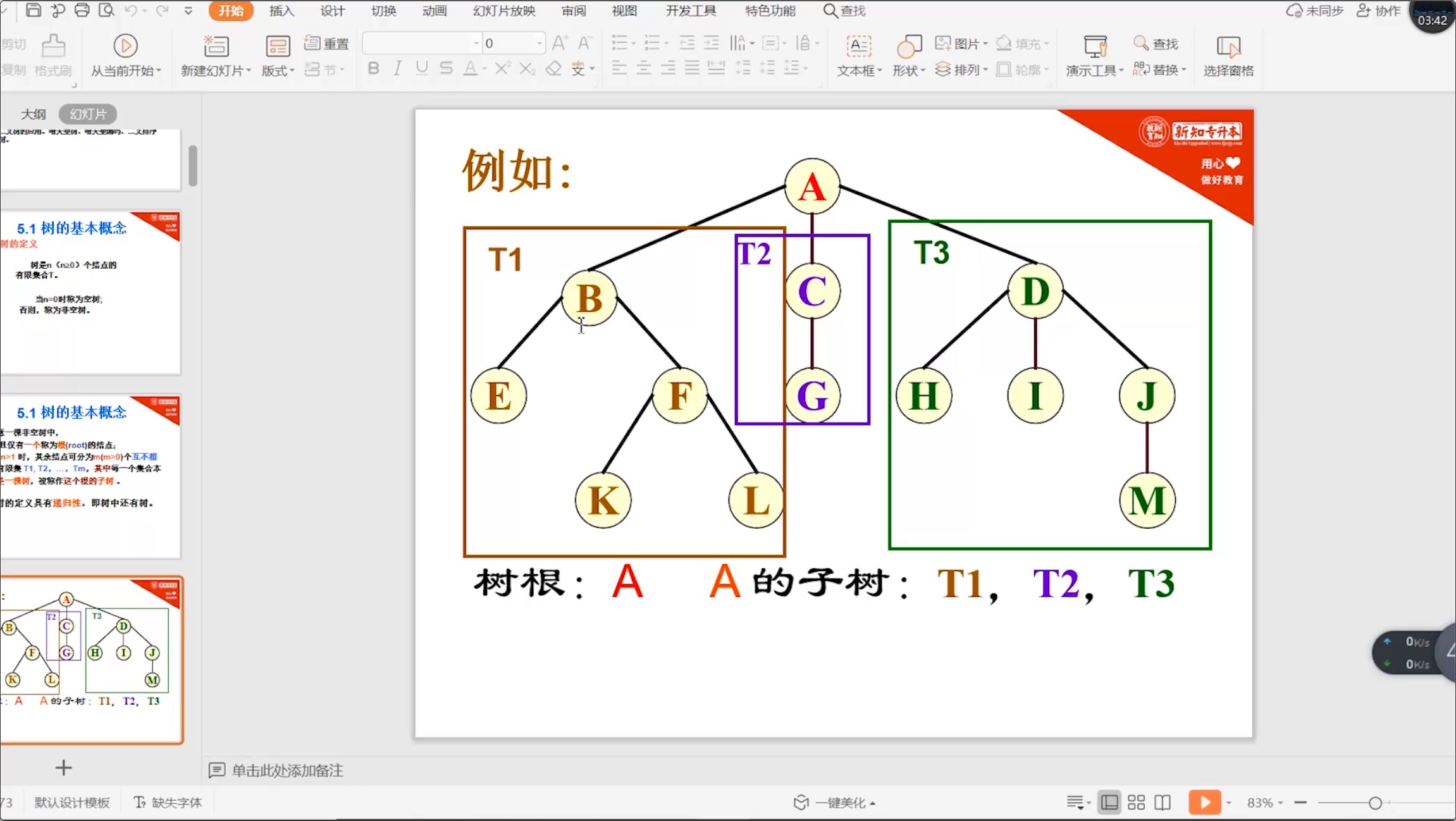
image-20220220155904289

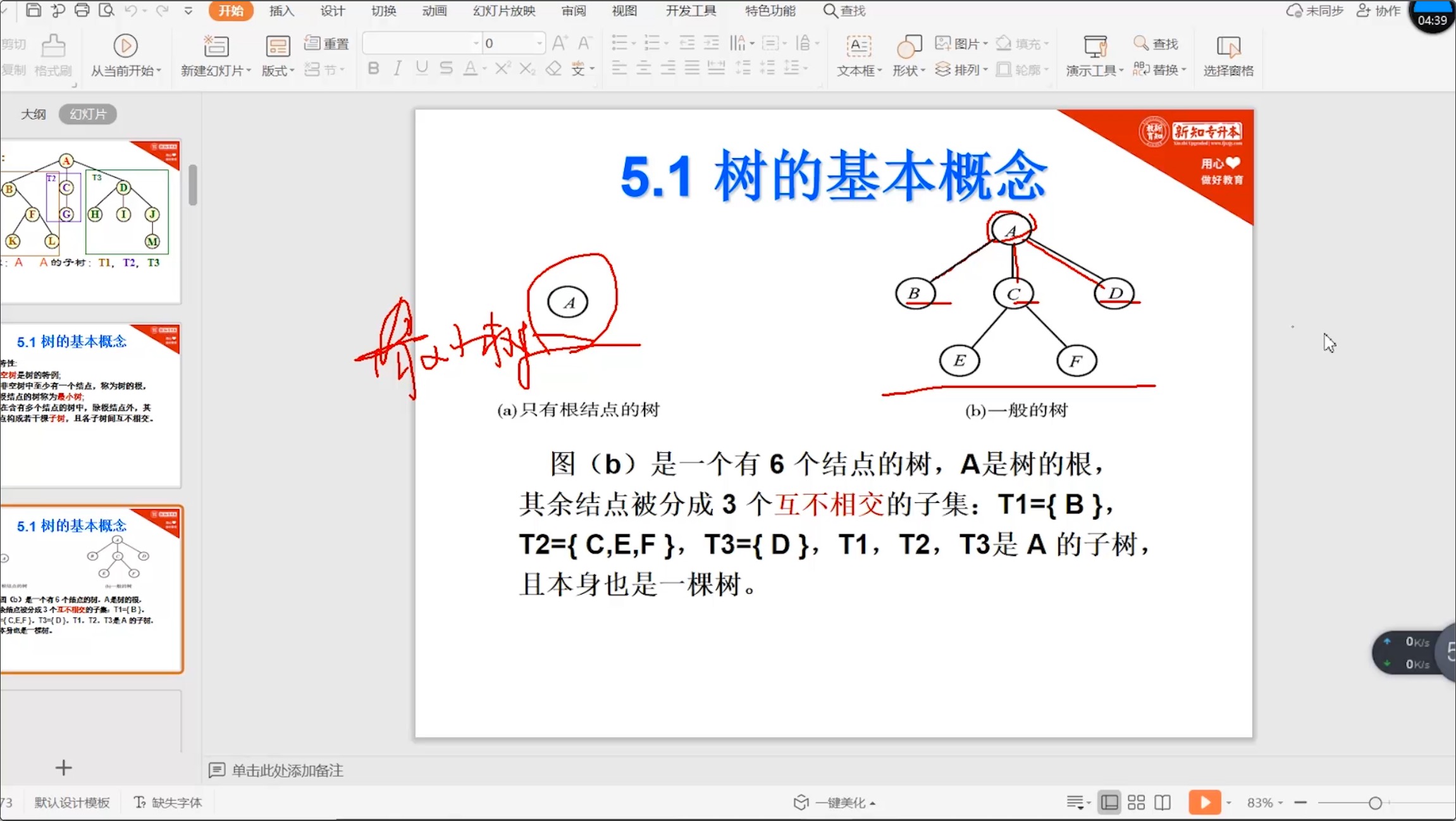
image-20220220155942164

5.1.2 树的相关术语

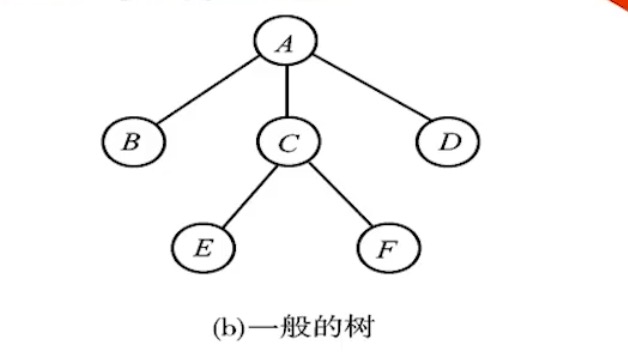
image-20220220160532789

  • A结点是BCD结点的双亲，BCD结点是A结点的孩子

  • A结点有三个孩子，所以他的度为3，B结点下没有孩子，所以他的度为0，C结点度为2

  • 树的度：将所有结点的度算出来，然后取最大的度，比如上图中最大的度是3

  • 树的度决定了该树是几叉树，比如上图树的度为3，则该树是一个三叉树

  • 根节点：无双亲，无兄弟

  • 没有孩子的结点度为0，这样的结点也被称为***叶子结点或终端结点***

  • 真祖先：E结点的真祖先是AC

  • 兄弟：***同一双亲的孩子***结点之间互为兄弟

  • 树的层次、树的深度或高度

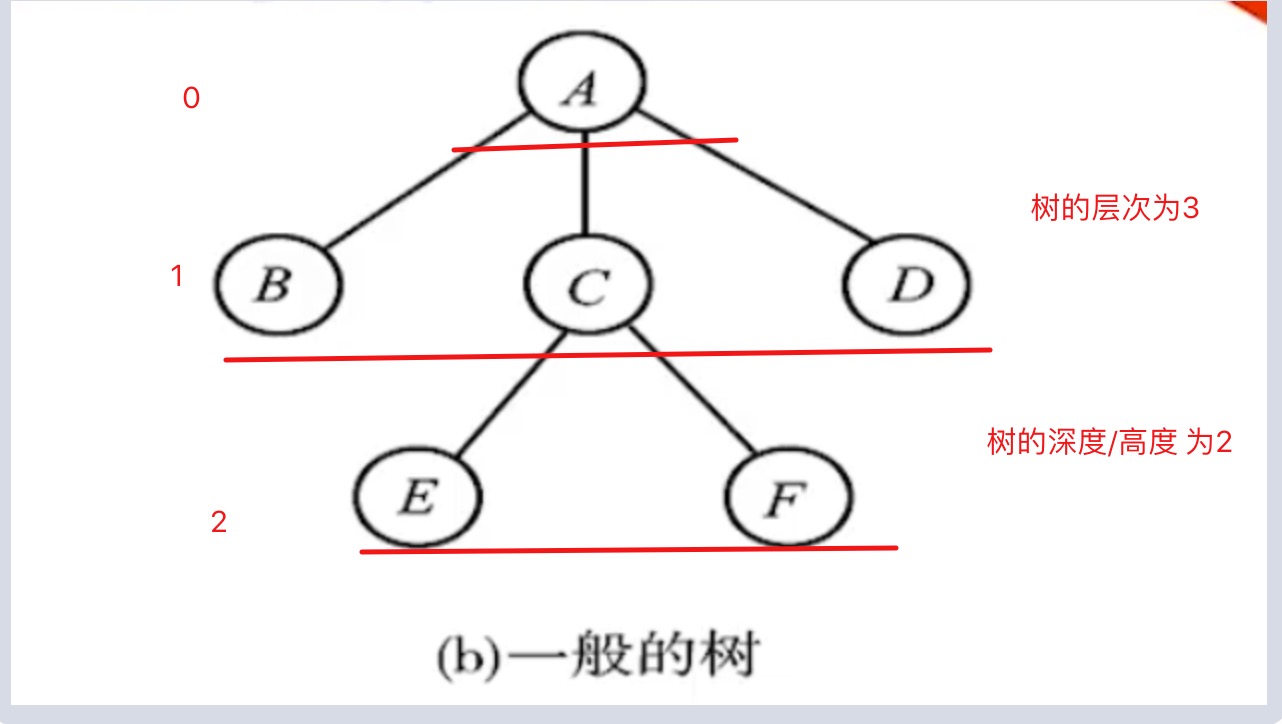
    image-20220220161530732

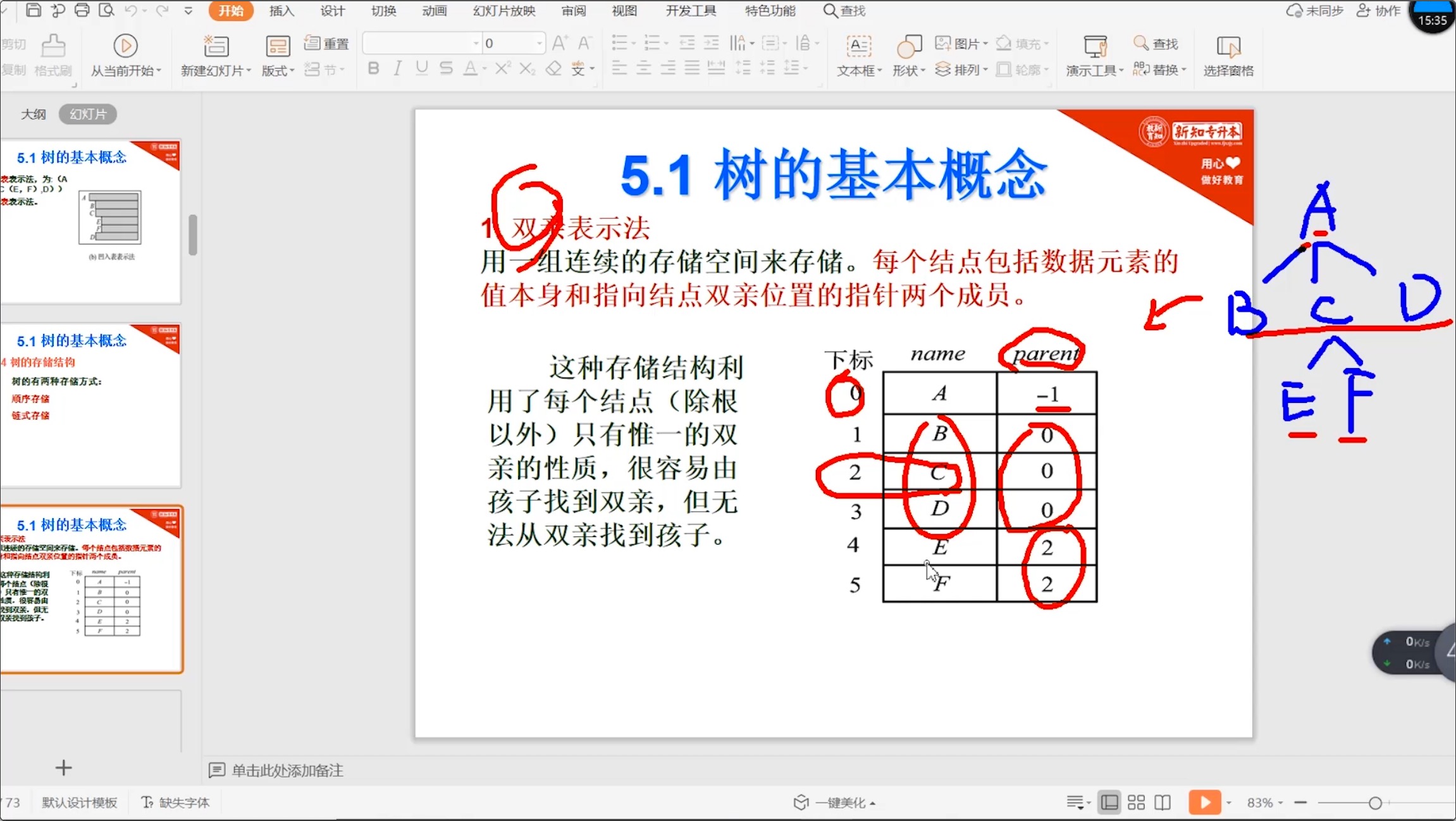
5.2.3 树_双亲表示法

image-20220220161906576

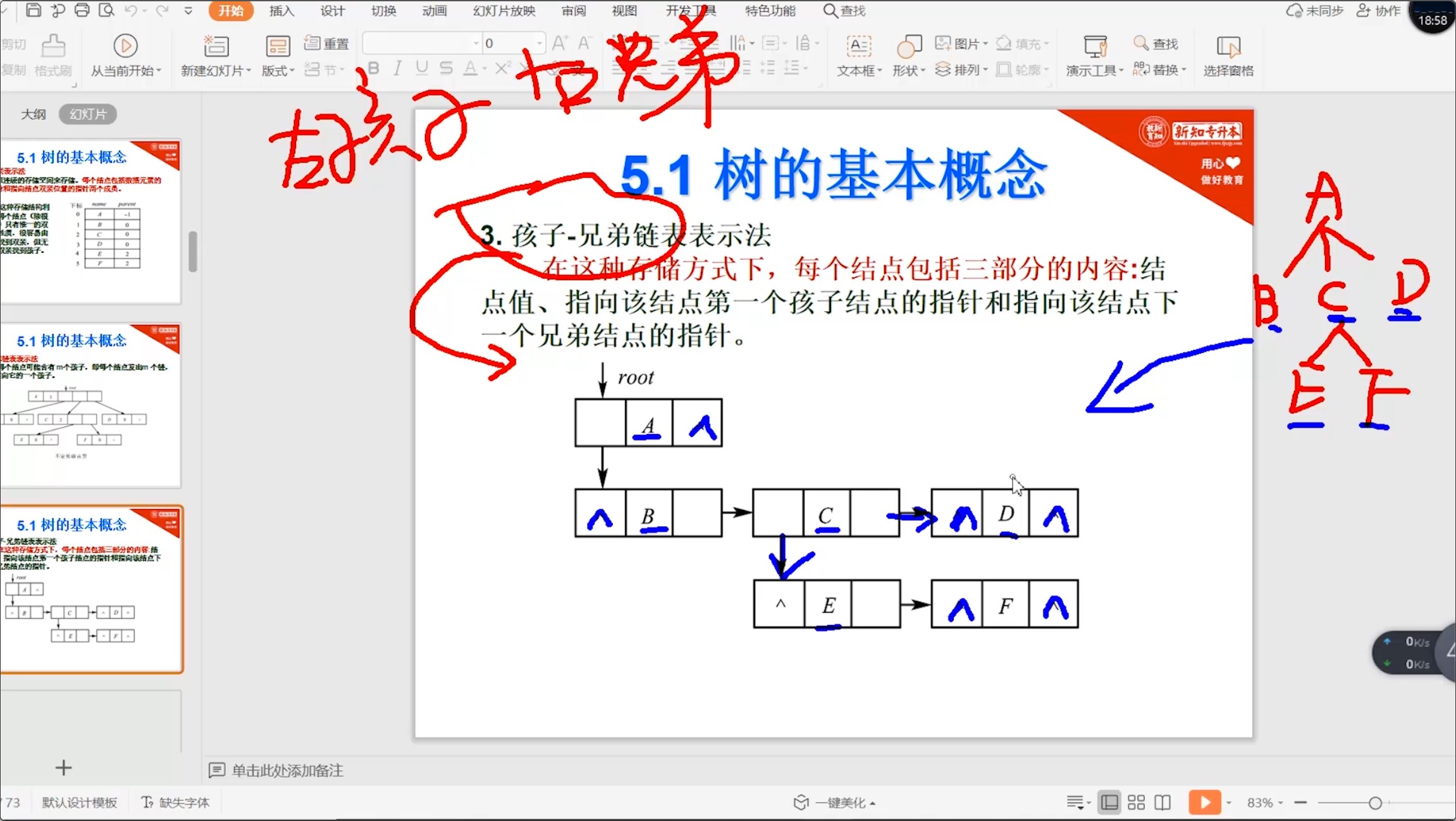
5.2.4 孩子-兄弟链表表示法

image-20220220162114548

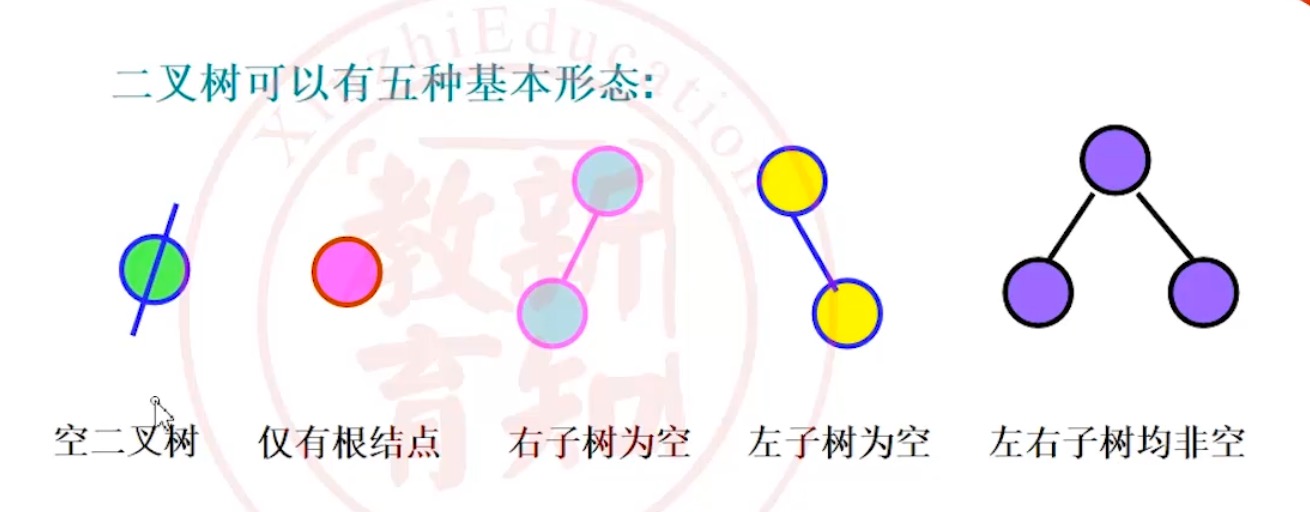
5.2 二叉树

5.2.1 二叉树_概念

image-20220220162238636

image-20220220162304332

5.2.2 二叉树_性质

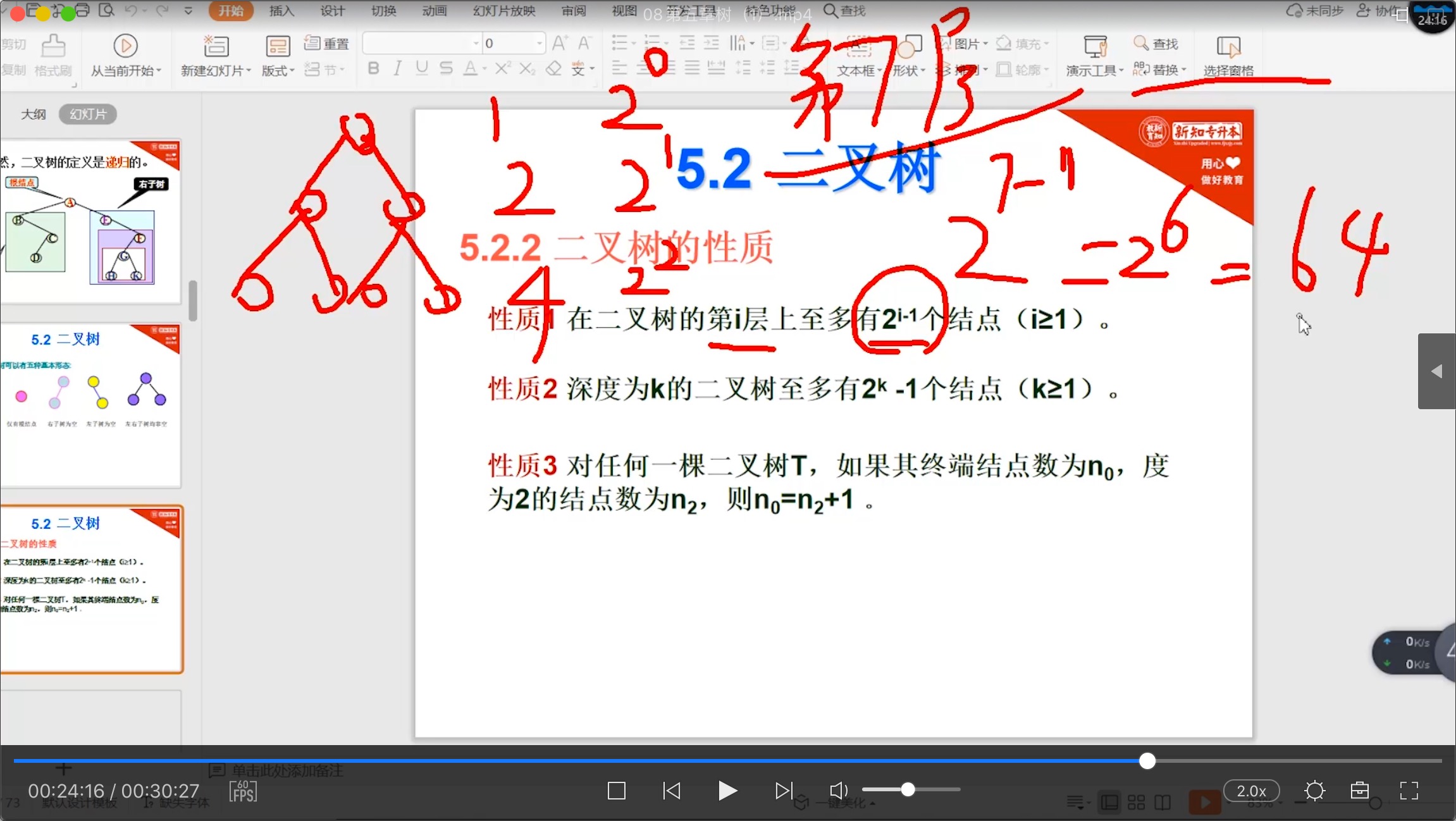
image-20220220162509493

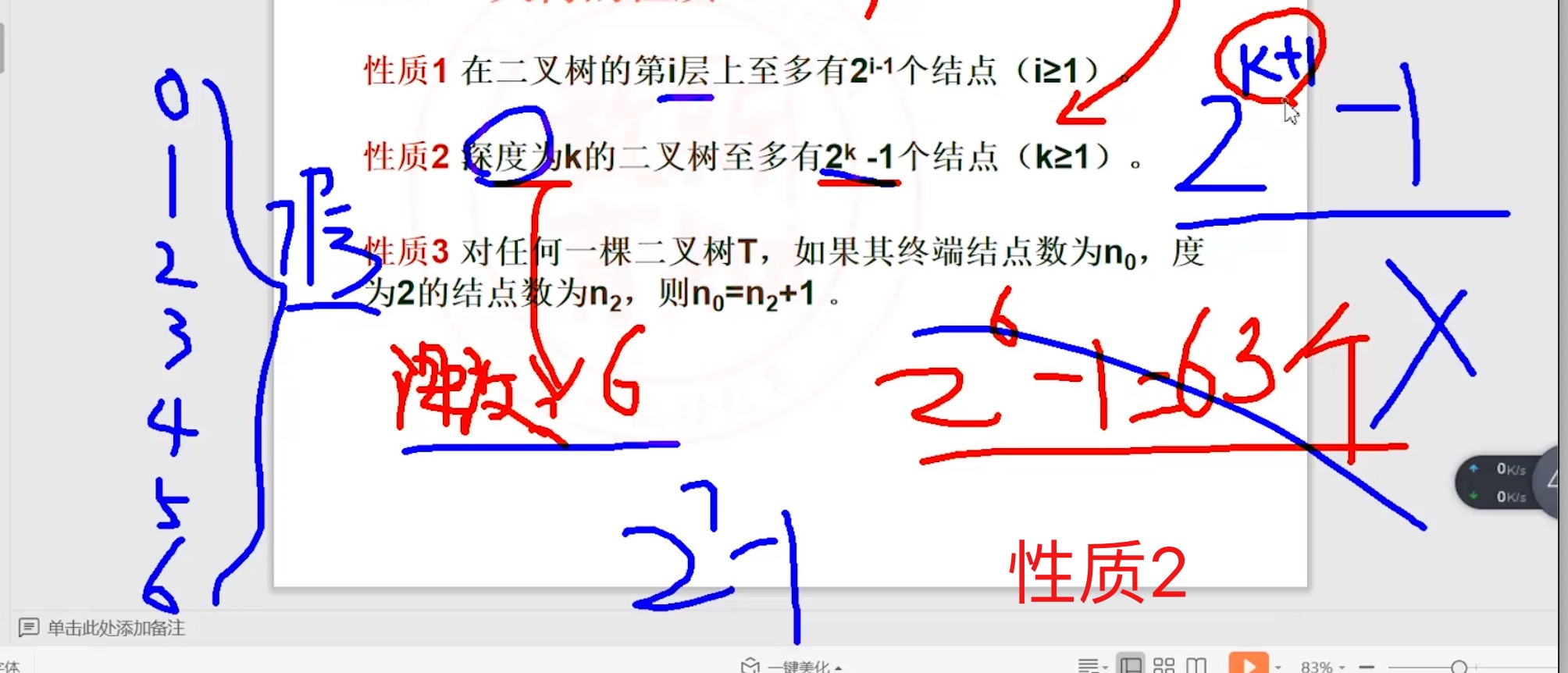
image-20220220162744510

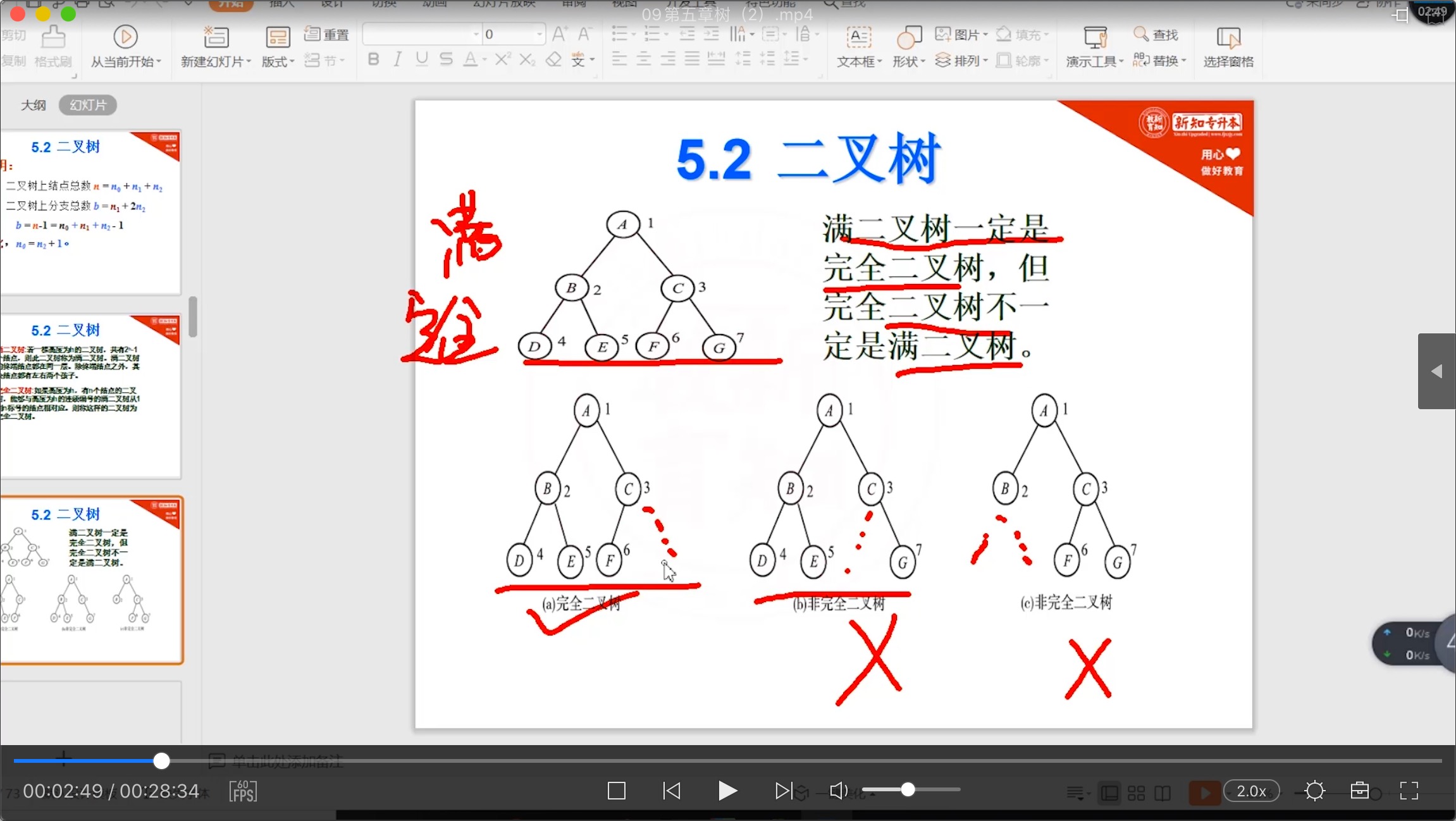
5.2.3 满二叉树和完全二叉树

image-20220220163318512

? image-20220220163330048

5.2.4 完全二叉树_性质

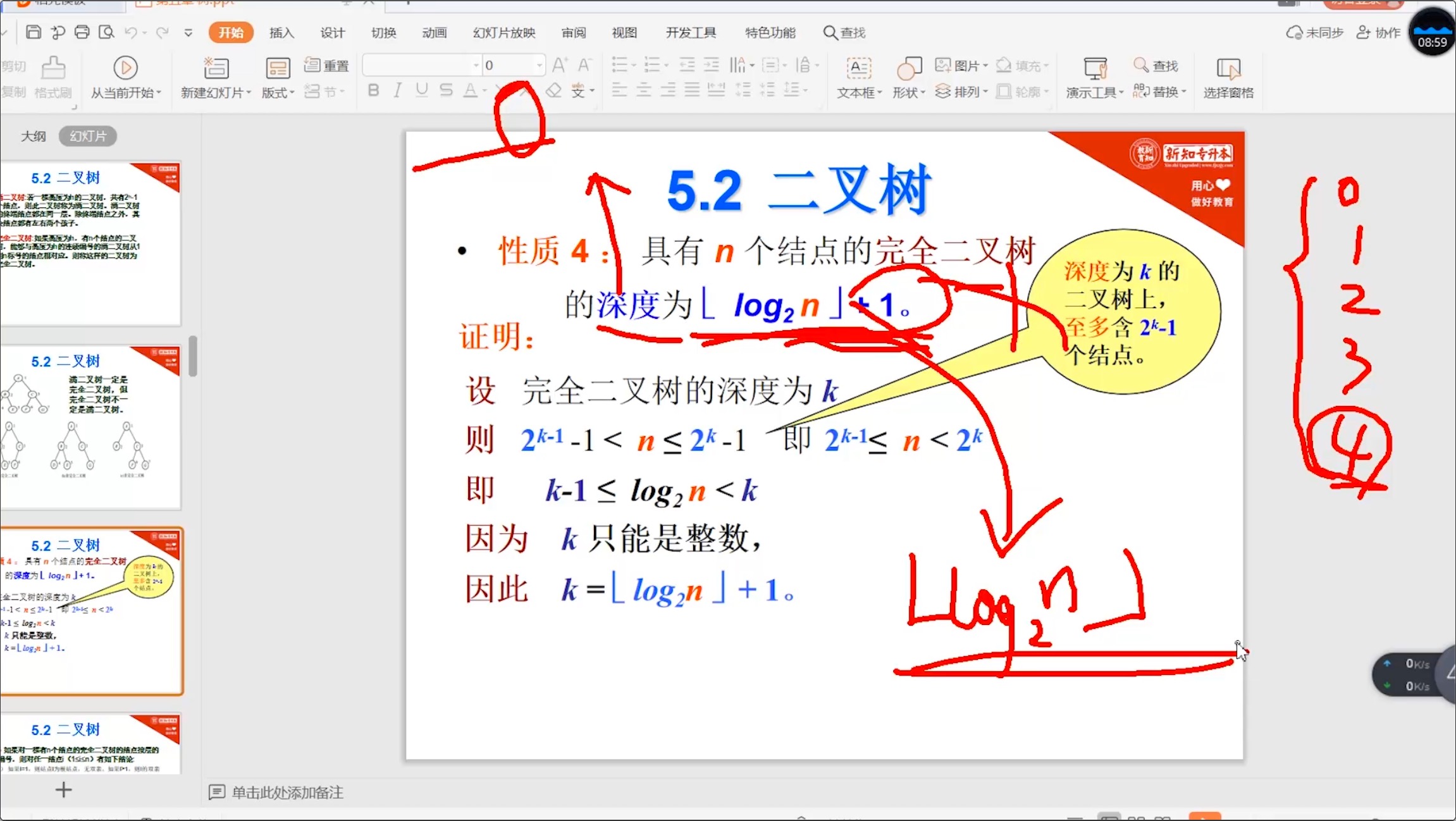
image-20220220163512327

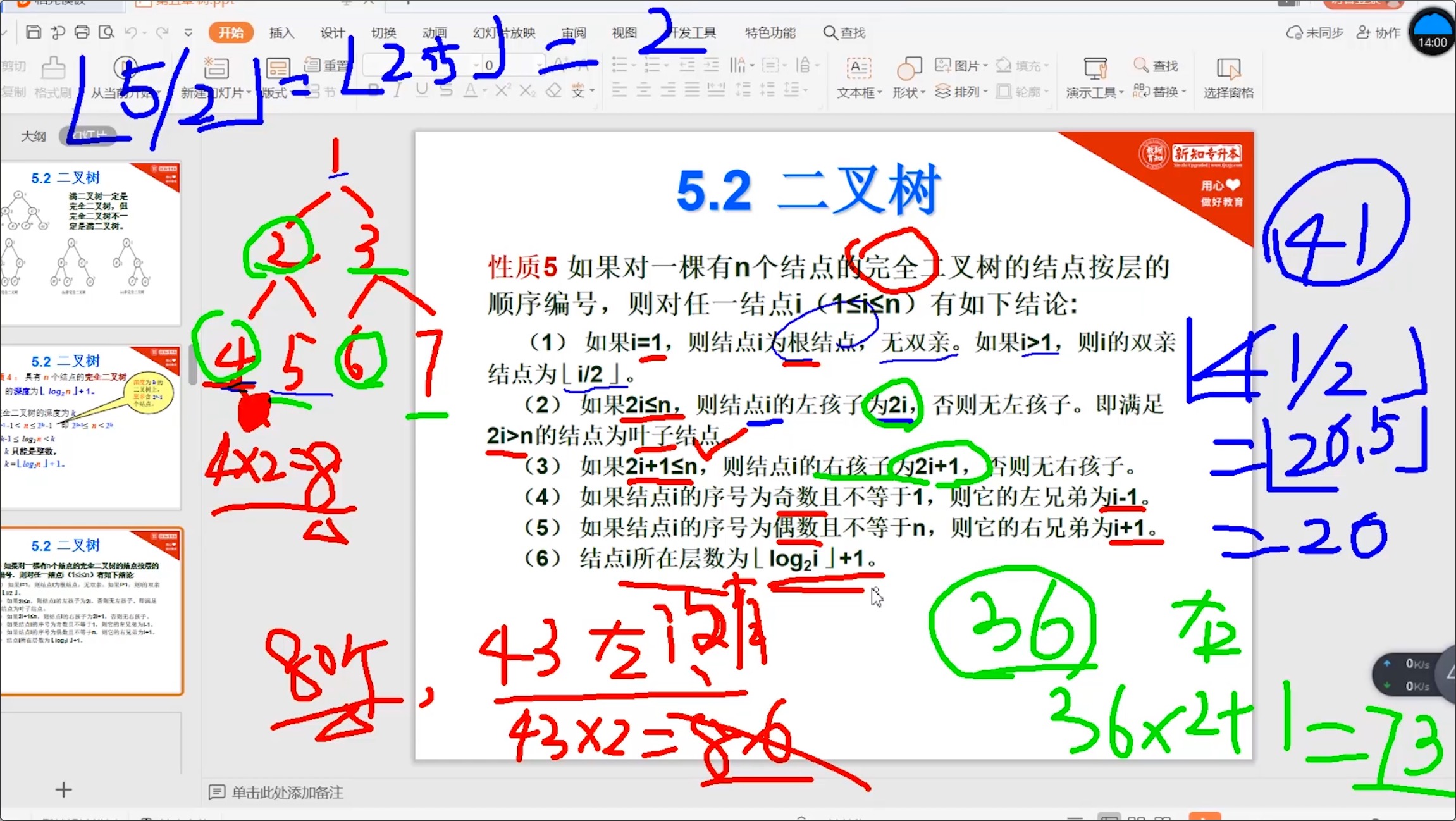
image-20220220163911502

5.3 二叉树的存储结构【重要】

5.3.1 二叉树_顺序存储

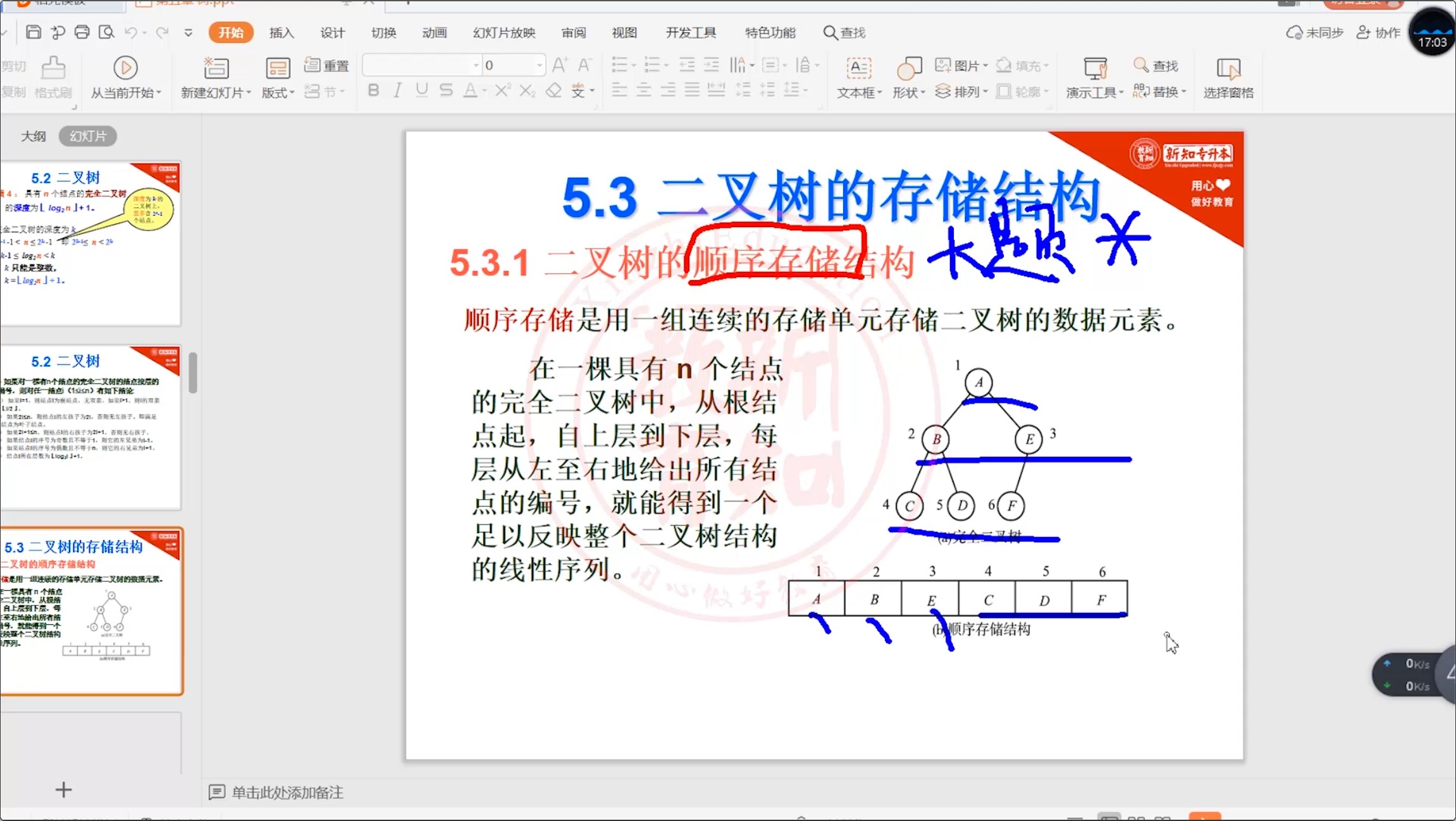
image-20220220164319582

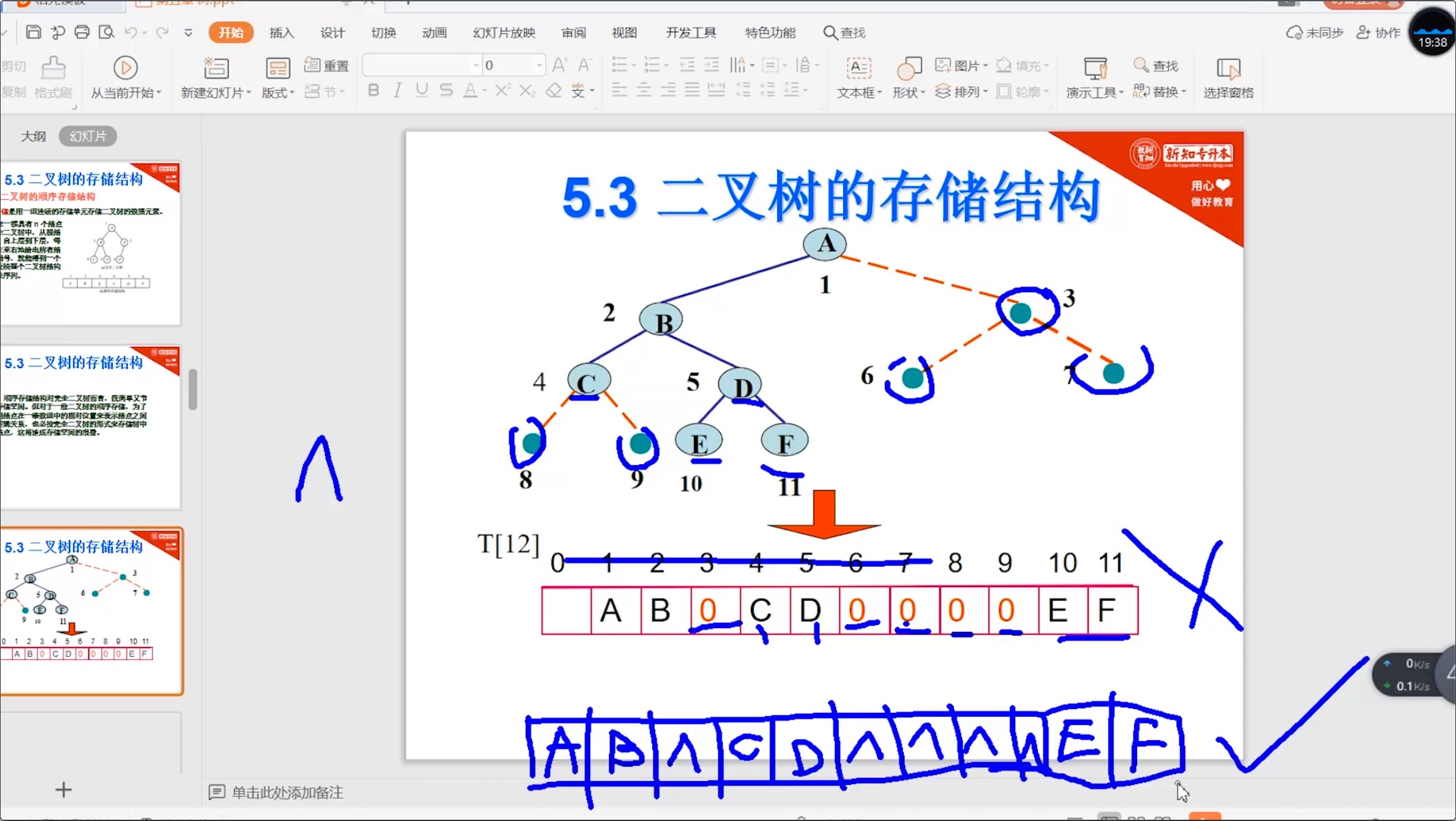
image-20220220164413777

5.3.2 二叉树_链式存储

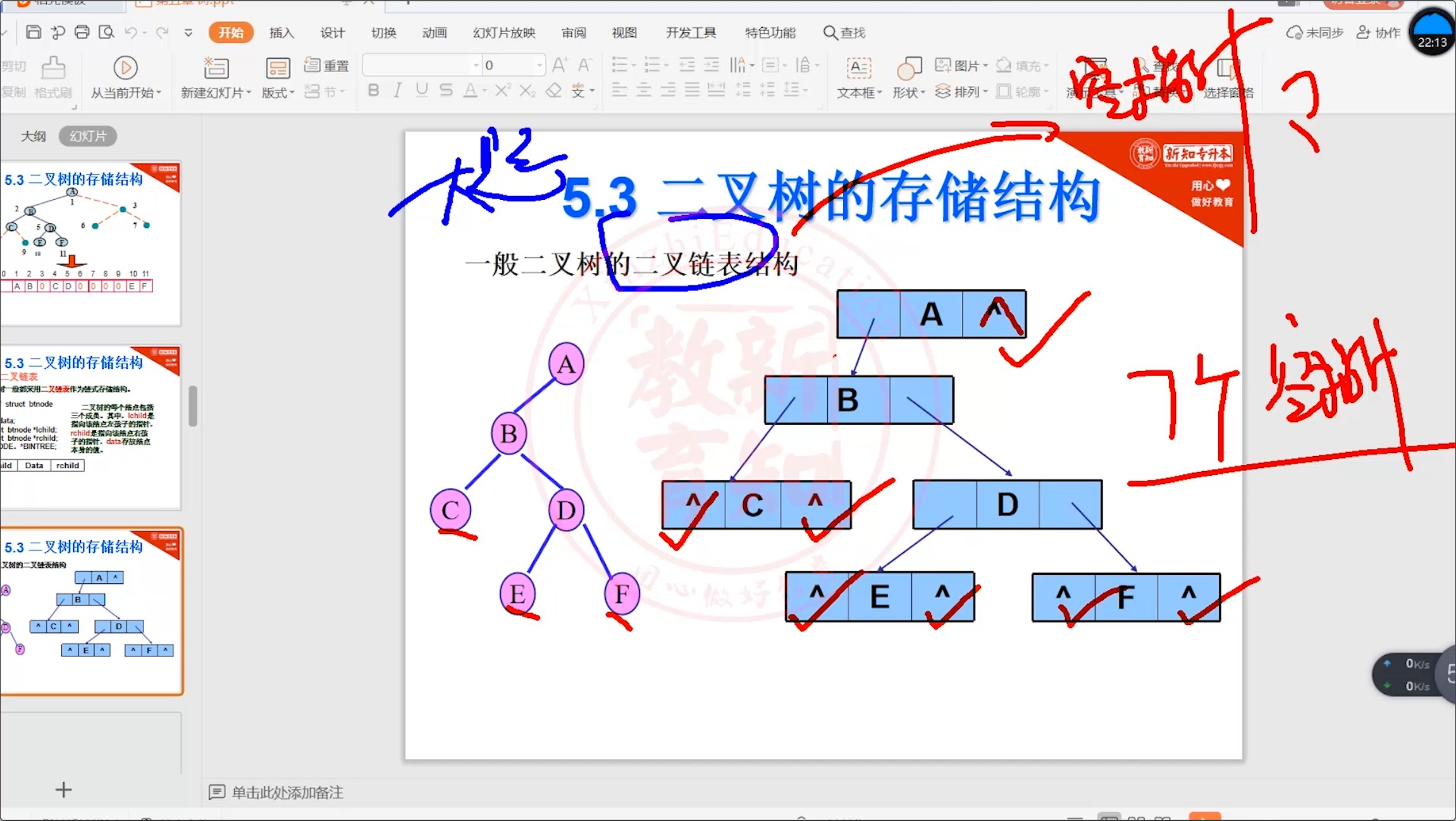
image-20220220164617939

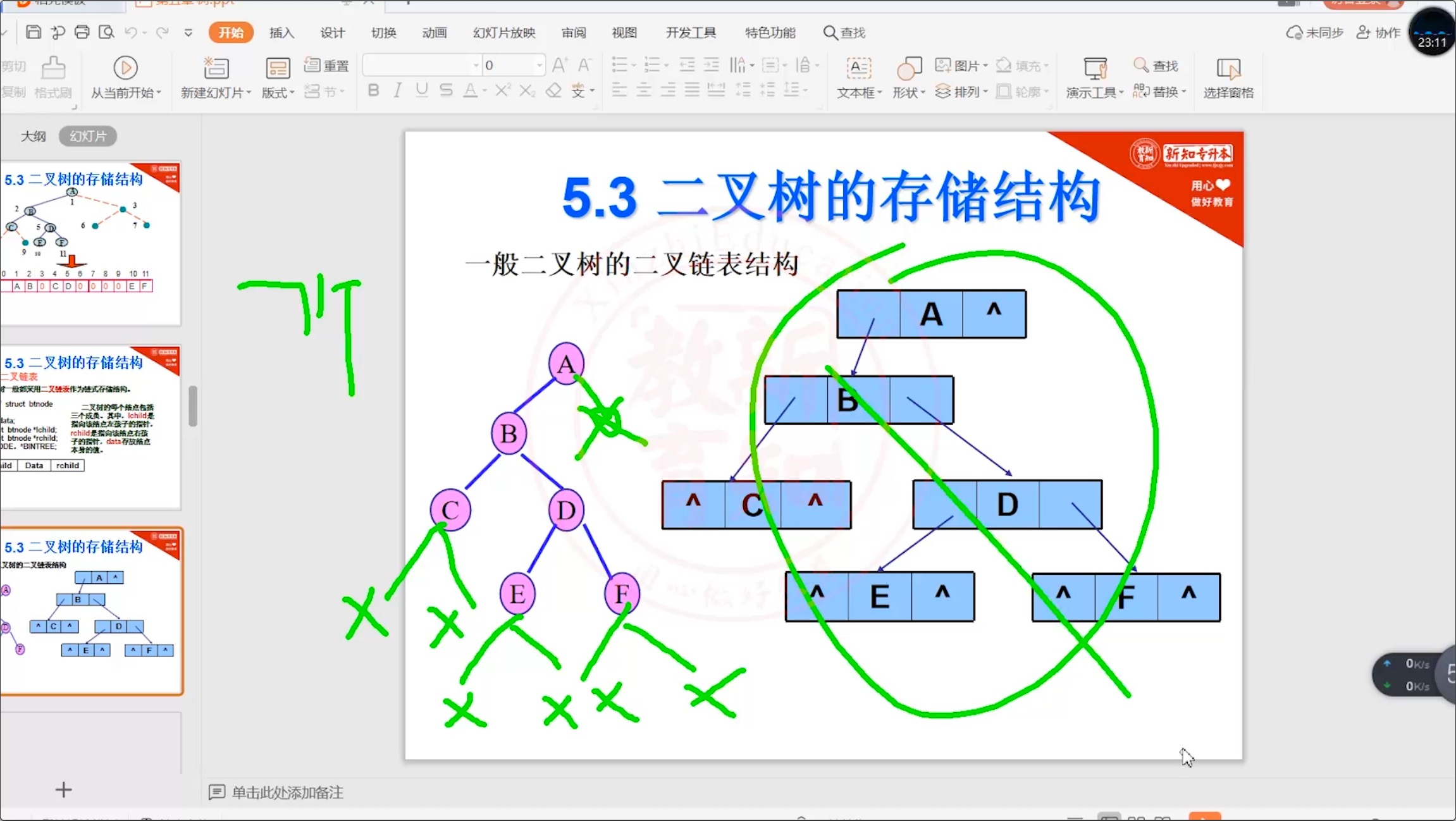
image-20220220164632502

5.4 二叉树的遍历【重要】

5.4.1 三种遍历

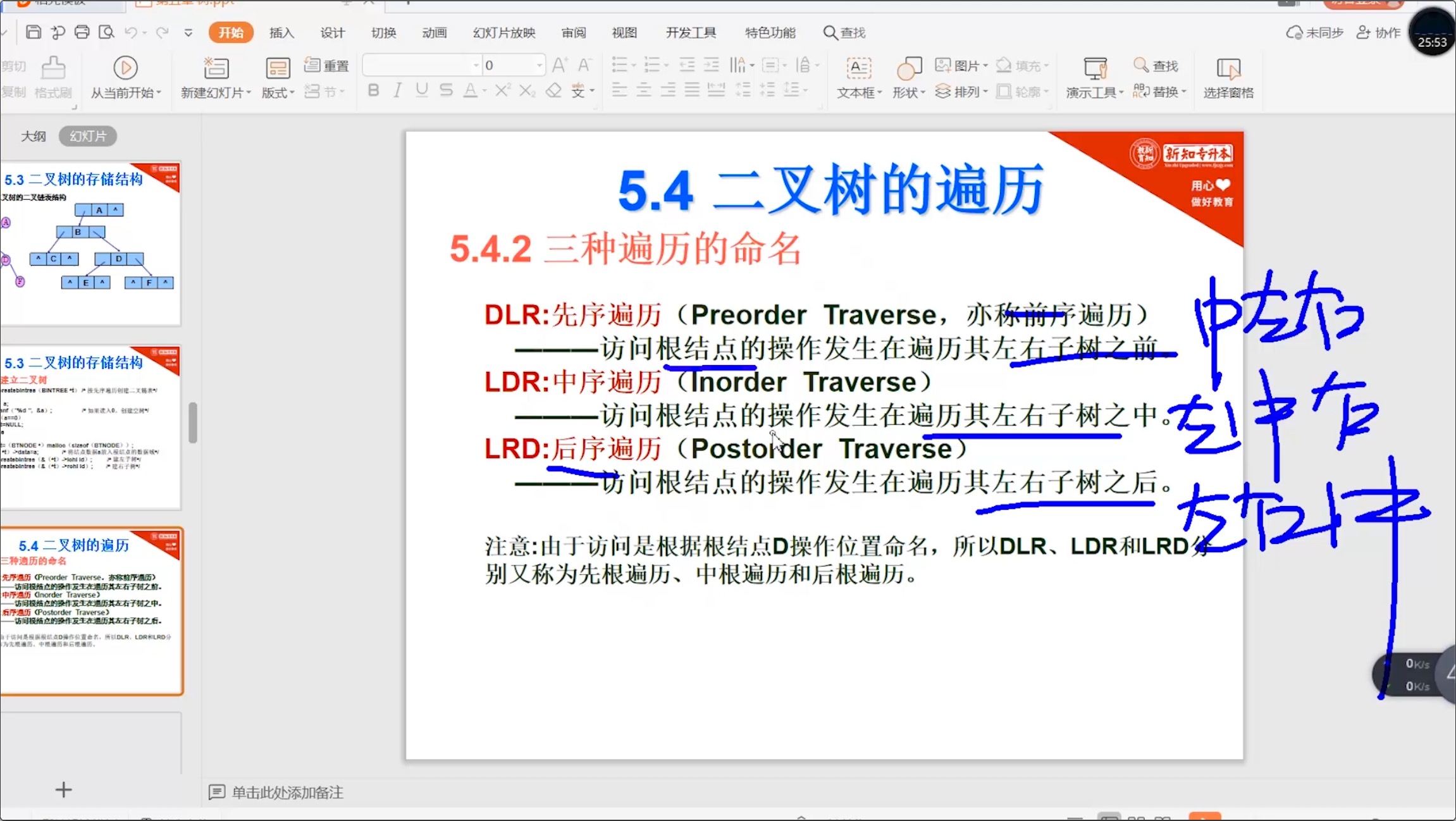
image-20220220164757178

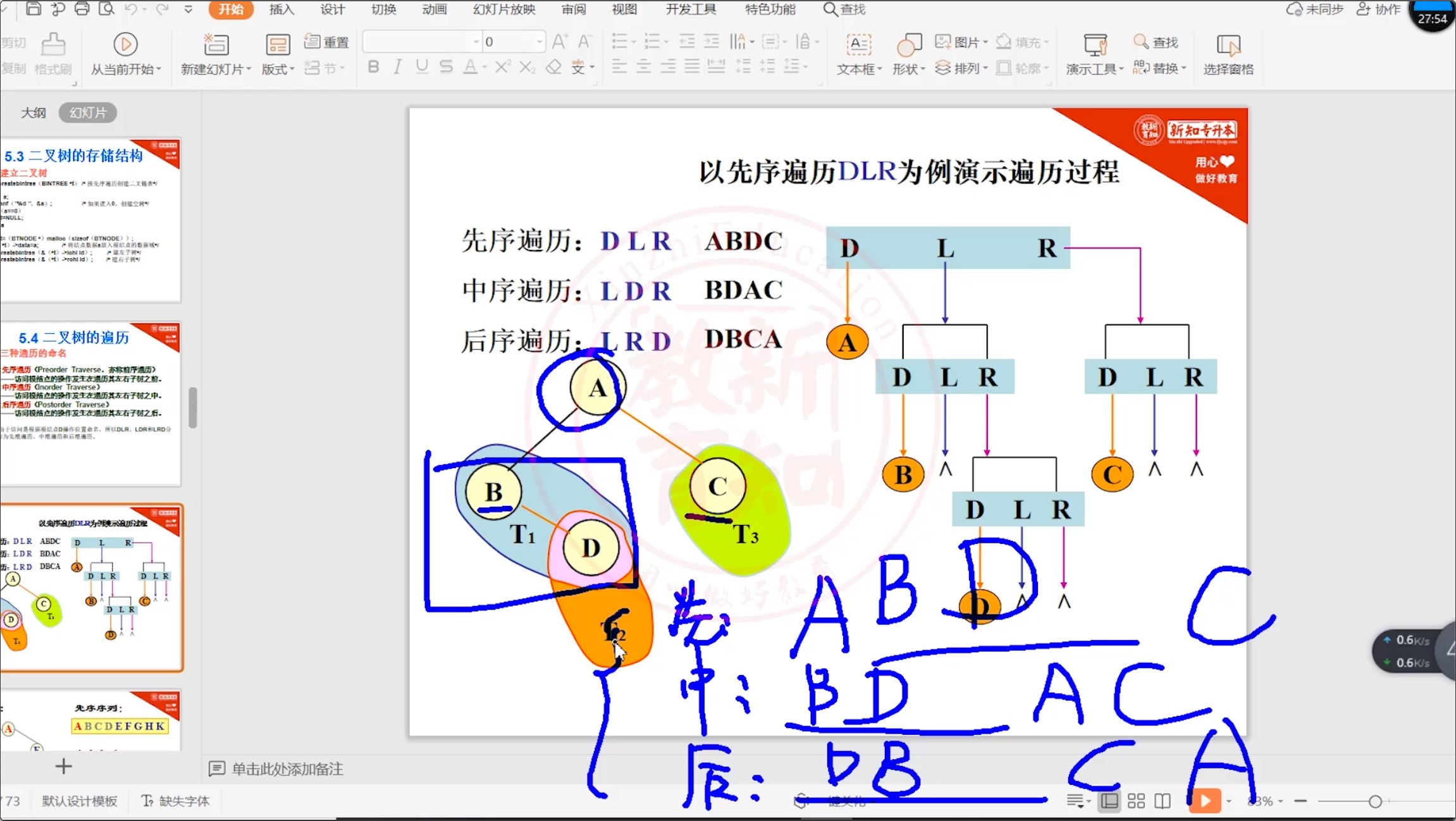
image-20220220165537180

5.4.2 三种遍历_例题

image-20220220170351174 
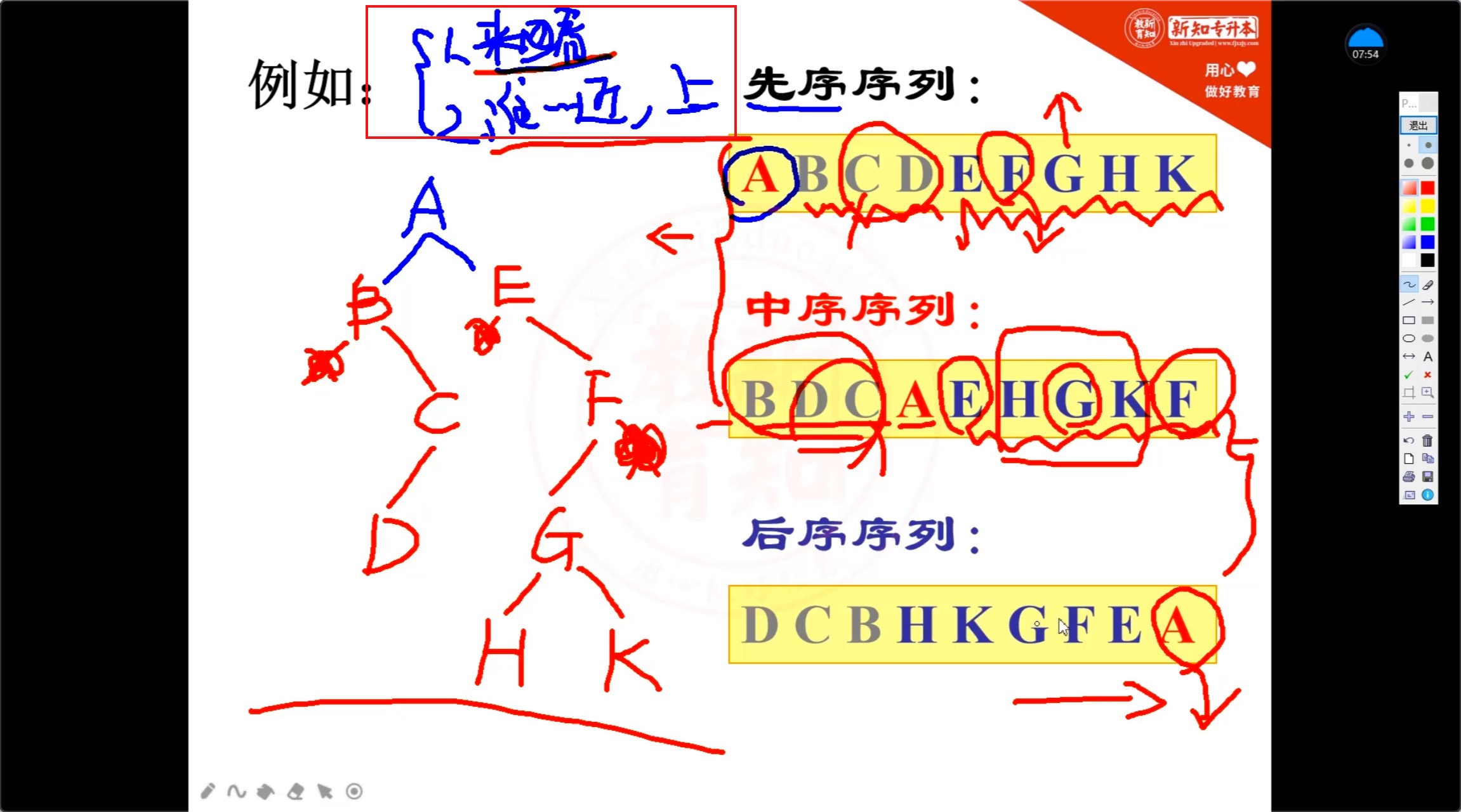
先序遍历：A(B(CD))(E(F(GHK))) -> ABCDEFGHK
中序遍历：（B(DC)）A（E((HGK)F)） -> BDCAEHGKF
后续遍历：（（DC）B）（（（HKG）F）E）A  -> DCBHKGFEA

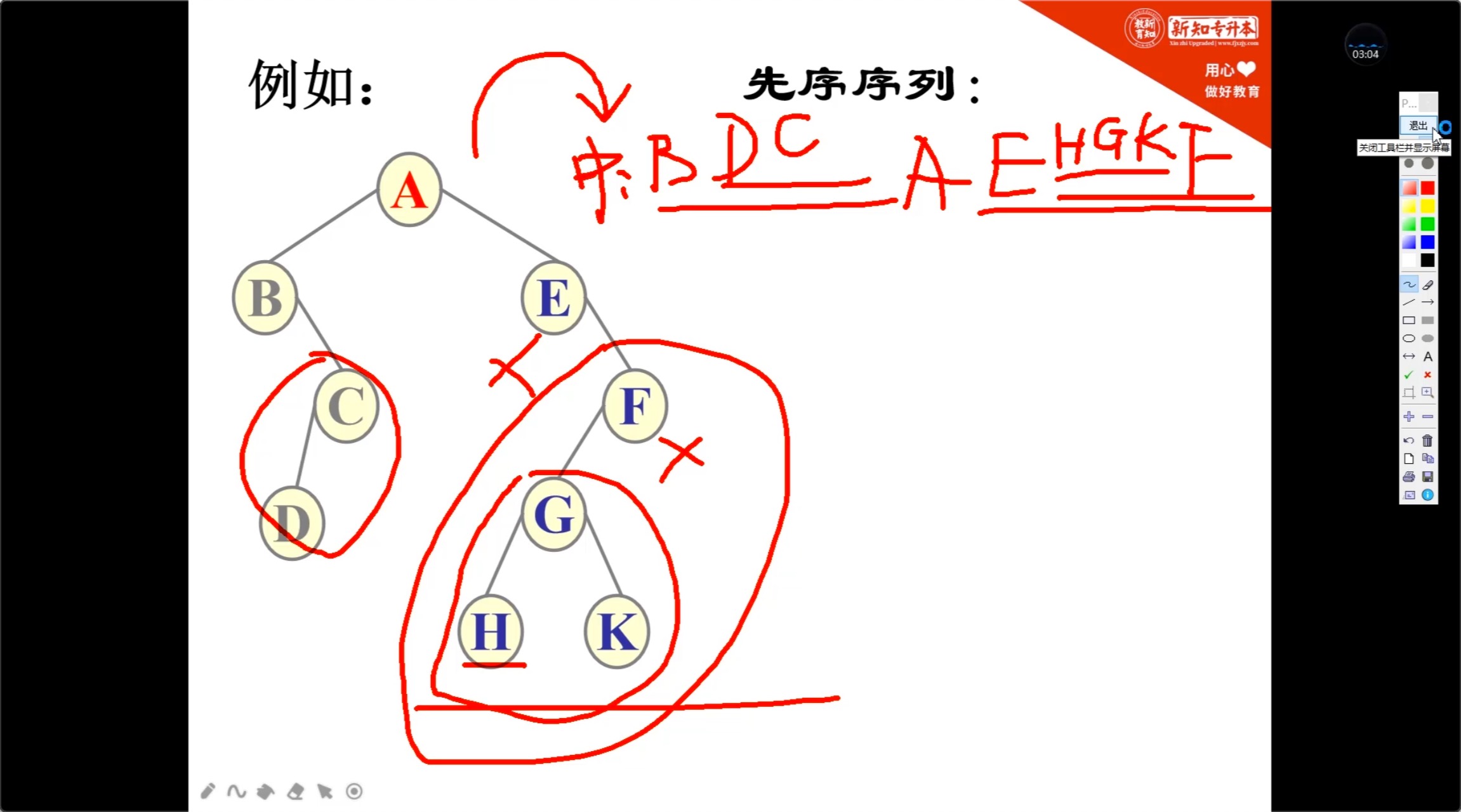
image-20220220171516604

5.4.3 根据序列来画图

image-20220220173538977

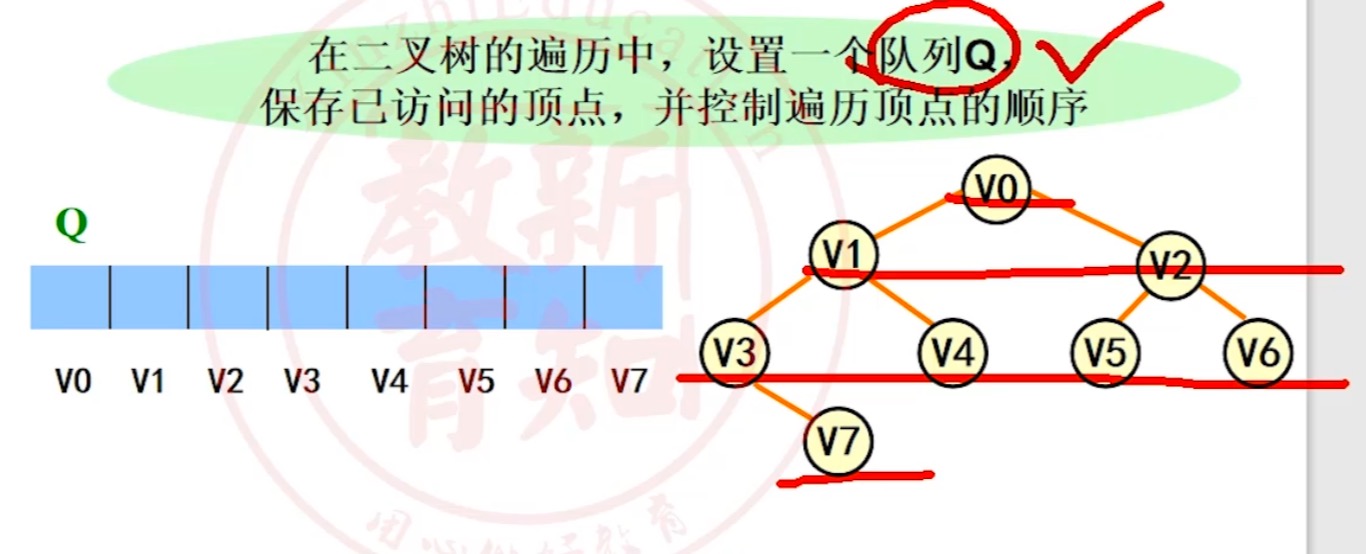
5.4.4 层次遍历

image-20220220173942627

image-20220220174013089

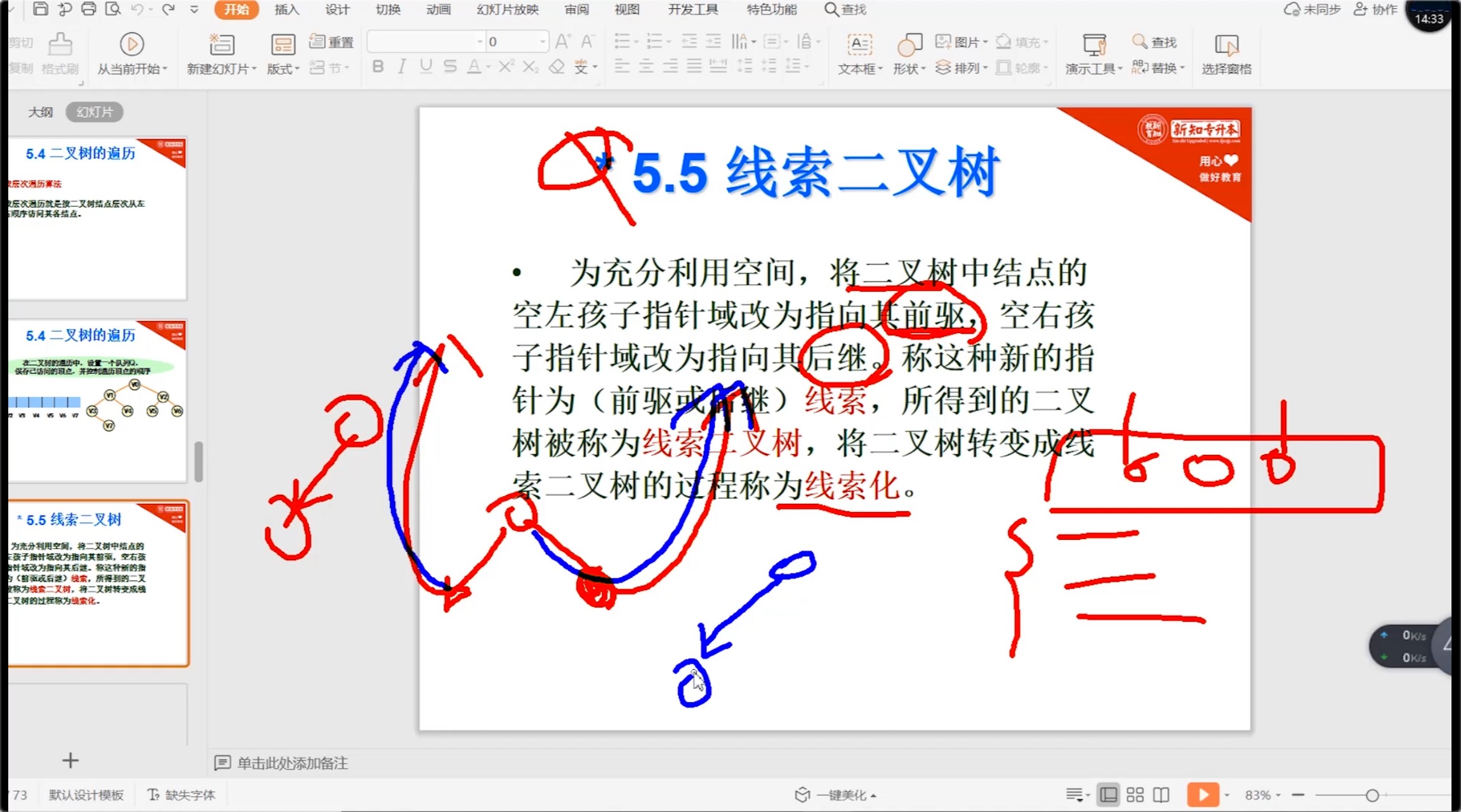
5.5 线索二叉树

image-20220220174214147

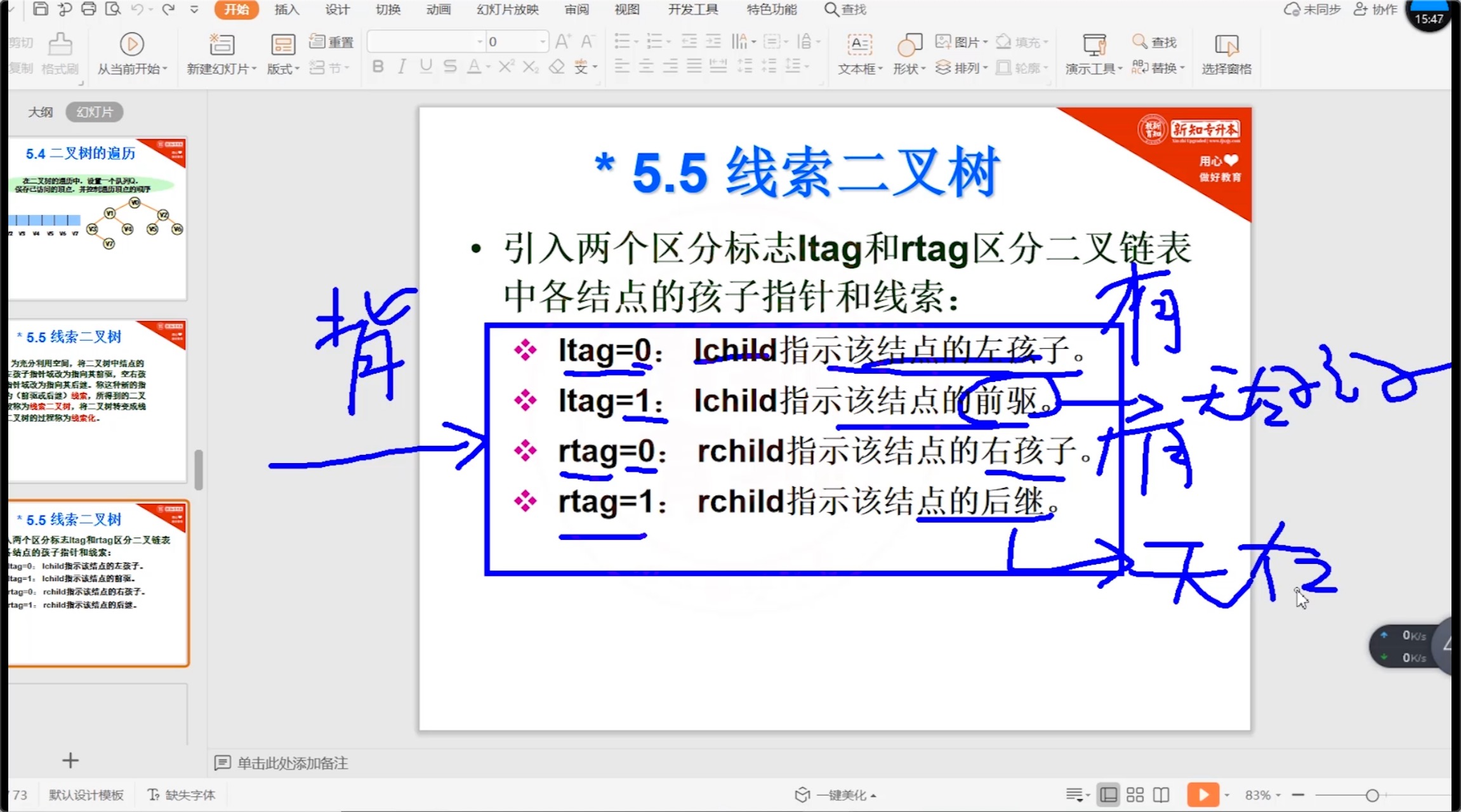
image-20220220174302173

5.6 二叉排序树【重要】

5.6.1 二叉排序树_概念和定义

image-20220220175157403

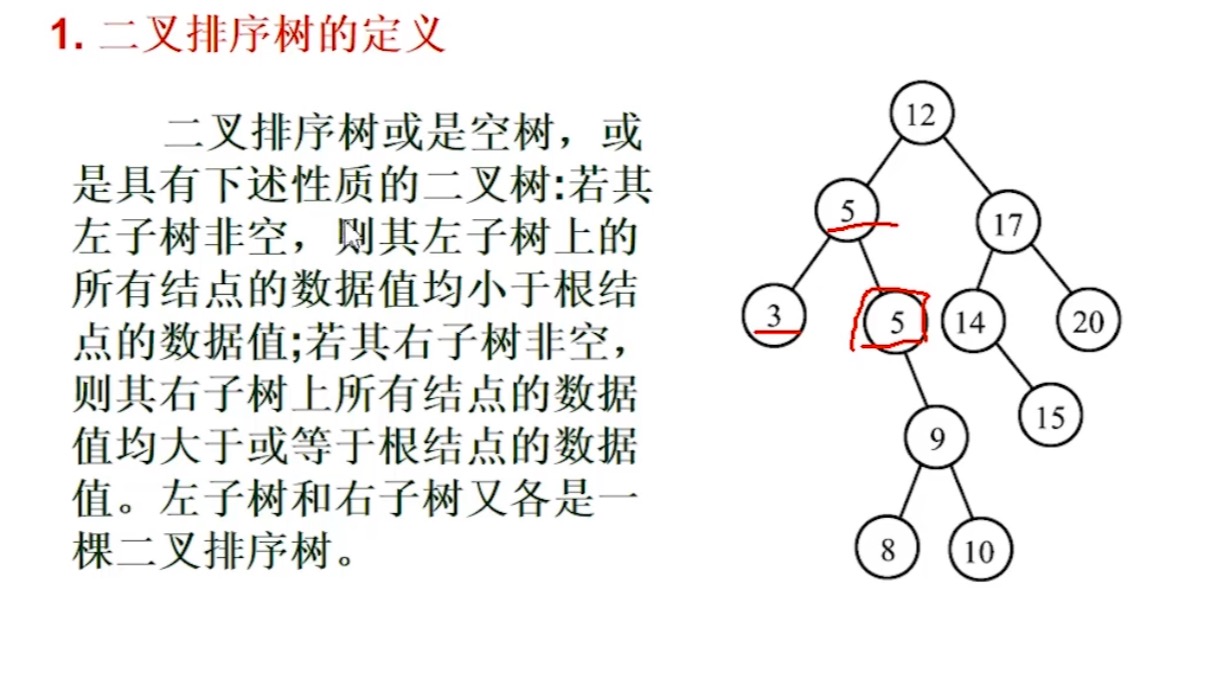
image-20220220175228432

?

image-20220220175333999

5.6.2 二叉排序树_画图

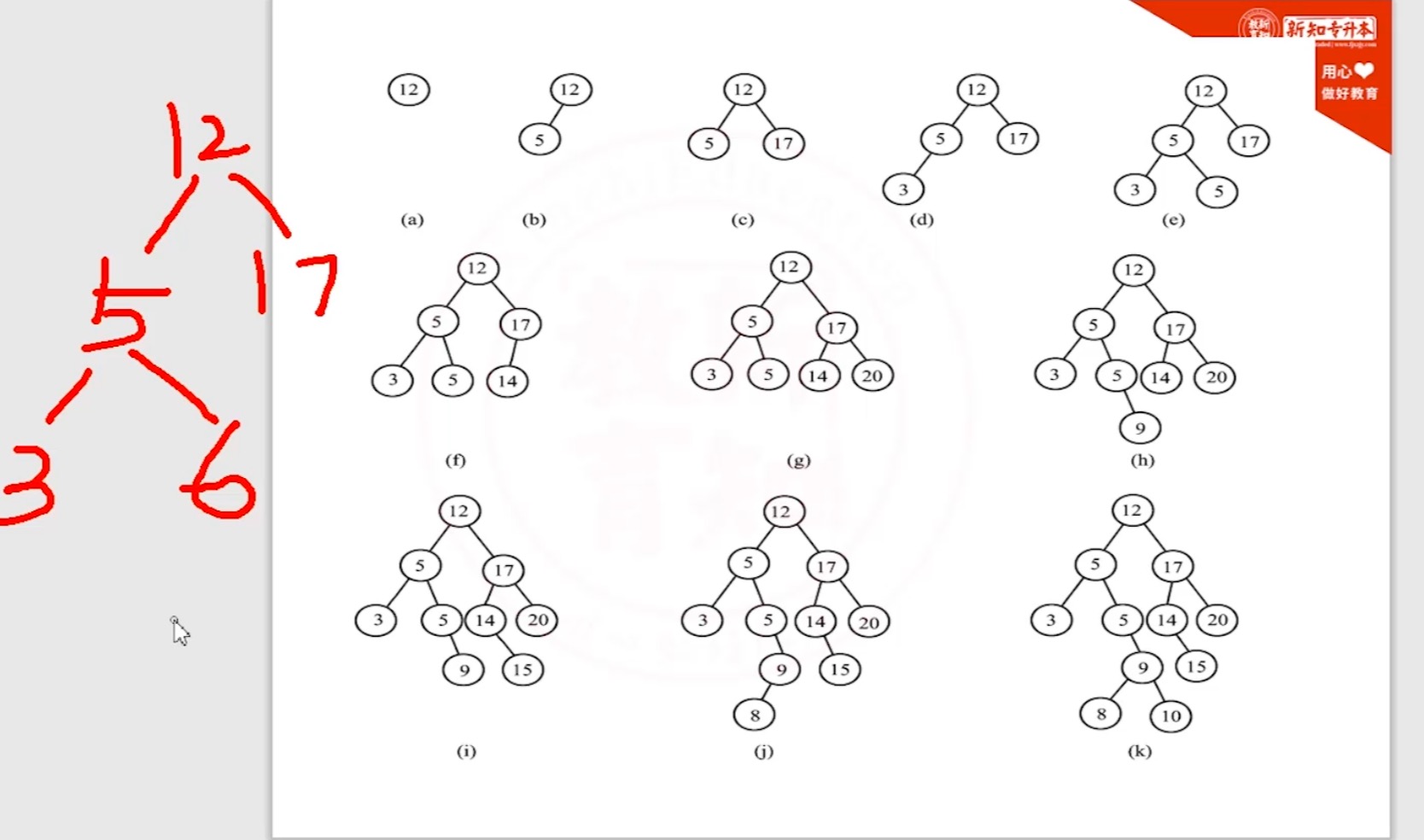
image-20220220175310785

5.7 树、森林与二叉树之间的转换

5.7.1 三叉树 -> 二叉树

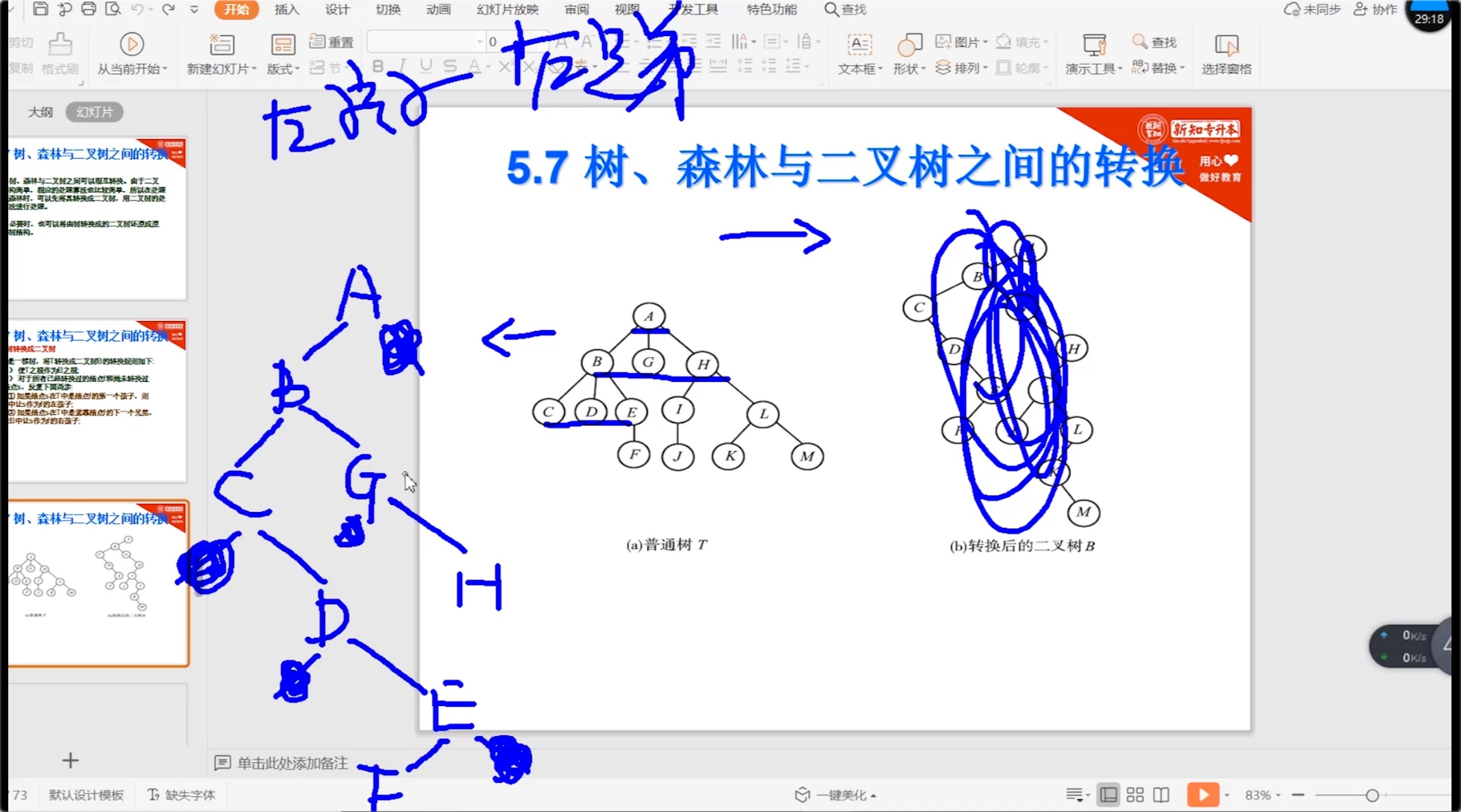
image-20220220175633019

5.7.2 二叉树 -> 三叉树

image-20220220180750394

5.7.3 森林 -> 二叉树

image-20220220192039980

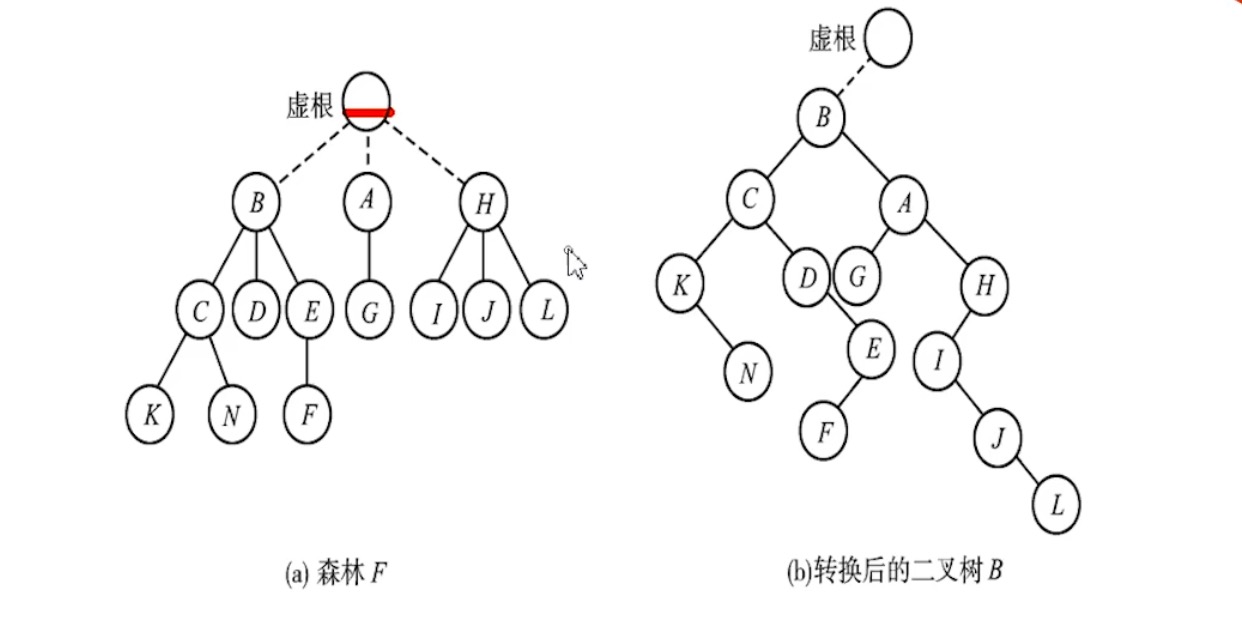
image-20220220192100533

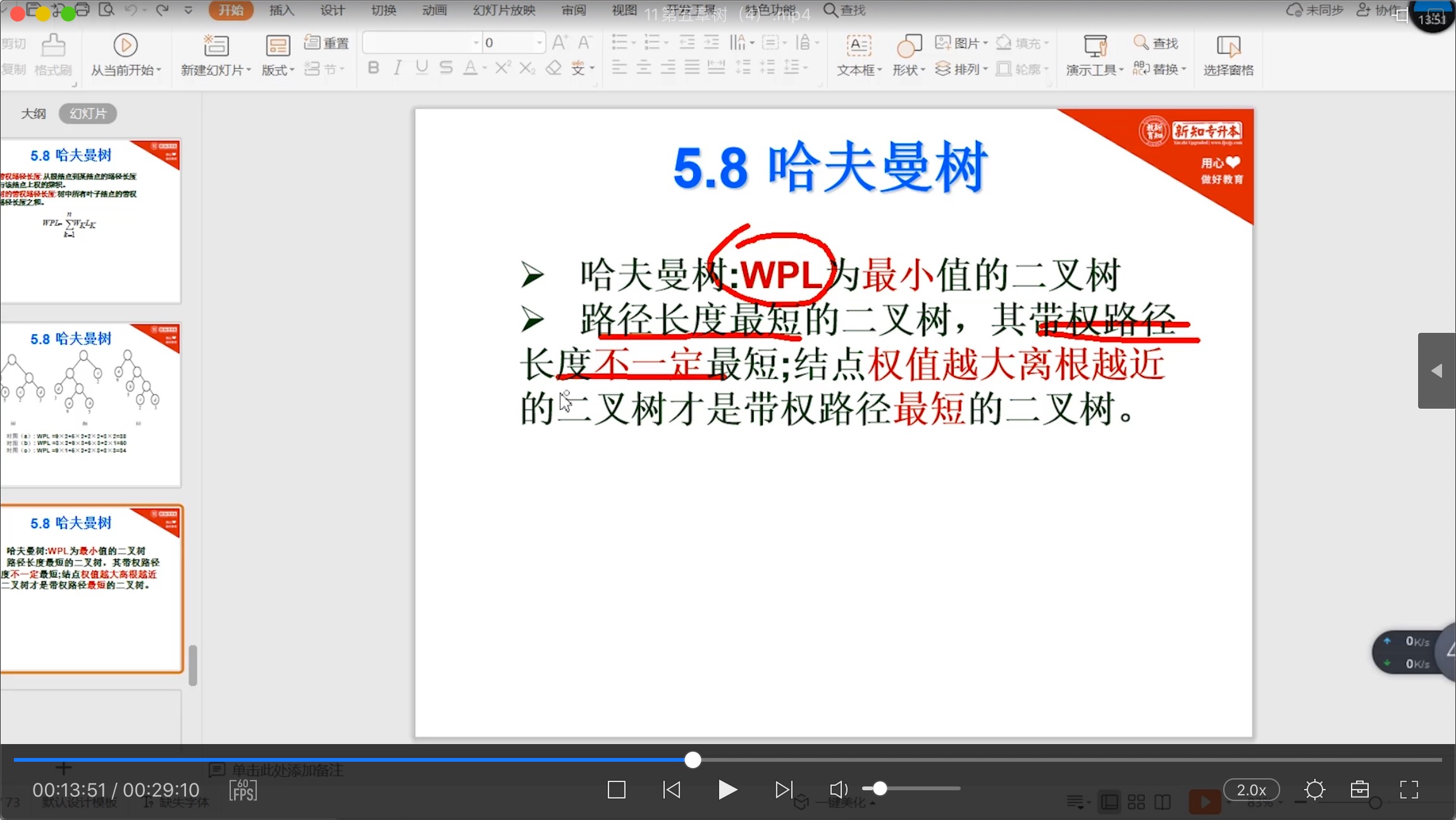
5.8 哈夫曼树

5.8.1 哈夫曼树_概念

image-20220220193645487

image-20220220194236398

5.8.2 哈夫曼树_带权路径之和

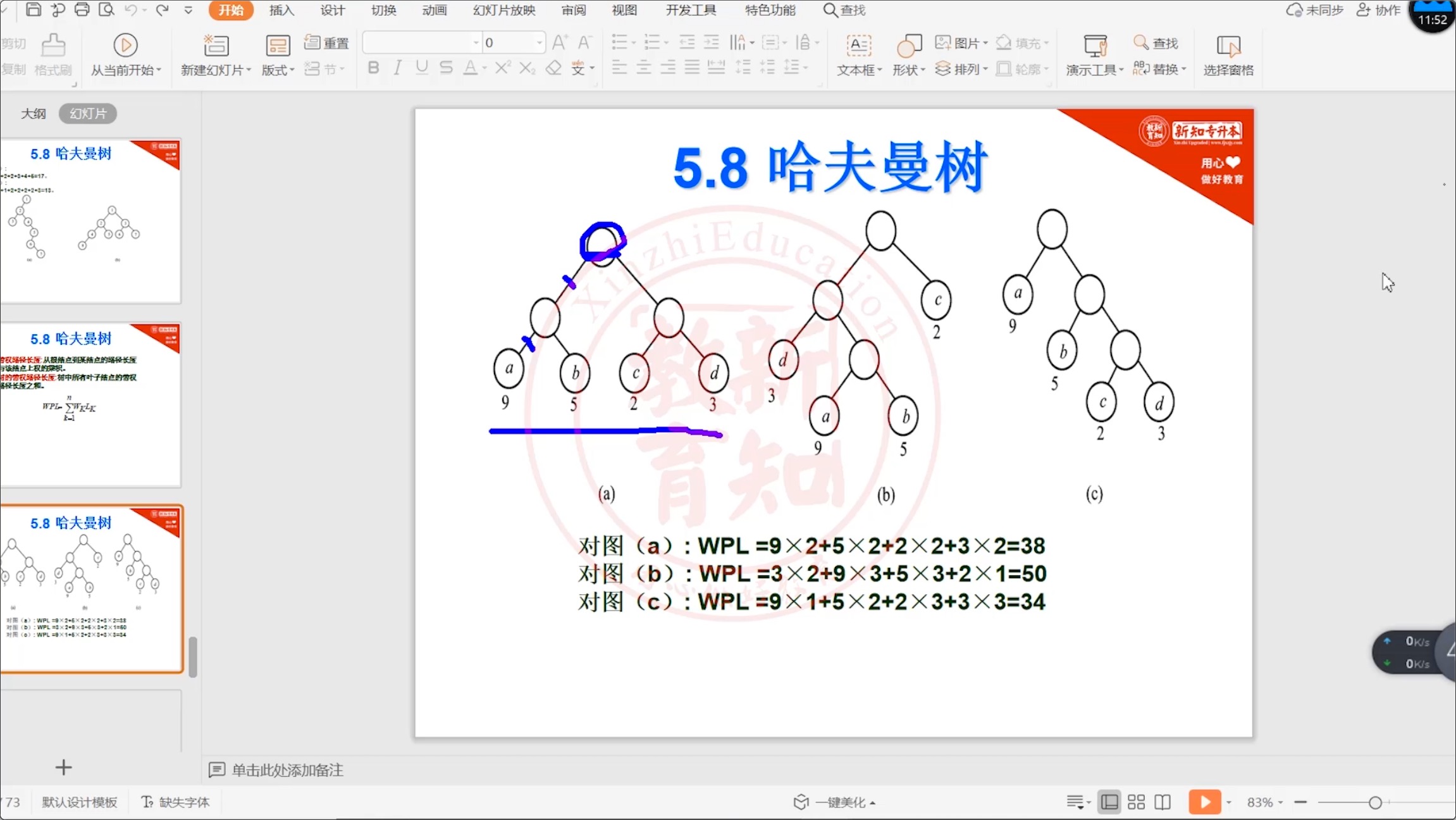
image-20220220194339042

?

image-20220220194411717

5.8.3 哈夫曼树_画图

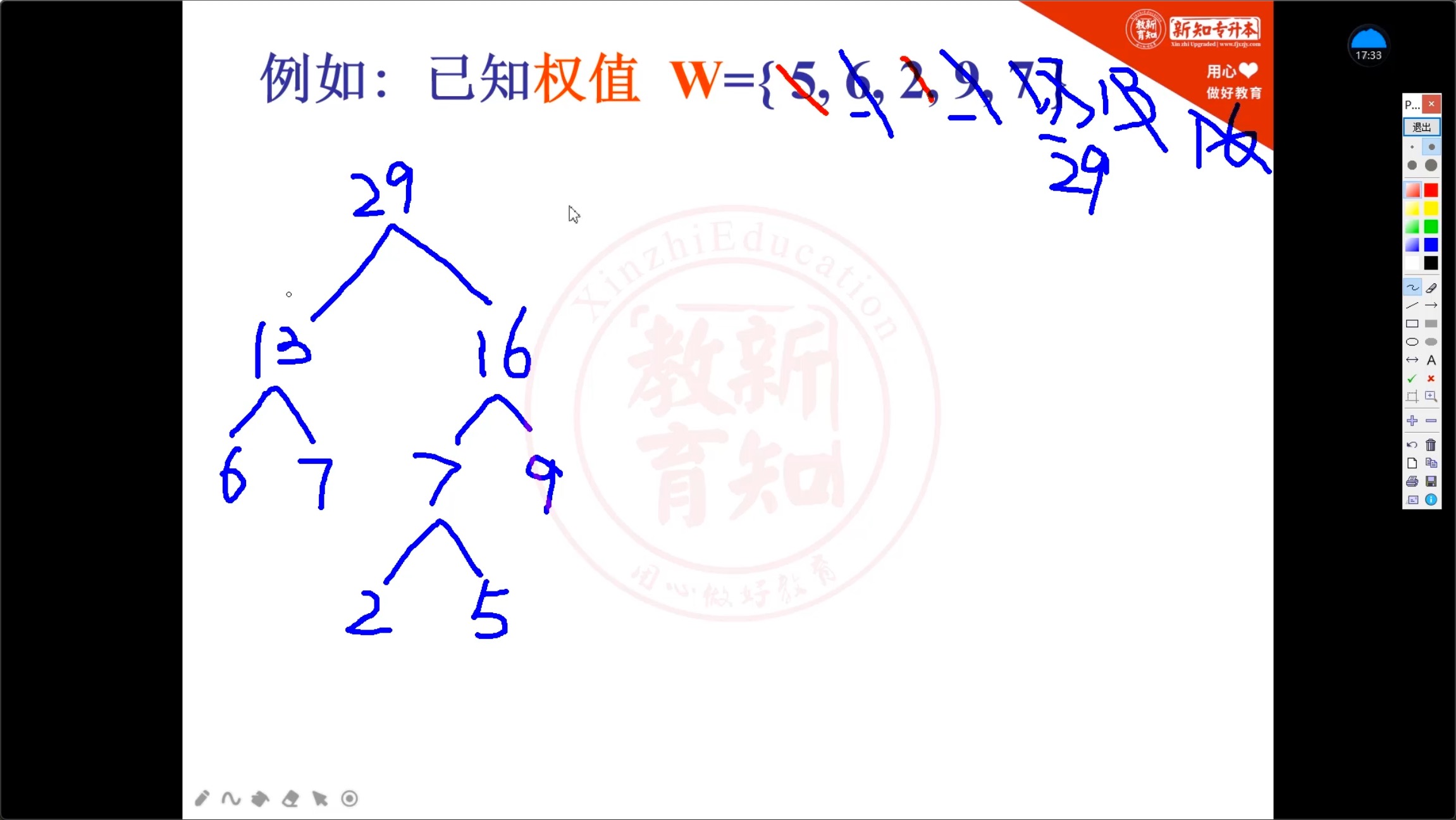
image-20220220194821200

5.8.4 哈夫曼树_例题

  • 题目：一个哈夫曼树有10个权值，那么该哈夫曼树总共有多少个结点

    10个权值 = 10个叶子结点 = 10个0为0的结点
n0 = n2 + 1
10 = n2 + 1
n2 = 10 - 1 = 9
一共的结点 = n0 + n2 = 19个

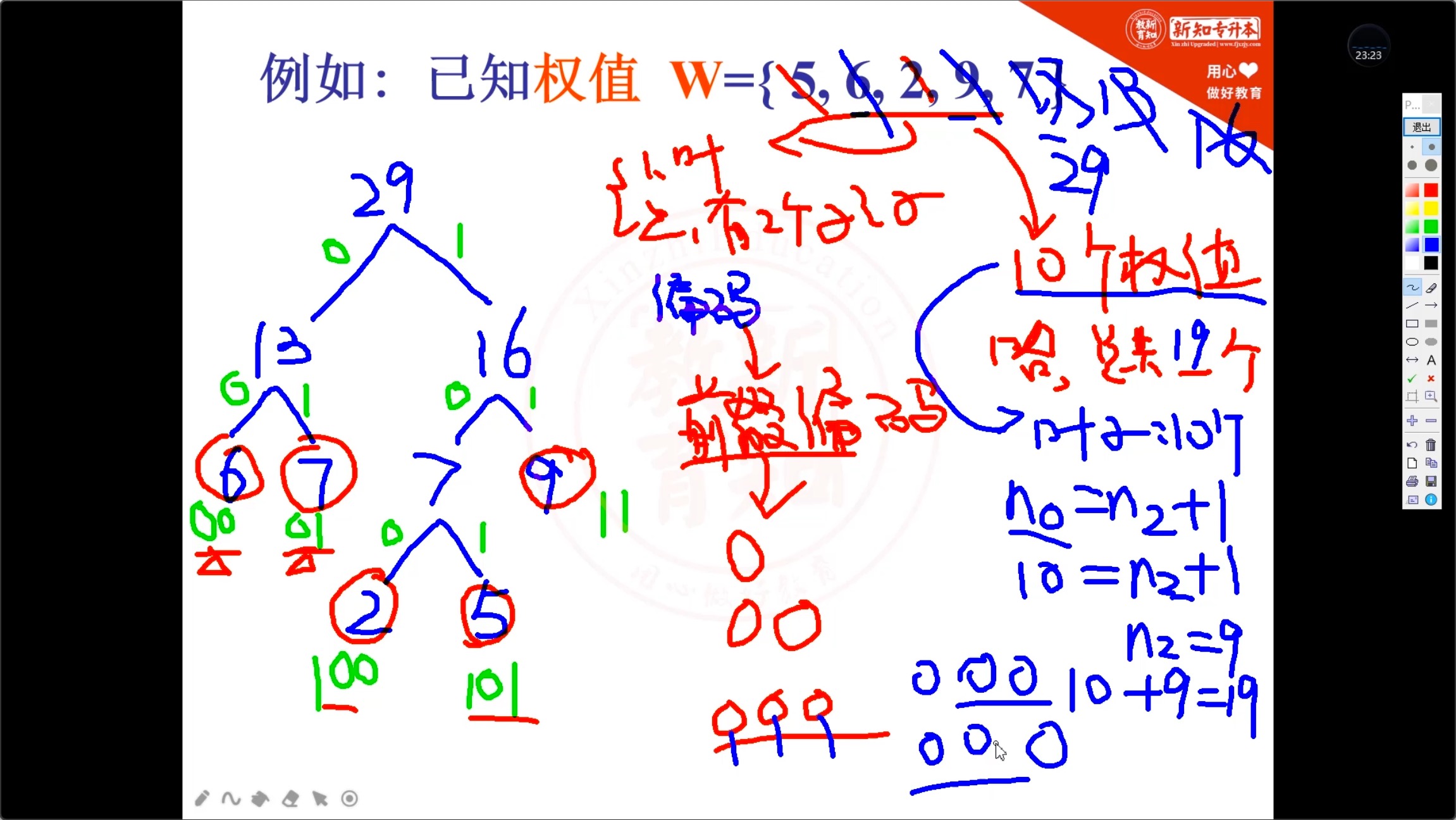
image-20220220195210642

5.8.5 哈夫曼树_电文题

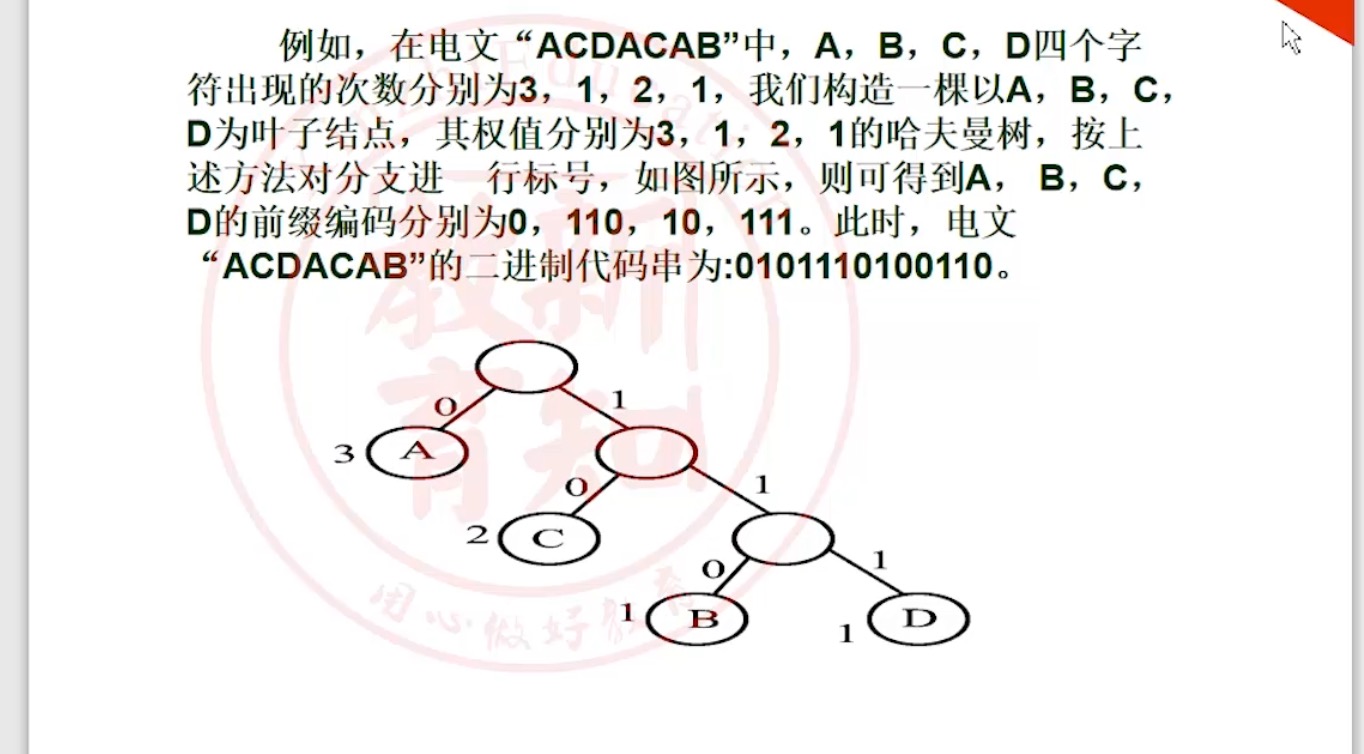
image-20220220201641571

第 6 章 - 图

6.1 图的基本概念

6.1.1 图的定义

image-20220221132718972

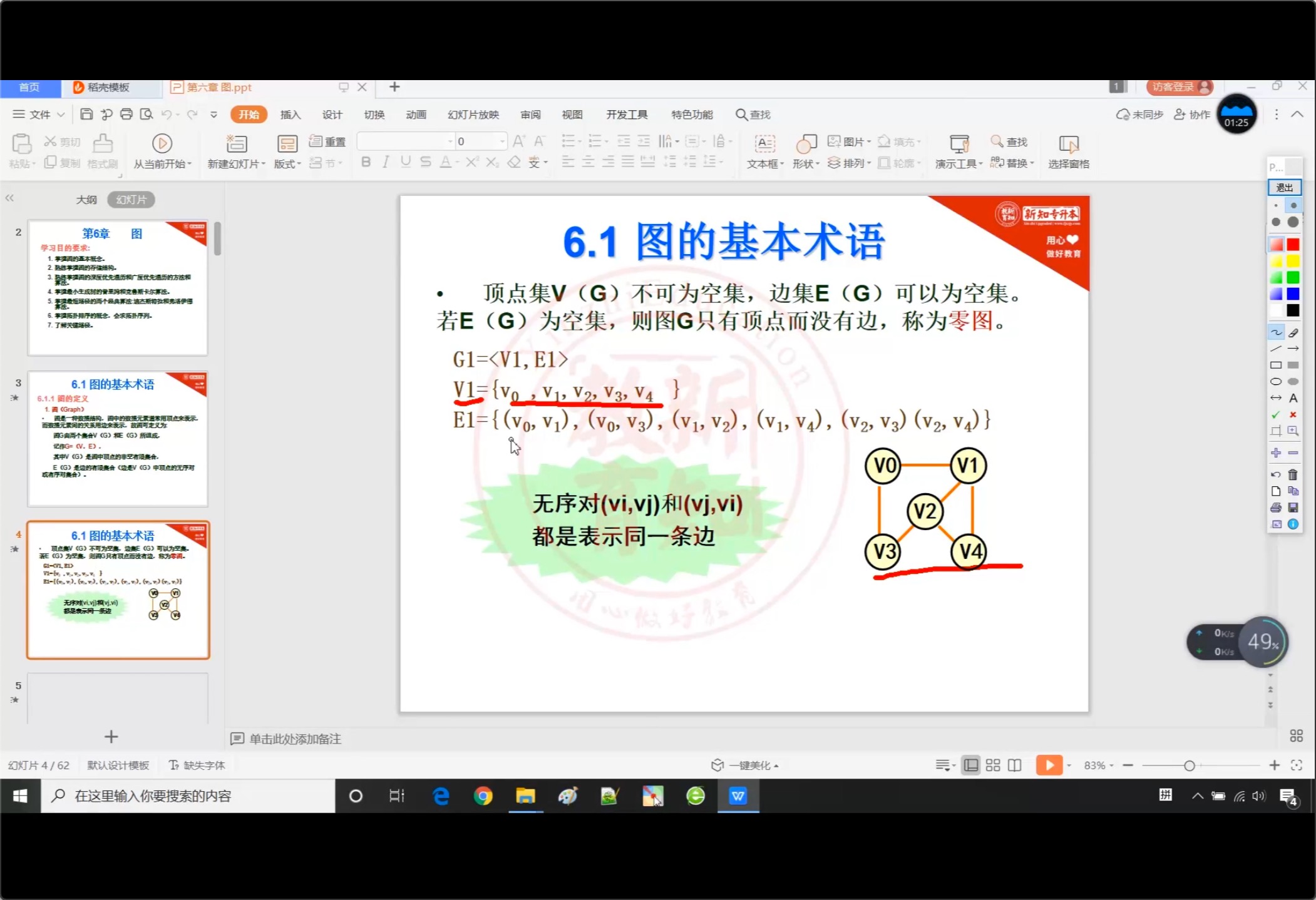
image-20220221132738367

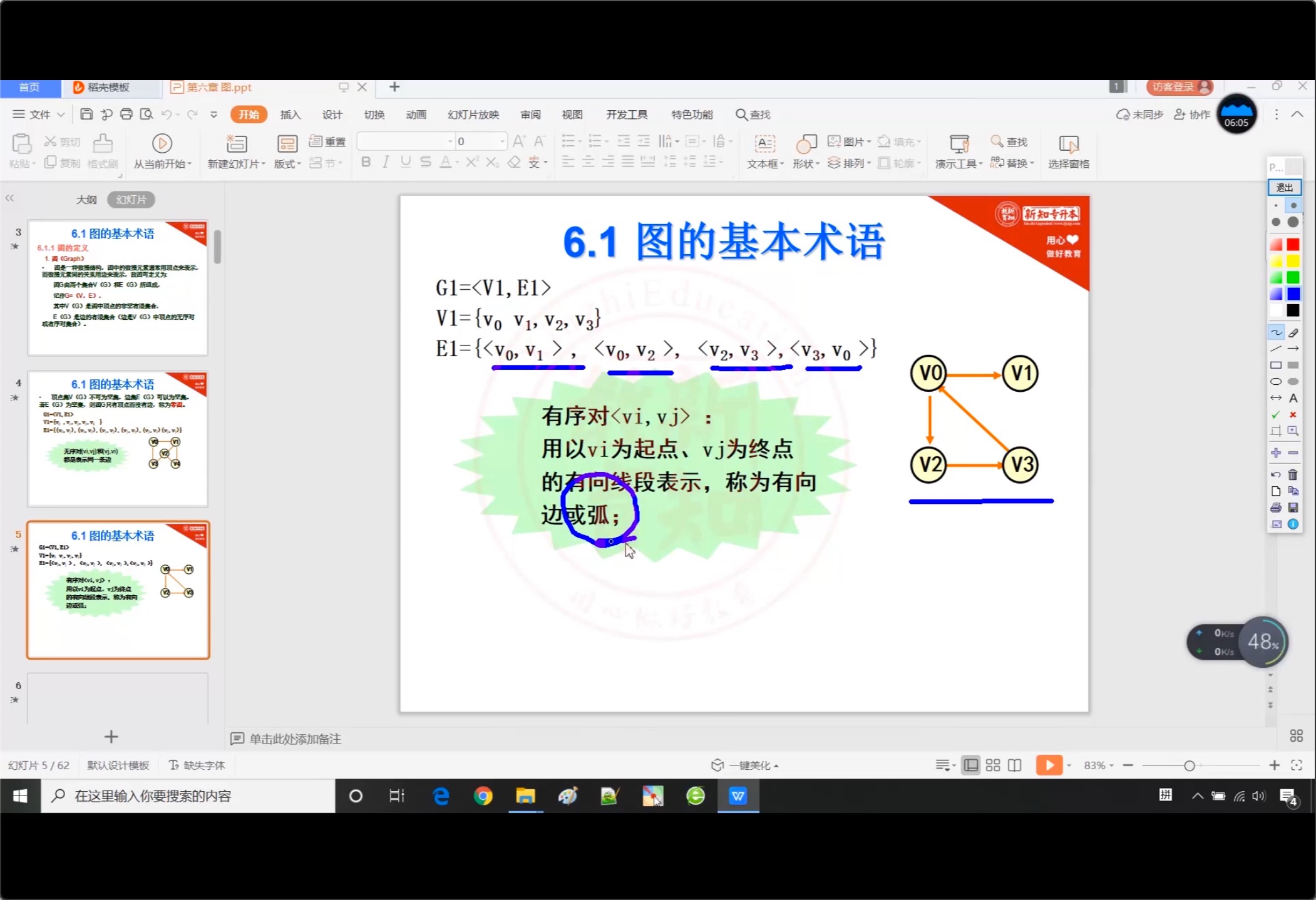
image-20220221132831289

image-20220221132949002

6.1.2 完全图

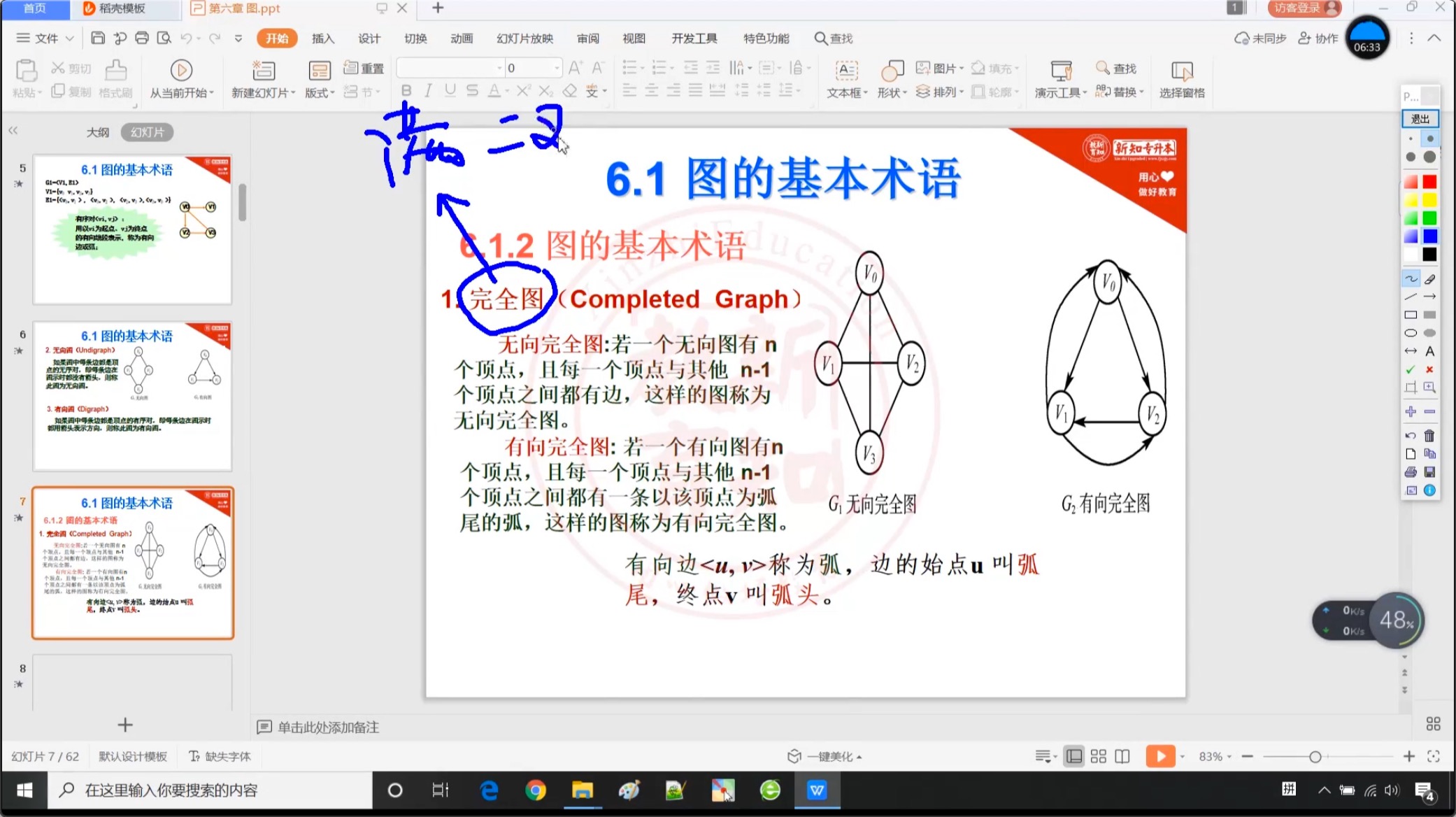
image-20220221133258878

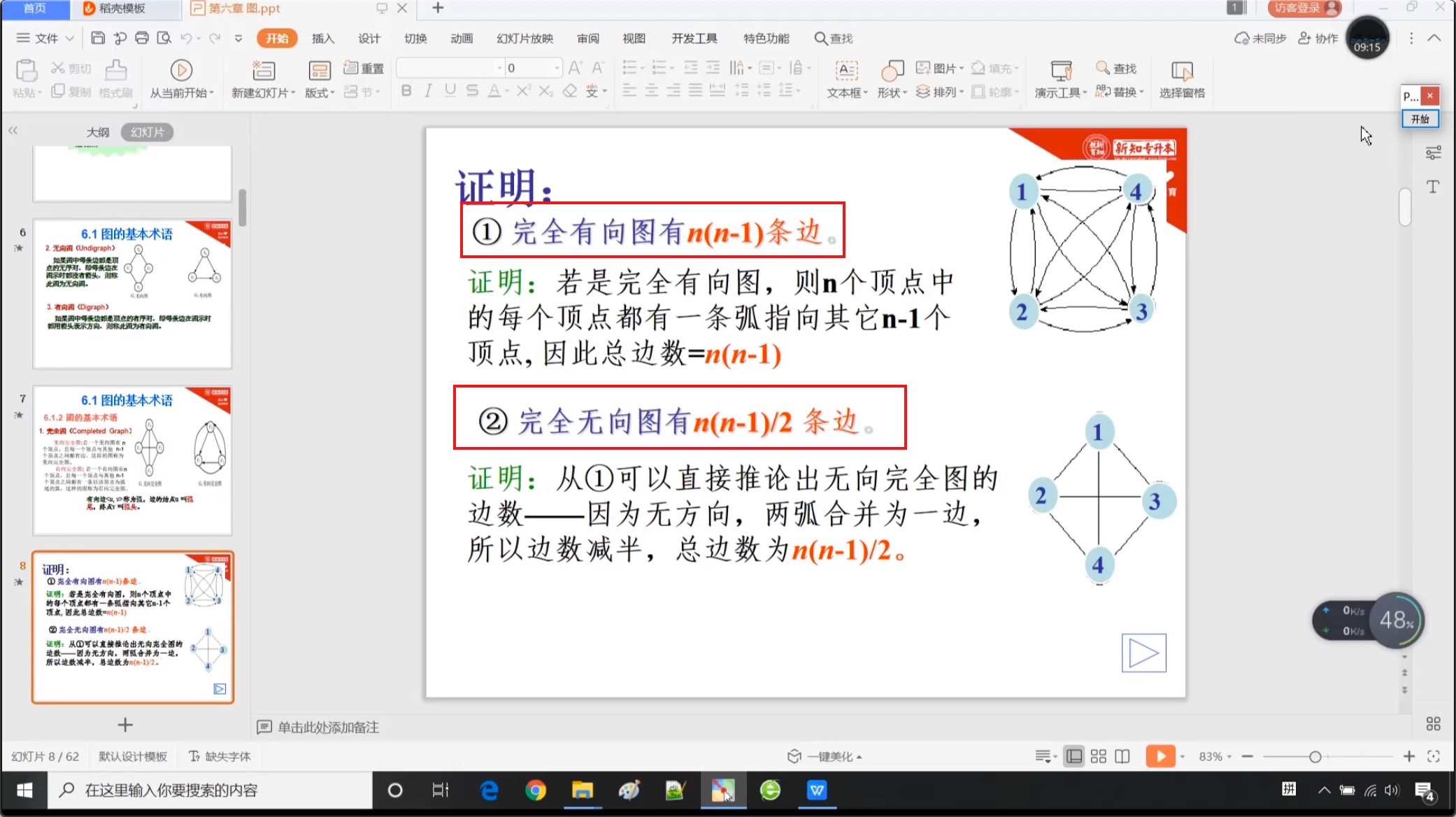
image-20220221133342472

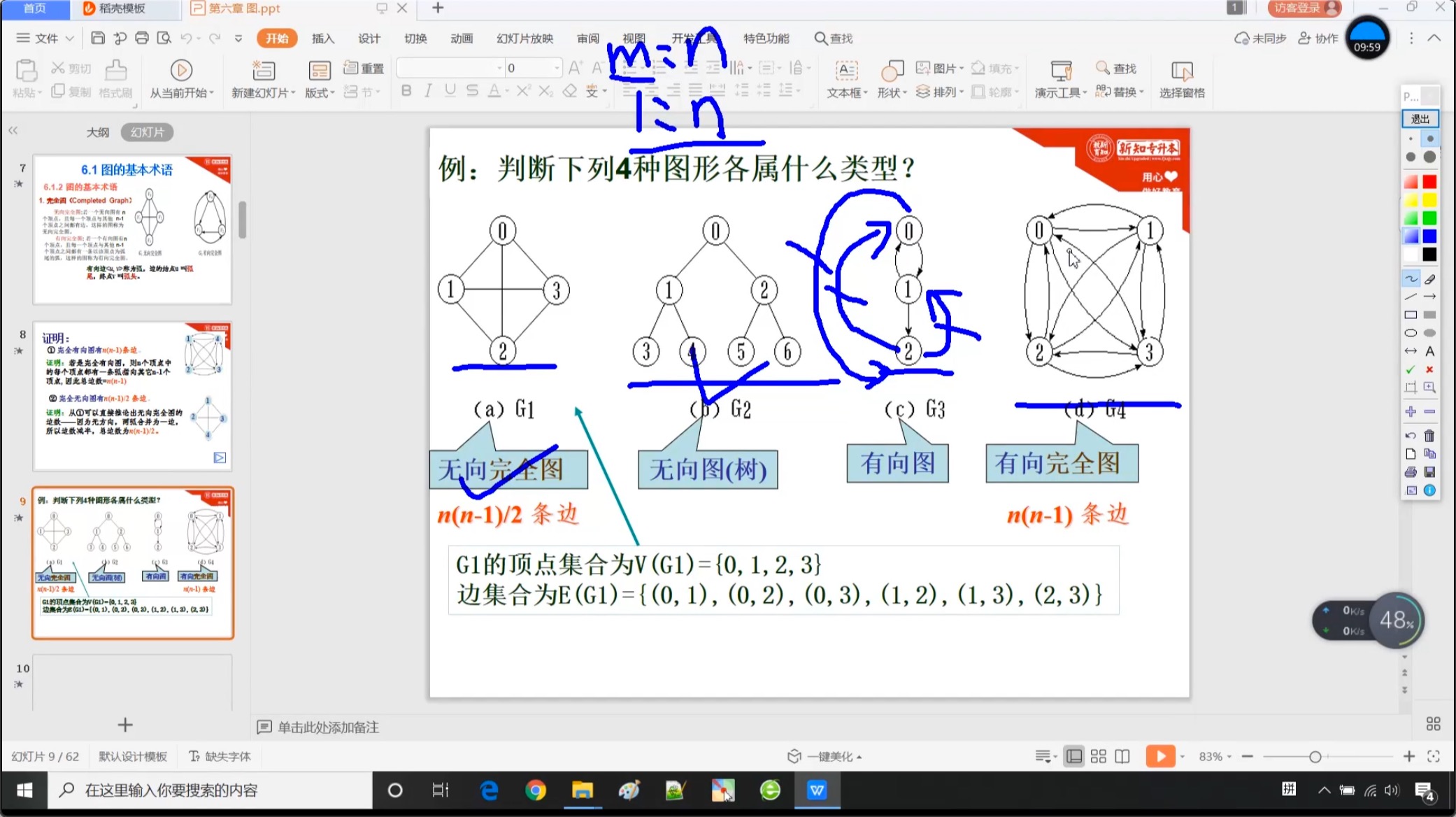
image-20220221133423765

6.1.3 子图

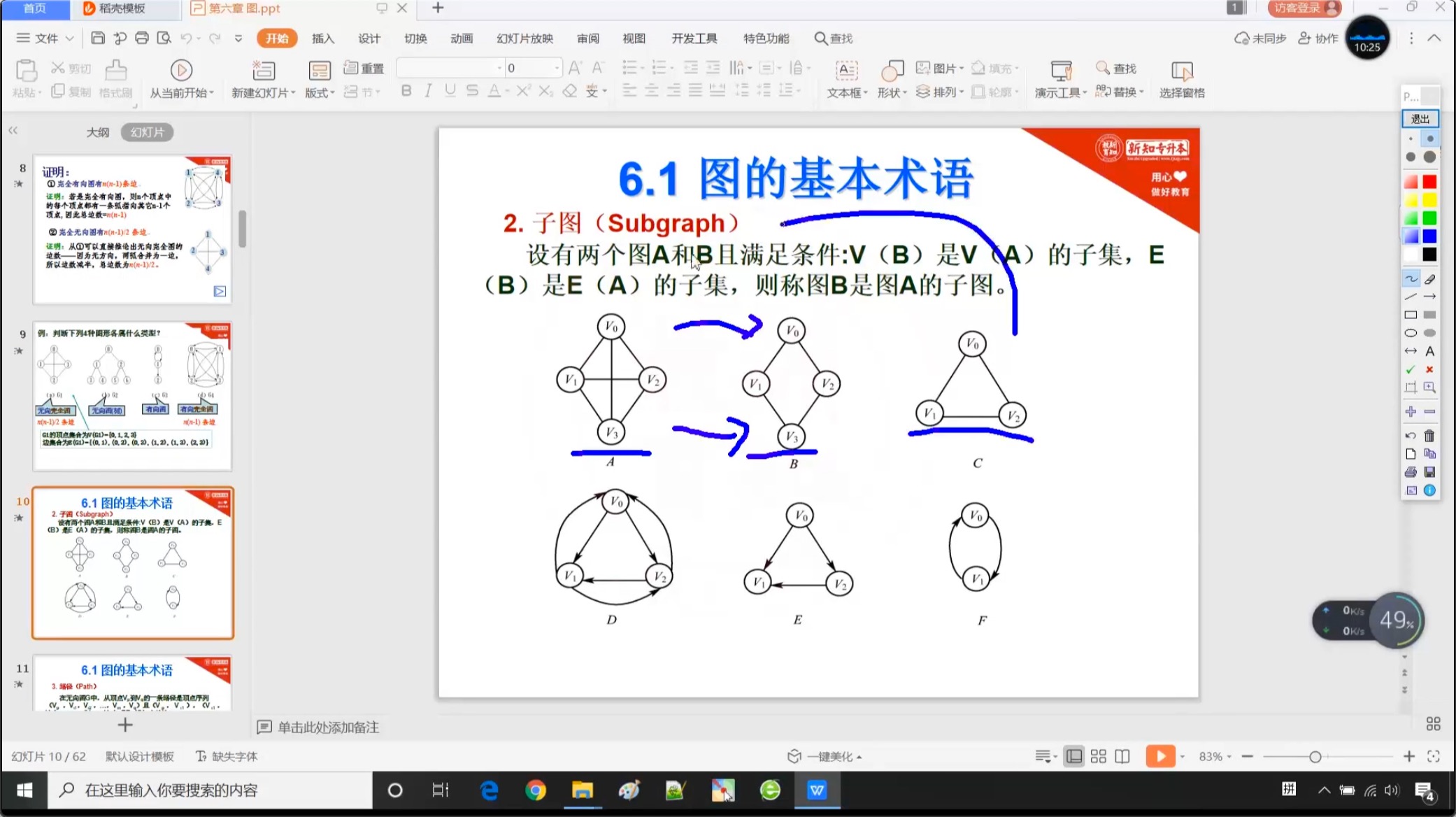
image-20220221133538622

6.1.4 路径

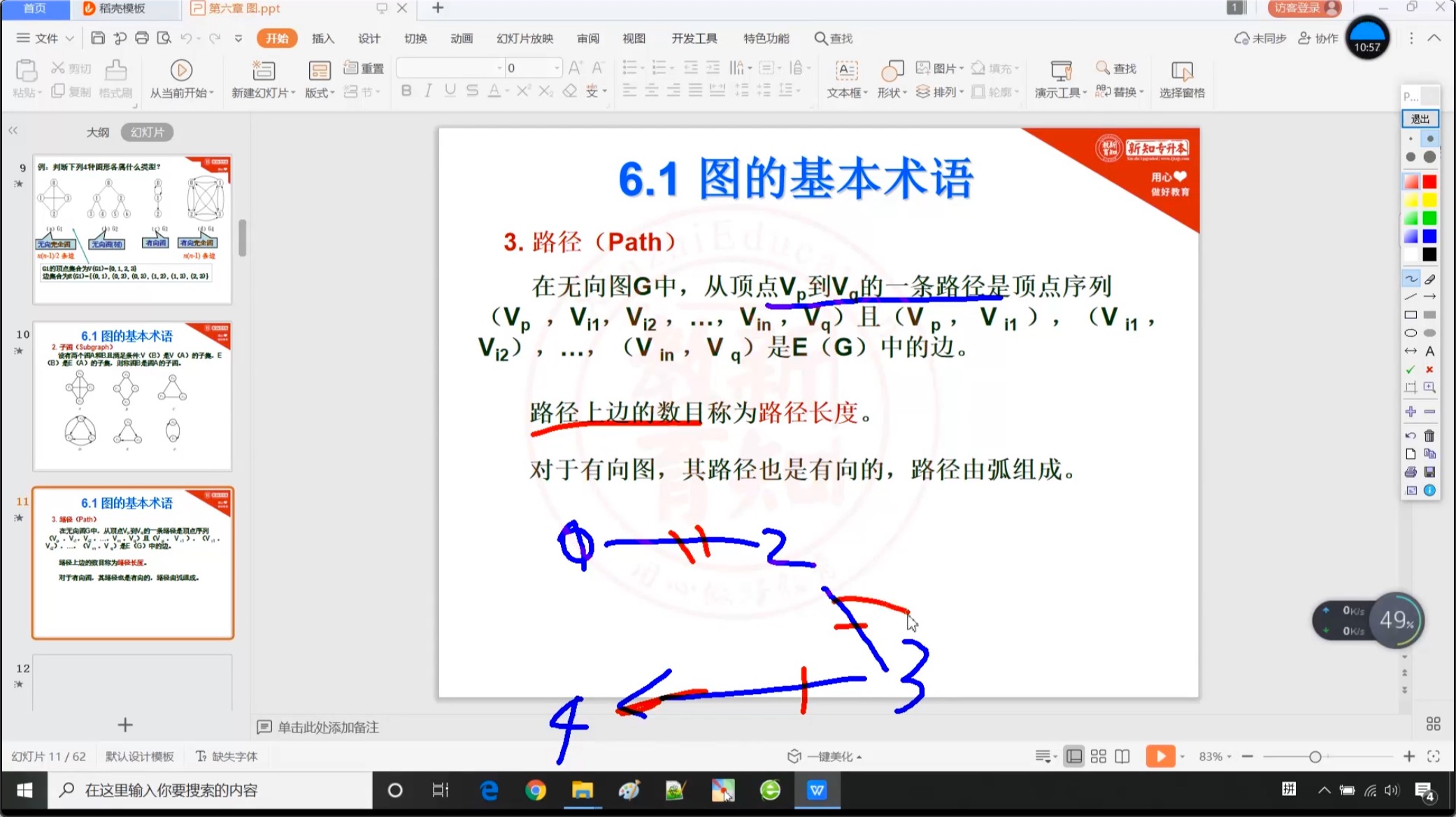
image-20220221133621473

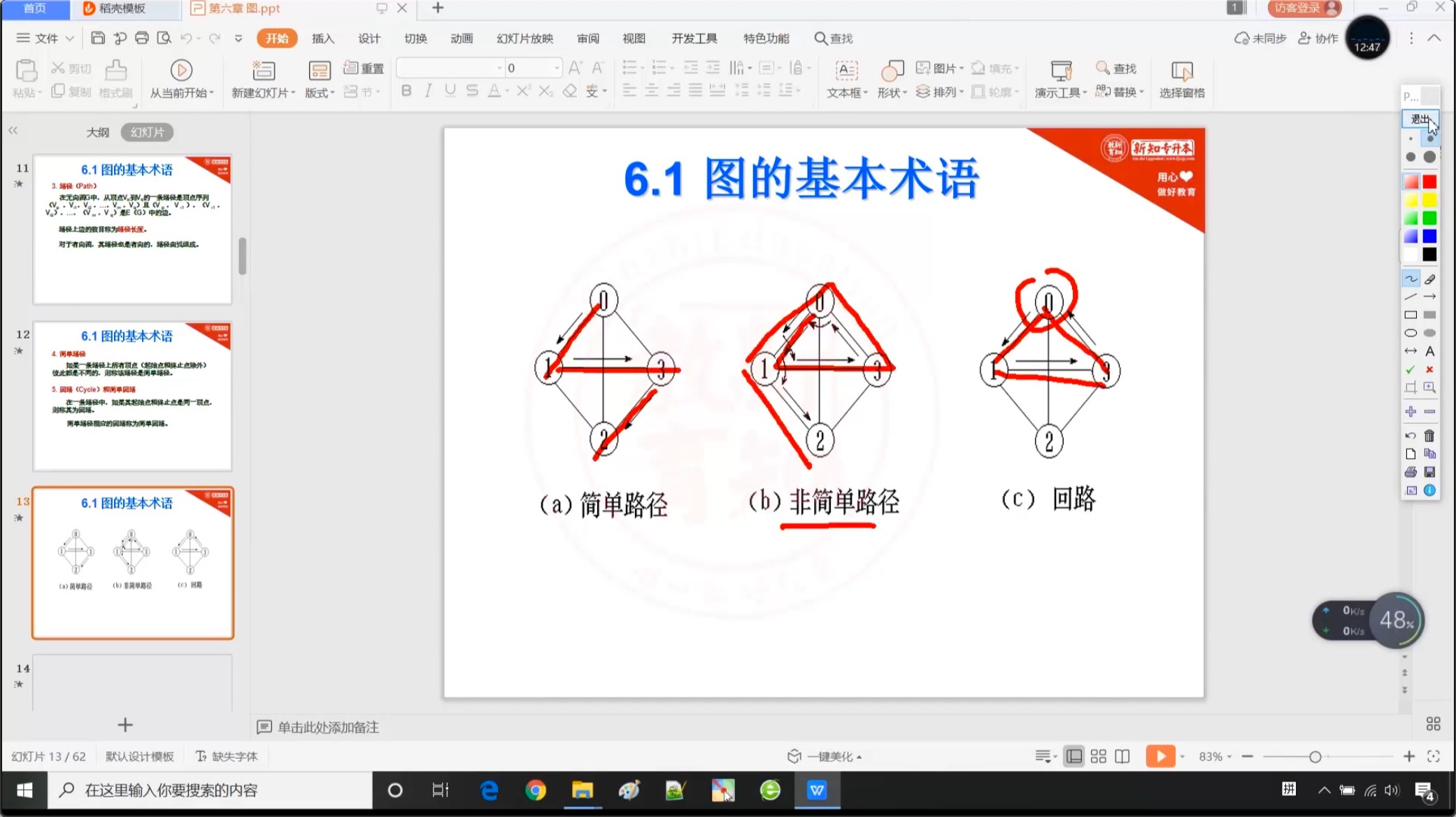
image-20220221133806169

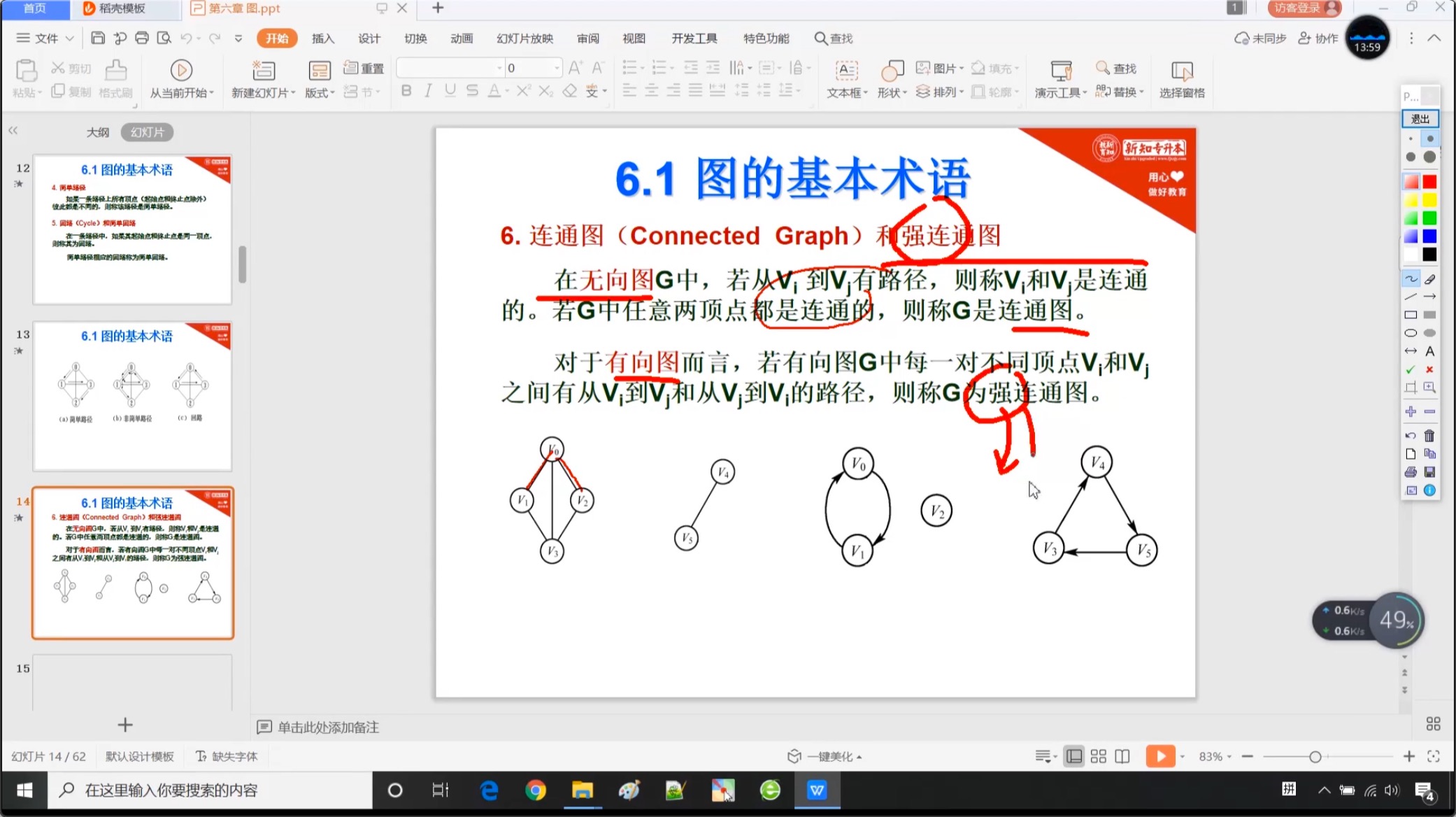
6.1.5 连通图和强连通图

image-20220221133912117

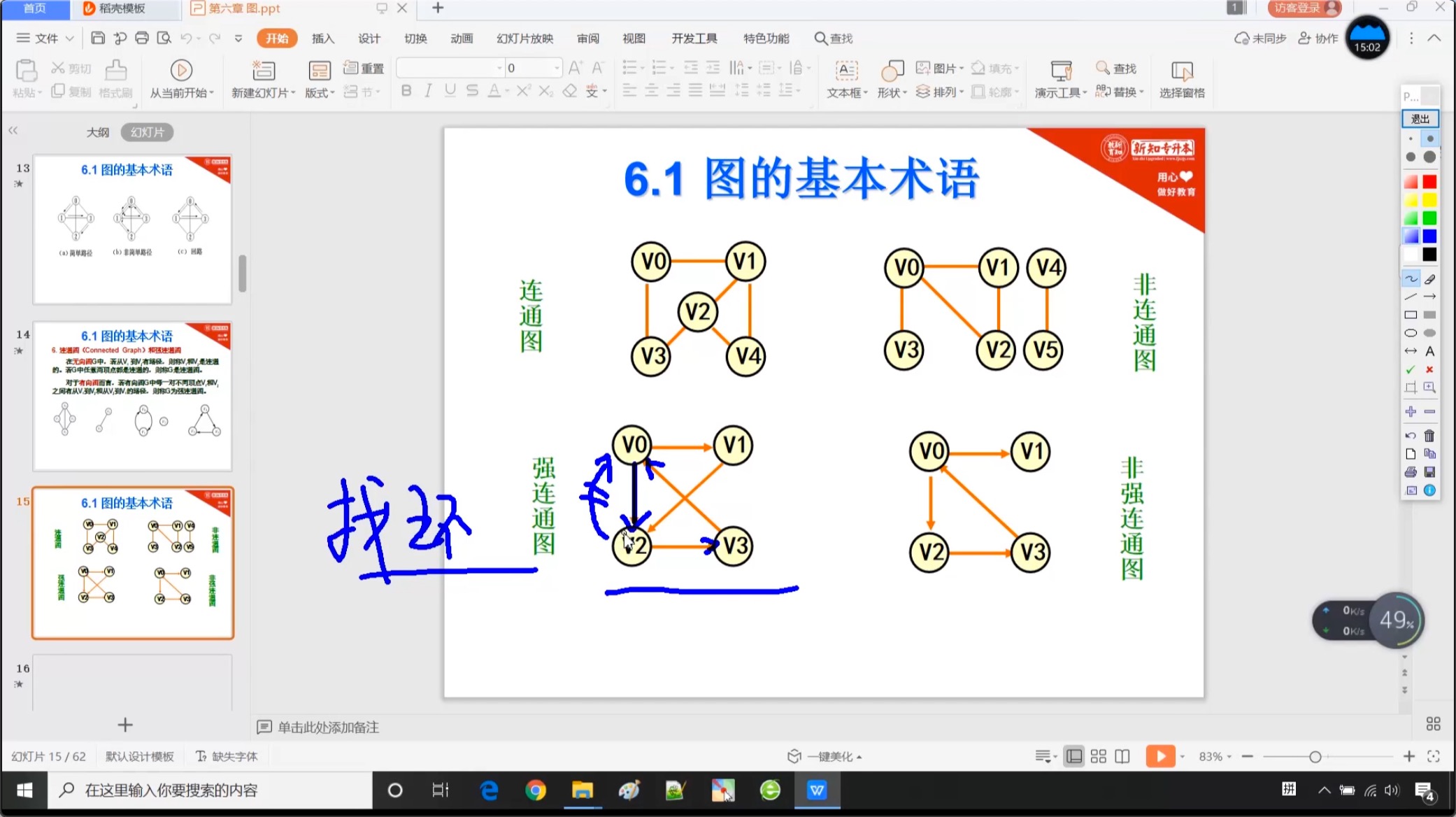
image-20220221134033805

6.1.6 连通分量和强连通分量

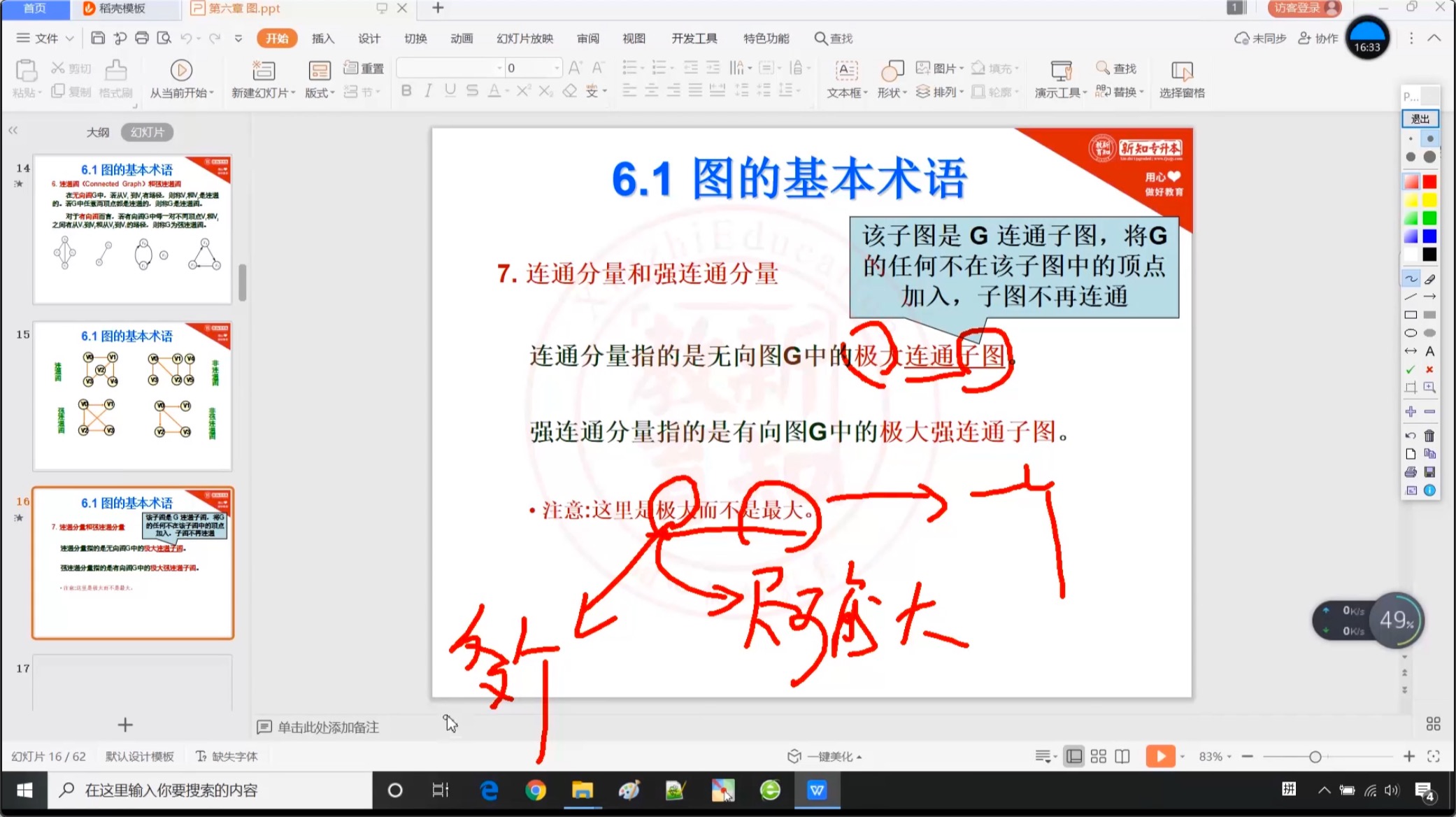
image-20220221134336872

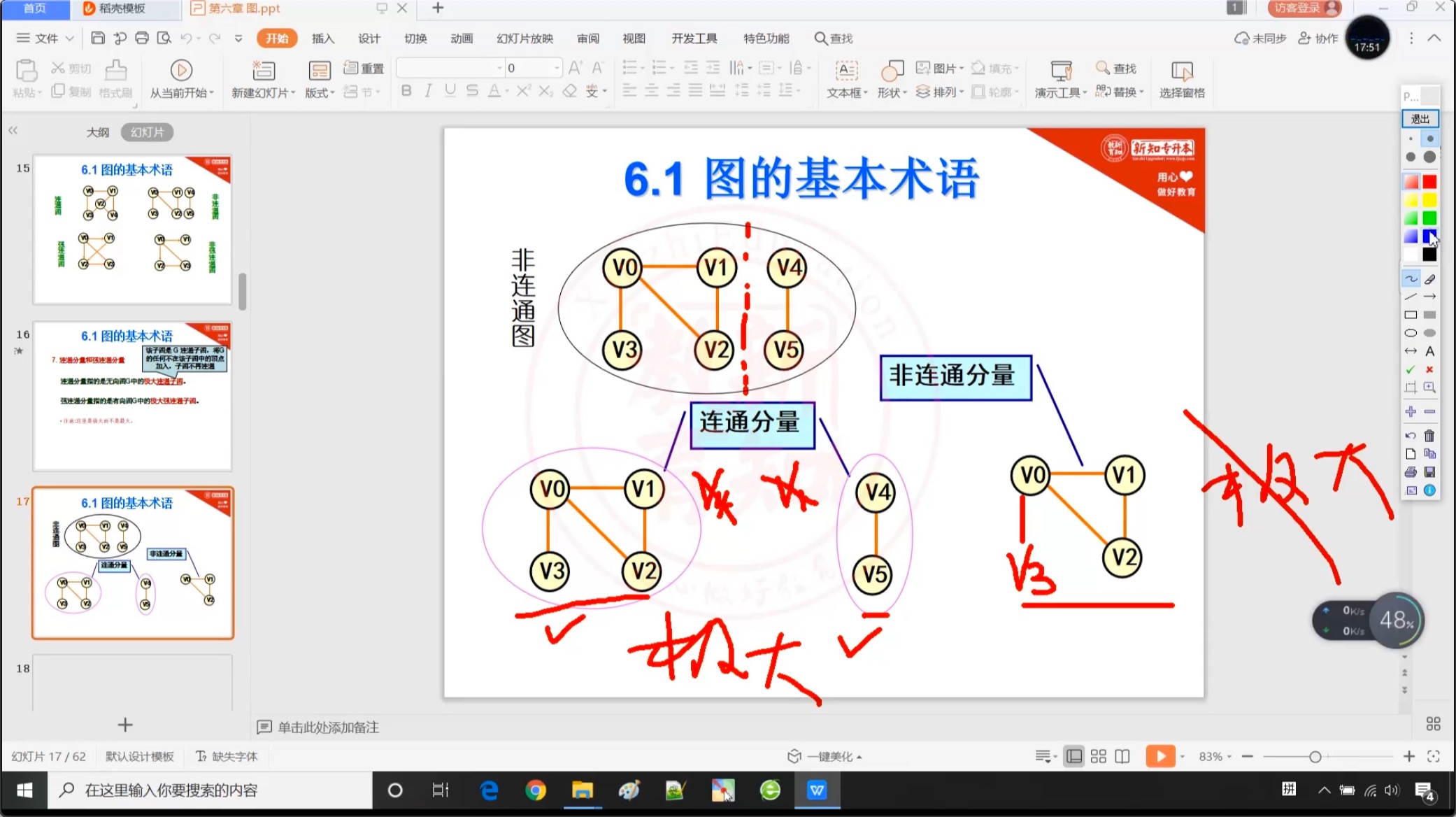
image-20220221134352898

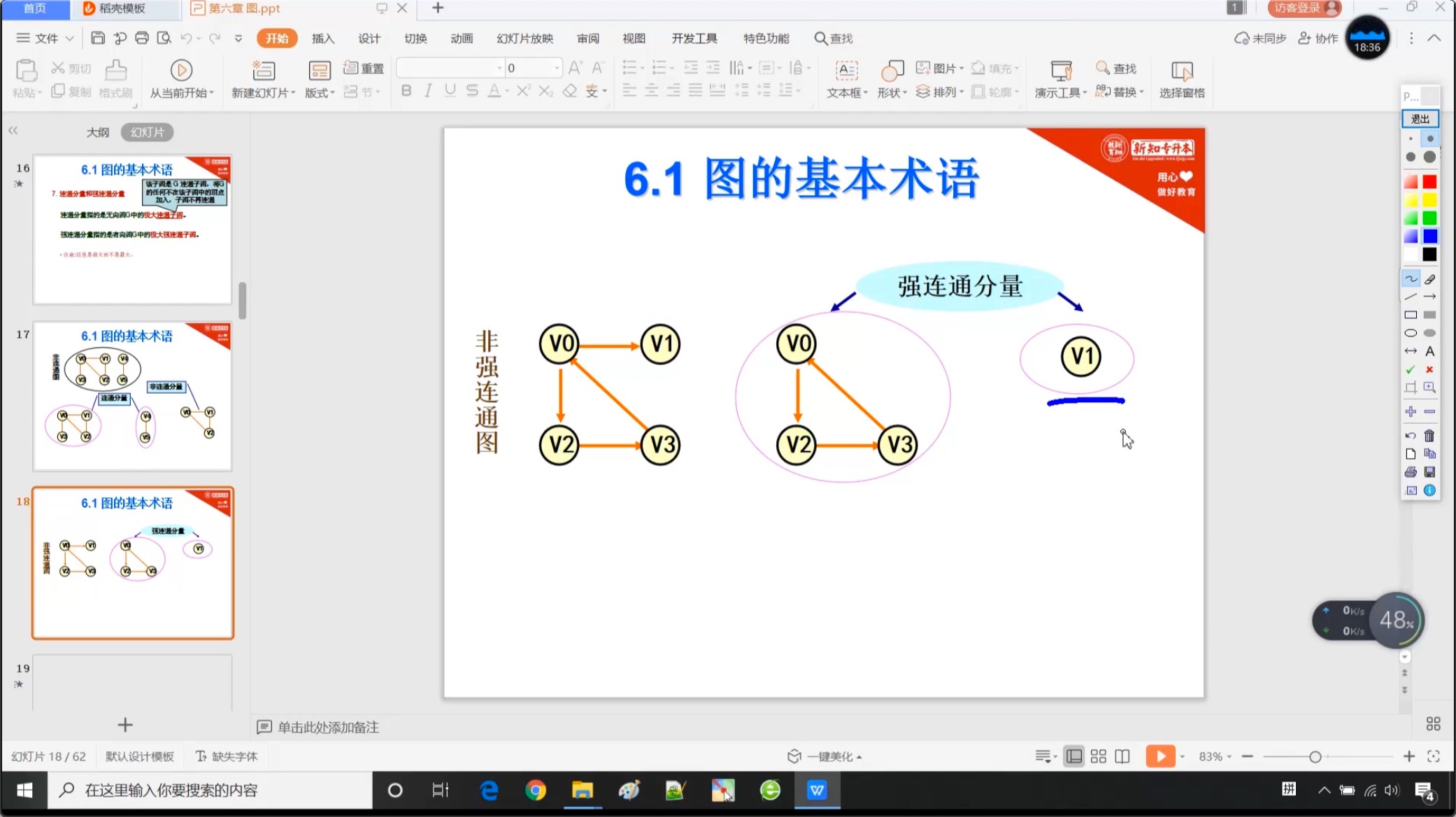
image-20220221134639748

6.1.7 度

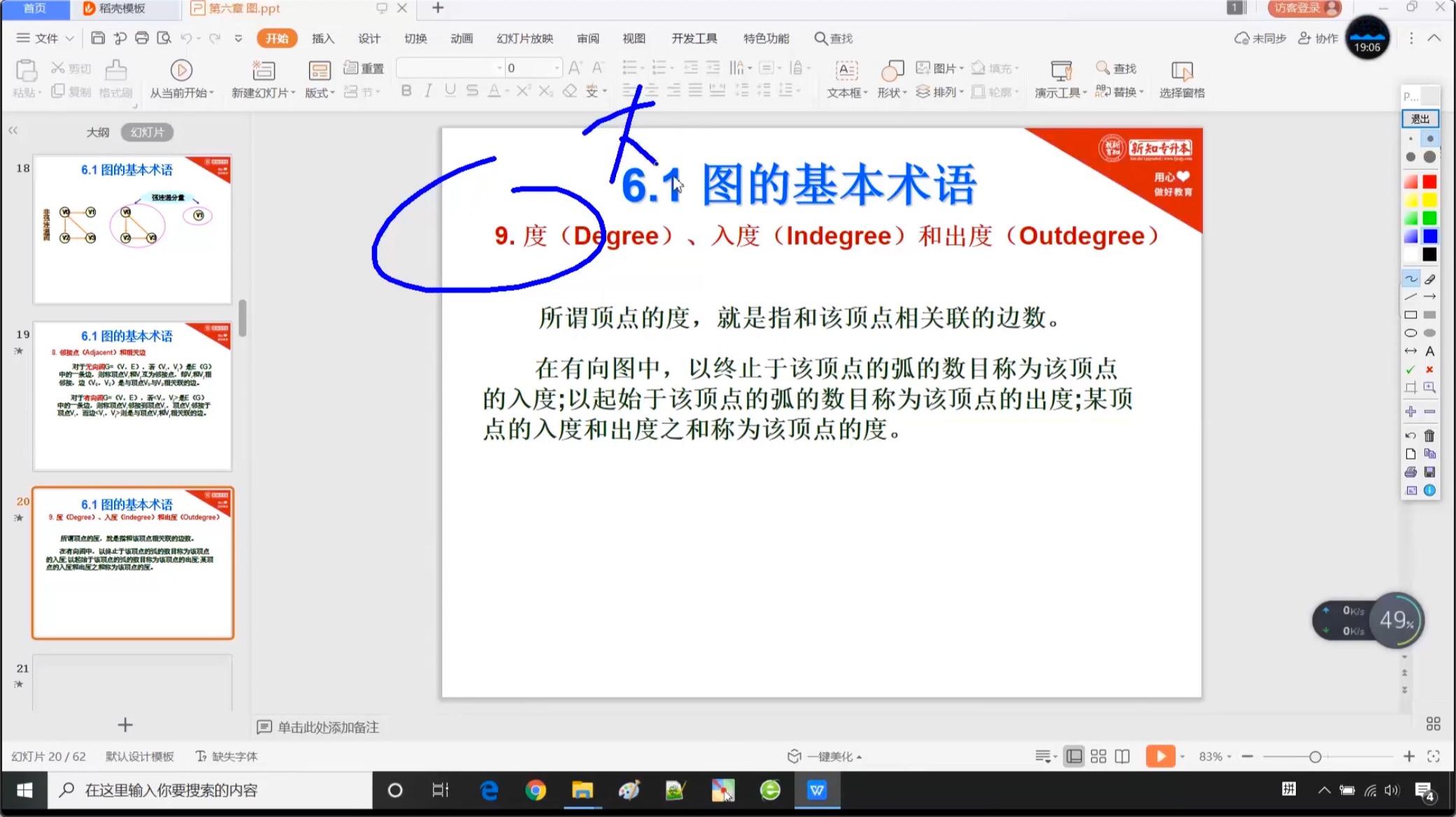
image-20220221134832282

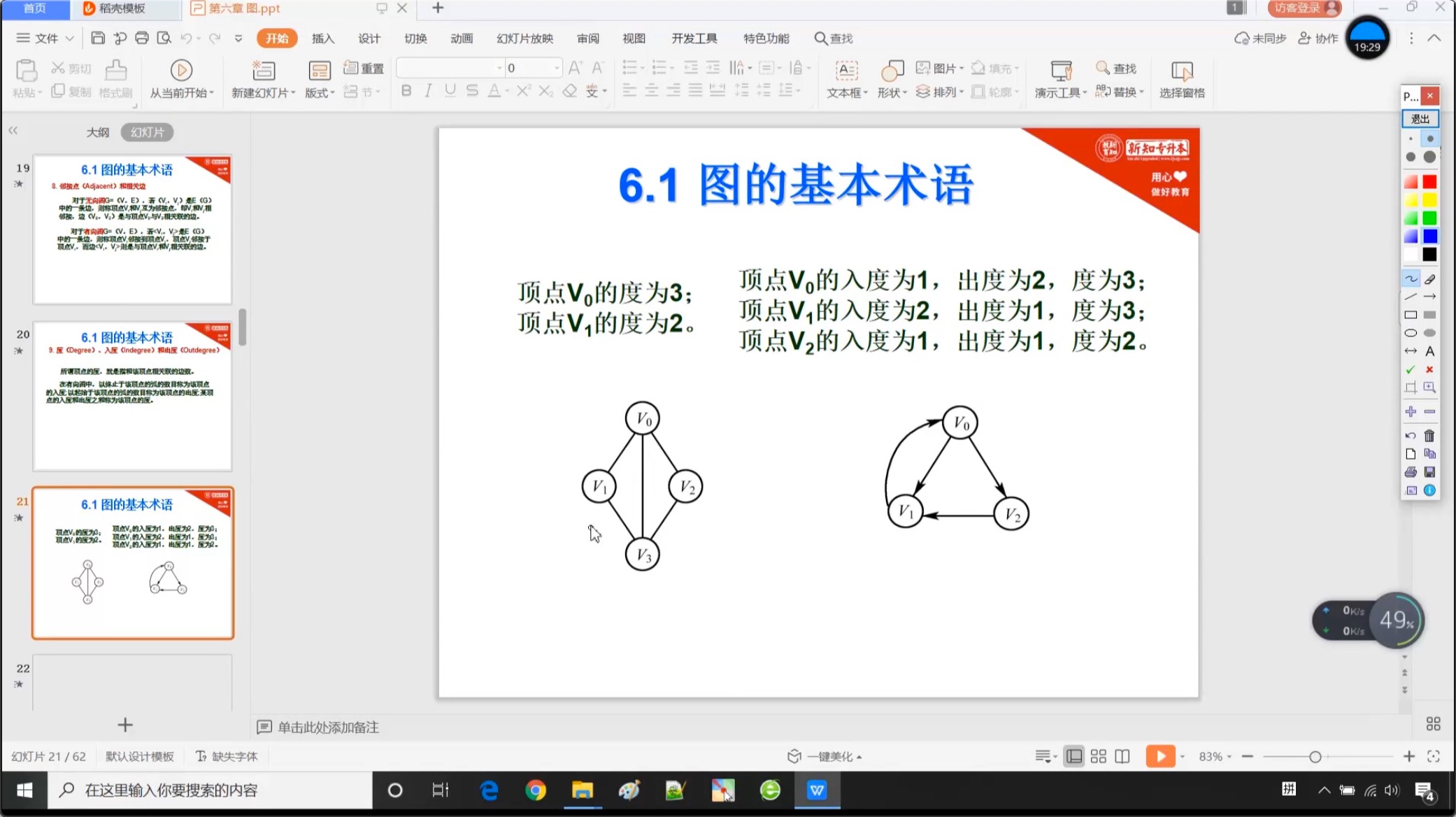
image-20220221134818483

6.1.8 权和网

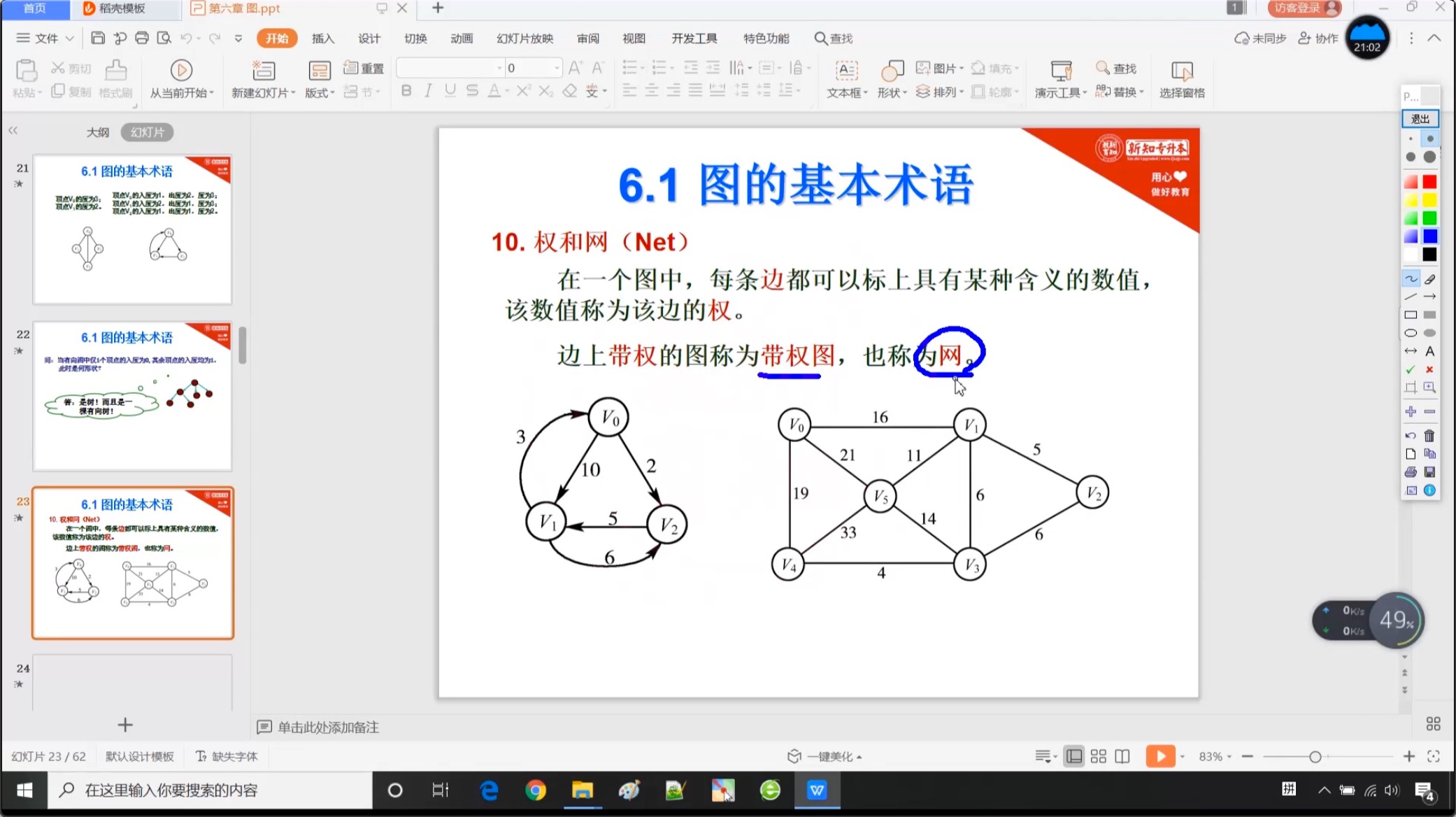
image-20220221135032409

6.2 图的存储结构

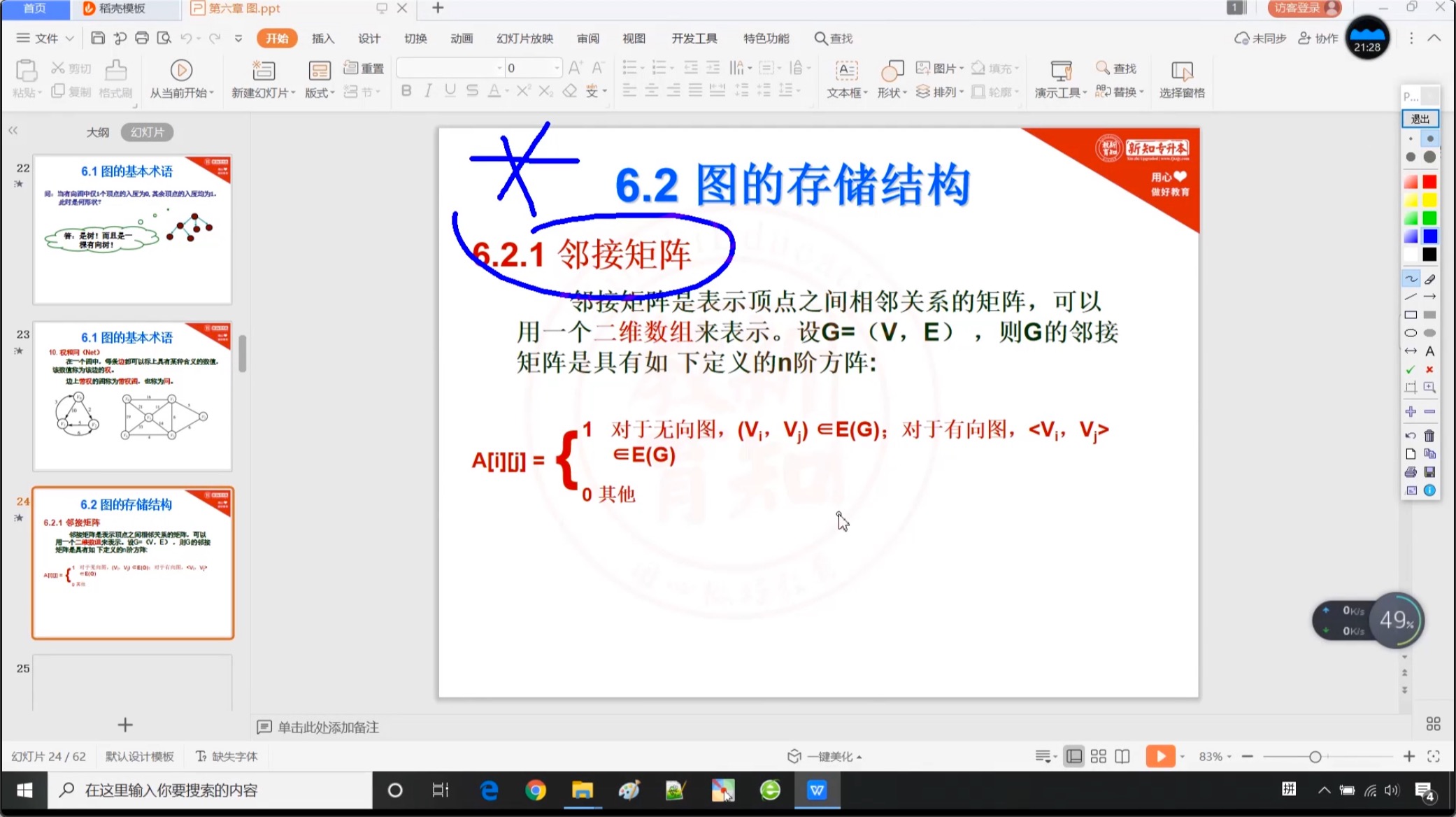
6.2.1 邻接矩阵【重点】

image-20220221135154671

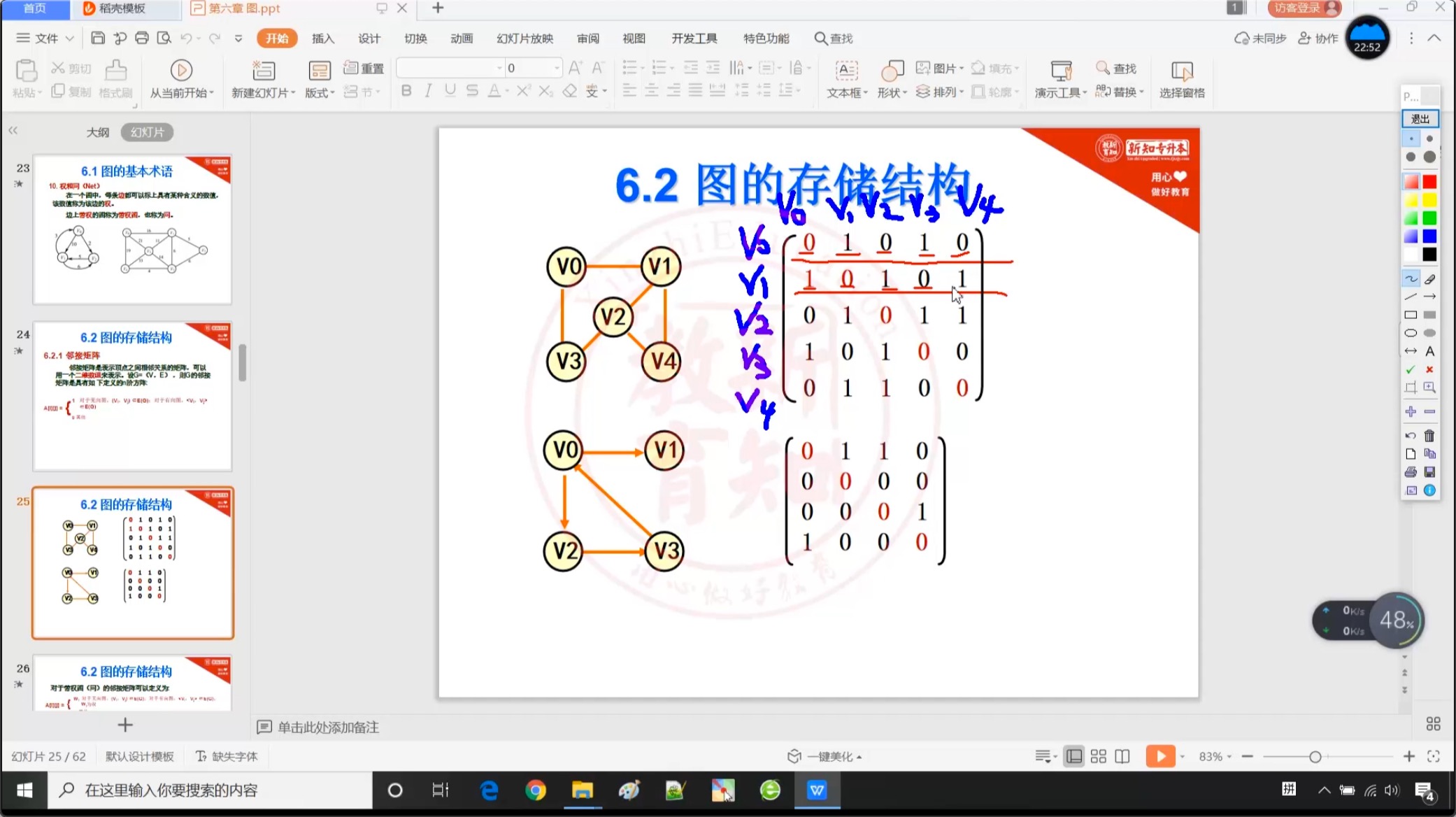
image-20220221135509883

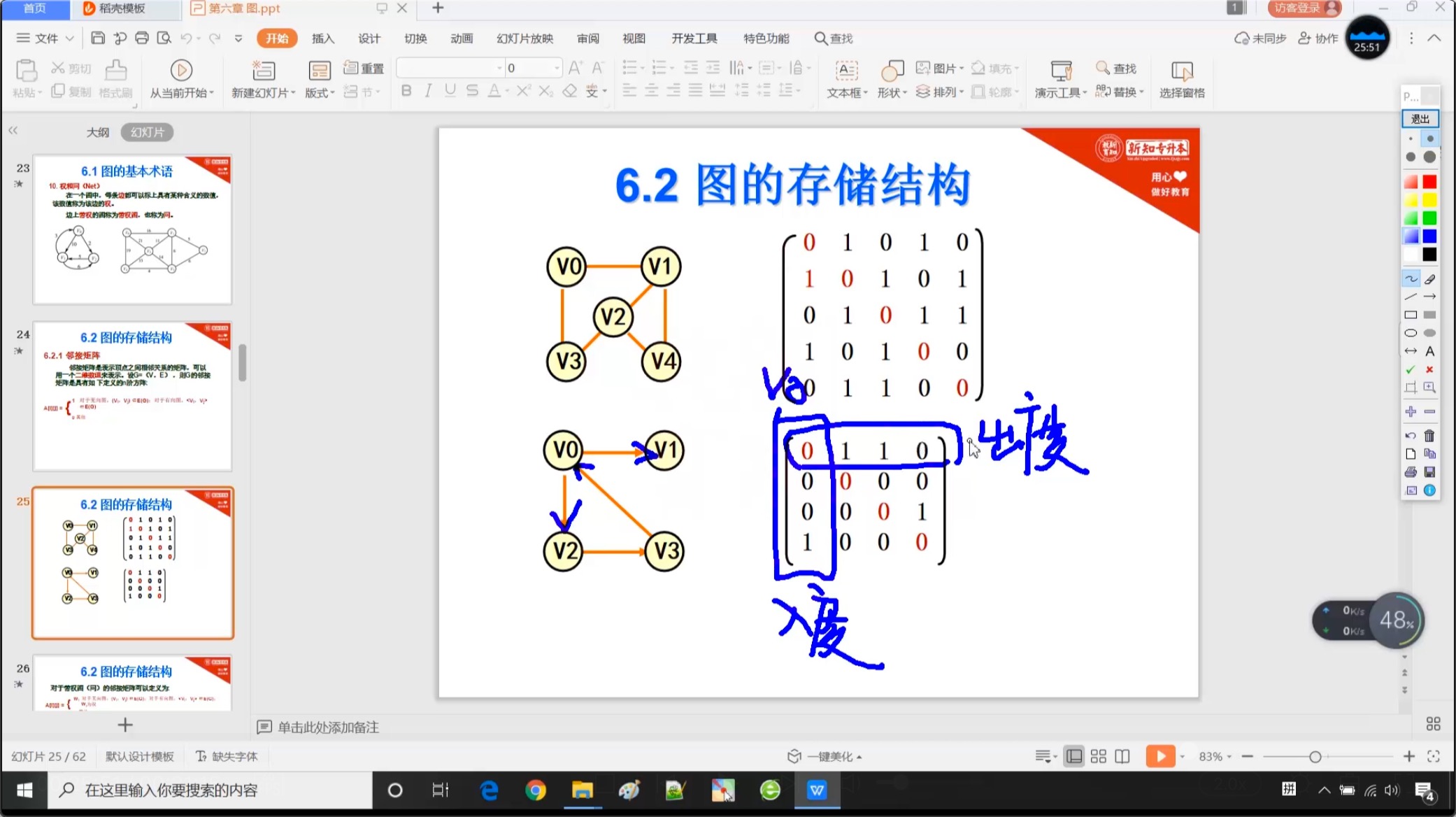
image-20220221135525943

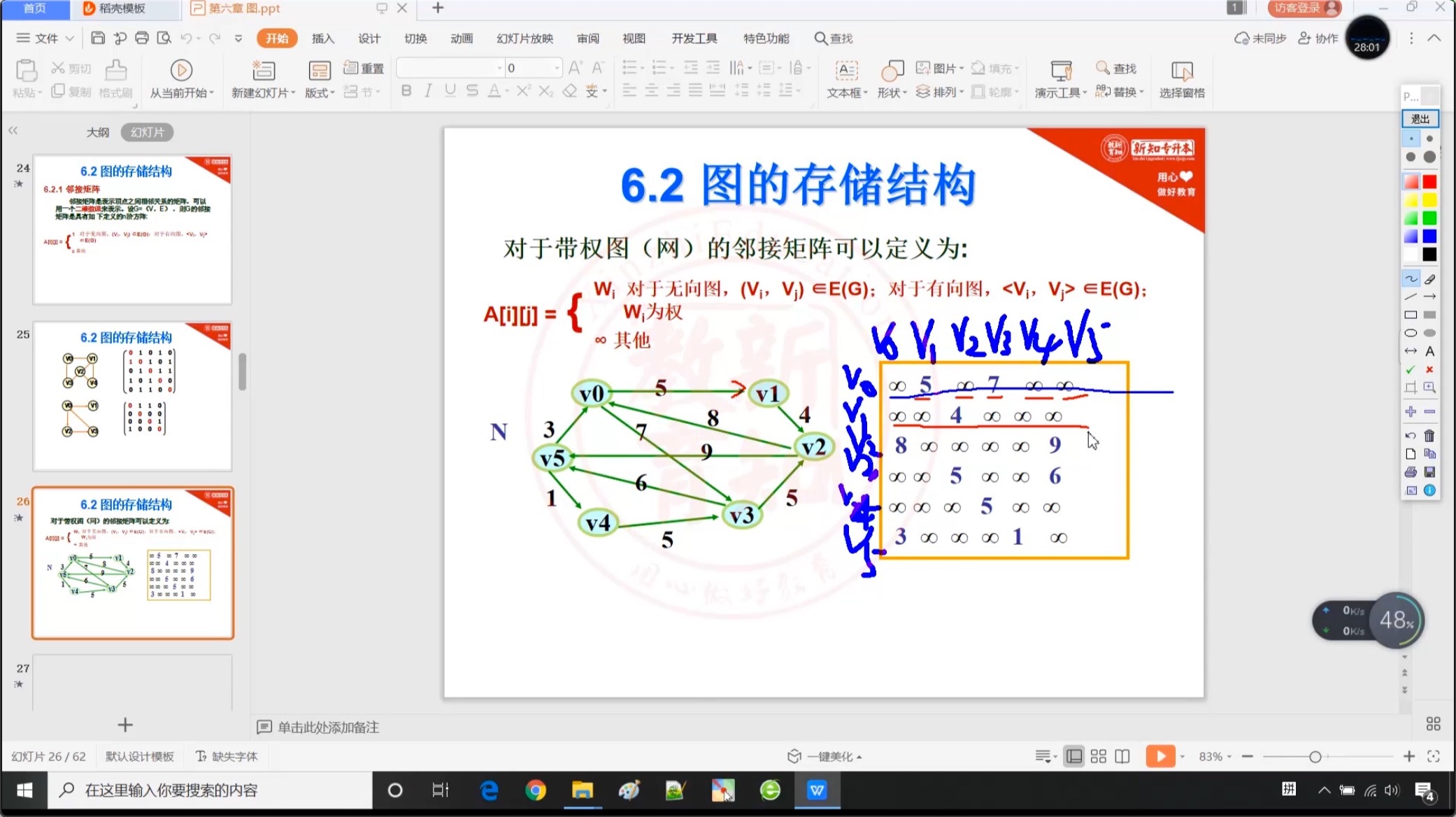
image-20220221135719304

6.2.2 邻接表

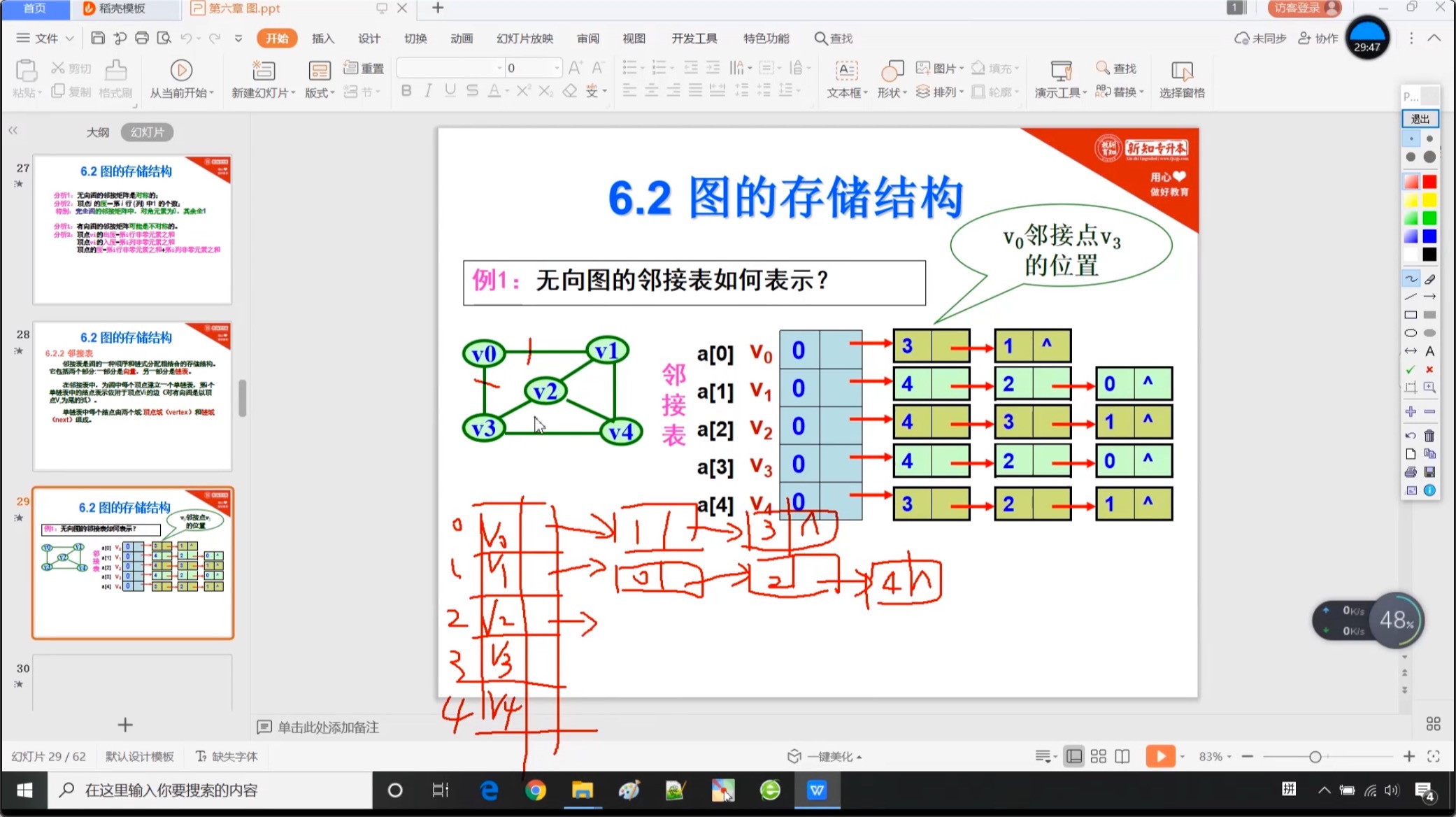
image-20220221140222578

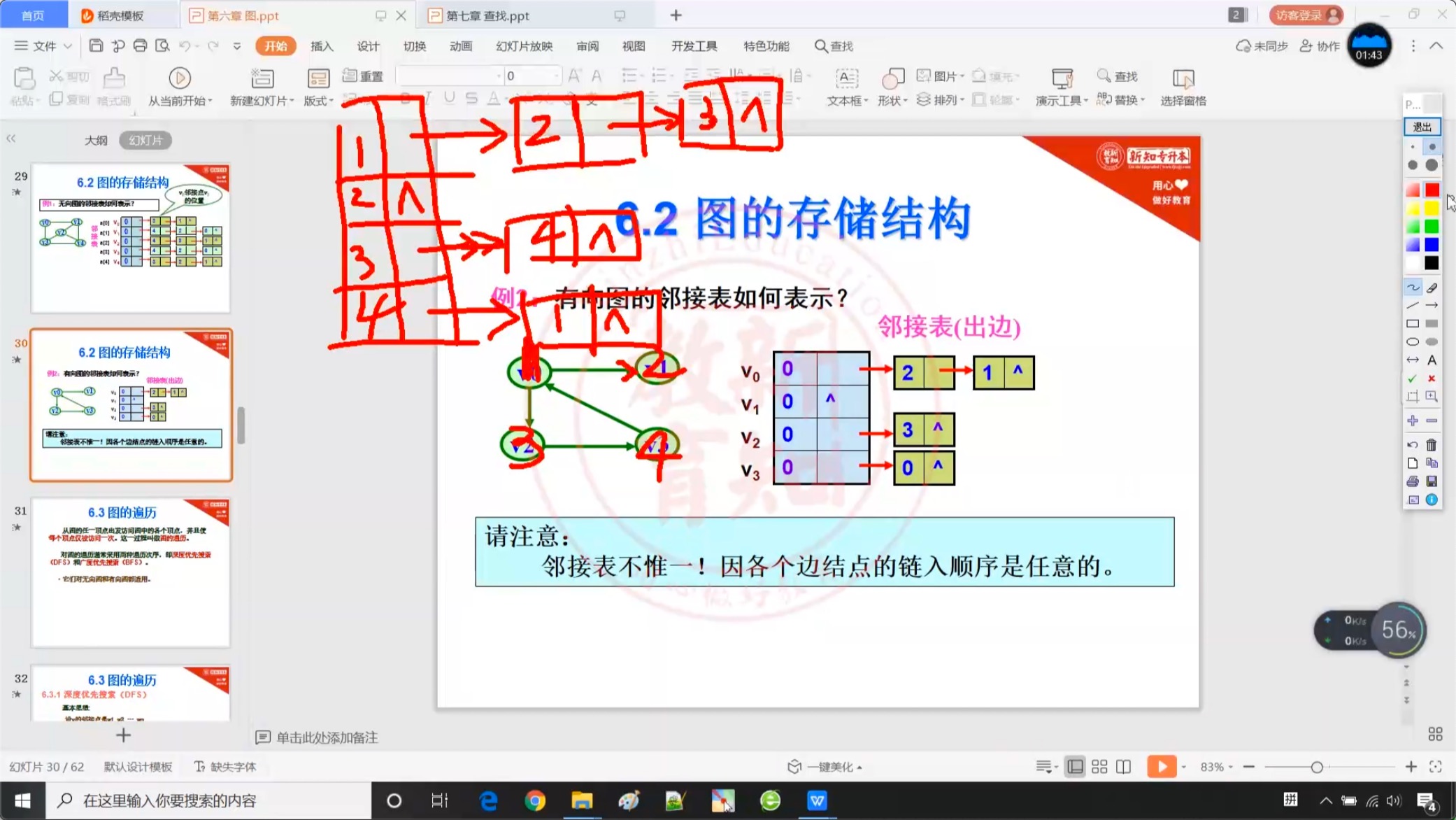
image-20220221140355078

6.3 图的遍历

6.3.1 基本概述

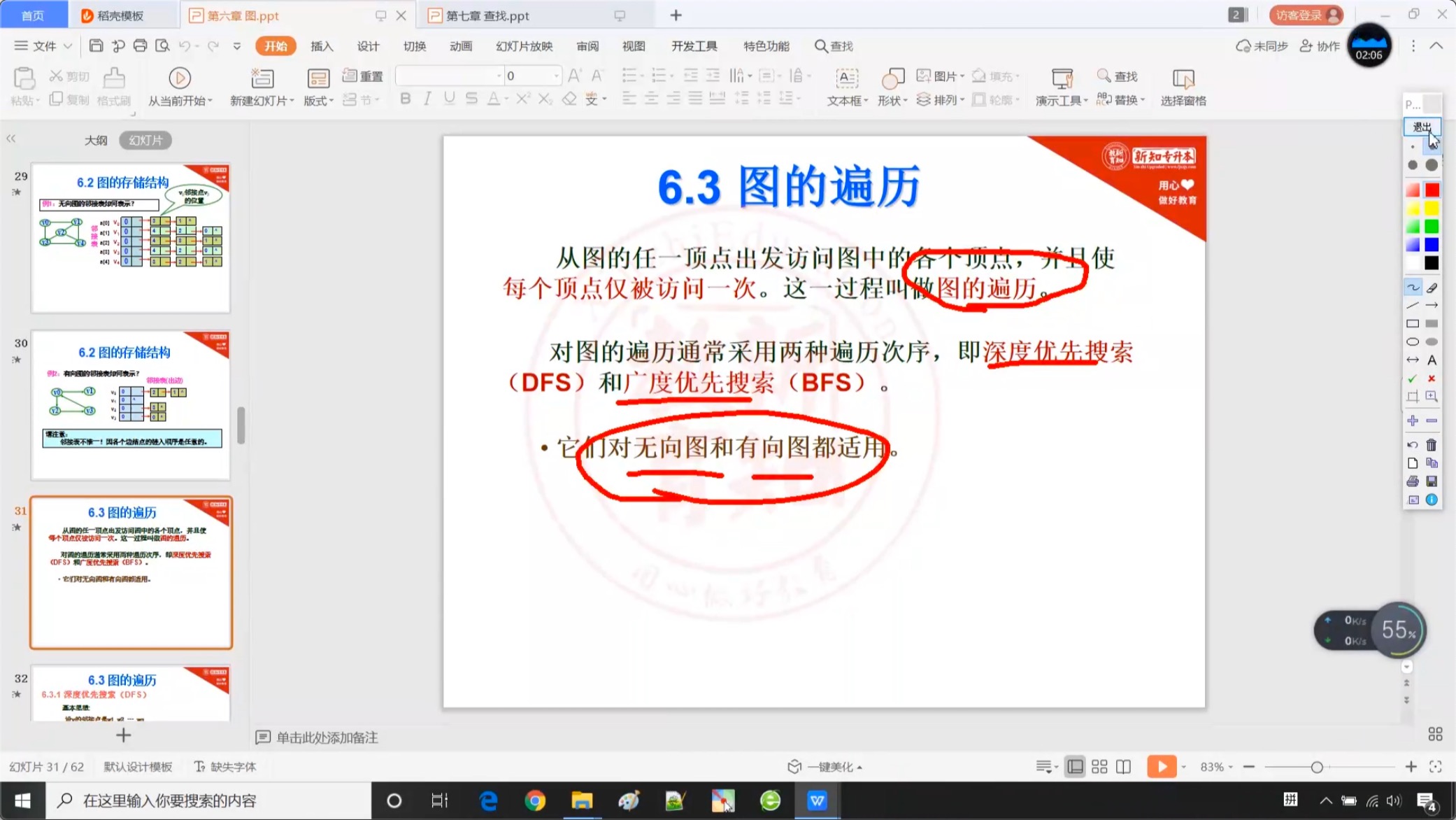
image-20220221140525593

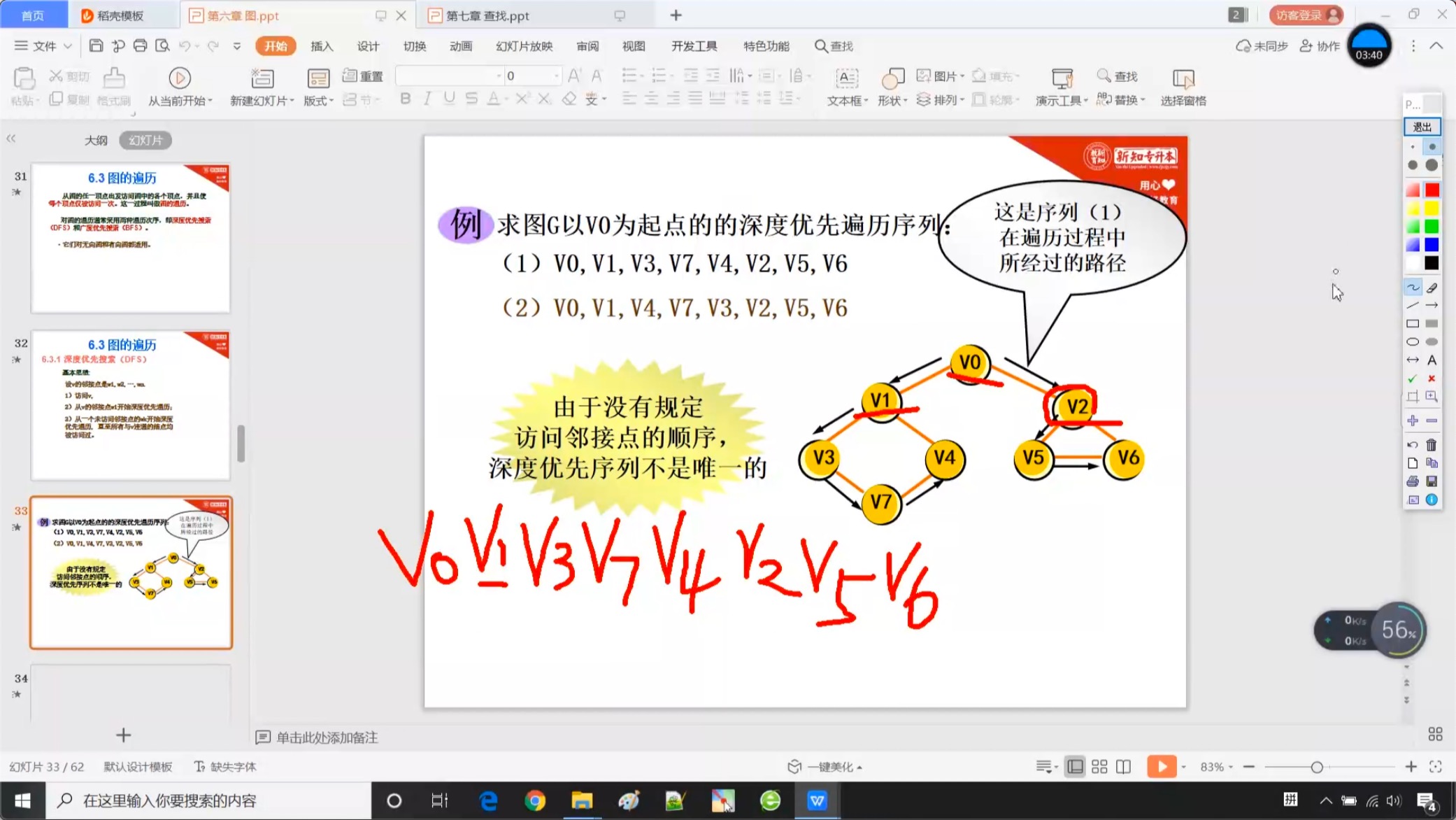
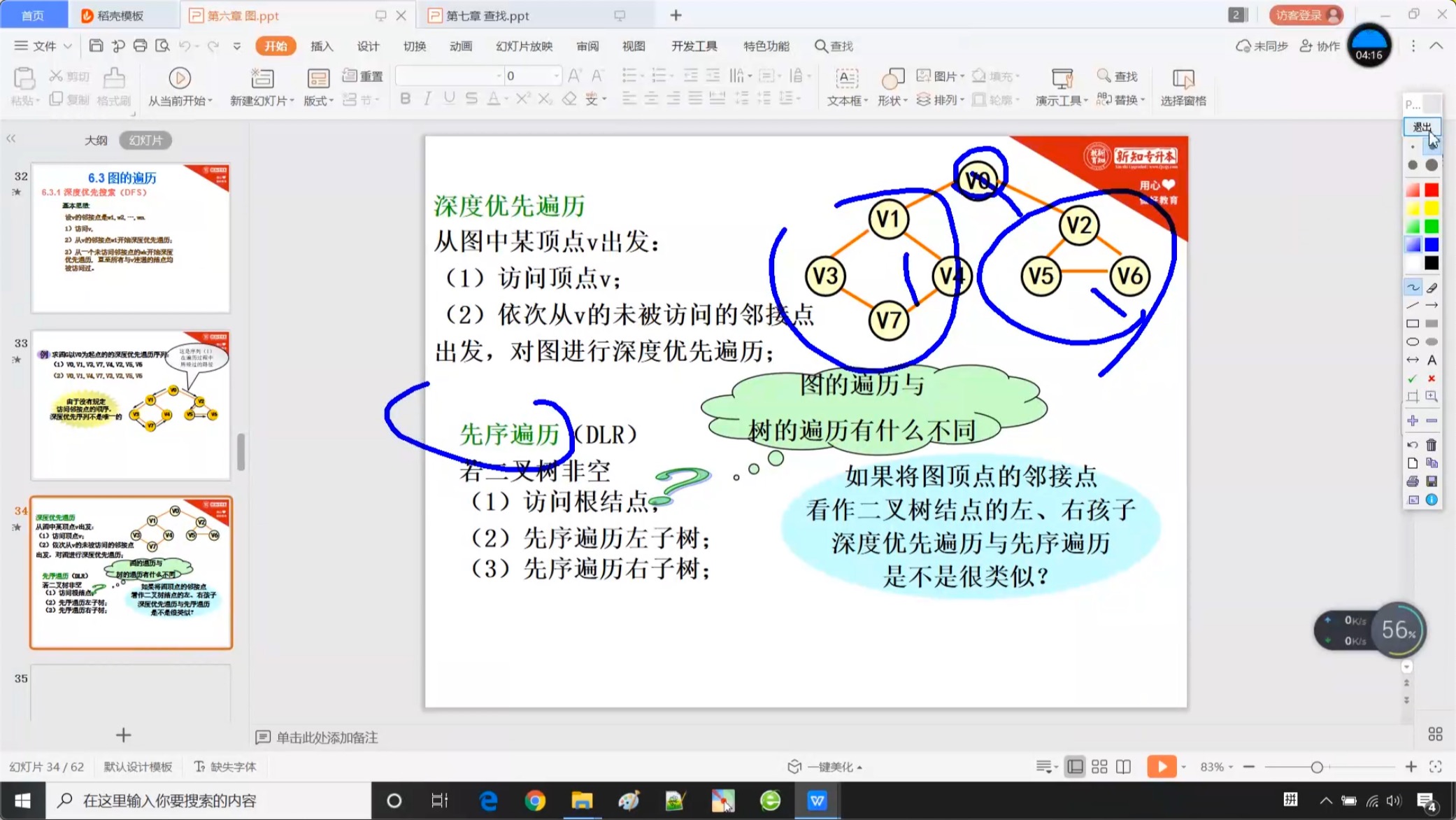
6.3.2 深度优先搜索

image-20220221140715509

image-20220221140802708

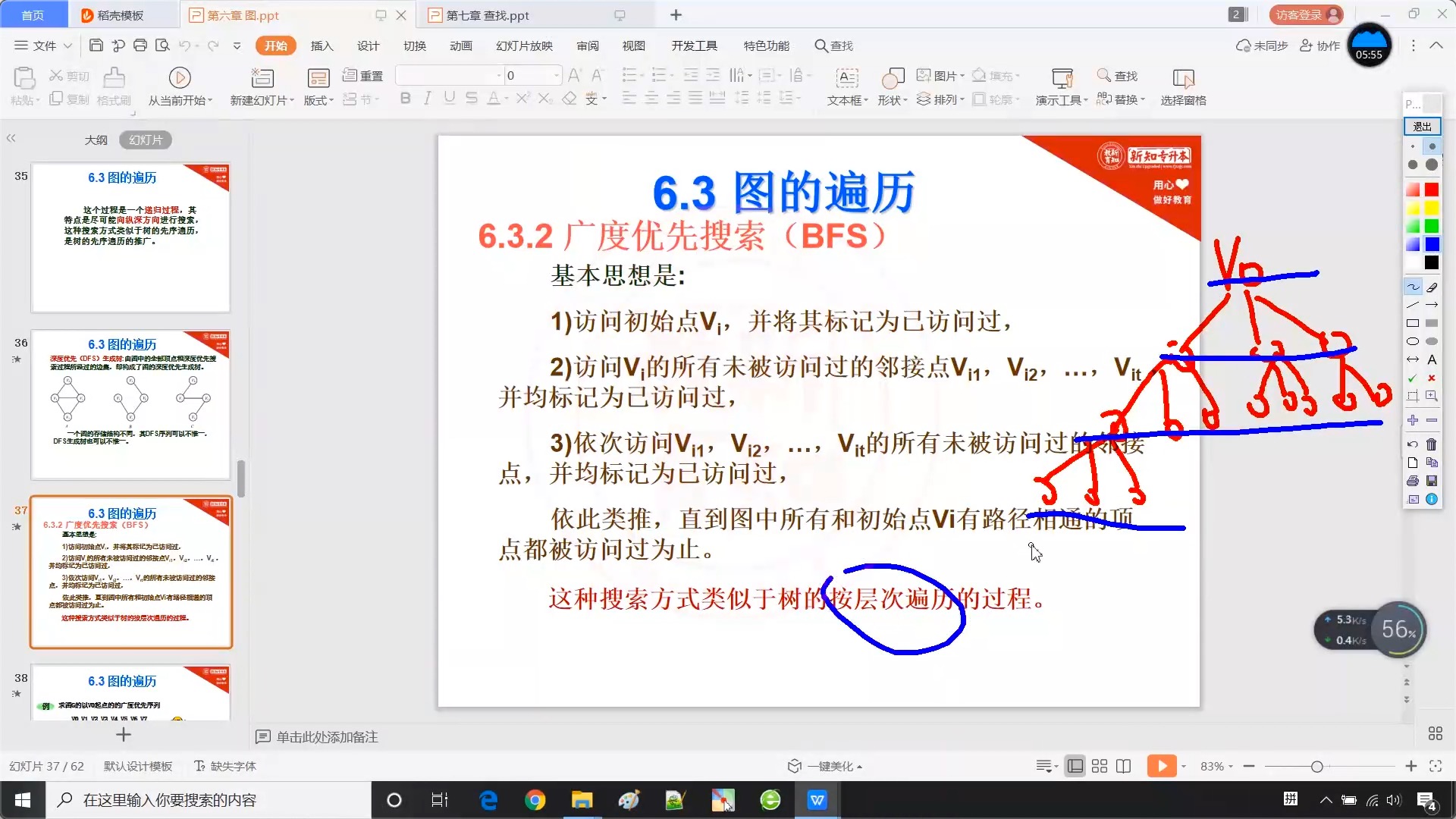
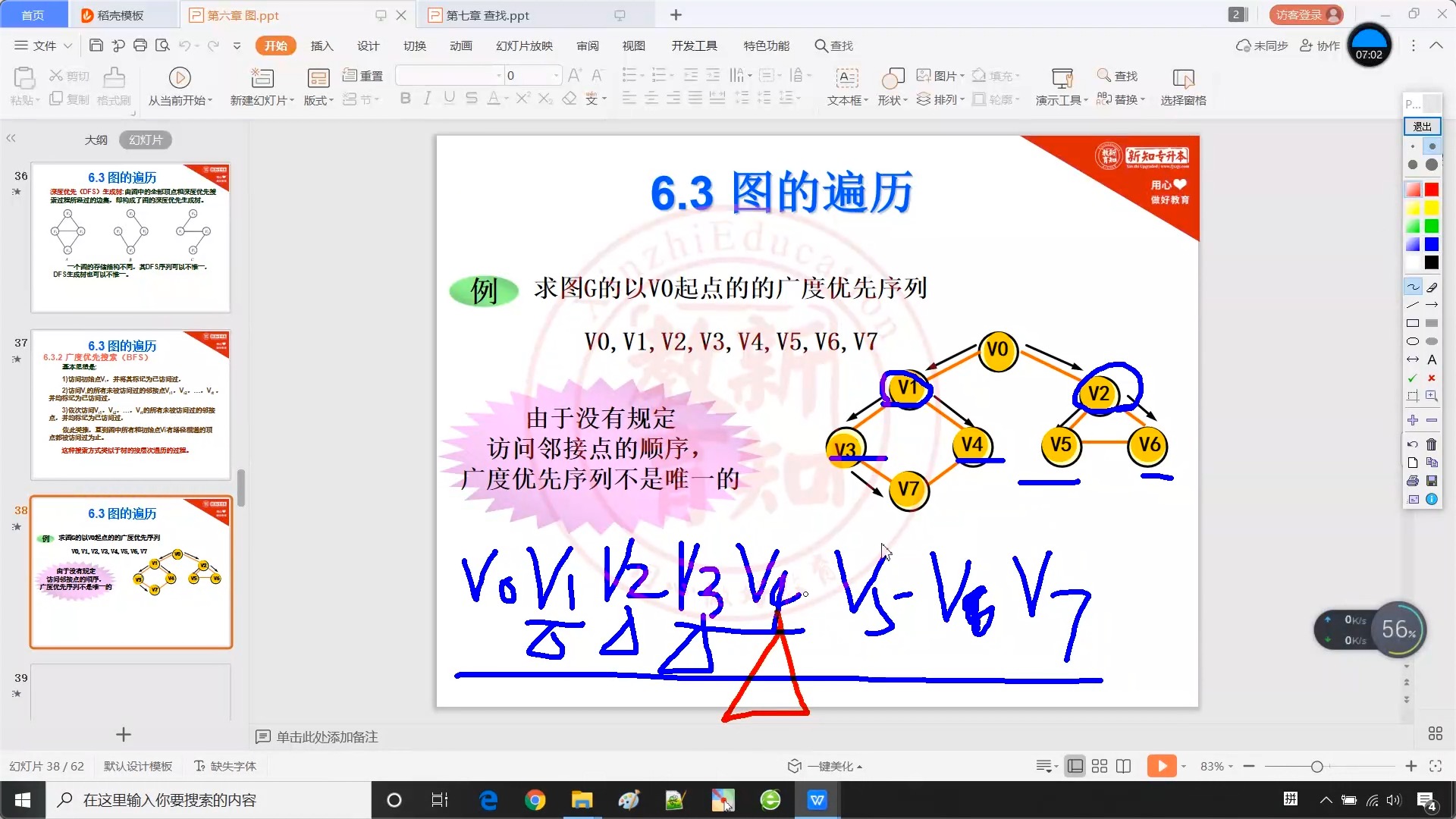
6.3.3 广度优先搜索

image-20220221155051886

image-20220221155110614

image-20220221155133709

6.4 最小生成树

6.4.1 基本概述

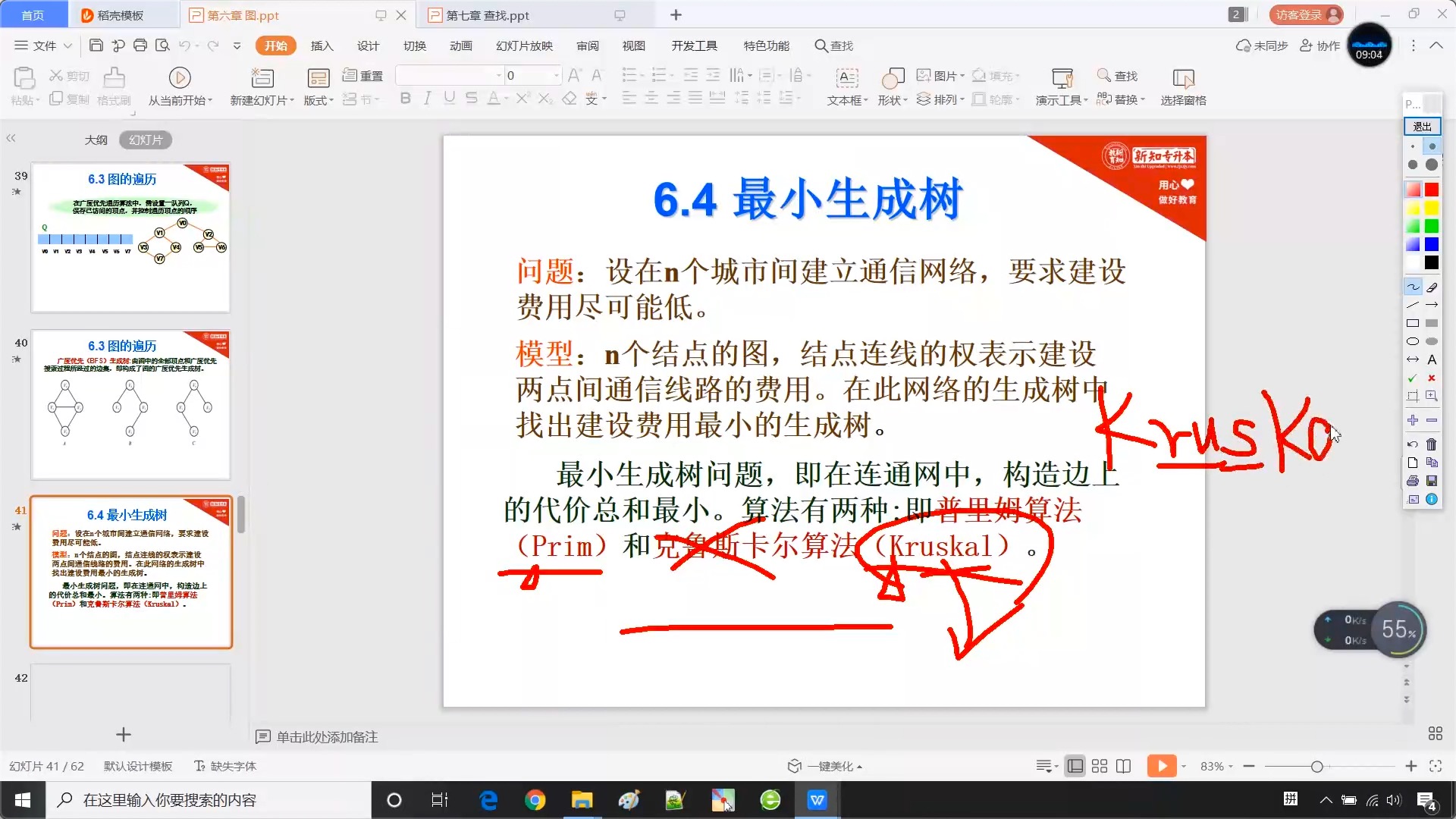
image-20220221155214273

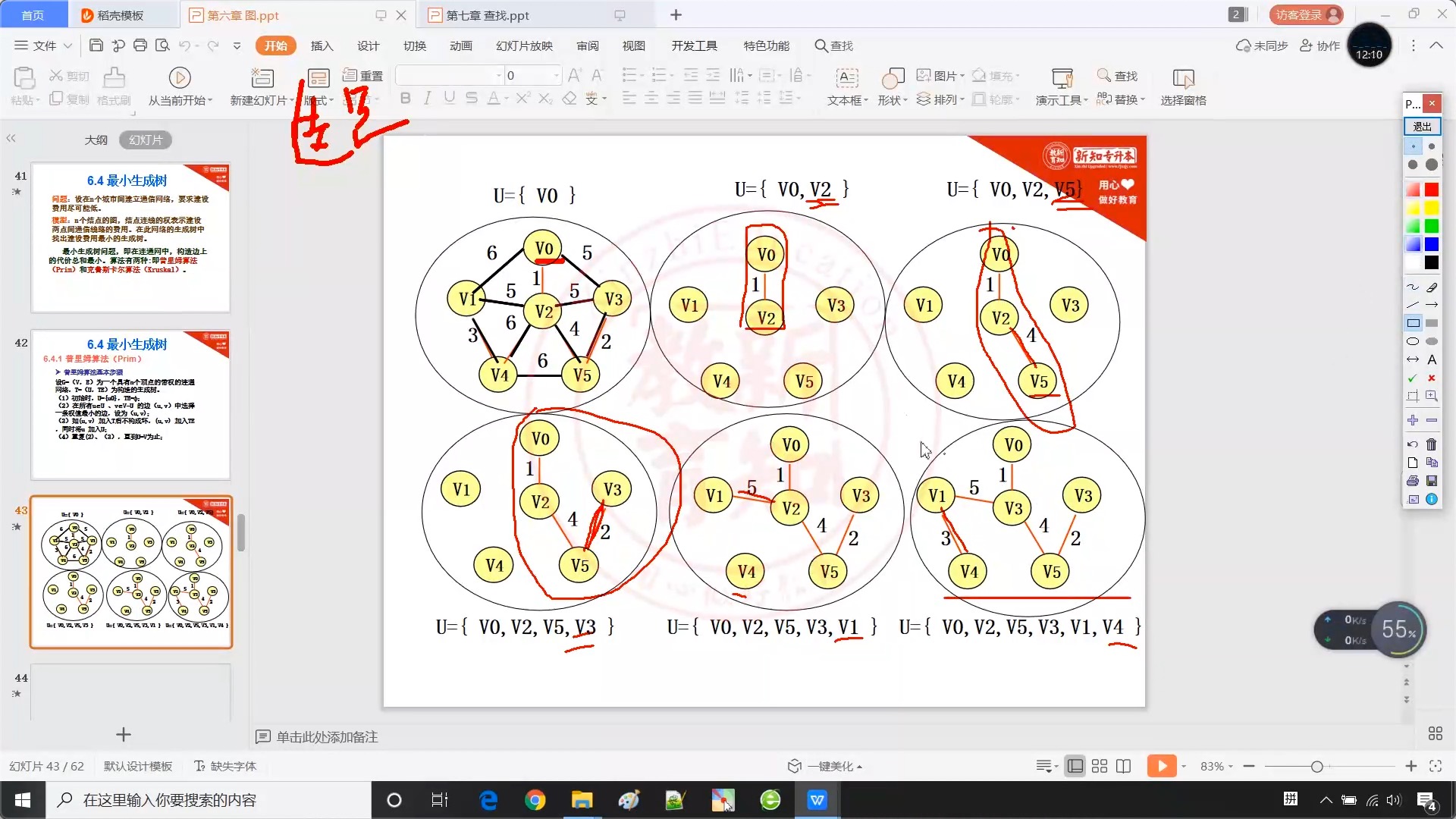
6.4.2 普里姆算法(Prim)

image-20220221155541691

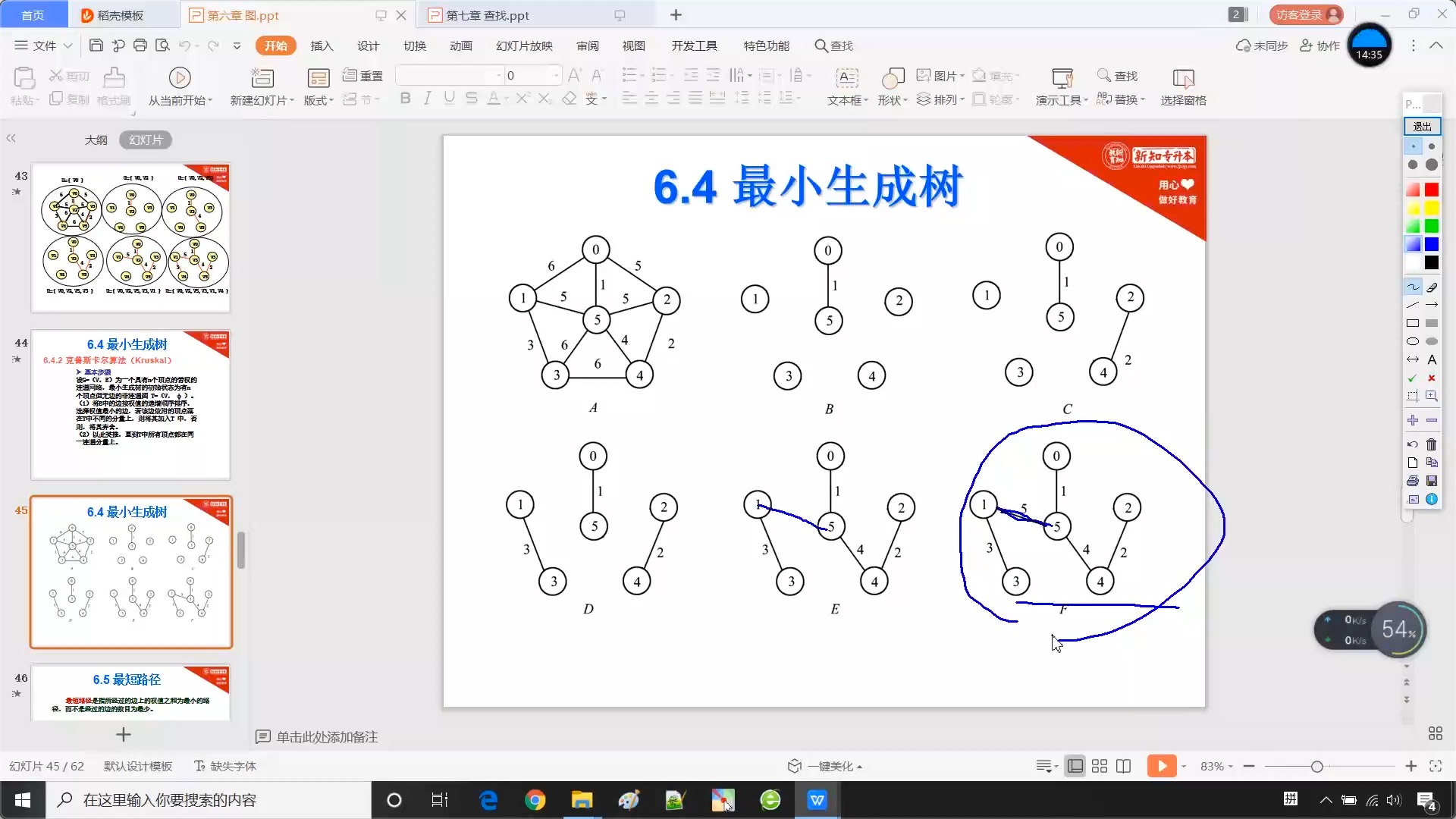
6.4.3 克鲁斯卡尔算法(kruskal)

image-20220221155721279

6.5 最短路径

6.5.1 基本概述

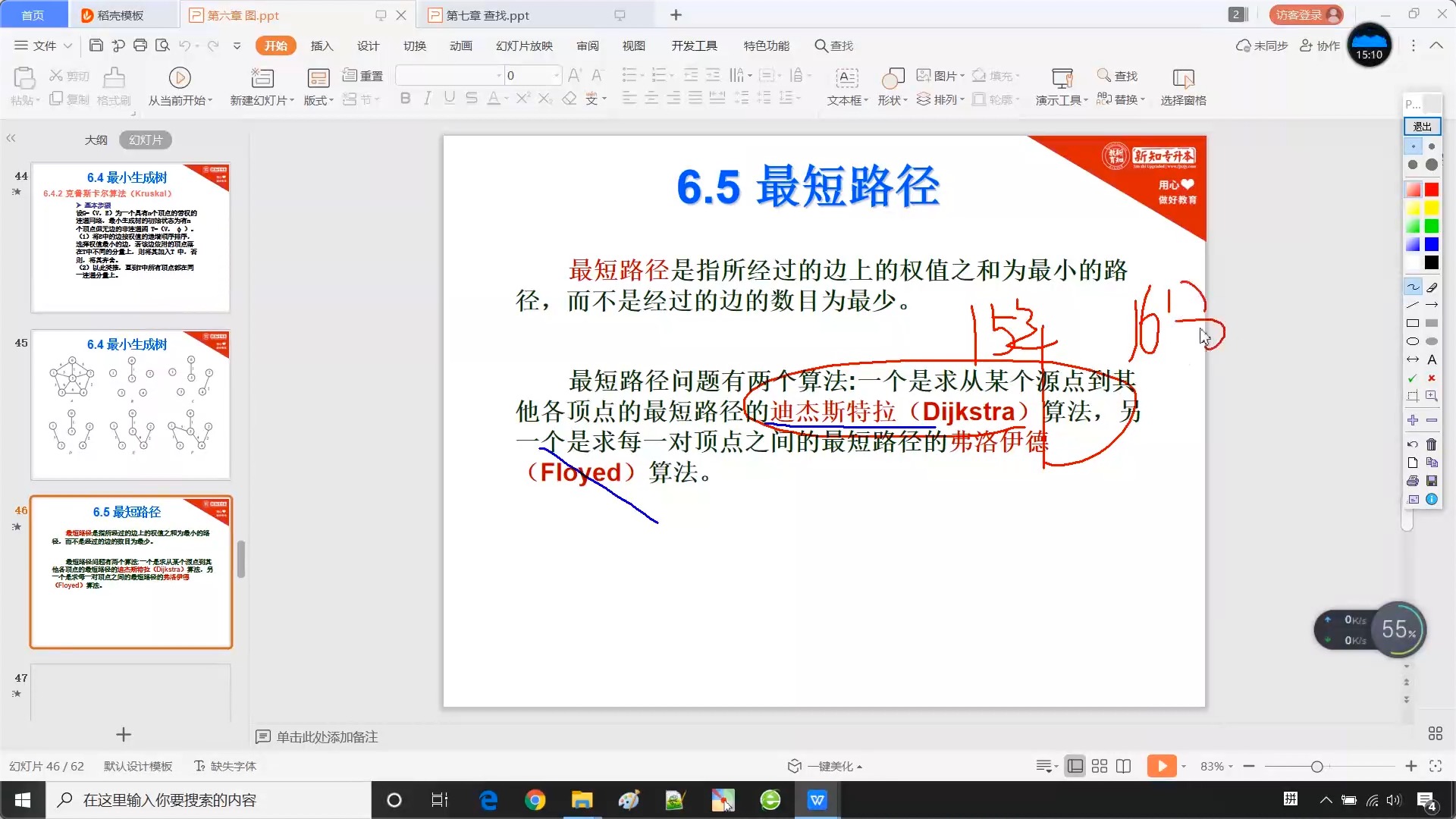
image-20220221155808633

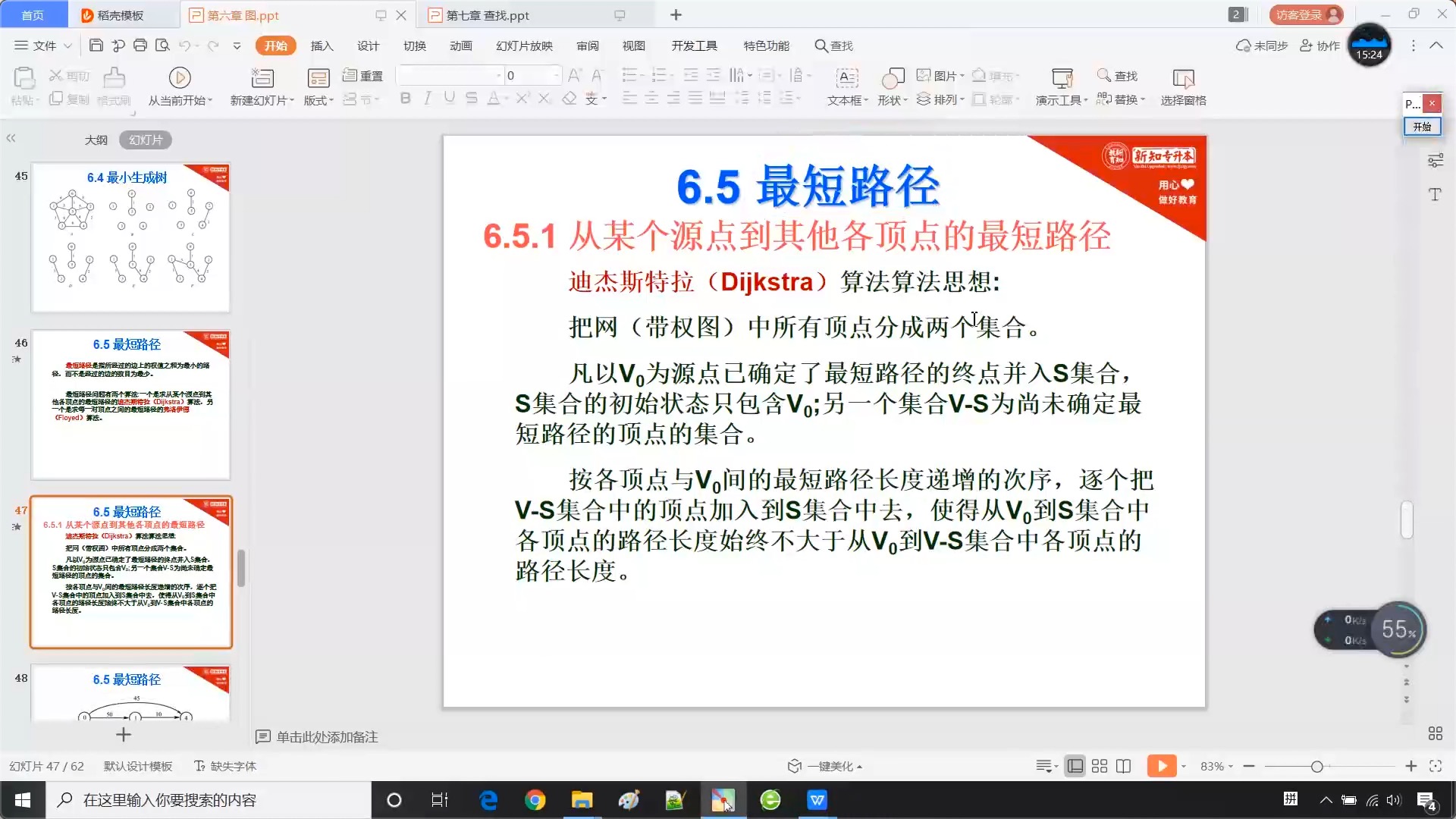
image-20220221155836555

?

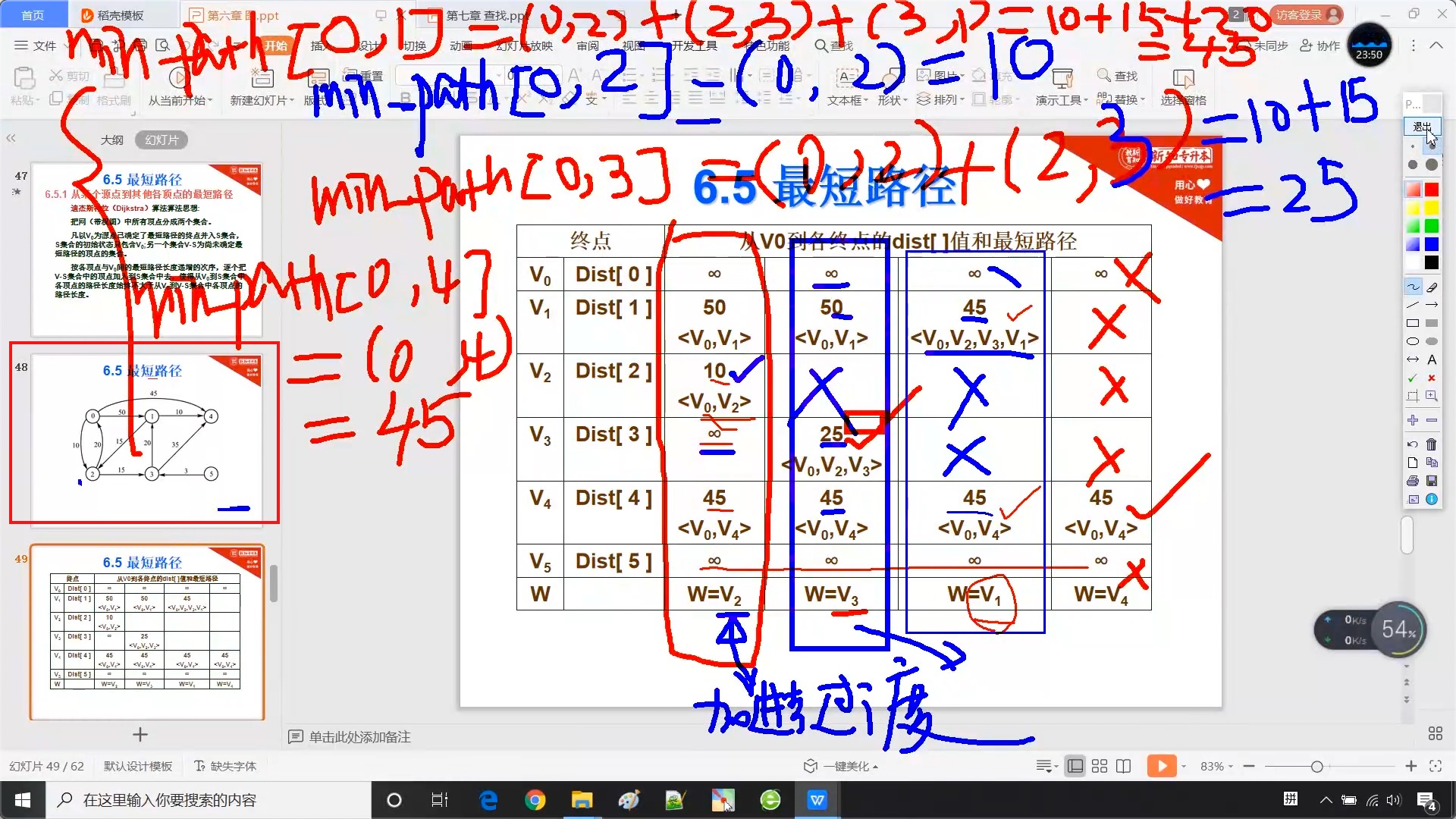
6.5.2 求最短路径

  • 单源最短路径的时间复杂度为O(n2)
  • 多源最短路径的时间复杂度为O(n3)

image-20220221160521049

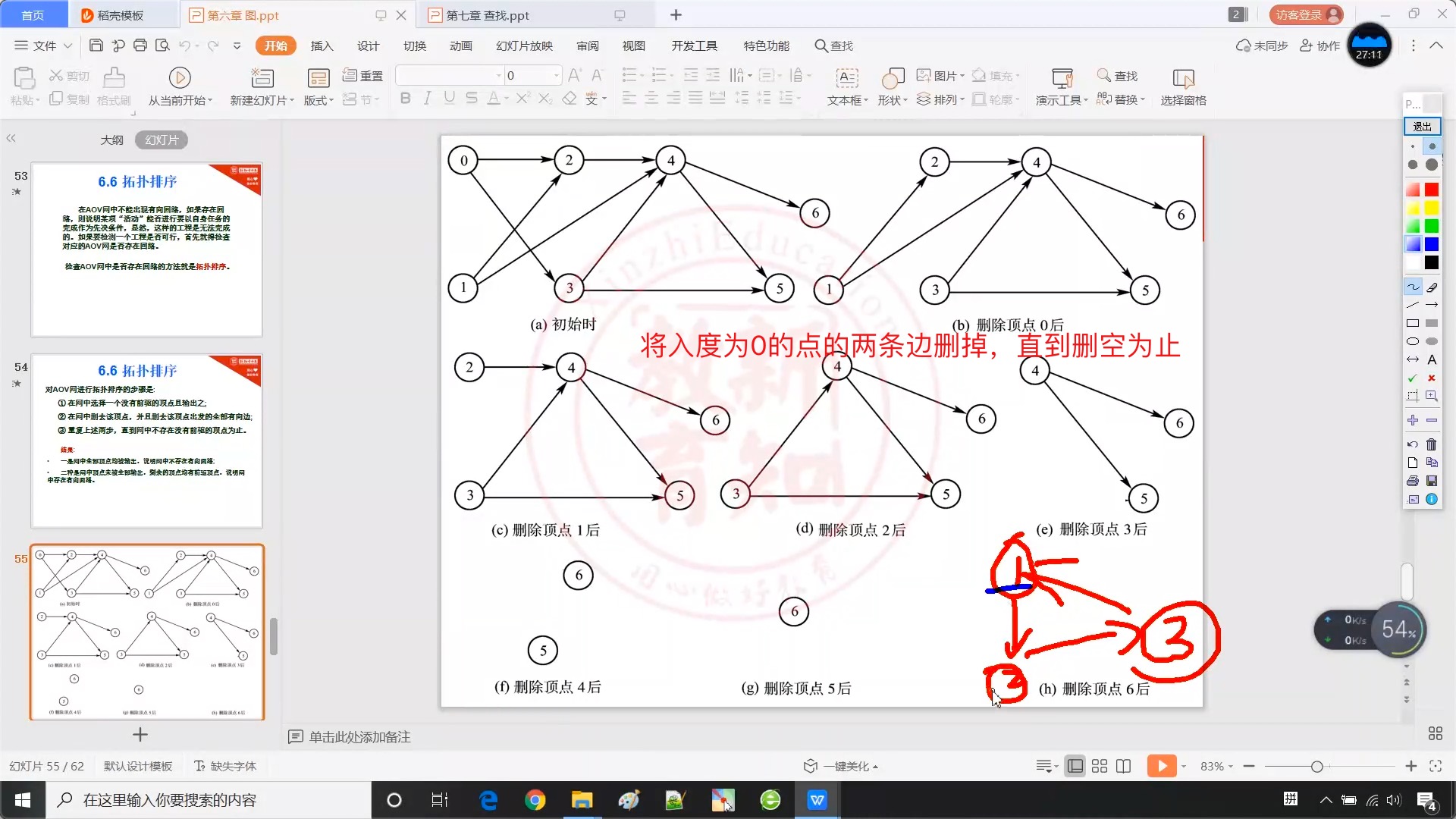
6.6 拓扑排序（了解）

image-20220221160923614

image-20220221161042118

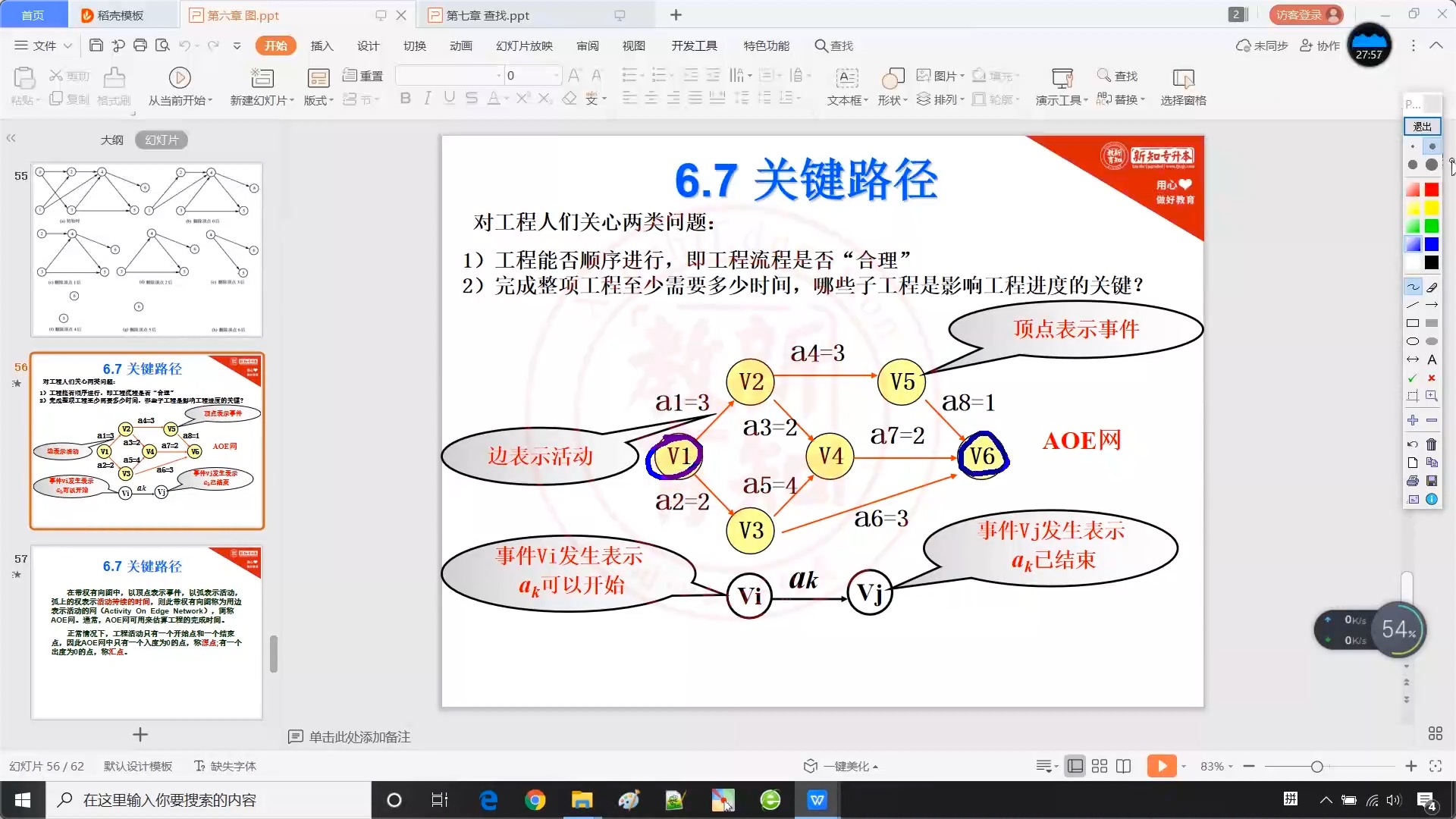
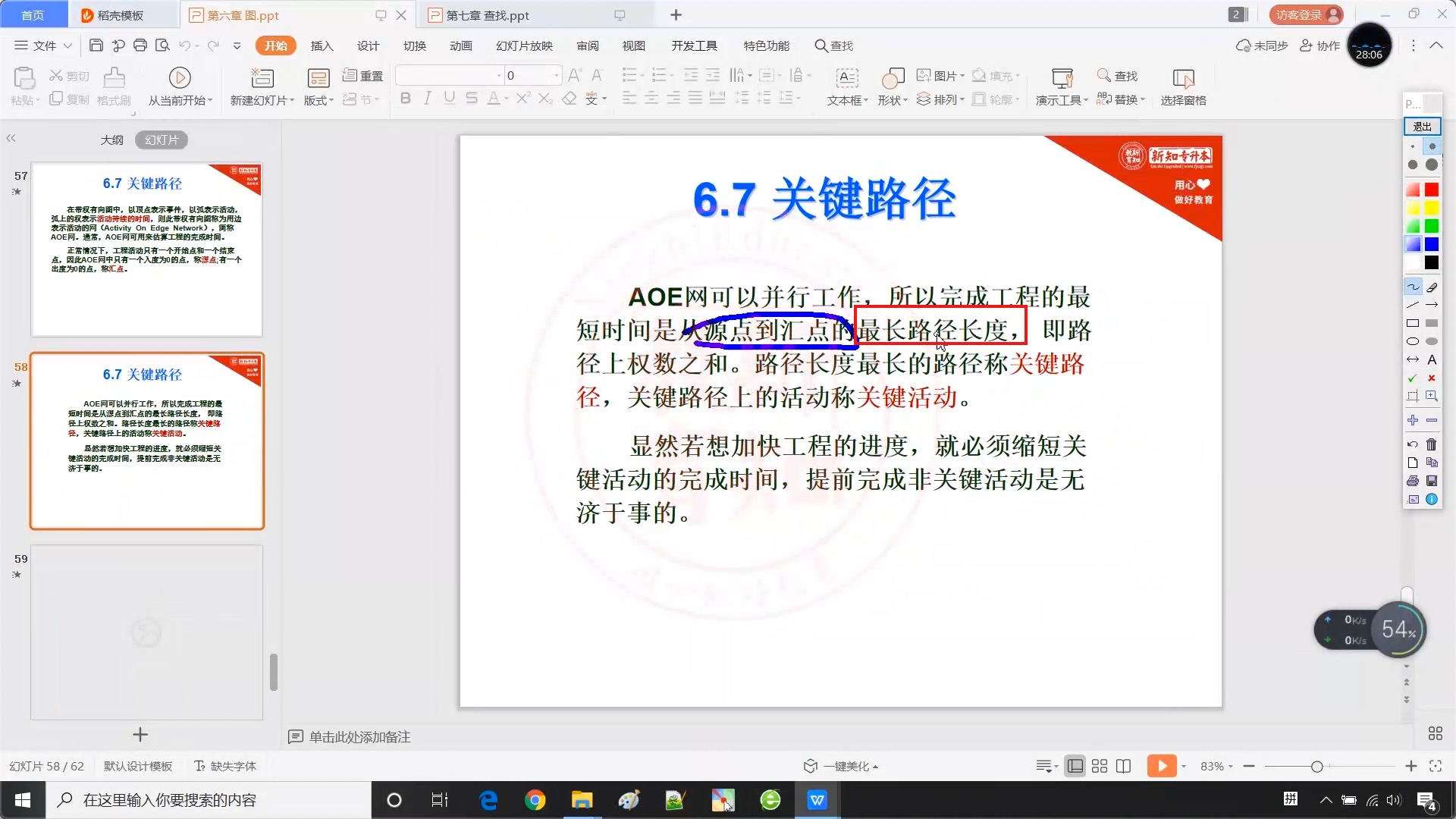
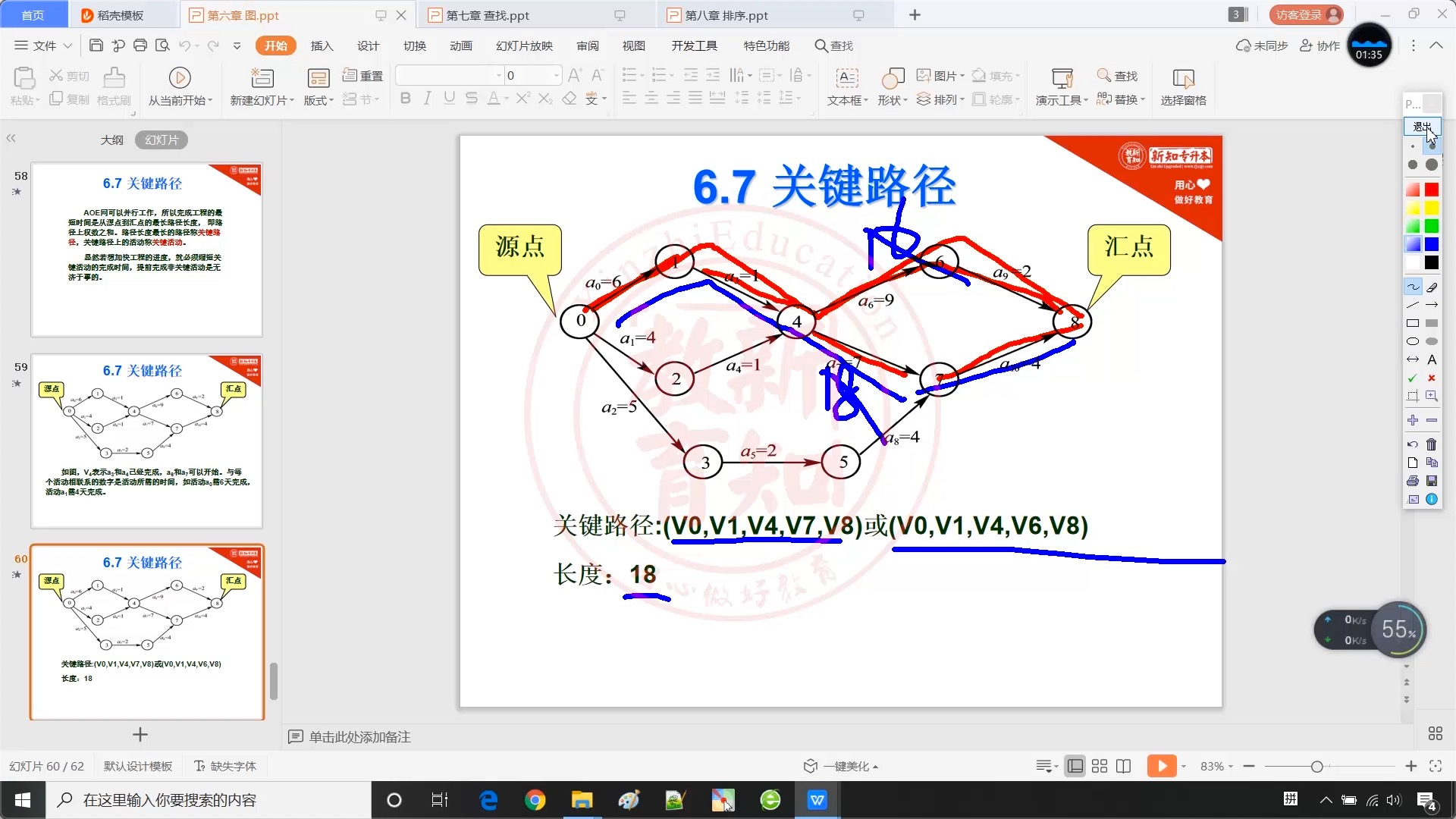
6.7 关键路径

image-20220221161104913

image-20220221161125027

image-20220221161255597

image-20220221161412439

第 7 章 - 查找

7.1 查找_基本概念

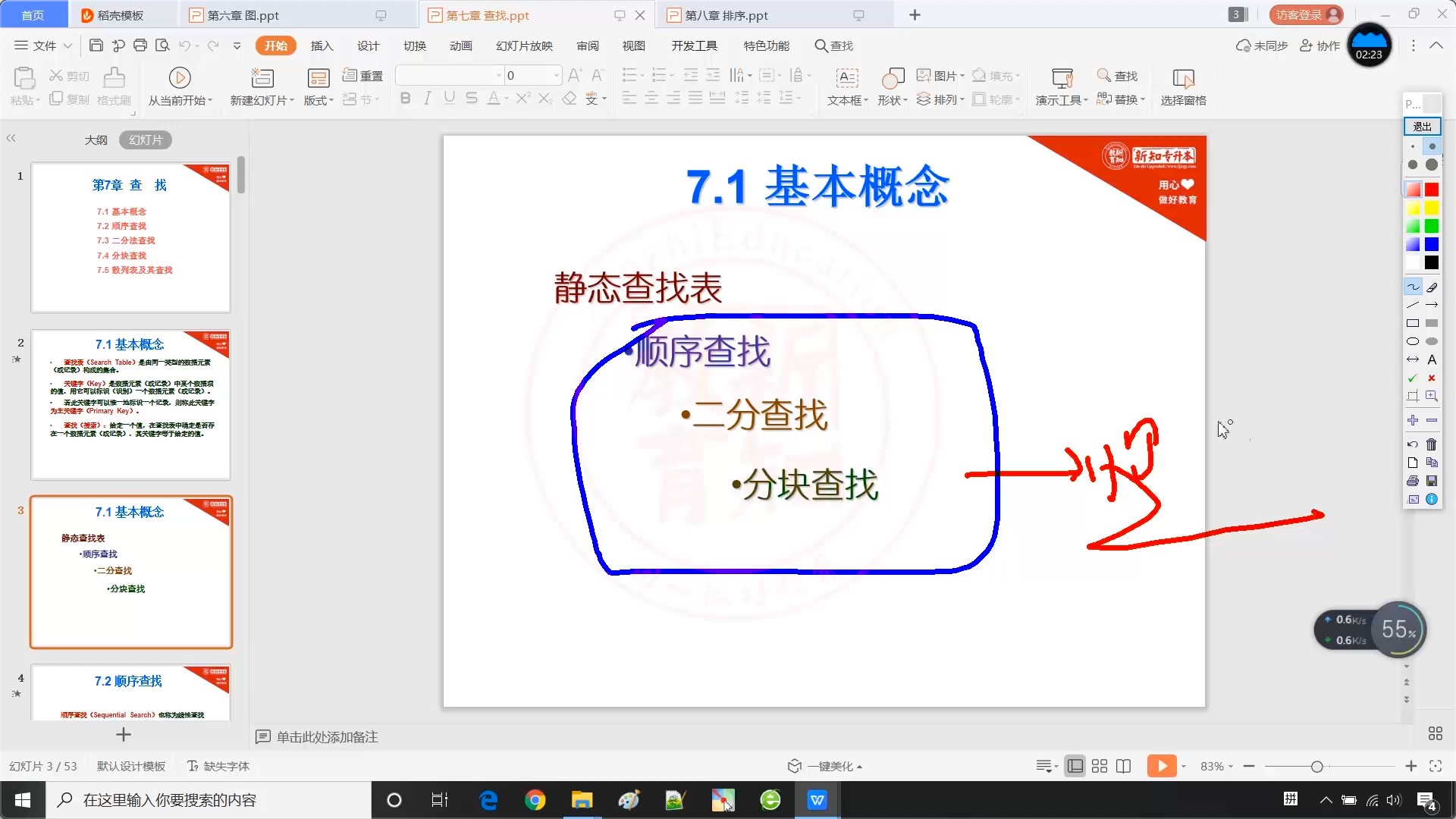
image-20220221161522592

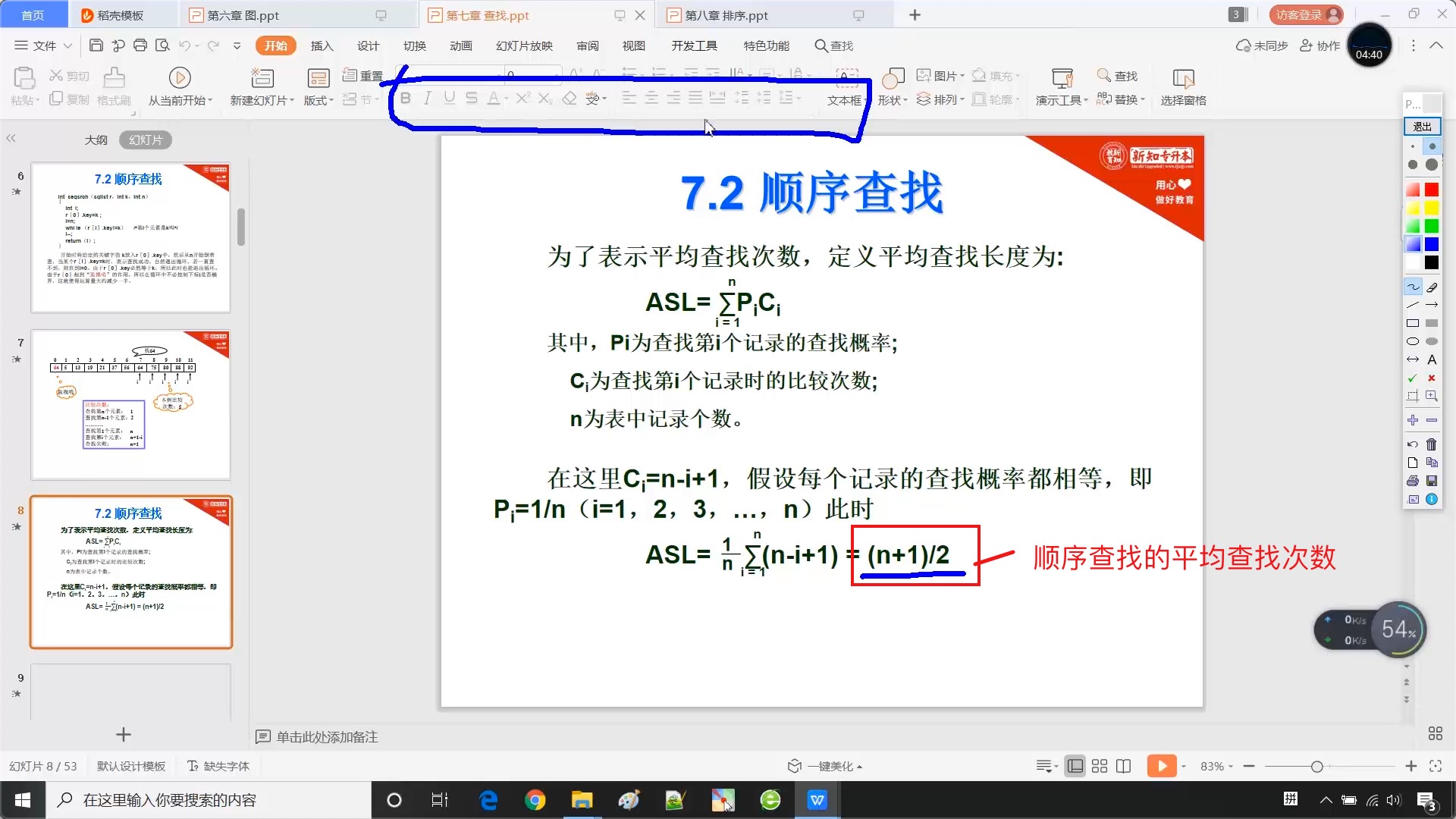
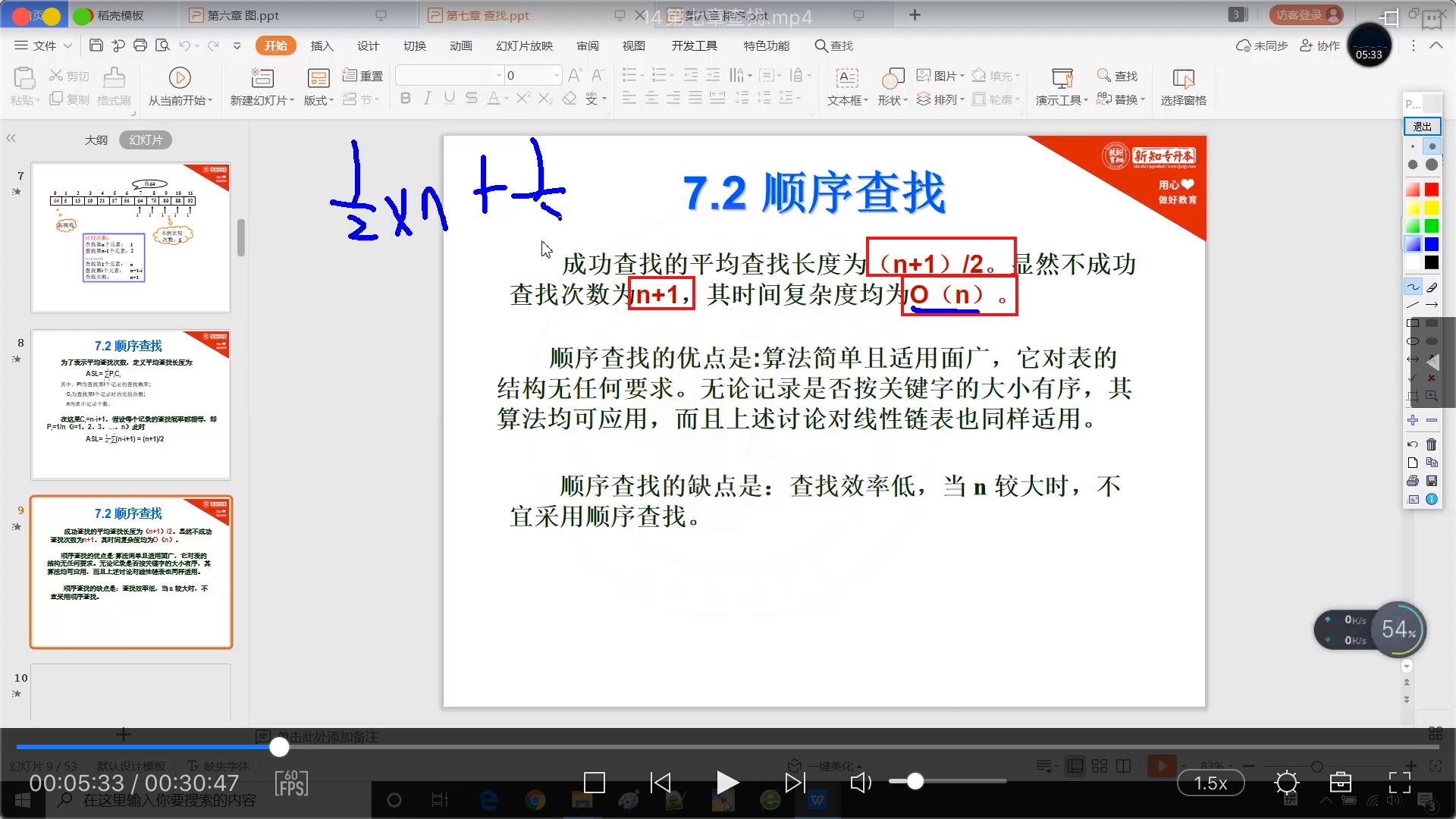
7.2 顺序查找

image-20220221161617114

image-20220221161712370

image-20220221161735351

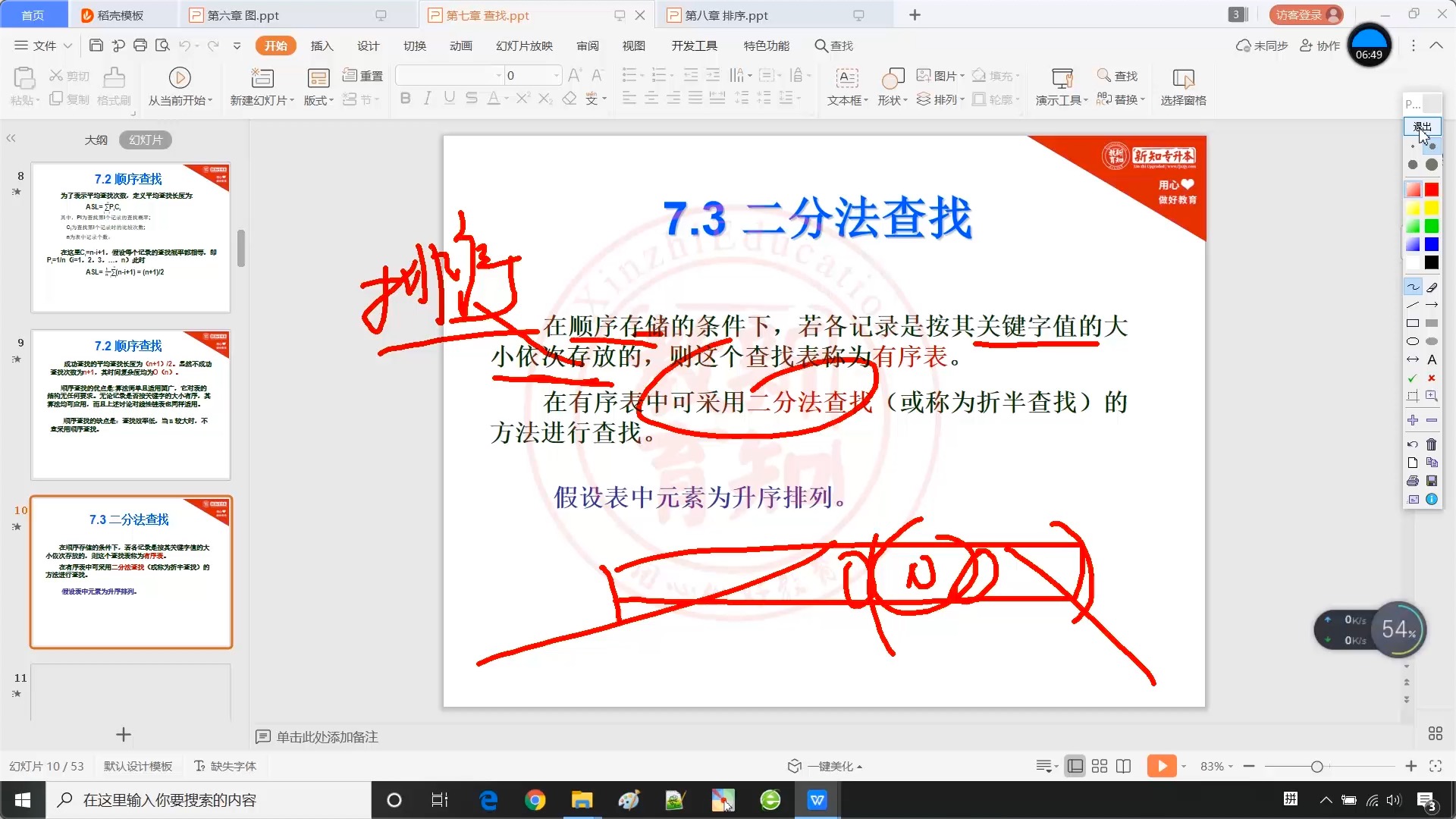
7.3 二分法查找

image-20220221161811054

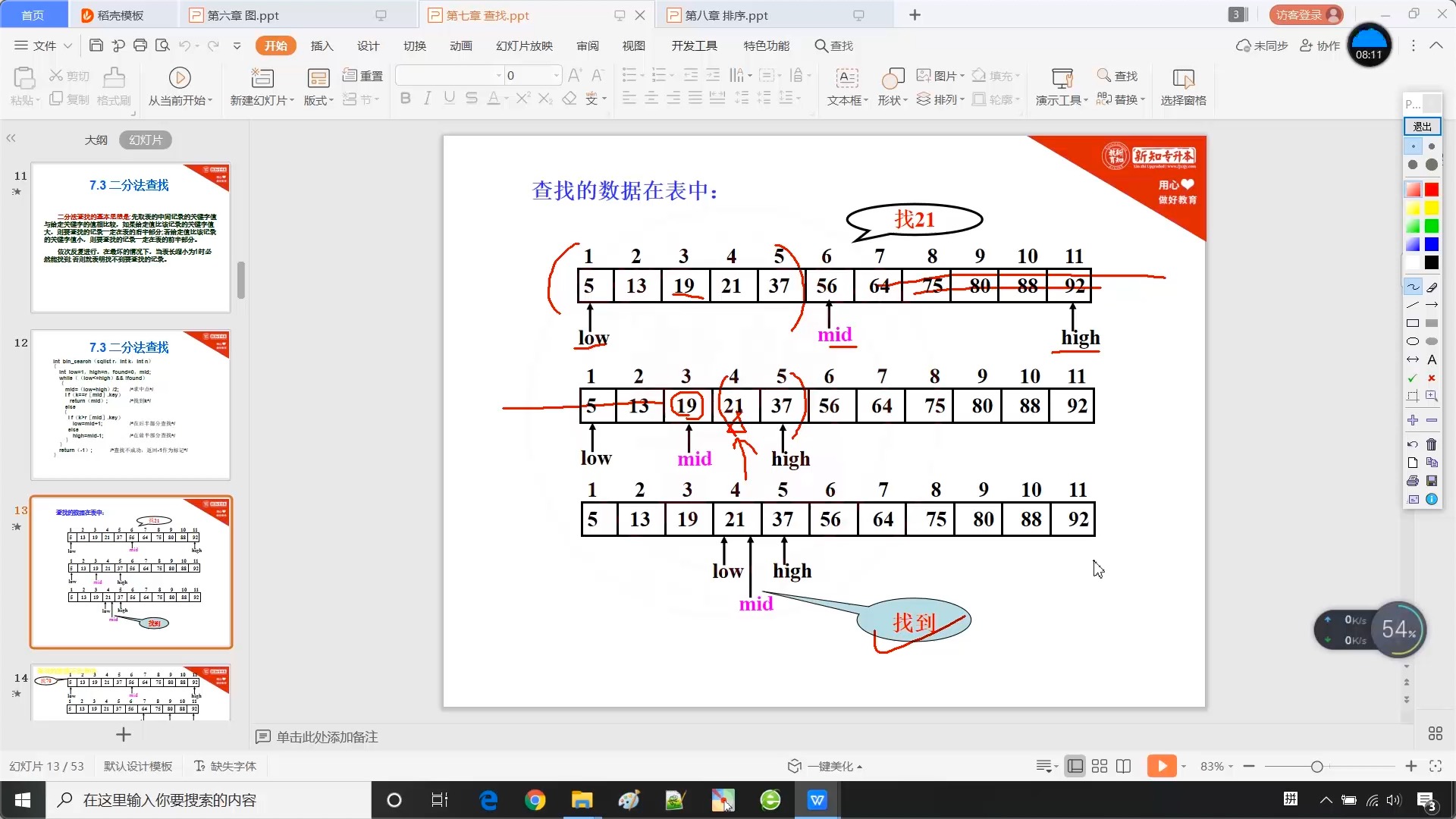
image-20220221161902626

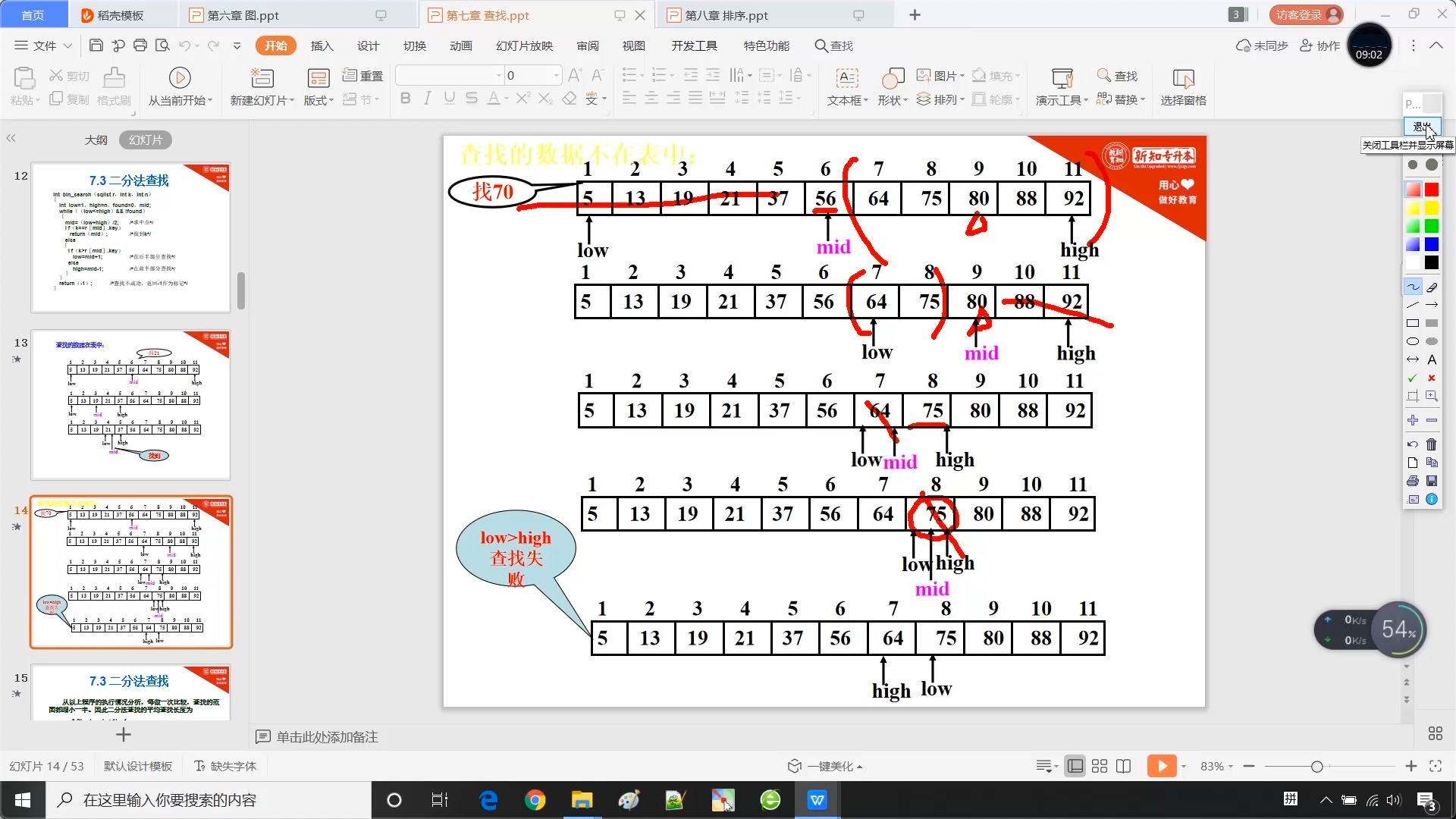
image-20220221161935167

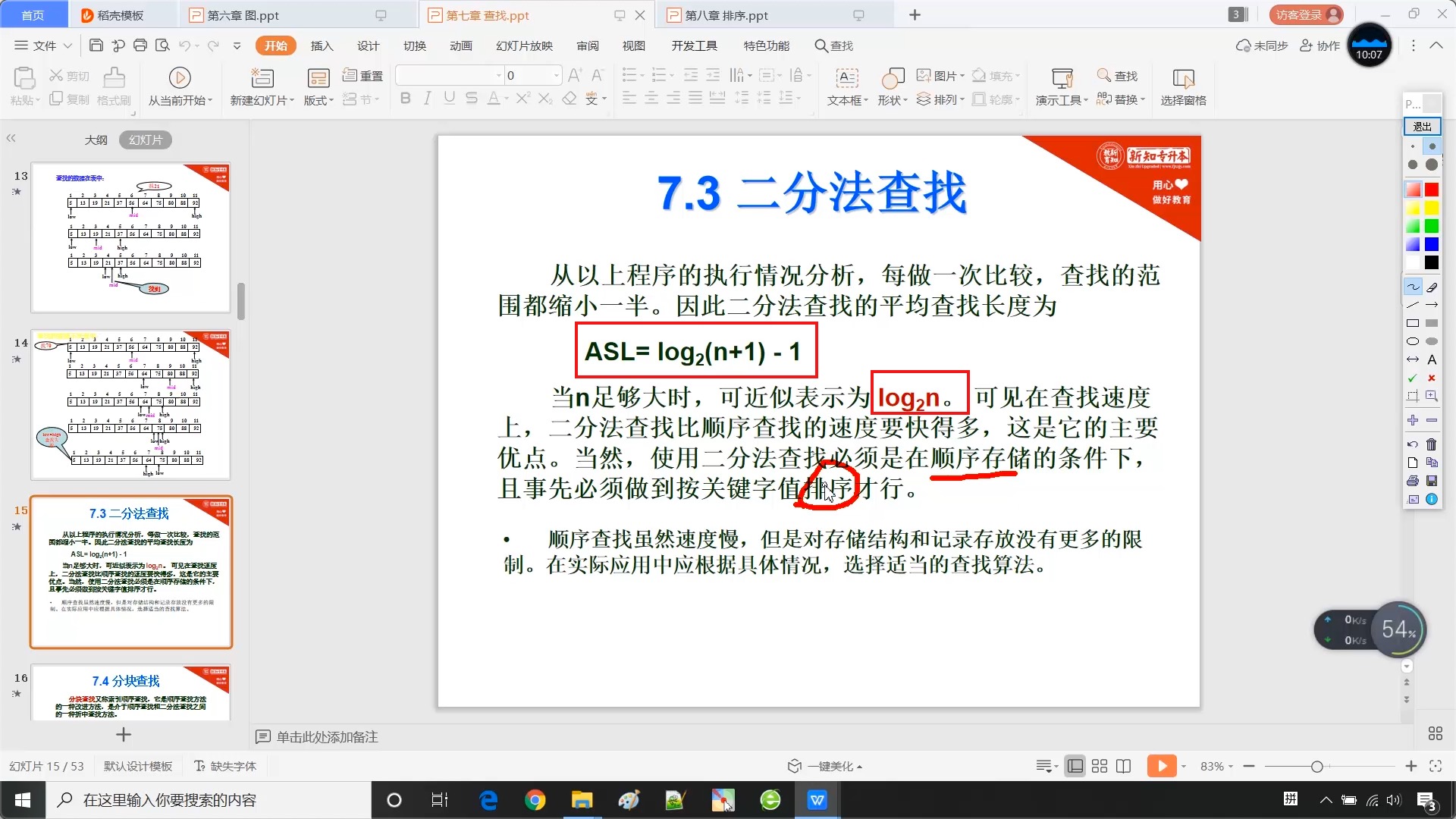
image-20220221162013547

7.4 分块查找

image-20220221162053840

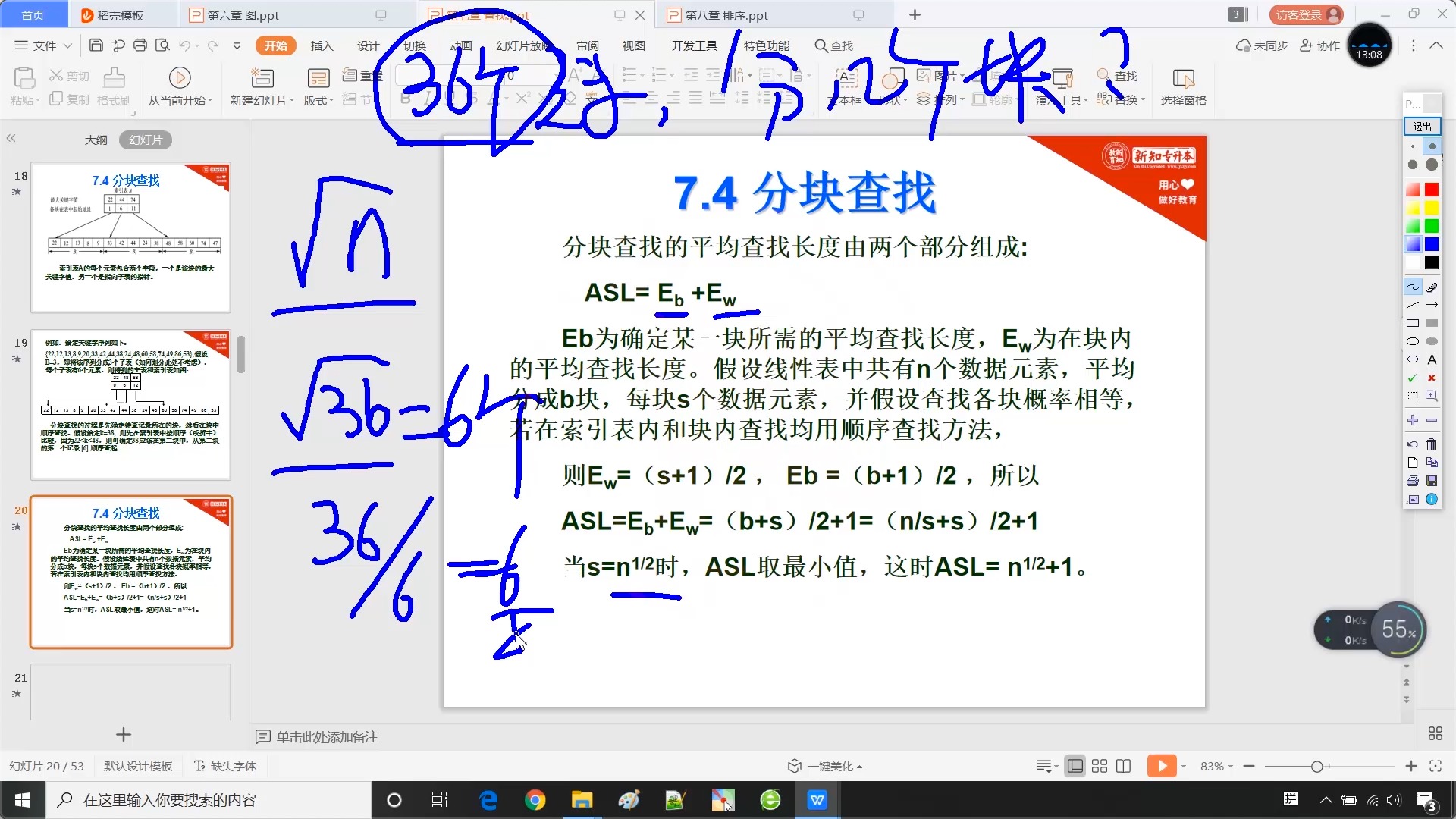
image-20220221162134147

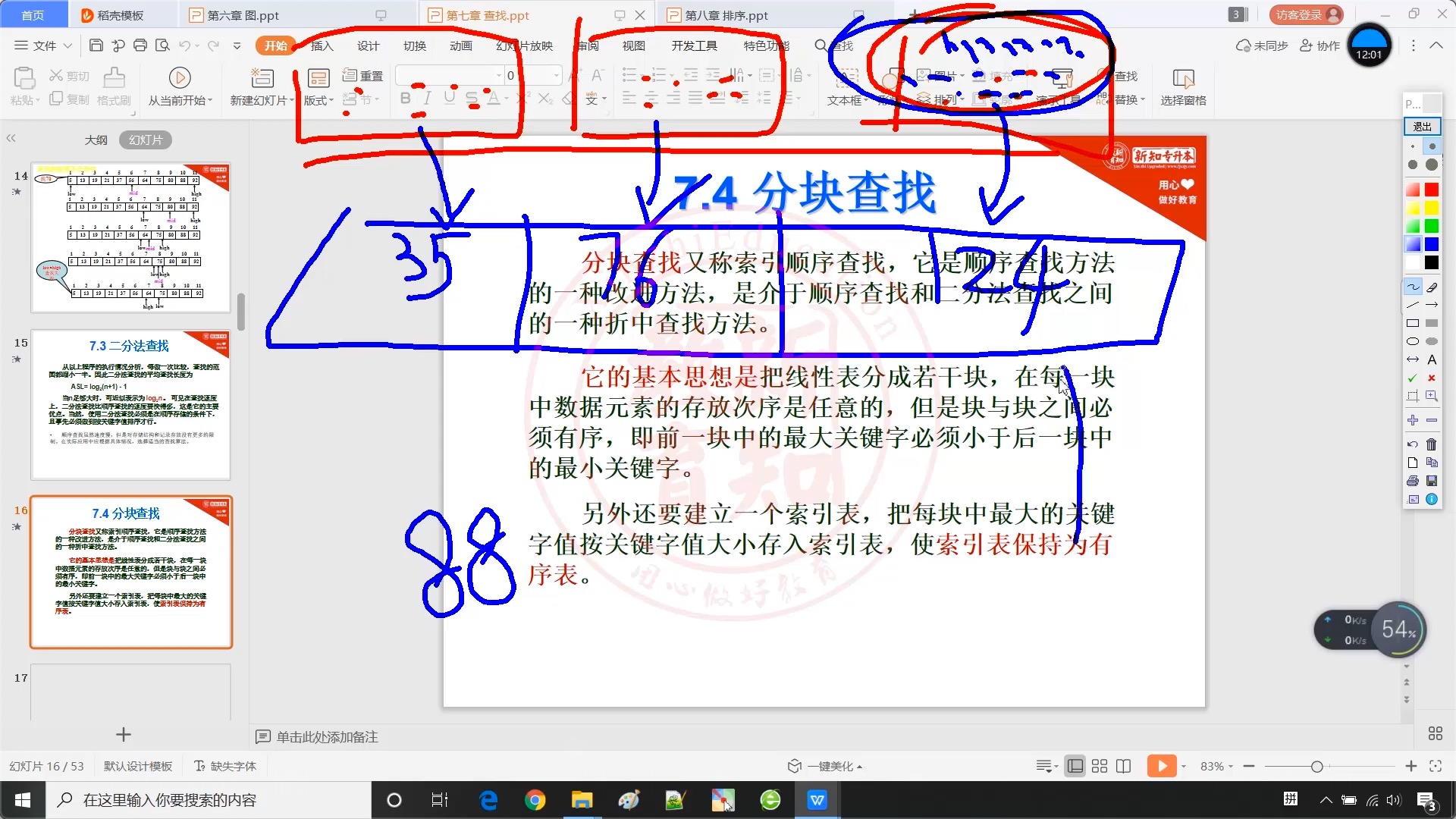
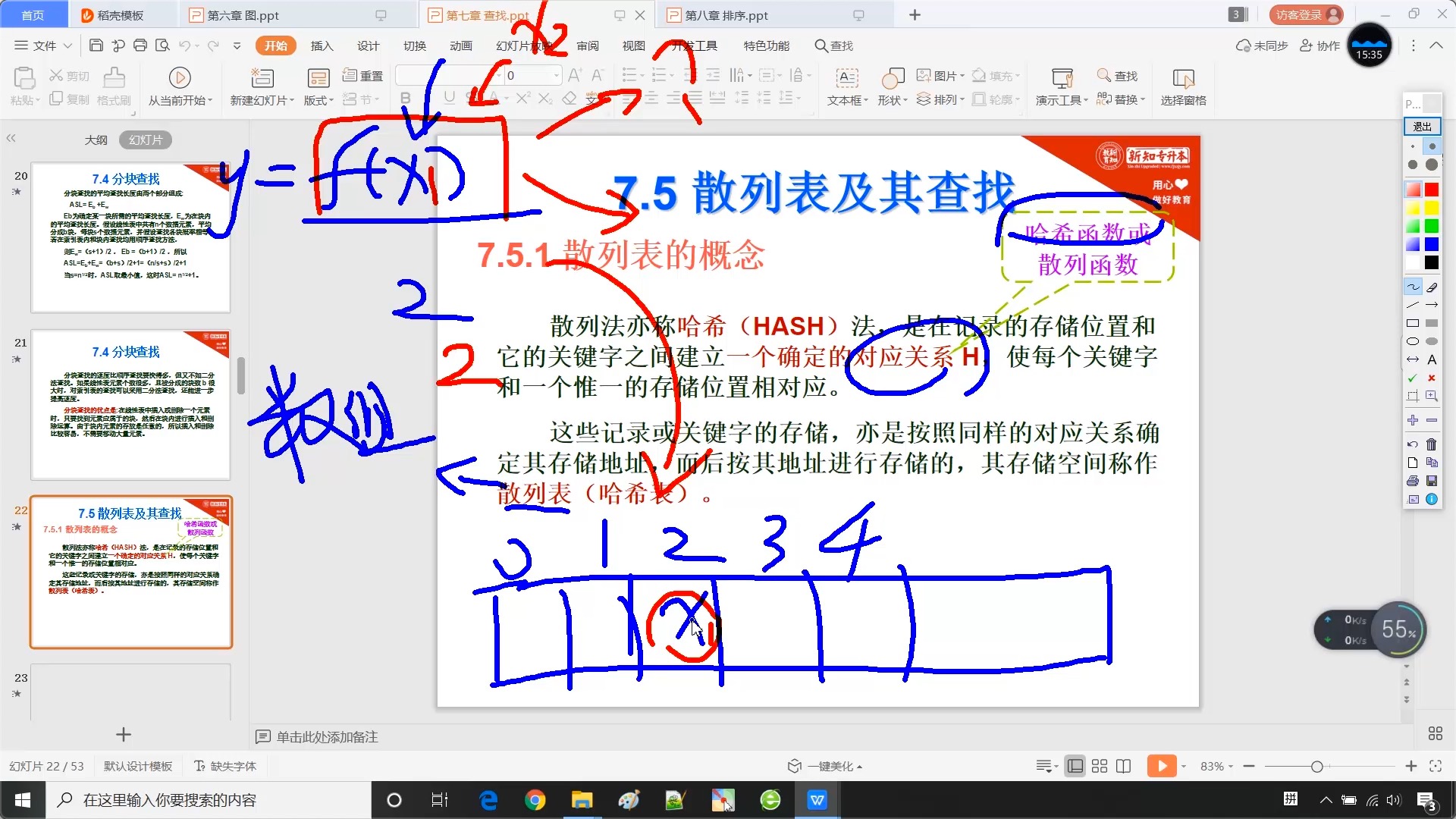
7.5 散列表及其查找【重要】

7.5.1 散列表的概念

? image-20220221162309364

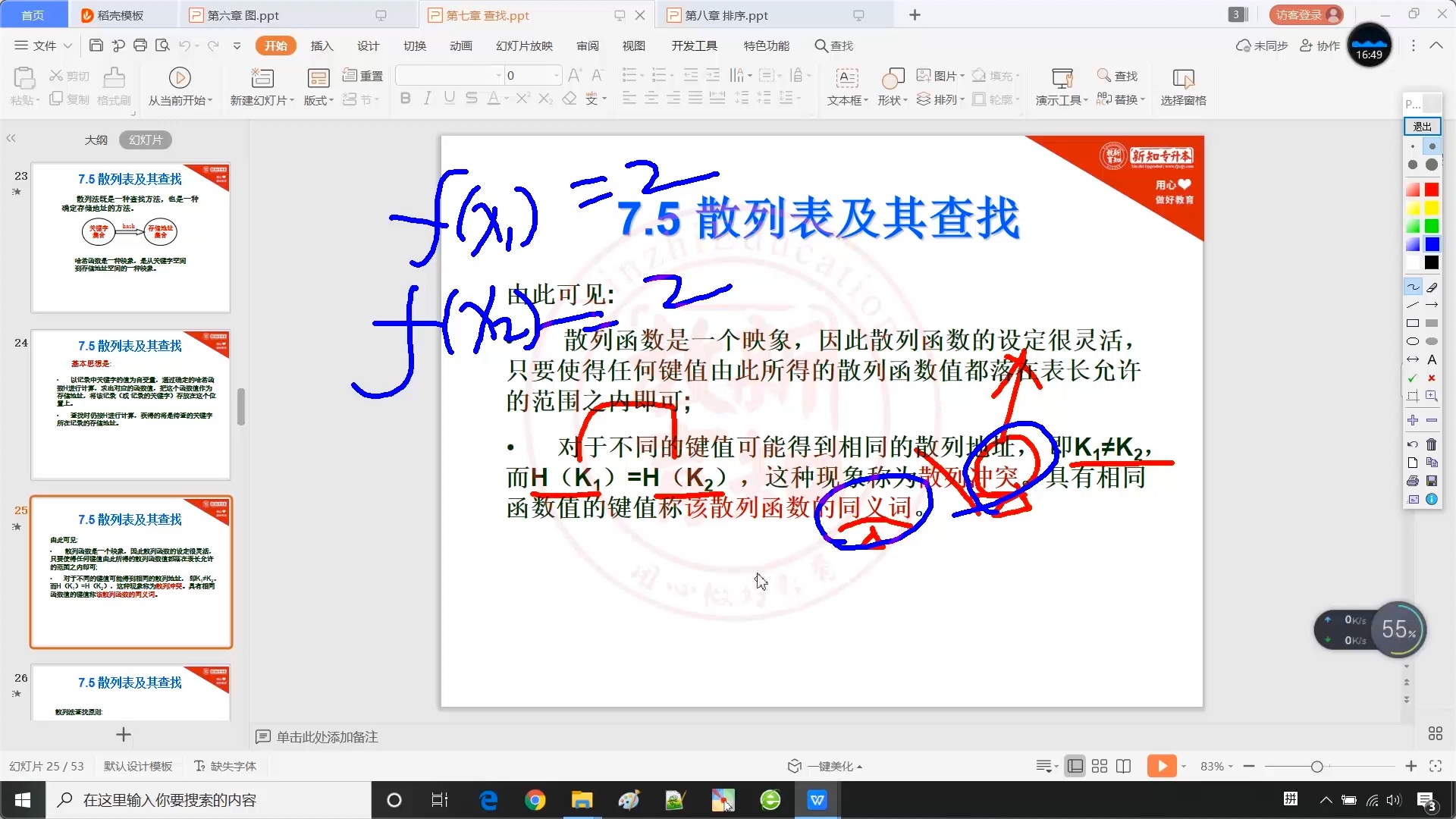
image-20220221162419907

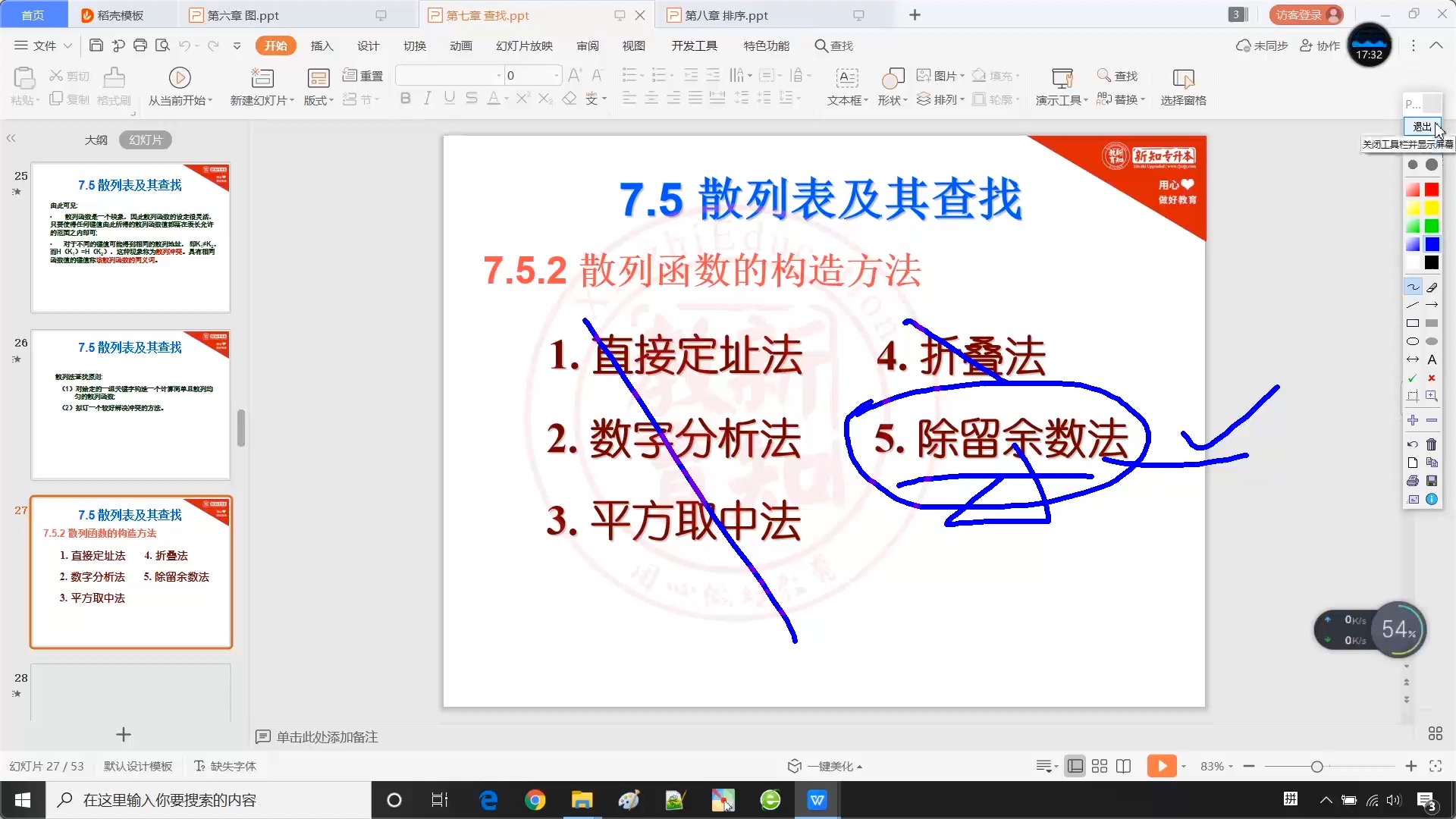
7.5.2 散列函数的构造方法

image-20220221162519101

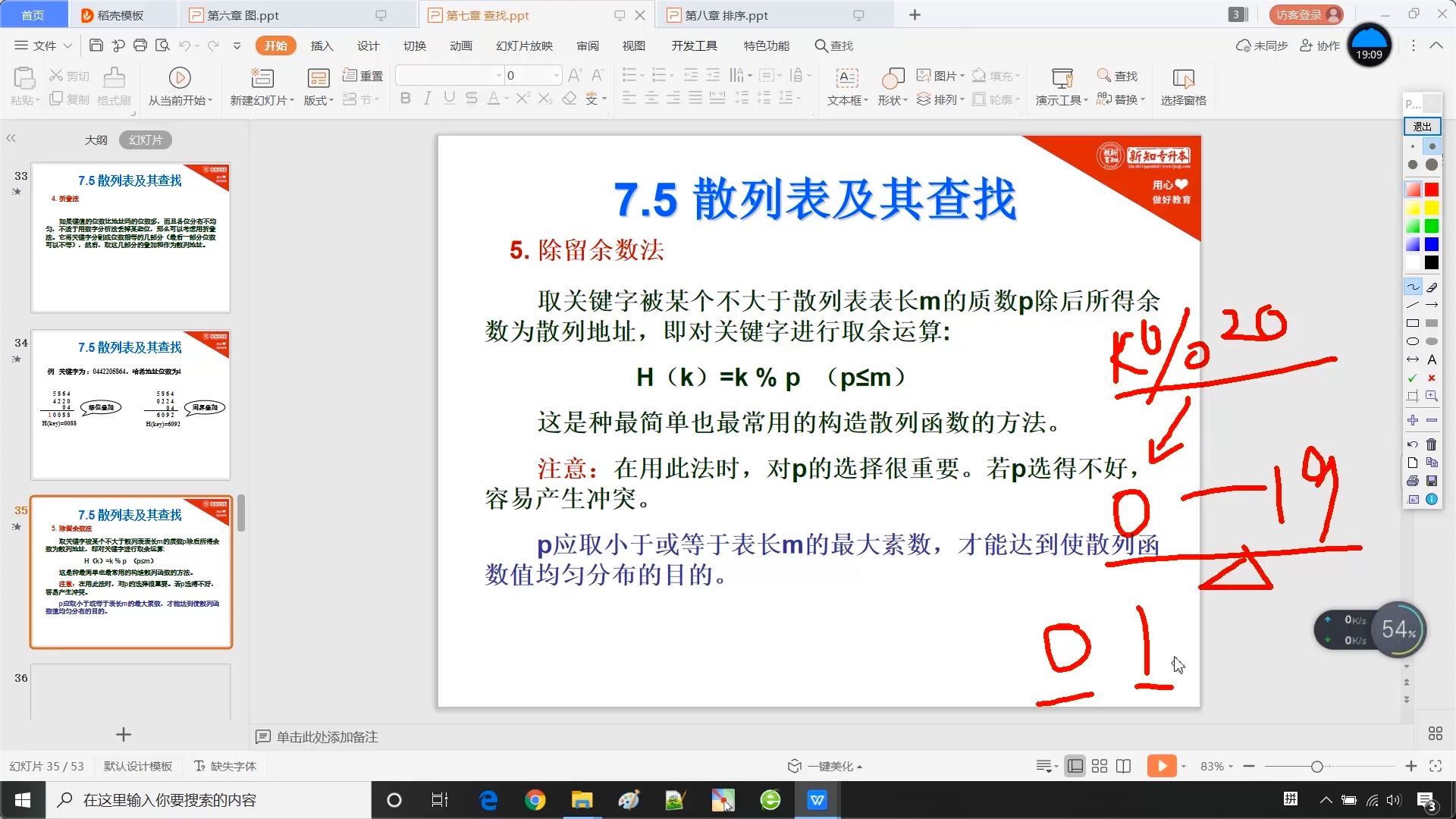
image-20220221162658764

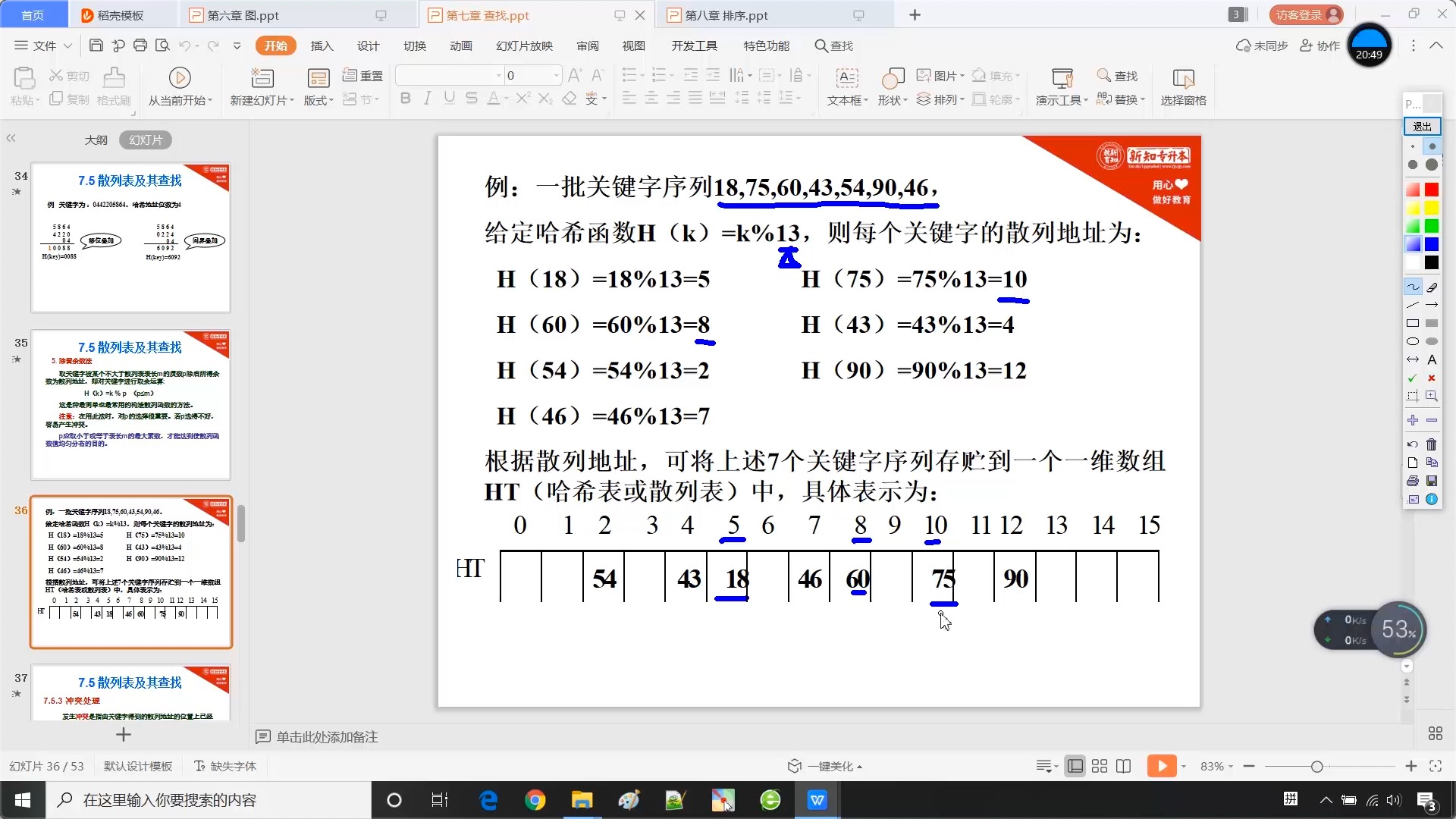
image-20220221162804079

7.5.3 线性探测法解决冲突

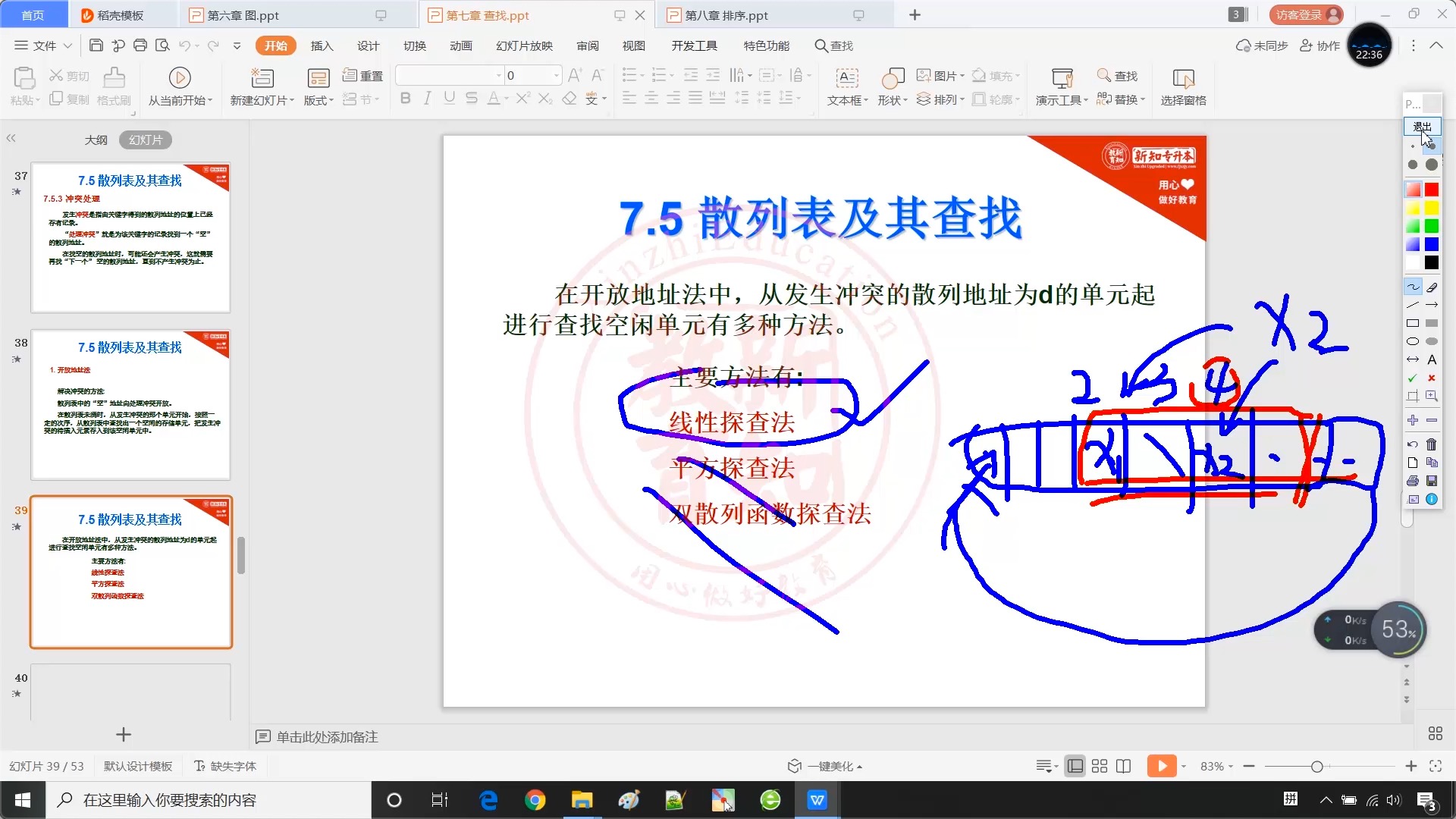
image-20220221163119098

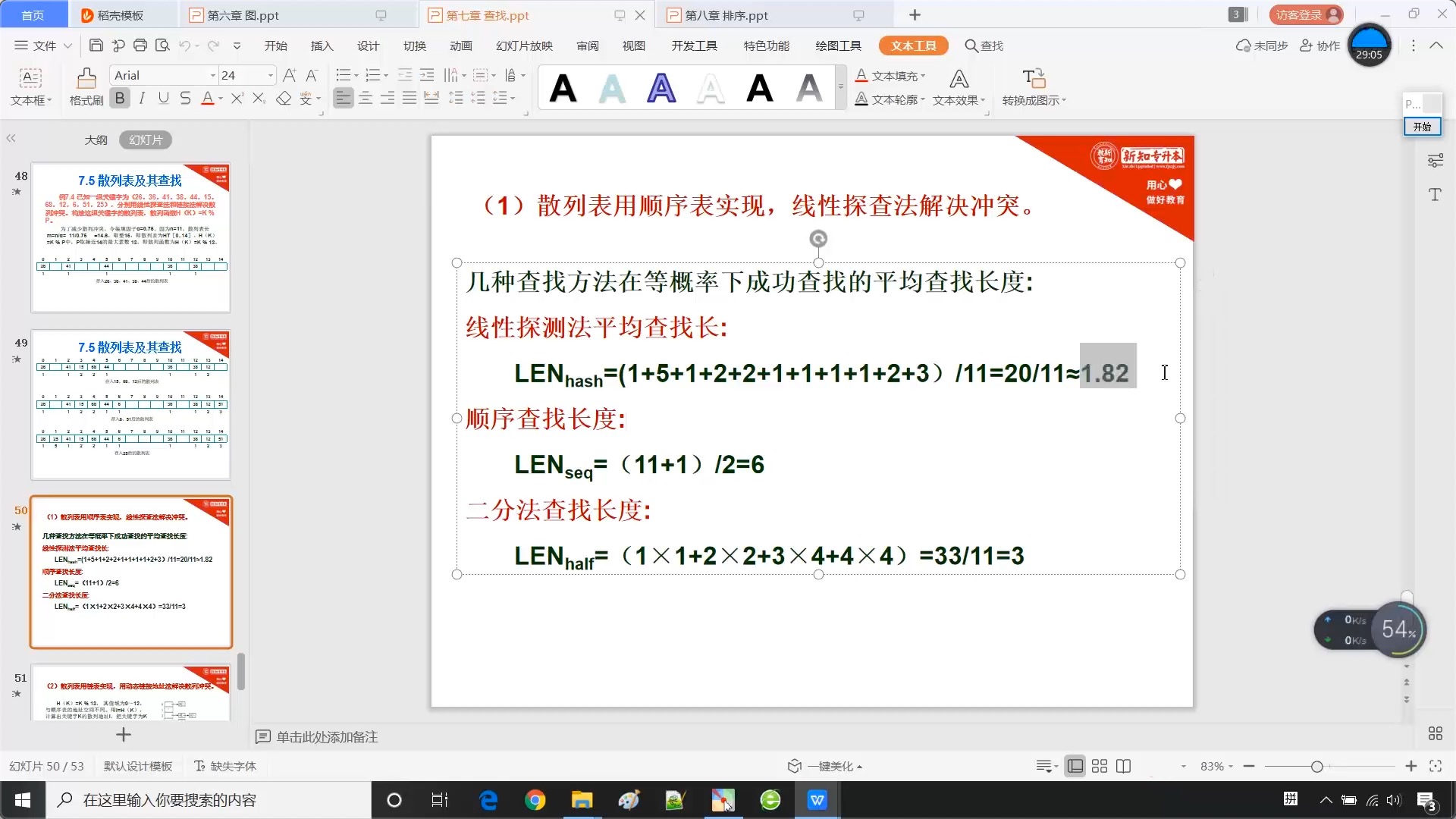
7.5.4 散列法的平均查找长度

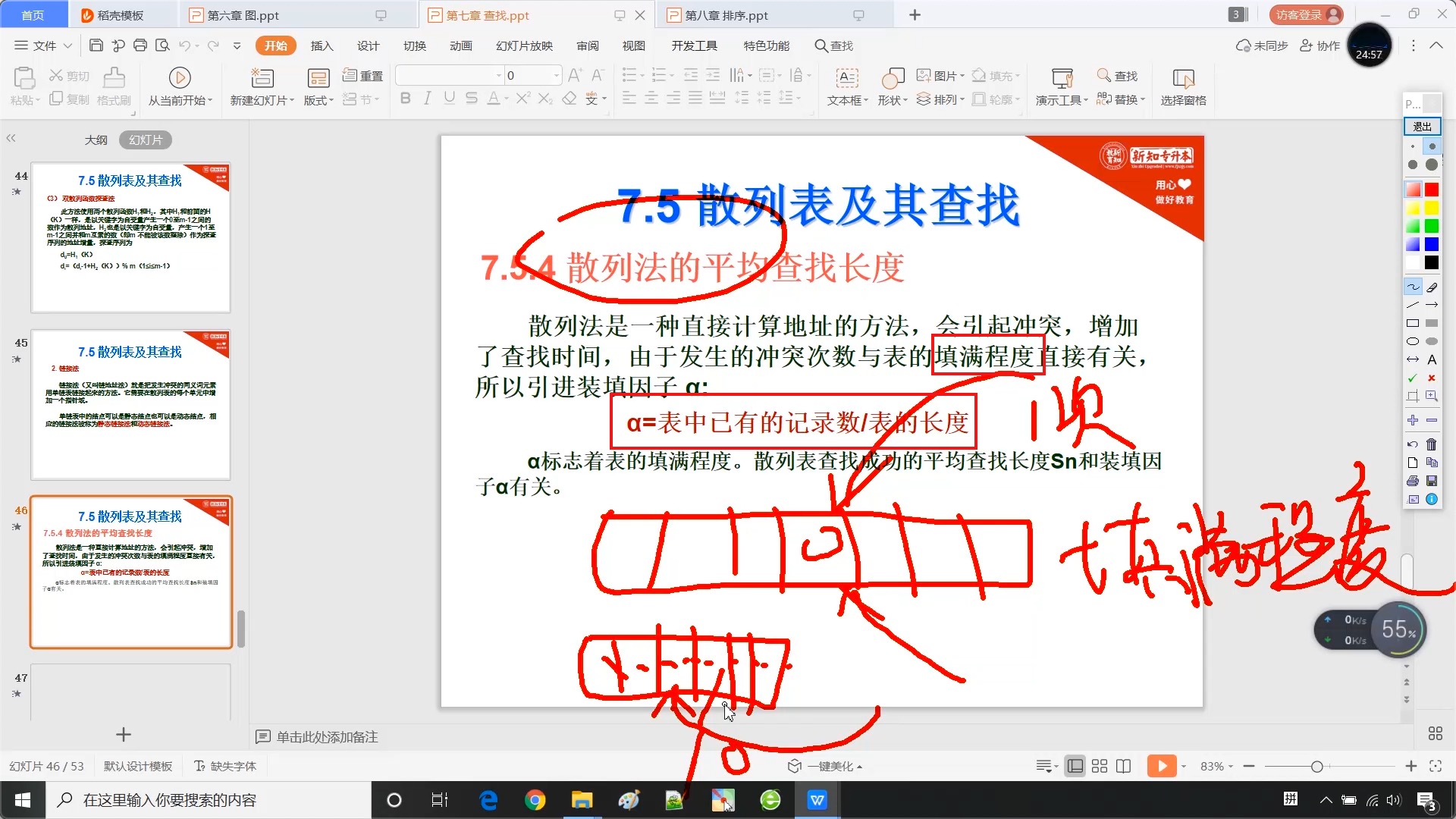
image-20220221163106806

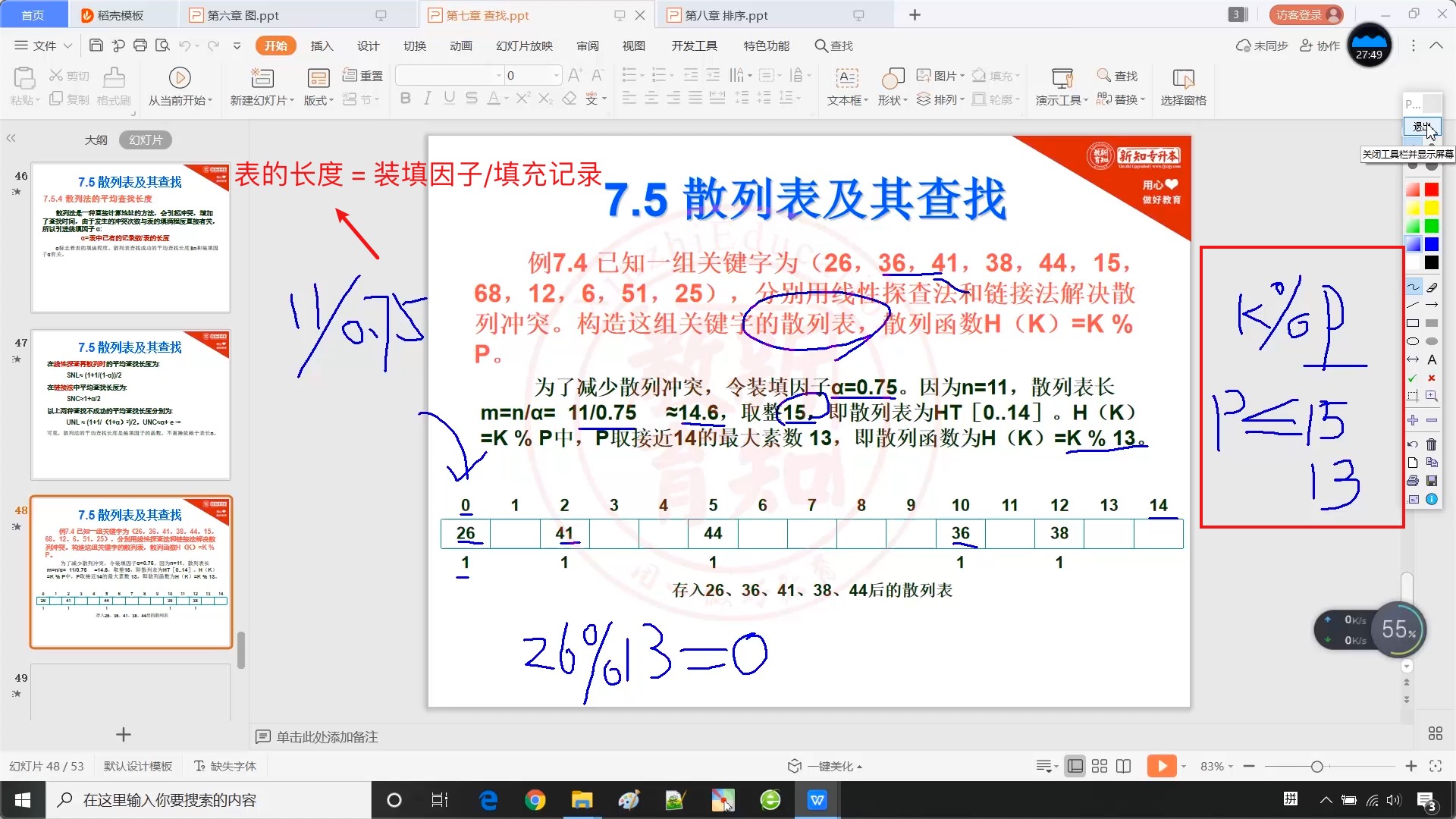
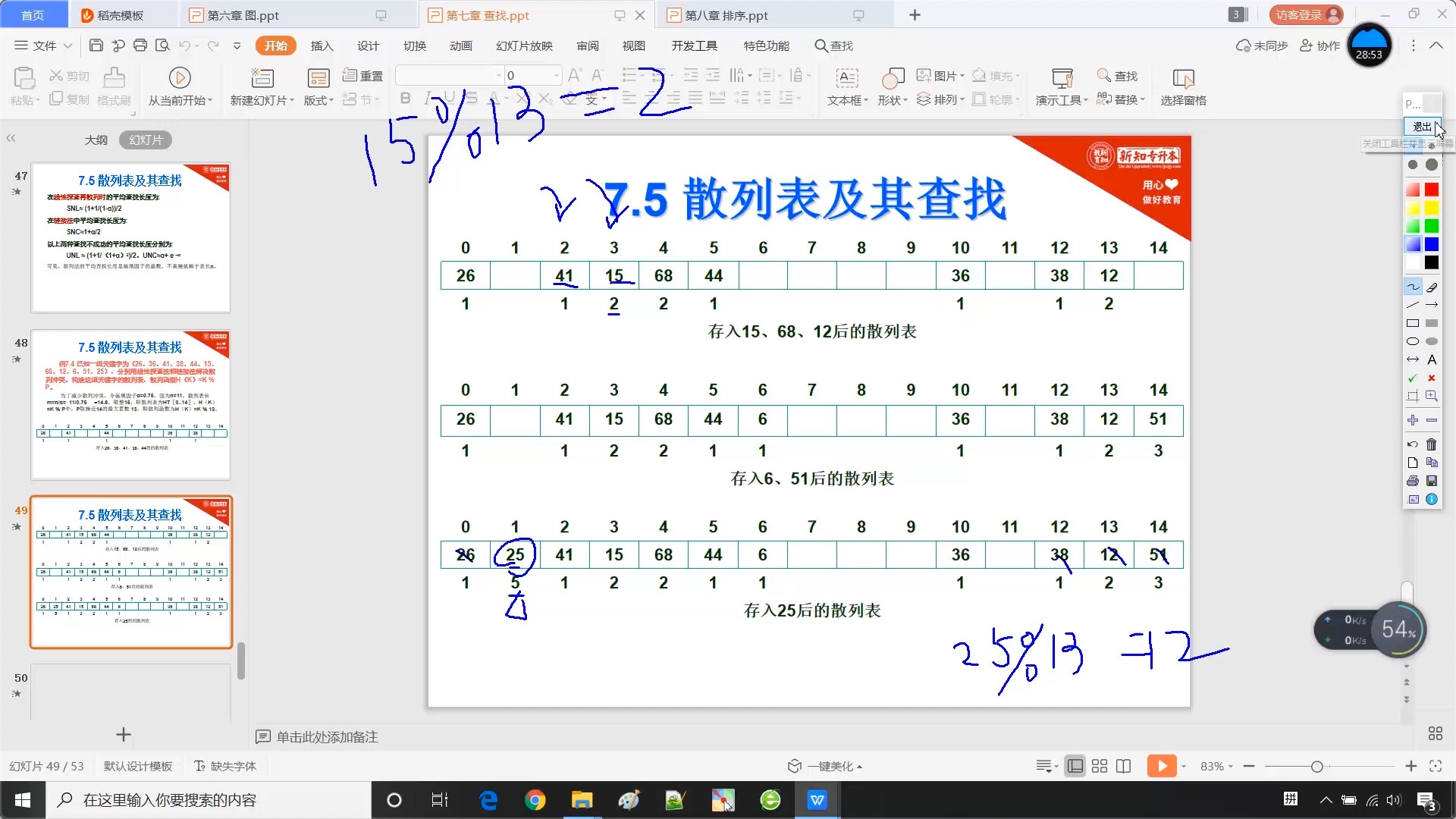
7.5.5 散列表_例题

? image-20220221163544389

image-20220221163705864

image-20220221163737690

第 8 章 - 排序

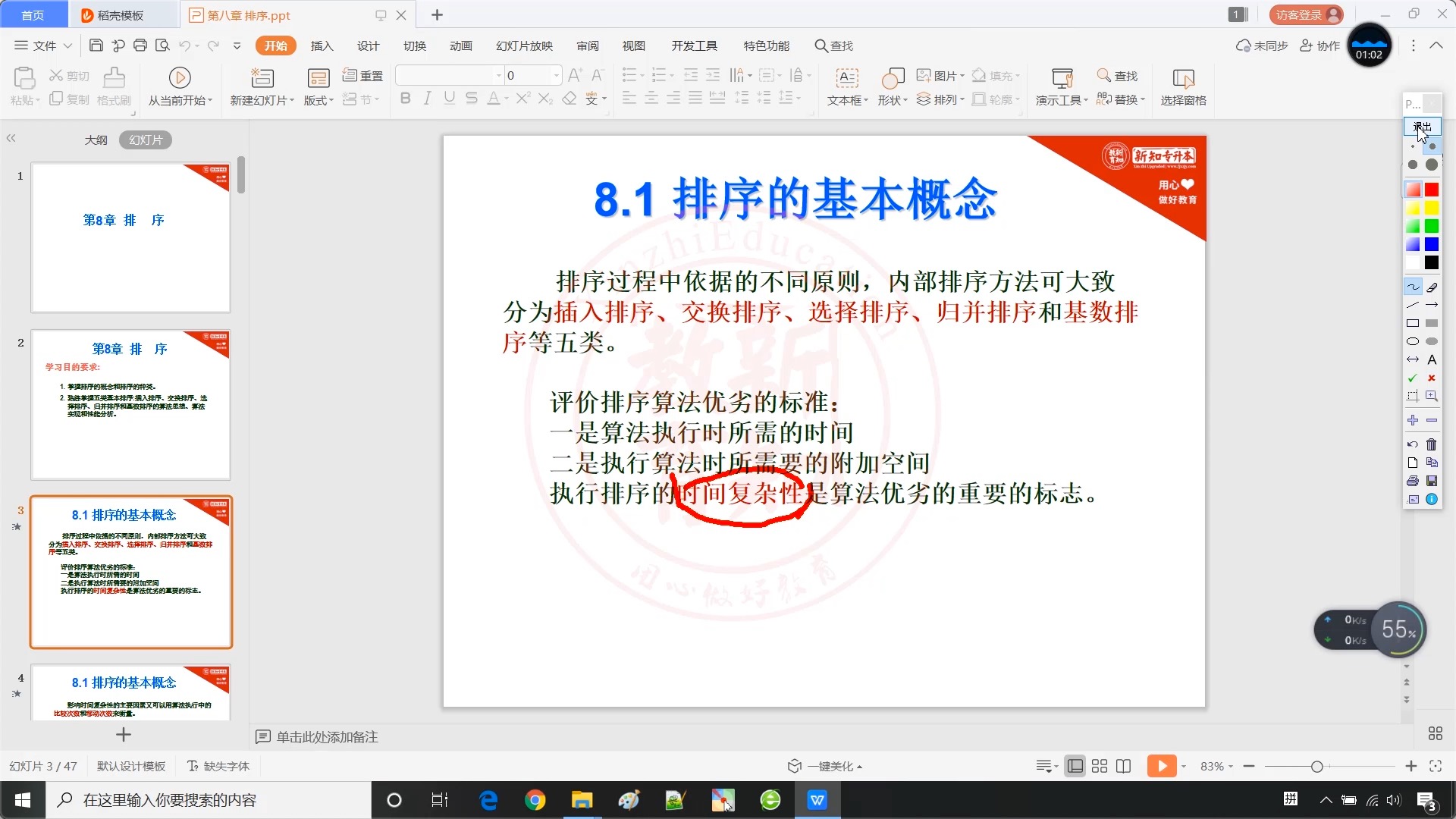
8.1 排序的基本概念

image-20220221163945318

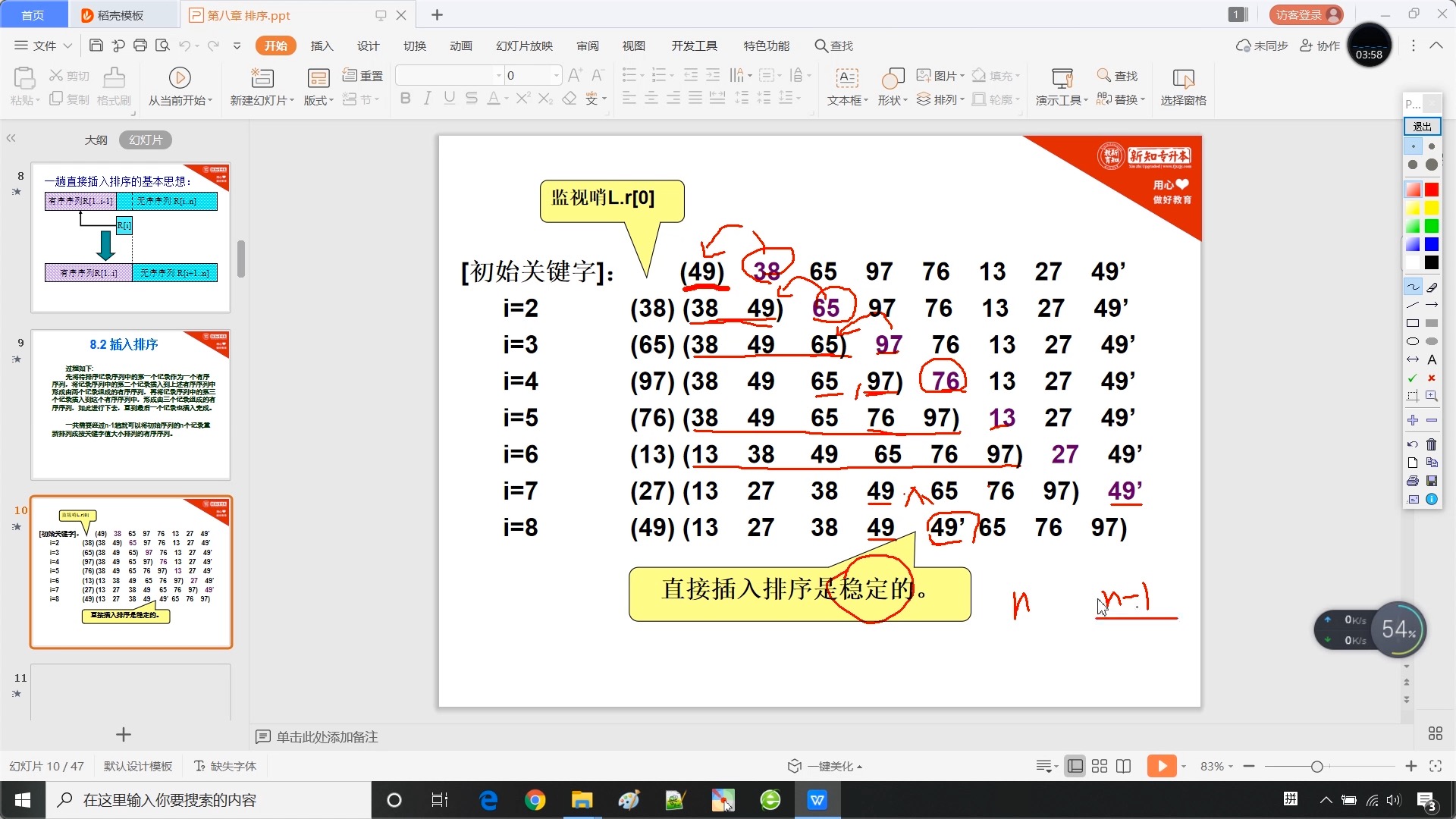
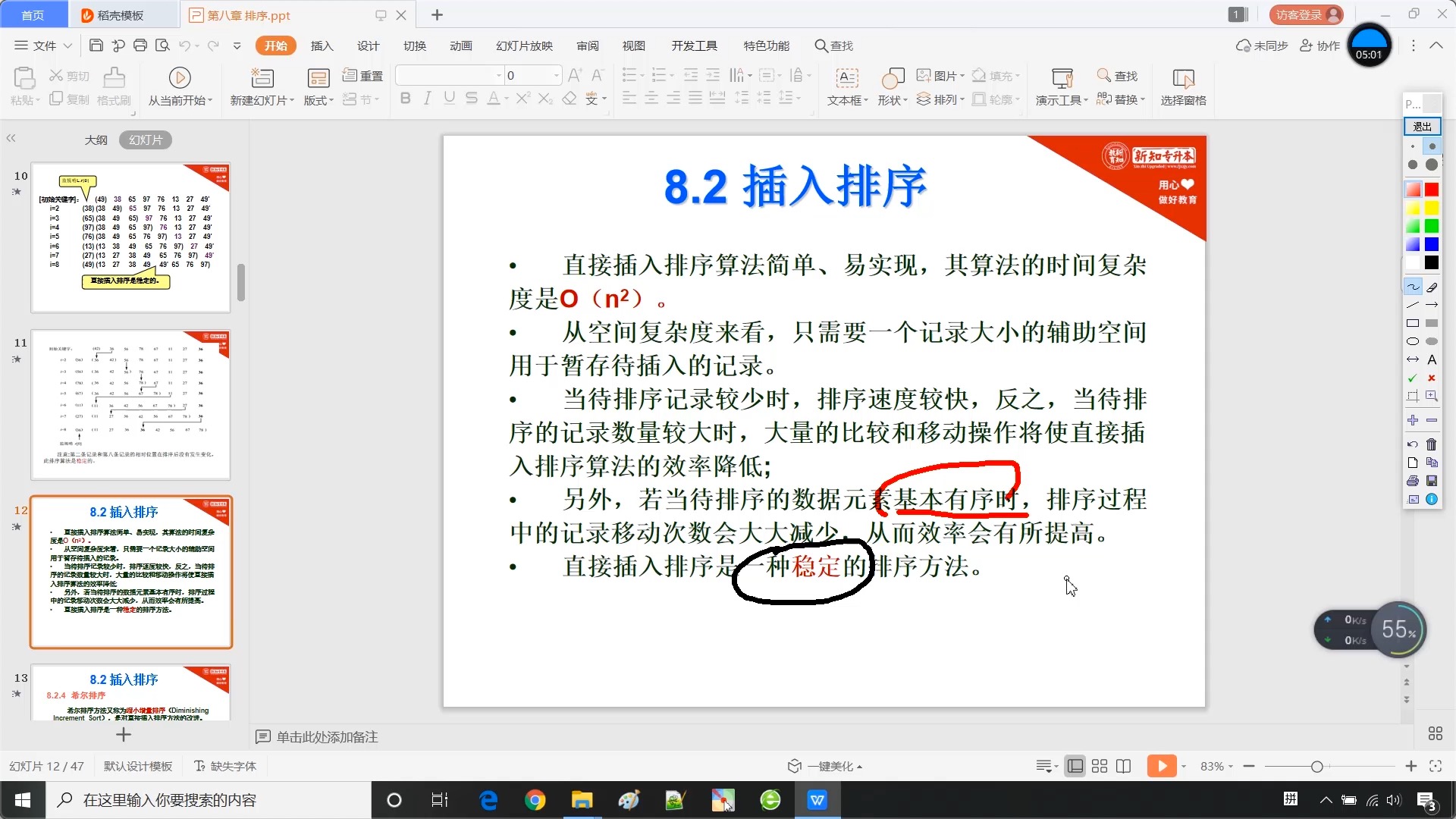
8.2 插入排序 - 直接插入

image-20220221164108928

image-20220221164244770

image-20220221164333989

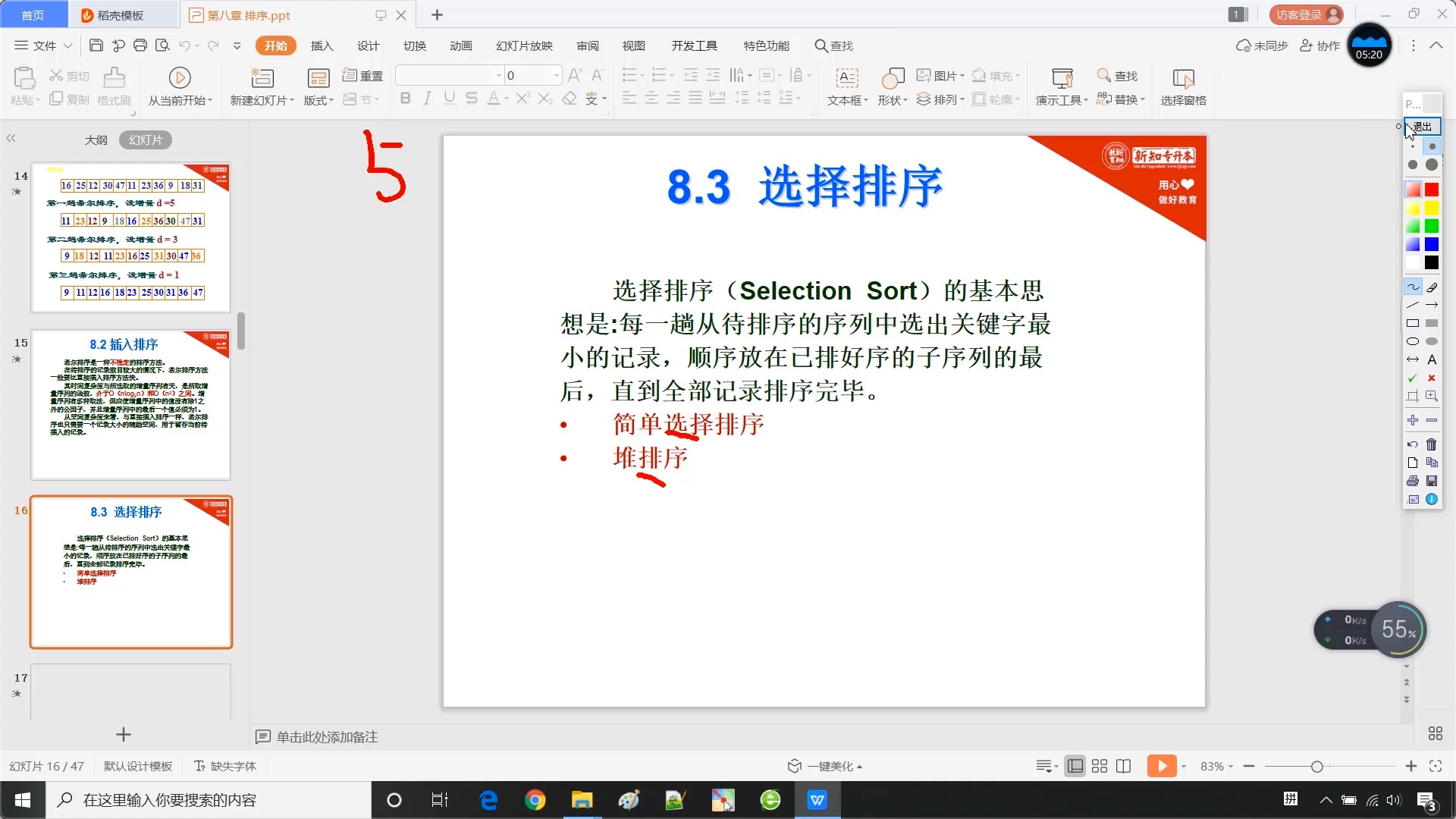
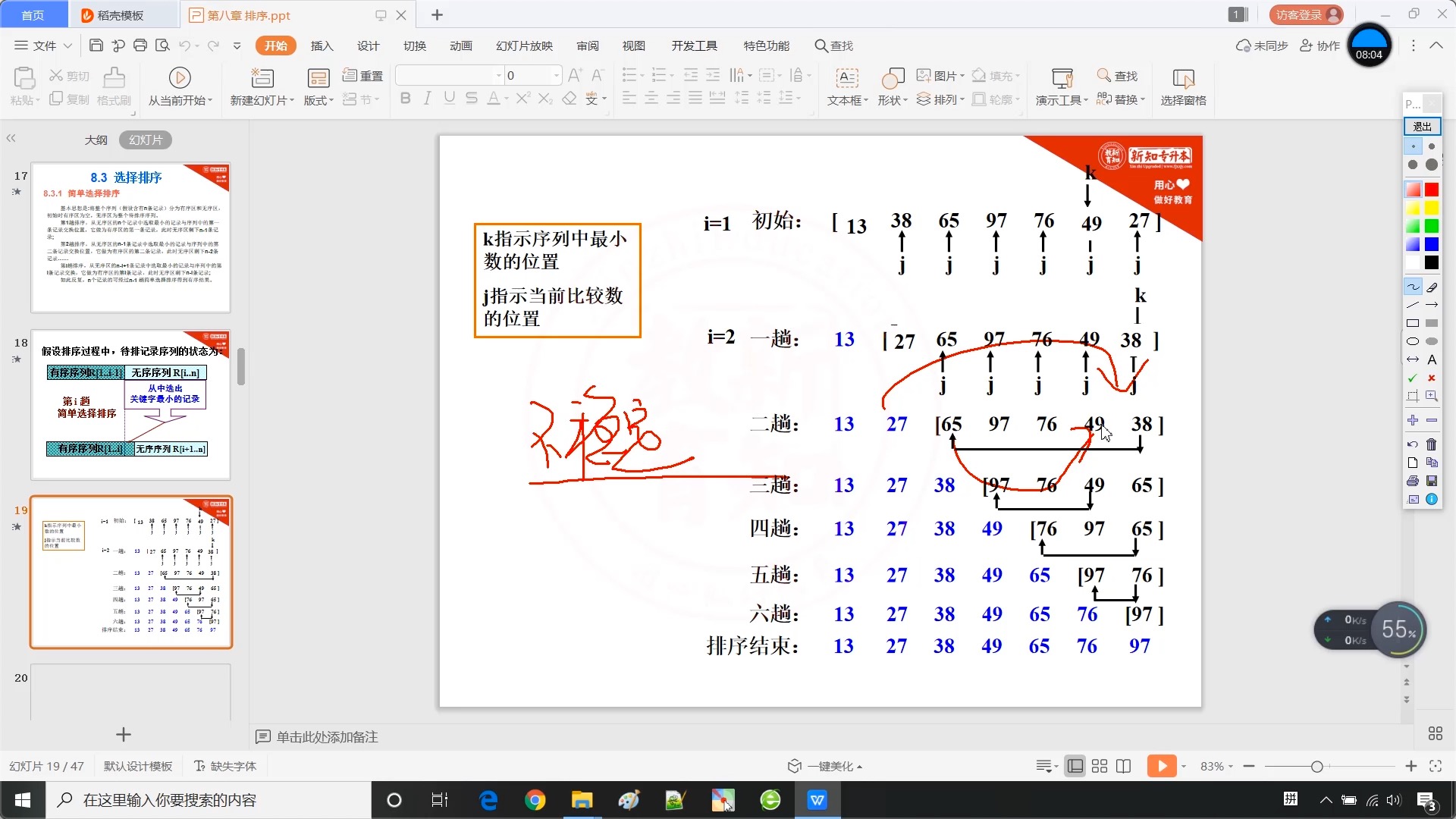
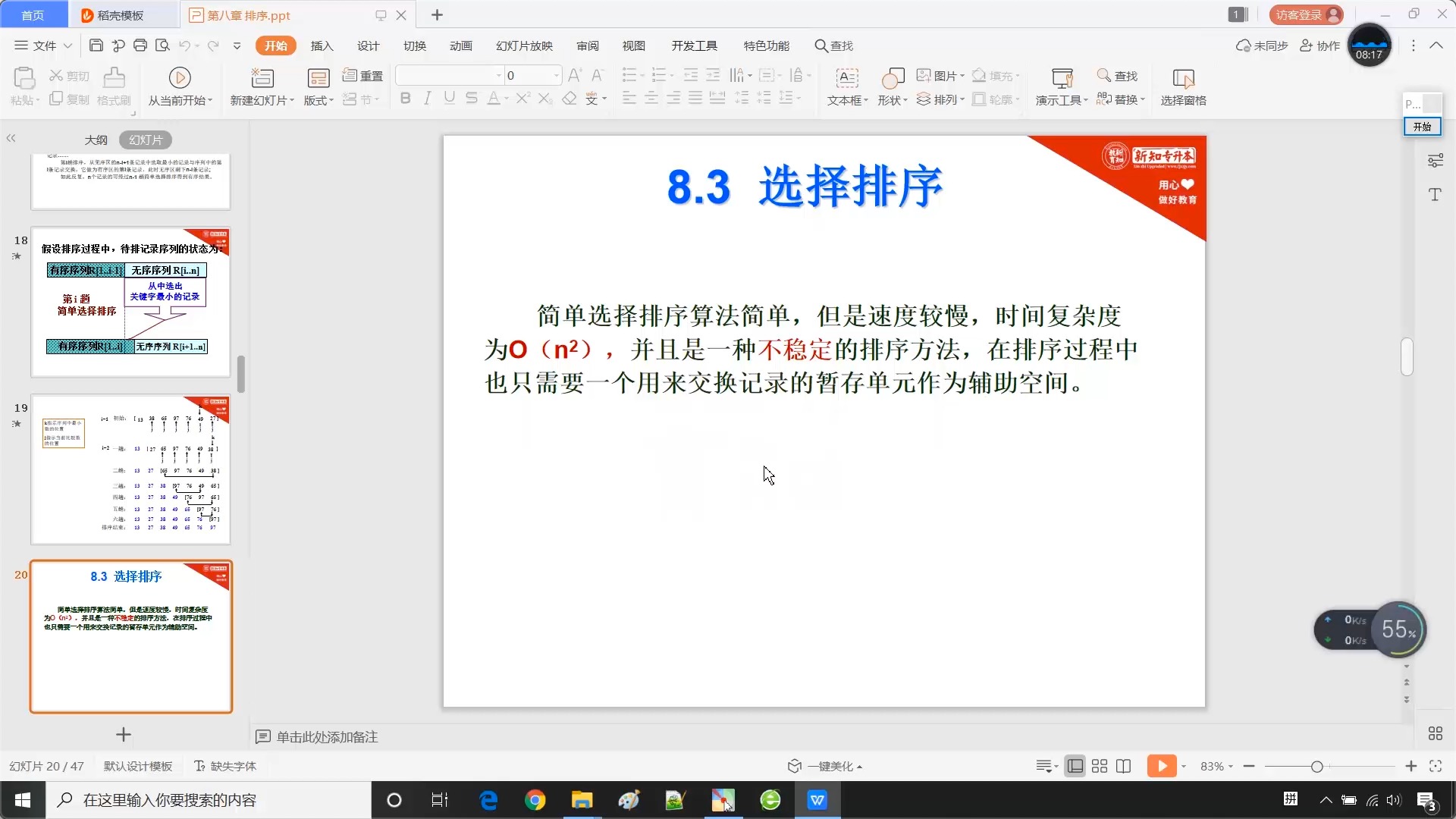
8.3 选择排序 - 简单选择排序

image-20220221164406414

?

image-20220221164745920

image-20220221164801250

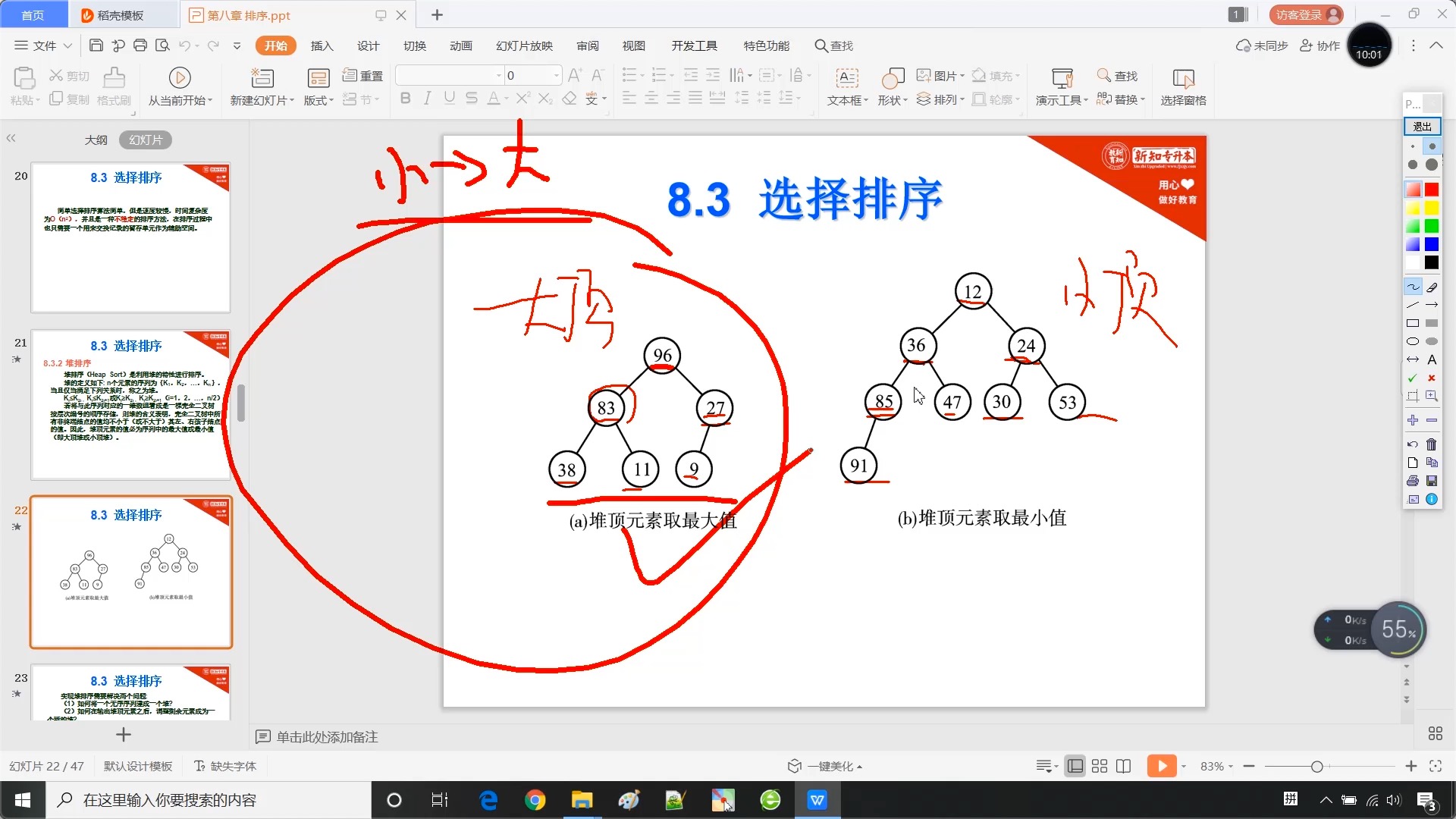
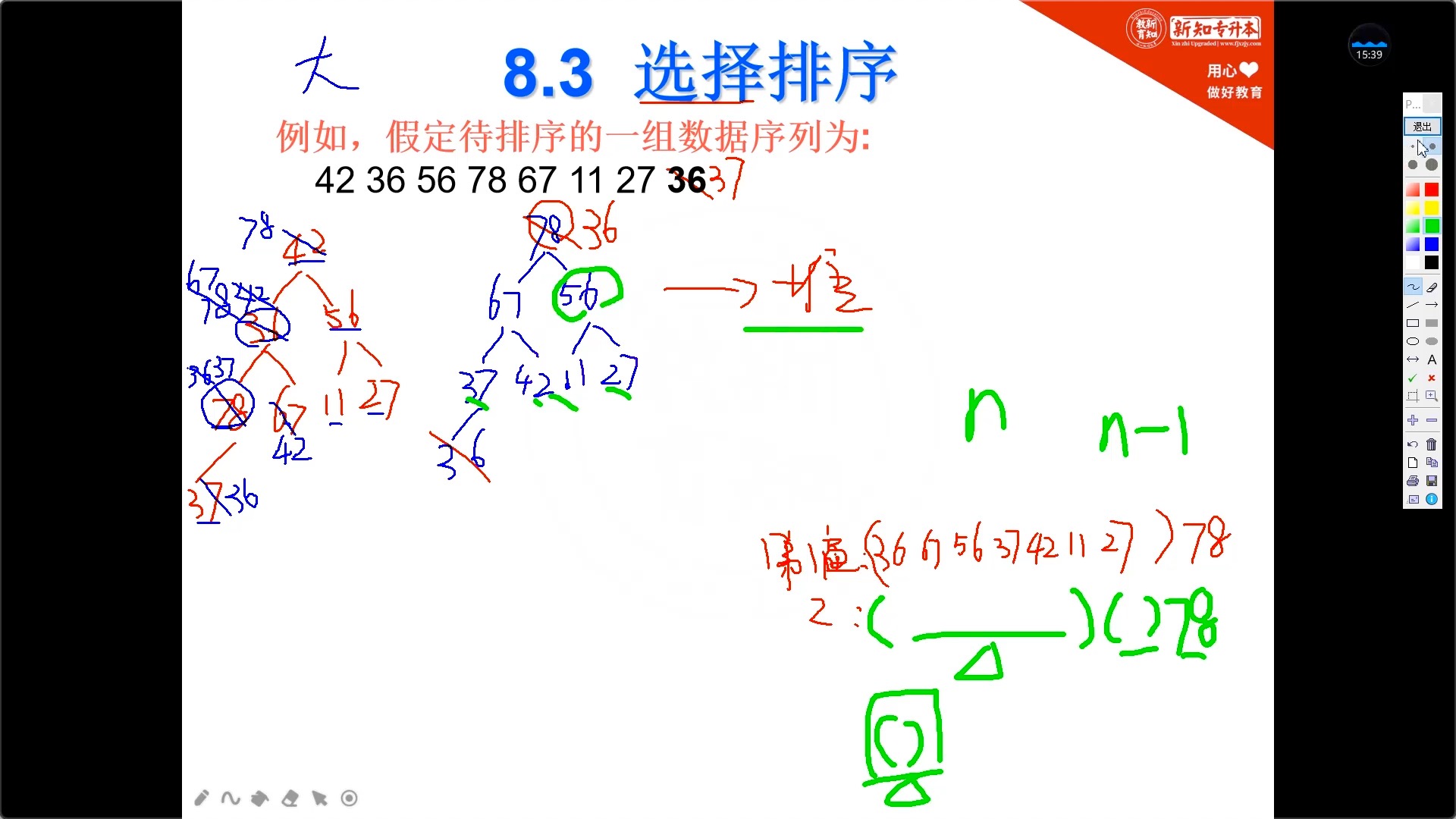
8.4 选择排序 - 堆排序

image-20220221164942070

image-20220221165346514

8.5 交换排序 - 冒泡排序

image-20220221165648430

8.6 交换排序 - 快速排序

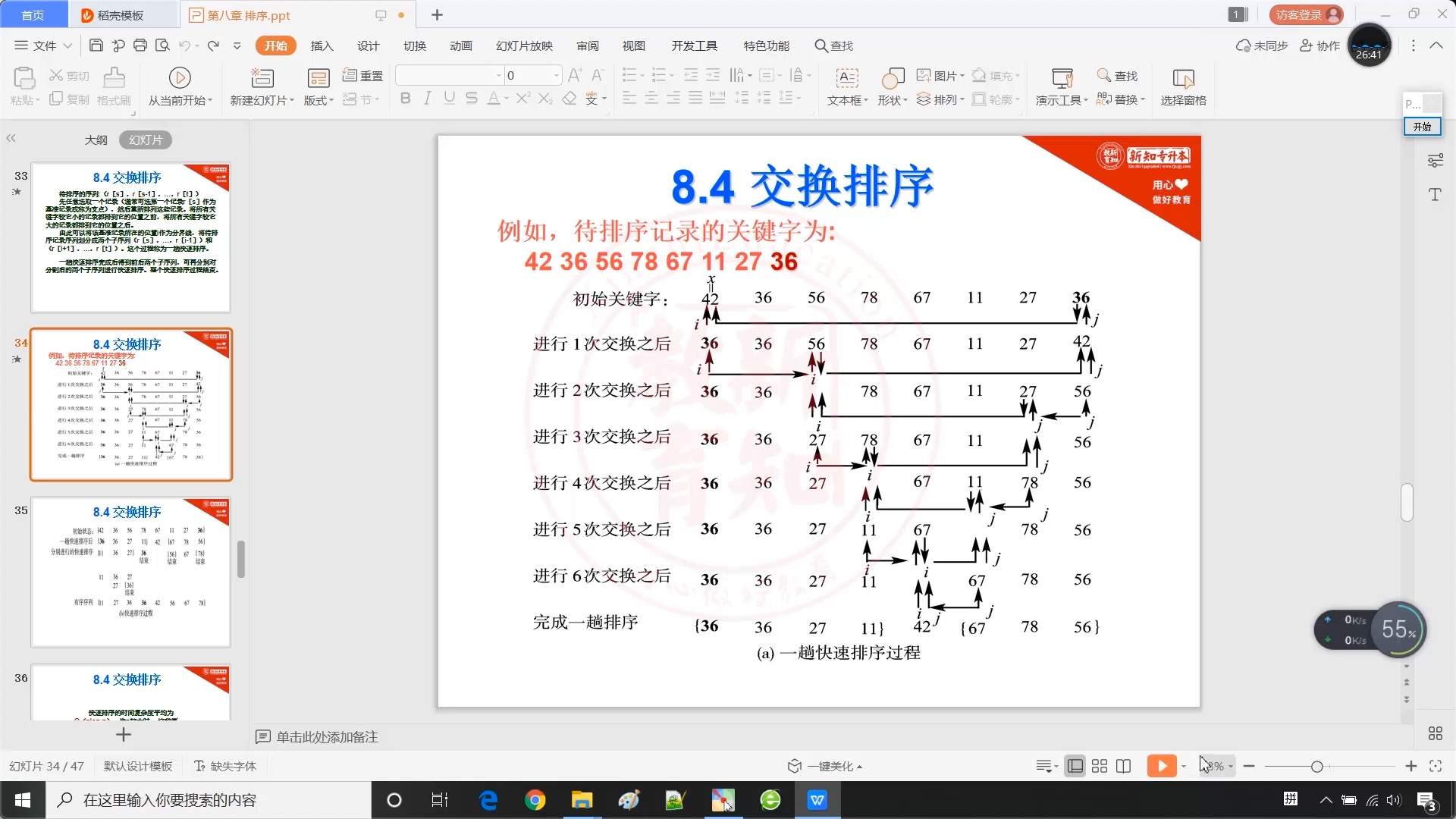
image-20220221170152924

8.7 排序_小结

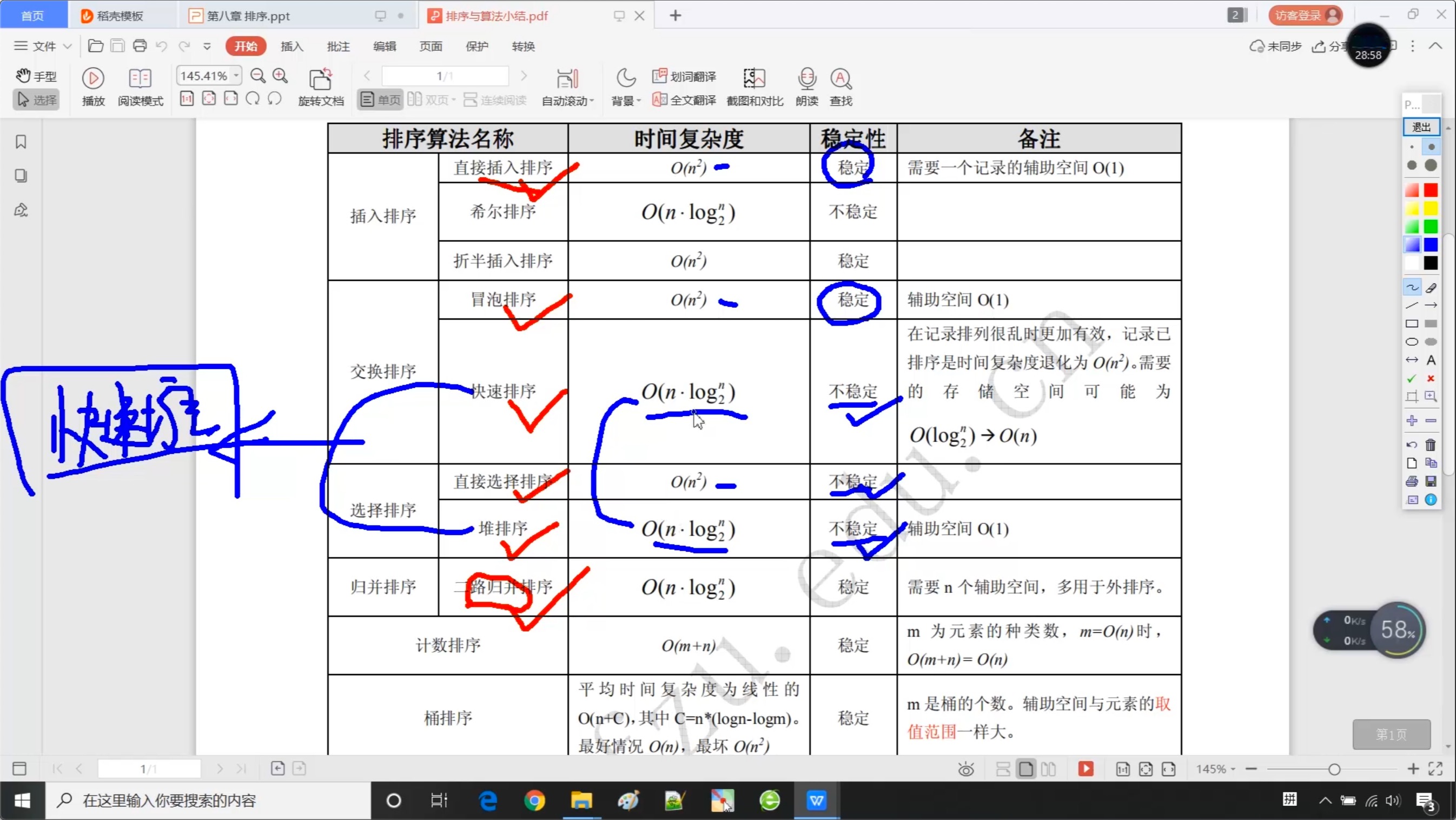
image-20220221170552828

历时三天，完结撒花🌺，这几天每天只学5小时，属实过分了嗷，明天开始要早起！
  数据结构与算法 最新文章
【力扣106】 从中序与后续遍历序列构造二叉
leetcode 322 零钱兑换
哈希的应用：海量数据处理
动态规划|最短Hamilton路径
华为机试_HJ41 称砝码【中等】【menset】【
【C与数据结构】——寒假提高每日练习Day1
基础算法——堆排序
2023王道数据结构线性表--单链表课后习题部
LeetCode 之 反转链表的一部分
【题解】lintcode必刷50题＜有效的括号序列
上一篇文章      下一篇文章      查看所有文章
加:2022-02-22 20:51:10  更:2022-02-22 20:53:10 
 
开发: C++知识库 Java知识库 JavaScript Python PHP知识库 人工智能 区块链 大数据 移动开发 嵌入式 开发工具 数据结构与算法 开发测试 游戏开发 网络协议 系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑 笔记本 显卡 显示器 固态硬盘 硬盘 耳机 手机 iphone vivo oppo 小米 华为 单反 装机 图拉丁

360图书馆 购物 三丰科技 阅读网 日历 万年历 2024年11日历 -2024/11/26 15:32:16-

图片自动播放器
↓图片自动播放器↓ 		TxT小说阅读器
↓语音阅读,小说下载,古典文学↓ 		一键清除垃圾
↓轻轻一点,清除系统垃圾↓ 		图片批量下载器
↓批量下载图片,美女图库↓
  网站联系: qq:121756557 email:121756557@qq.com  IT数码